La media aritmética mediana y la moda en datos agrupados

5/5 - (1 voto)

¿Sabes qué tienen en común la media aritmética, la mediana y la moda con tus redes sociales favoritas o tus videojuegos?

Cada vez que una plataforma te recomienda contenido o un juego analiza tus puntajes, está aplicando medidas de tendencia central. Estas herramientas matemáticas permiten descubrir lo más representativo o típico dentro de un conjunto de datos.

En lugar de revisar cada número uno por uno, la media (promedio), la mediana (valor central) y la moda (valor más frecuente) te ofrecen una visión clara del comportamiento general de la información.

En este post aprenderás cómo calcular estas medidas con datos agrupados y cómo su relación te ayuda a identificar si una distribución es simétrica o sesgada.

Así verás que las matemáticas no solo están en el aula, sino también en el corazón de tu mundo digital, desde las tendencias virales hasta los puntajes récord.

Contenido del tema

Medidas de tendencia central en datos agrupados

Las medidas de tendencia central para datos agrupados (intervalos de clase y frecuencias) son valores estadísticos que representan el punto central o típico de un conjunto de datos, el cual puede corresponder a una población completa o a una muestra representativa de ella.

Al tratarse de datos agrupados el cálculo de estas medidas se realizan mediante fórmulas de estimación, las cuales utilizan las marcas de clase (puntos medios de cada intervalo o clase) y las frecuencias, generando un valor representativo central de los datos.

La media aritmética mediana y la moda

La media aritmética, la mediana y la moda son las tres medidas de tendencia central más utilizadas en estadística. Cada una representa una forma diferente de describir lo que ocurre en un conjunto de datos, permitiendo identificar el comportamiento general o el valor más representativo.

Media aritmética

Es el valor que representa el punto de equilibrio de un conjunto de datos.

En datos agrupados la media aritmética se le denomina media aritmética ponderada, ya que cada clase o intervalo posee una frecuencia específica, y cada frecuencia es una ponderación, es decir, es un peso distinto en cada clase y se calcula como:

$$\bar{x}=\frac{x_{1}\cdot f_{1}+x_{2}\cdot f_{2}+\cdot \cdot \cdot +x_{k}\cdot f_{k}}{f_{1}+f_{2}+\cdot \cdot \cdot +f_{k}}=\frac{\sum_{i=1}^{k}x_{i}\cdot f_{i}}{n}$$

Donde:

x_i= marca de clase.

f_i= frecuencia absoluta.

n = tamaño de la muestra.

Mediana

Es una medida de localización que divide el conjunto de datos en dos partes iguales, determinando el 50% de acumulación de la distribución.

Para hallar la mediana en datos agrupados se aplica la siguiente expresión:

$$M_{e}=L_{i}+\frac{\frac{n}{2}-F_{i-1}}{f_{i}}\cdot a$$

Donde:

M_e= mediana.

n/2 = valor medio del total de los datos.

L_i= límite inferior del intervalo mediano.

F _i-1 = frecuencia absoluta acumulada anterior al intervalo mediano.

f _i = frecuencia absoluta del intervalo mediano.

a = amplitud de los intervalos.

Moda

Es el valor que indica la mayor frecuencia en un conjunto de datos.

Para hallar la moda lo primero es identificar el intervalo modal (intervalo de mayor frecuencia absoluta) y por último aplicar su fórmula que es la siguiente:

$$M_{o}=L_{i}+\frac{r_{1}}{r_{1}+r_{2}}\cdot a$$

M_o= moda.

L_i= límite inferior del intervalo modal.

r₁= es la diferencia de la frecuencia absoluta del intervalo modal y la frecuencia absoluta del intervalo anterior.

$$r_{1}=f_{m}-f_{m-1}$$

r₂= es la diferencia de la frecuencia absoluta del intervalo modal y la frecuencia absoluta del intervalo siguiente al modal.

$$r_{2}=f_{m}-f_{m+1}$$

a = amplitud de los intervalos.

Relación simétrica entre la media aritmética mediana y la moda

La relación simétrica entre la media, mediana y moda revela la forma de la distribución de un conjunto de datos. Su posicionamiento mutuo, ya sea que coincidan o se separen, indica si la distribución es simétrica (equilibrada) o asimétrica (sesgada) al ser graficada en un plano cartesiano.

Se pueden presentar 3 casos ellos son los siguientes:

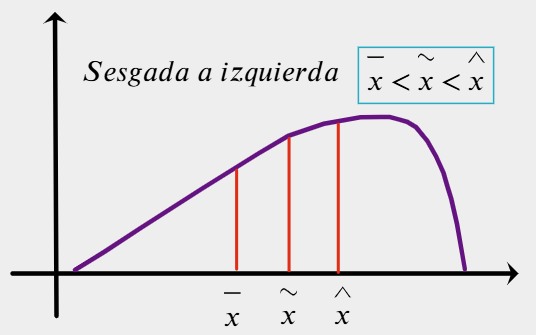
Asimétrica a la izquierda o sesgada a izquierda (sesgo negativo)

La cola de la distribución se extiende hacia la izquierda, indicando algunos valores bajos.
La media aritmética es el valor más inferior, la mediana a la derecha de la media, y el valor más frecuente es la moda ocupando el pico de la distribución.

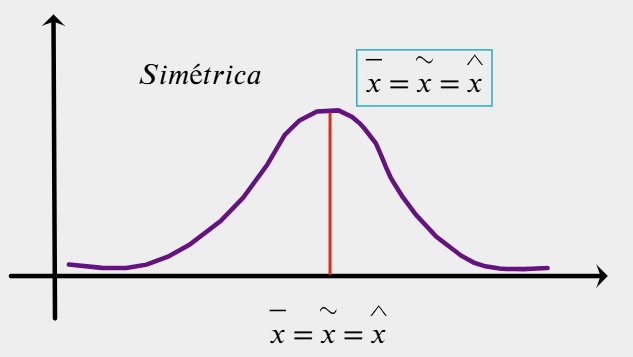
Simétrica (sin sesgo)

Denominada distribución con tendencia normal. Es cuando las tres medidas son iguales, es decir, se genera una distribución perfectamente simétrica.
También puede darse el caso cuando esas tres medidas están muy cercanas entre sí, en este caso la distribución es aproximadamente simétrica.

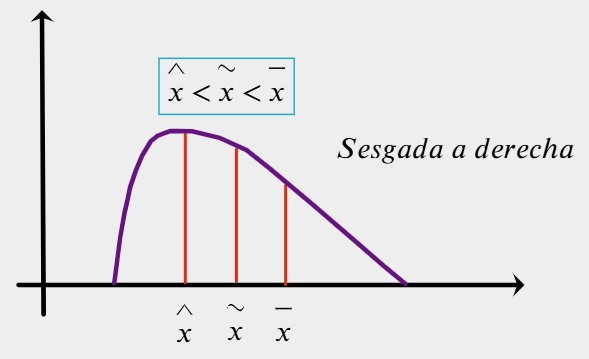
Asimétrica a la derecha o sesgada a derecha (sesgo positivo)

Sucede cuando la media aritmética es valor más alto, la mediana ubicada en la mitad de los datos ordenados y la moda es el valor más frecuente. Ejemplo: Los ingresos anuales de los profesores del colegio Rembrant, su mayoría tienen ingresos modestos o medios, pero hay un pequeño grupo de docentes (Director, administrador, coordinador) con ingresos mucho mayor. ¿Cómo sería el comportamiento de la distribución?

La distribución se comportaría sesgada a la derecha. Lee atentamente la explicación:

La moda, es el valor más frecuente, es decir es el ingreso de la mayoría de los profesores. La mediana, ubicada en la posición central de los datos ordenados. Y la media aritmética expresa los ingresos elevados de los docentes como el director, administrador y el coordinador, aunque sean solo tres docentes, sus ingresos son tan grandes que desplazan el promedio hacia la derecha, mucho más allá de donde se encuentra la mayoría de los profesores.

Ejemplo. Calcular la media aritmética, mediana y moda a partir de una tabla de frecuencias

A continuación, te muestro la información de las velocidades de 80 ciclistas en un Tour de una región europea. Calcular la media aritmética ponderada, mediana la moda y determina la relación de simetría.

Intervalo (km/h)	Marca de clase	Frecuencia (f)	Frecuencia A. (F)	Frecuencia R. (%)
[32 – 36)	34	10	10	12.5%
[36 – 40)	38	18	28	22.5%
[40 – 44)	42	24	52	30.0%
[44 – 48)	46	17	69	21.25%
[48 – 52)	50	11	80	13.75%
Total		80		100%

Solución

Cálculo de la media aritmética ponderada

$$\bar{x}=\frac{\left ( 34\cdot 10 \right )+\left( 38\cdot 18 \right )+\left ( 42\cdot 24 \right )+\left ( 46\cdot 17 \right )+\left ( 50\cdot 11 \right )}{80}$$

$$\bar{x}=\frac{340+684+1008+782+550}{80}=\frac{3364}{80}$$

$$\bar{x}=42,05 \frac{km}{h}$$

Cálculo de la mediana

Reemplazar el límite inferior del intervalo mediano y el valor medio del total de los datos:

$$M_{e}= 40+\frac{\left ( 40-28 \right )}{24}\cdot 4$$

Operar aritméticamente:

$$M_{e}= 40+\frac{\left ( 12 \right )}{24}\cdot 4$$

Sumar

$$M_{e}= 40+2$$

La mediana de la velocidad es:

$$M_{e}= 42 \frac{km}{h}$$

Cálculo de la moda

$$r_{1}=24-18$$

$$r_{1}=6$$

$$r_{2}=24-17$$

$$r_{2}=7$$

$$M_{o}=40+\left ( \frac{6}{6+7} \right )\cdot 4$$

$$M_{o}=40+\frac{24}{13}$$

$$M_{o}=\frac{544}{13}$$

$$M_{o}\approx 41,85 \frac{km}{h}$$

Resumen:

$$\bar{x}=42,05 \frac{km}{h}$$

$$M_{e}=42 \frac{km}{h}$$

$$M_{o}\approx 41,85 \frac{km}{h}$$

Conclusión:

Las tres medidas son muy cercanas entre sí, lo cual indica una distribución relativamente simétrica de los datos. Por tanto es una distribución aproximadamente simétrica.

Diagnóstico: Media, Mediana, Moda y Tipos de Sesgo

Reflexiona y responde estas preguntas. Luego haz clic en “Ver respuesta correcta” para comparar con tu razonamiento.

1. ¿Qué representa la media aritmética en un conjunto de datos agrupados?

🔸 El valor más frecuente del conjunto.
🔸 El valor central que divide los datos en dos partes iguales.
🔸 El promedio de todos los datos considerando sus frecuencias.

Ver respuesta correcta

✅ La media representa el promedio ponderado de los datos agrupados.
Se obtiene multiplicando la marca de clase por la frecuencia de cada intervalo y dividiendo entre el total de datos.

2. ¿Qué ocurre en una distribución simétrica sin sesgo?

🔸 La moda es mayor que la media.
🔸 La media es menor que la mediana.
🔸 Media, mediana y moda coinciden o son muy similares.

Ver respuesta correcta

✅ En una distribución simétrica, los datos se distribuyen de forma equilibrada:
media = mediana = moda.
Esto indica que no existe inclinación hacia ningún extremo.

3. En una distribución con sesgo positivo, los valores tienden a concentrarse hacia:

🔸 Los valores altos, con una cola extendida hacia la izquierda.
🔸 El centro, sin inclinación visible.
🔸 Los valores bajos, con una cola extendida hacia la derecha.

Ver respuesta correcta

✅ En un sesgo positivo, la mayoría de los datos se concentran en los valores pequeños,
y la cola se extiende hacia la derecha.
La media es mayor que la mediana en este tipo de distribución.

💡 Reflexiona: Si logras relacionar la media, mediana y moda con el tipo de sesgo,
estás listo para analizar distribuciones estadísticas con confianza.

¿Quieres practicar más con un tutor?

Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.

Solicita una tutoría

Actividades

Representa gráficamente la relación simétrica de las siguientes medidas de tendencia central.

$$M_{o}=2,785;\bar{x}=5,981;M_{e}=3,478$$

$$M_{o}=2,1510;\bar{x}=2,1500; M_{e}=2,1505$$

$$M_{o}=159,0501;\bar{x}=159,0501;M_{e}= 159,0501$$

Resuelve el siguiente problema.

En un salón de clases de 9° grado se registraron las estaturas (en centímetros) de 40 estudiantes con el propósito de analizar cómo se distribuyen y varían dentro del grupo. A partir de estos datos, debes caracterizar las estaturas utilizando medidas de tendencia central (media, mediana y moda), así como representar gráficamente la distribución para obtener una visión general del comportamiento de este conjunto de datos.

143 cm	150 cm	162 cm	169 cm	174 cm	182 cm	158 cm	166 cm
145 cm	153 cm	160 cm	170 cm	176 cm	185 cm	151 cm	164 cm
147 cm	157 cm	165 cm	168 cm	172 cm	184 cm	149 cm	161 cm
148 cm	159 cm	163 cm	167 cm	171 cm	181 cm	152 cm	160 cm
144 cm	156 cm	164 cm	166 cm	175 cm	186 cm	150 cm	162 cm

Construye la distribución de frecuencias.
Determina las medidas de tendencia central de la distribución de frecuencias e interpreta.
Diga la relación de simetría que tiene la distribución de frecuencias e interpreta los resultados.

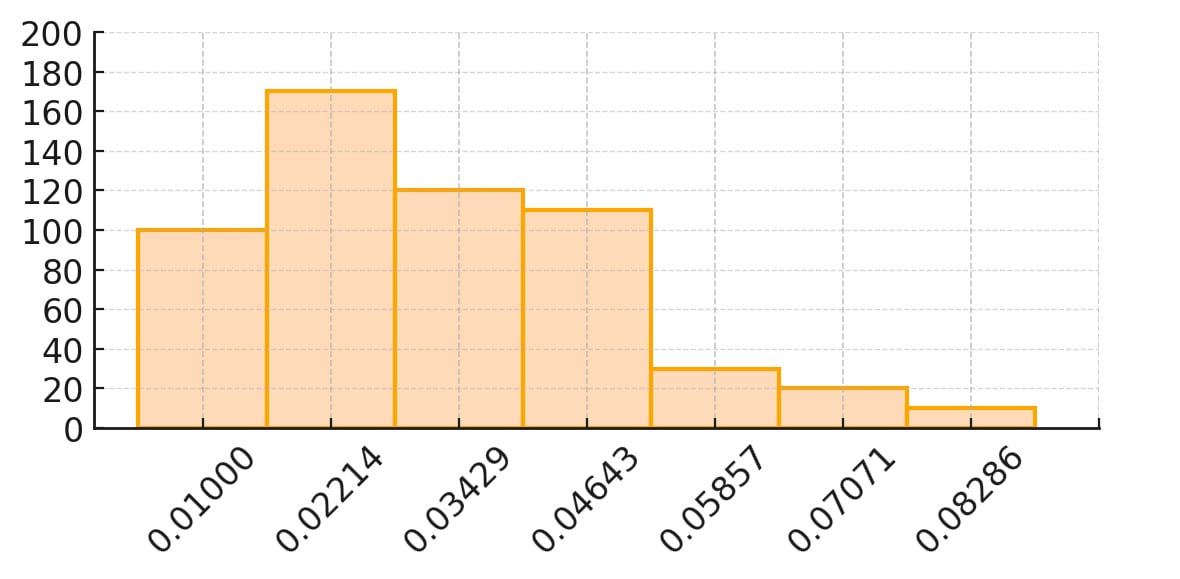
Identifica la relación simétrica del siguiente histograma