¿Alguna vez te has preguntado cómo las medidas de dispersión revelan lo que las cifras promedio esconden? Piensa en tu videojuego favorito: tu puntaje medio es de 5000 puntos por partida, pero eso no dice si juegas siempre igual o si un día haces 1000 y al siguiente rompes récords con 9000.
Ahí está la magia de estas medidas: muestran qué tan consistentes o variables son tus resultados. Una desviación estándar baja indica estabilidad; una alta, altibajos marcados. Entenderlas te permite ir más allá del promedio y descubrir la verdadera historia detrás de los datos, ya sea en el deporte, el estudio o tus redes sociales.
Medidas de Dispersión
| Conocida también como medidas de variabilidad, su función es medir cuánto se dispersan o alejan los valores observados (los datos) de la unidad de observación respecto a las medidas de tendencia central (valores centrales) de la distribución. |
Conceptos clave del análisis de dispersión
Antes de profundizar en el tema, es fundamental dominar ciertos conceptos. A continuación, se detallan las terminologías esenciales:
Unidad de observación (o individuo)
Es el elemento básico sobre el cual se realiza una medición. Ejemplo: En el Colegio Marimar, cada estudiante individual de 9° grado representa una unidad de observación.
Observación
Es el dato o el valor específico obtenido de cada elemento del estudio. Ejemplo: La nota de Juan en el examen final de matemáticas fue de 8,5 puntos.
Población
Es el total de todos los individuos que comparten una característica en común. Ejemplo: El total de estudiantes de 9° grado del Colegio Marimar.
Muestra
Es una parte representativa seleccionada de una población. Es aplicado cuando es inviable la recopilación de datos en cada elemento de la población, ya sea por costos, consumo de mucho tiempo, situaciones imposibles en la práctica como contactar a todos los niños de 7 años de un país.
Los resultados de una muestra son usados para inferir sobre la población de la cual fue extraída.
Ejemplo: Como existe dificultad para evaluar a todos los estudiantes de 9° grado de un municipio, la Secretaría de Educación selecciona a 200 estudiantes de distintos colegios para aplicarles el examen de matemáticas. Esos 200 estudiantes pertenecen a la muestra.
Tipos de medidas de dispersión
Existen varios tipos de medidas de dispersión, como el rango, desviación media absoluta, varianza y la desviación estándar.
El rango
Es la medida de dispersión más sencilla y se calcula mediante la fórmula:
$$ R=V_{M}-V_{m}$$
Ejemplo: En un salón, la nota más alta es 10 y la más baja es 3. El rango de esta situación es:
$$ R=10-3=7$$
Los 7 puntos expresa la extensión total de las notas, da una idea pero no dice cómo están las notas entre 3 y 10.
Desviación media absoluta
Es una medida de dispersión que mide el promedio de las distancias que cada valor observado tiene respecto al valor promedio de todo el conjunto de datos. Se calcula por medio de la siguiente expresión:
Para datos no agrupados
$$DMA=\frac{\sum_{i=1}^n{\left | \bar{x}-x_{i}\right |}}{n}$$
Donde:
DMA = Desviación Media Absoluta.
xi = Valor individual del conjunto de datos.
= Media aritmética
n =Total de datos del conjunto:
Datos agrupados
$$DMA=\frac{\sum_{i=1}^kf_{i}\cdot {\left | \bar{x}-x_{i}\right |}}{n}$$
Donde:
fi = Frecuencia absoluta de cada clase.
xi = Marca de clase.
n = Número total de observaciones.
Ejemplo. Determinar la Desviación Media Absoluta en la siguiente situación
Un grupo de estudiantes de 9° grado ingresaron al servicio médico y el Dr. Emilio midió la altura de cada uno ellos. Los resultados fueron los siguientes:
Aníbal 1,70m; Katerine 1,60m; David 1,75m; Mara 1,65m; Daniel 1,80m.
Solución
El promedio de la alturas es:
$$\bar{x}=1,70m$$
Para determinar la DMA se calcula el valor absoluto de la diferencia de la altura del estudiante y la media aritmética, de esta forma se conoce cuánto se aleja la altura de uno de ellos con respecto a la media aritmética.
Aníbal = |1,70m – 1,70m| = 0
Katerine = |1,60m – 1,70m| = 0,10m
David = |1,75m – 1,70m| = 0,05m
Mara = |1,65m – 1,70m| = 0,05m
Daniel = |1,80m – 1,70m| = 0,10m
¿Qué quiere decir esto?
Significa que Daniel se aleja de la media a un 0,10m, José a 0,05m, David 0,05, Pepe 0,10m y Anibal ningún alejamiento.
Posteriormente, la DMA toma el promedio de todos los valores absolutos individuales a la media:
DMA =(0 + 0,10m + 0,05m + 0,05m + 0,10m )/5 = 0,06m.
¿Qué significa que DMA = 0,06m?
Significa que, en promedio, la altura de cada estudiante se desvía 0,06m con respecto a la altura promedio del grupo de 9° grado.
Varianza
Es una medida de dispersión que tiene como finalidad expresar qué tan alejados están los valores de un conjunto de datos respecto a su media aritmética.
La varianza usa todos los datos basándose en la diferencia que existe entre el valor de cada uno de ellos y la media aritmética del conjunto, esa diferencia se le conoce como desviación de un dato respecto al promedio (media aritmética).
¿Cómo se representa?
Para calcular la varianza en una muestra se representa como s2 y si es en una población, se utiliza σ2 .
¿Cuál es su fórmula?
Para una muestra se calcula por medio de la siguiente expresión:
$$s^{2}=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}{n-1}$$
Donde:
Desviación del dato i con respecto a la media:
$$(x_{i}-\bar{x})$$
Número de datos: n
En una población, se emplea la siguiente expresión:
$$\sigma^{2}=\frac{\sum_{i=1}^{n}(x_{i}-\mu )^{2}}{N}$$
Donde:
σ = Media poblacional.
N = Tamaño de la población.
Ejemplo. Calcule la varianza
En un colegio un profesor de física se interesó en conocer la variabilidad en el rendimiento académico de sus estudiantes en la evaluación final, debido a la gran cantidad de alumnos decide seleccionar al azar una muestra representativa de 5 estudiantes para un análisis más detallado. Las notas obtenidas fueron las siguientes: 7, 8, 6, 9, 5.
Solución
El promedio de notas es: $$\bar{x}=7$$
$$s^{2}=\frac{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+(x_{3}-\bar{x})^{2}+(x_{4}-\bar{x})^{2}+(x_{5}-\bar{x})^{2}}{n-1}$$
$$s^{2}=\frac{(7-7)^{2}+(8-7))^{2}+(6-7)^{2}+(9-7)^{2}+(5-7)^{2}}{5-1}$$
$$s^{2}=\frac{10}{4}=2,5$$
La varianza de las notas es 2,5 indicando que las notas están relativamente agrupadas alrededor de la media (7).
Desviación estándar
Llamada también desviación típica definida como la raíz cuadrada de la varianza.
Para una muestra se define como:
$$s=\sqrt{s^{2}}=\sqrt{\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}{n-1}}$$
Para una población:
$$\sigma =\sqrt{\sigma ^{2}}=\sqrt{\frac{\sum_{i=1}^{n}(x_{i}-\mu )^{2}}{N}}$$
¿Qué significado tiene?
Con un resultado reducido indica que existe poca variabilidad en la muestra de datos analizados, por tanto las observaciones tienen una mayor tendencia de agruparse alrededor de la media.
Con un resultado alto revela una mayor dispersión, esto quiere decir que las observaciones se encuentran más alejadas de la media aritmética.
Ejemplo. Hallar la desviación estándar
En la situación mostrada anteriormente la varianza fue de 2,5 indicando una relativa tendencia al promedio. En este caso se pide determinar la desviación estándar
$$s=\sqrt{2,5}\approx 1,58$$
Esto significa que, en promedio, las notas de los estudiantes se desvían alrededor de 1,58 puntos del promedio de 7. Es un valor relativamente pequeño para el rango de notas (0 a 10) expresando que las notas en la muestra están muy agrupadas respecto a la media aritmética (promedio).
Ejemplo práctico explicado paso a paso
Se realiza una encuesta a 65 empleados de una empresa de telecomunicaciones sobre el tiempo (min) que tardan en su trayecto diario de casa al trabajo. Determinar:
- Rango,
- La desviación media aritmética,
- Varianza y
- La desviación estándar.
Tiempo (minutos) que tardan cada empleado:
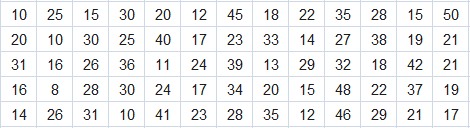
Solución
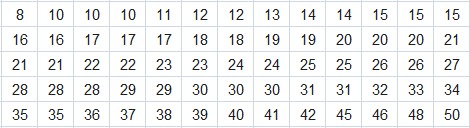
Uno: Ordenar de forma ascendente el tiempo.
Dos: Crear la tabla de frecuencias por intervalos.
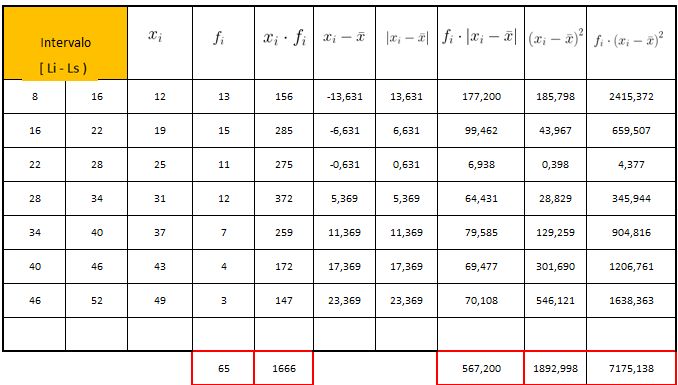
Tres: Cálculo de las Medidas de Dispersión.
- Media aritmética
$$\bar{x}=\frac{\sum_{i=1}^{k}x_{i}\cdot f_{i}}{n}=\frac{1666}{65}\approx 25,6\, min$$
- Rango
$$ R=V_{M}-V_{m}$$
$$ R=50-8=42min$$
- Desviación media absoluta
$$DMA=\frac{\sum_{i=1}^kf_{i}\cdot {\left | \bar{x}-x_{i}\right |}}{n}$$
$$DMA=\frac{\sum_{i=1}^kf_{i}\cdot {\left | \bar{x}-x_{i}\right |}}{n}=\frac{567,2}{65}\approx 8,7\, min$$
- Varianza
$$\sigma^{2}=\frac{\sum_{i=1}^{n}(x_{i}-\mu )^{2}}{N}=\frac{7175,138}{65}\approx 110,4\, min^{2}$$
- Desviación estándar
$$\sigma =\sqrt{\sigma ^{2}}=\sqrt{110,4\, min^{2}}\approx 10,5\, min$$
Significado de las medidas de dispersión
Los resultados de las medidas de dispersión ofrecen una imagen clara de la variabilidad en sus trayectos:
Rango (R=42 minutos):
La diferencia entre el tiempo que más tarda en llegar (50min) y el que menos tarda (8min) es considerable ya que su amplitud es de 42 minutos, ese rango ya apunta que existe una variabilidad significativa en los tiempos de desplazamiento.
Desviación Media Absoluta (DMA≈8,7 minutos):
En promedio, los tiempos de viaje de cada empleado se desvían alrededor de 8,7 minutos respecto a la media de 43 minutos.
Varianza (σ2 ≈110,4 min2):
Su valor confirma la existencia de una dispersión en los datos.
Desviación Estándar (σ ≈ 10,5 min):
Un valor de 10,5 minutos indica que, en promedio, los tiempos de viaje de los empleados se separan 10,5 minutos de la media de 25,6 minutos.
Conclusión
La desviación estándar de 10,5 minutos es relativamente alta en comparación con el promedio del tiempo de 43 minutos ya que representa un 41% de la media. Esto quiere decir que existe una gran dispersión en los tiempos individuales.
Entonces, no todos los trabajadores tardan un tiempo similar en llegar al trabajo, un grupo significativo de empleados llegan mucho más rápido y otro grupo tardan considerablemente más que el promedio.
Para la empresa, esa alta variabilidad puede implicar desafíos en la planificación de horarios o incluso la necesidad de explorar opciones de transporte para sus empleados dado que los tiempos de desplazamientos no son consistentes entre ellos.
Actividades de las medidas de dispersión
Resuelve las siguientes situaciones
Se registran las temperaturas máximas diarias en un poblado durante un período de 32 días consecutivos en la estación seca.
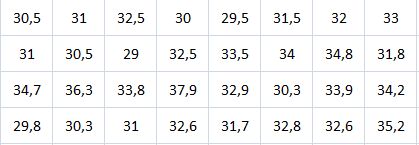
- Construye la tabla de distribución de frecuencias.
- ¿Cuál es la media de las temperaturas?
- ¿Cuál es la desviación media absoluta de las temperaturas? Interprete.
- Existe una variabilidad considerablemente grande entre los datos recogidos.
- ¿Cuánto es la desviación estándar? Interprete.
Haz un resumen de las conclusiones fundamentales que surgen de estas experiencias de aprendizaje.
- ¿La desviación estándar puede tomar valores negativos? Justifica.
- ¿Es posible que la desviación estándar sea igual a cero?
- Identifica qué tipo de variable estadística permite el cálculo de la desviación estándar.
Dada las siguientes afirmaciones selecciona Verdadero o Falso
1.La Varianza puede tomar valores negativos.
- Verdadero.
- Falso.
2.La desviación estándar se expresa en las mismas unidades que los datos originales.
- Verdadero.
- Falso.
3.El rango es una medida de dispersión muy resistente a los valores atípicos (outliers).
- Falso.
- Verdadero.
4.La Desviación Media Absoluta (DMA) es matemáticamente más fácil de usar en inferencia estadística avanzada que la varianza o la desviación estándar.
- Verdadero.
- Falso.
5.Si todas las observaciones en un conjunto de datos son idénticas, su desviación estándar es cero.
- Falso.
- Verdadero.
Comparte esto:
Descubre más desde LaProfematematiK "Dios es Bueno"
Suscríbete y recibe las últimas entradas en tu correo electrónico.