¿Quieres saber más de aproximación numérica? ¿Alguna vez has notado que, al dividir, tu calculadora a veces «corta» los números? O, ¿has visto que al comprar alguna cosa, los precios no siempre son exactos hasta el último decimal? ¡Pues no es magia! Detrás de esas situaciones cotidianas se esconden dos trucos matemáticos que usamos sin darnos cuenta todo el tiempo: el redondeo y el truncamiento.
En este post, entenderás cómo funciona el redondeo y el truncamiento. Además, aprenderás a calcular el error, esa pequeña diferencia que existe entre un número «perfecto» y su versión «aproximada».
¿Qué es una aproximación por redondeo?
| Es adicionar uno a la cifra significativa (a la décima, a la centésima, a la milésima, a diezmilésima, etc.) si el dígito de la derecha es mayor o igual a 5, si no es así se deja igual. |
Su procedimiento es el siguiente:
- Identificar la cifra significativa.
- Calcular el valor numérico solo si la expresión dada es radical o fracción.
- Verificar el dígito de la derecha (de la cifra significativa). Sí este es:
Dígito > 5 se le suma 1 a la cifra significativa.
Dígito < 5 se deja igual la cifra significativa.
Ejemplos de redondeo
Aproximar por redondeo las siguientes expresiones a la centésima y a la milésima: $$\sqrt{5}\,\,y\,\,\frac{1}{3}$$
Ejemplo # 1
| $$\sqrt{5}$$ | ||
| 1° | A la centésima | |
| 2° | $$\sqrt{5}=2,236067$$ Se escribe la cifra significativa y el número de la derecha: 2,236 | |
| 3° | El dígito a la derecha de la centésima es > 5 | Respuesta: (+1) 2,24 |
| 1° | A la milésima | |
| 2° | $$\sqrt{5}=2,2360$$ | |
| 3° | A la derecha de la milésima es < 5 | Respuesta: ( = ) 2,236 |
Ejemplo # 2
| $$\frac{5}{6}$$ | ||
| 1° | A la centésima | |
| 2° | $$\frac{5}{6}=0,83333…$$ 0,833 | |
| 3° | Es < 5 | Respuesta: ( = ) 0,83 |
| 1° | A la milésima | |
| 2° | 0,8333 | |
| 3° | A la derecha de la milésima es < 5 | Respuesta: ( = ) 0,833 |
Aproximación por truncamiento
Se trata de acortar un número decimal eliminando los dígitos que están después de la cifra significativa sin aplicar el redondeo.
Ejemplo # 1. Aproximar por truncamiento 0,567 a la centésima.
Respuesta: 0,56.
Ejemplo # 2. Busca un número que al redondearlo y truncarlo a las décimas dé el mismo resultado.
Existen muchos números que cumplen esa condición, uno de esos números es 3,141 ya que al redondearlo queda 3,1 y al truncarlo también se obtiene 3,1.
Errores en las aproximaciones
Cada vez que se realiza una aproximación, se genera un error con respecto al valor real del número. Este error indica qué tanto se aleja la aproximación del valor exacto. Existen dos tipos de errores:
- Error absoluto (Ea): Es el valor absoluto de la diferencia del valor real y el valor aproximado. Este error muestra la distancia entre dichos valores.
- Error relativo (Er): Es el valor absoluto de la división del error absoluto entre el valor real. Este tipo de error indica el porcentaje.
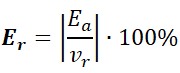
Aplicaciones y ejemplos prácticos
Las aproximaciones por redondeo se usan con frecuencia en situaciones cotidianas donde no es necesario conocer un valor exacto, como estimar precios, tiempos o medidas. Comprender cómo aplicar el redondeo y reconocer el error que genera es clave para tomar decisiones razonables en contextos reales.
A continuación, aquí tienes algunos ejemplos:
Problema 1:
Camila es chef en un restaurante y preparó 48 empanadas en 65 minutos. ¿Aproximadamente cuántos minutos tardó en preparar cada empanada? Redondea al número entero más cercano y determine el error de la aproximación.
Solución:
Se divide los 65 ÷ 48 = 1,354166666…
Aproximando por redondeo al entero 1,354166666… ≈ 1
Camila tardó 1min en hacer cada empanada.
Por tanto,
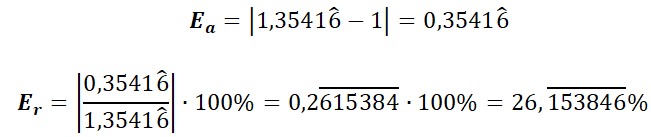
Problema 2:
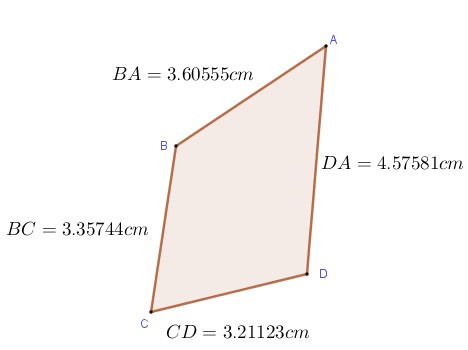
Determinar el perímetro del cuadrilátero ABCD, si se redondean a las centésimas y hallar el error de la aproximación de este valor.
Solución:
Lo primero, es aproximar por redondeo cada lado del cuadrilátero.
Calculo del perímetro:
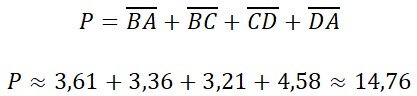
El perímetro aproximado por redondeo a las centésimas es 14,76cm.
Por último, se calcula el error de la aproximación. Para esto se halla el perímetro sin aproximar cada longitud del cuadrilátero.
Por tanto,
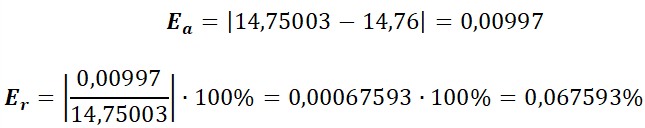
¿Cifras exactas o aproximadas? ¡Descúbrelo con nuestra simulación de redondeo y truncamiento!
¿Alguna vez te has preguntado cómo los científicos, ingenieros o incluso tu mamá con el presupuesto familiar manejan esos números larguísimos con muchísimos decimales? ¡No siempre los usan todos! Para hacer las cosas más prácticas, usan dos técnicas increíbles: el truncamiento y el redondeo.
En esta simulación interactiva, vas a ser el experto en números. Podrás tomar cualquier número decimal y ver con tus propios ojos cómo cambia cuando lo “cortas” (truncas) o lo “ajustas” (redondeas) a diferentes partes: unidades, décimas, centésimas o milésimas. ¿Notarás la diferencia? ¿Cuál crees que es más preciso? ¡Es hora de dejar de imaginar y empezar a experimentar! ¡Presiona el botón (otro) para cambiar el número y luego prueba las opciones de truncamiento y redondeo!
¡Queremos saber tu opinión!
¿Qué te pareció la simulación? ¿Lograste ver claramente la diferencia entre truncar y redondear un número? ¿Cuál te parece más útil en la vida diaria? ¡Comparte tus observaciones y dudas en los comentarios al final de este post! Tu experiencia nos ayuda a mejorar y a entender mejor cómo ves este fascinante mundo de los números aproximados. ¡Anímate a comentar!
Actividades
1.Redondea para determinar una aproximación a la cifra significativa señalada.
| A las décimas | A las milésimas | ||
| a) | 135,2730425 | c) | $$3+\sqrt{2}$$ |
| b) | 9 089,409098 | d) | $$2,\widehat{9}$$ |
2.Aplica el truncamiento para determinar una aproximación a la cifra significativa señalada.
| A las milésimas | A las centésimas | ||
| a) | $$5+\sqrt{7}$$ | a) | 0,128875 |
| b) | 5,01257… | b) | 4,01012 |
| c) | $$\sqrt{11}$$ | c) | $$\sqrt{2}+\sqrt{13}$$ |
| d) | $$51,4\widehat{3}$$ | d) | $$8,\widehat{8}$$ |
3.Soluciona cada operación por redondeo y por truncamiento a las centésimas. Luego compara los resultados y establece el error de aproximación.
| a) | 5,8875+6,3186 | c) | $$\sqrt{15}+\sqrt{2}+\pi$$ |
| b) | 8,034+π | d) | $$8,\widehat{8}+2,\widehat{1}$$ |
4.Observa el siguiente polígono y determina:
a. La diagonal aproximada por truncamiento y por redondeo a la décima.
b. El error de aproximación por truncamiento y por redondeo.
Comparte esto:
Descubre más desde LaProfematematiK "Dios es Bueno"
Suscríbete y recibe las últimas entradas en tu correo electrónico.