¿Sabes cómo calcular el área usando cuadros? ¿Te imaginas que calcular el área sea tan fácil como contar cuadritos? En este post vas a aprender a calcular el área de una figura usando cuadrículas. Cada cuadrito representa un valor en unidades cuadradas, y lo único que debes hacer es contar cuántos cuadros ocupa la figura. Así descubrirás, de forma visual y divertida, cómo se suma el área total, es como armar un mapa: ¡cuantos más cuadros sumes, mayor será el área!
¿Qué es el área?
Es una magnitud que permite medir la superficie de una figura plana. Su unidad es derivada de la longitud elevada al cuadrado, ya que el área mide superficies en dos dimensiones. Algunas unidades en el sistema métrico decimal son: m2, cm2, km2 y mm2.
Entender qué es el área, es como agregar triangulitos dentro de otro triángulo de mayor tamaño, al llenarlo se cuenta el total de ellos, obteniendo así el área del triángulo mayor. Observa el siguiente triángulo:
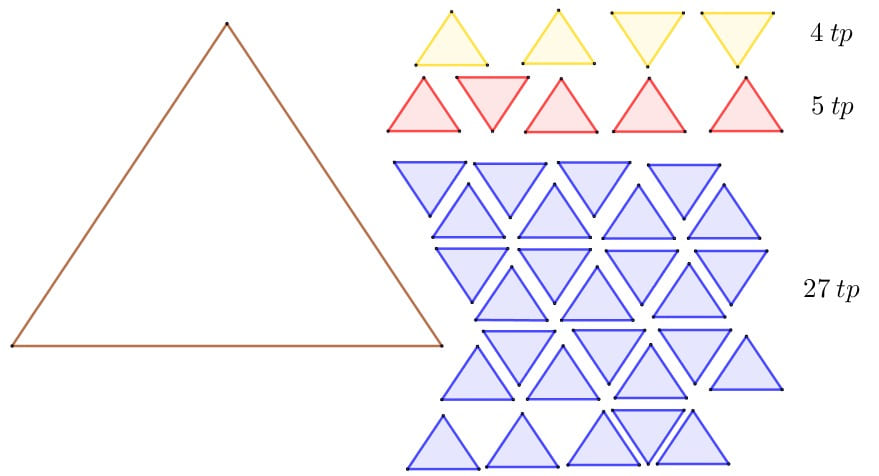
Aquí se agregaron todos los triangulitos, cuéntalos el área es de 36 tp.
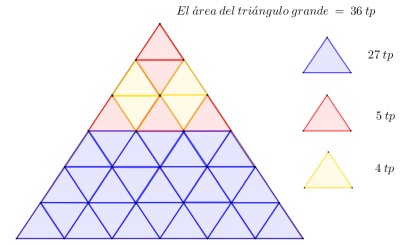
Determinar el área de cada figura
En esta parte aprenderás a calcular el área total de una figura plana contando los cuadros de una cuadrícula, donde cada uno representa 1 unidad cuadrada (1 u²). También conocerás cómo obtener el área de una región sombreada restando las áreas vacías.
Parte I: Sumando el total de cuadrículas
Observa con atención cada paso para calcular fácilmente el área de cada figura.
Ejemplo # 1. Obtener el área total, cada cuadrícula tiene un valor de 1u2.
Paso 1. Identificar las cantidades de cuadrículas involucradas, ellas son:
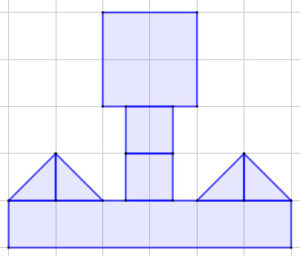
12 Cuadrados (cuadrículas) y
4 Triángulos (2 cuadrículas).
Paso 2. El área es:
AT = 12u2 + 2u2 = 14u2
AT = 14u2
Ejemplo # 2. Calcular el total, compuesta por 3 áreas sombreadas.
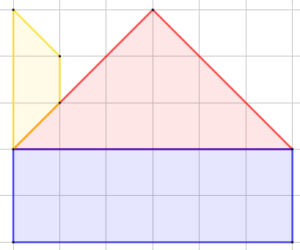
Azul: 12u2
Roja: 9u2
Amarilla: 2u2
AT = 12u2 + 9u2 + 2u2 = 23u2
AT = 23 u2
Parte II: Sumando específicamente las cuadrículas
Para este caso la figura está compuesta por un área sombreada y otra en blanco. El área sombreada es el área total y la superficie blanca es el área vacía. Para obtener el valor del área total debes contar solo el área sombreada.
Ejemplo # 1: La figura a continuación está compuesta por dos rectángulos. Un rectángulo mayor y otro menor.
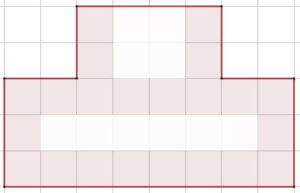
El área total del rectángulo mayor es:
Rectángulo mayor = 18u2
La superficie del rectángulo menor:
Rectángulo menor = 4u2
Área total de la figura = 18u2 + 4u2 = 22u2
Área total de la figura = 22u2
Ejemplo # 2: Determinar el área total sombreada.
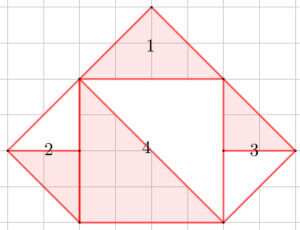
Análisis: La figura está compuesta por cuatro figuras planas, los tres triángulos son de la misma forma y del mismo tamaño, por lo tanto sus áreas son las mismas.
Áreas de cada figura:
1 Triángulo = 4u2
Cuadrado = 16u2
3 Triángulos = 3.4u2=12u2
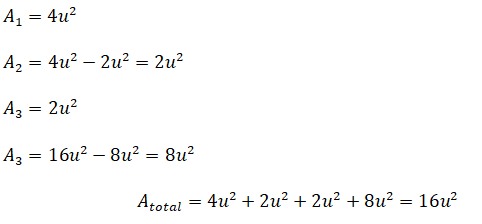
A jugar construyendo áreas
Ahora que ya conoces el tema, llegó el momento de jugar y profundizar tus conocimientos con esta interesante simulación.
Explora esta divertida simulación y sigue aprendiendo mientras construyes y descubres áreas de diferentes figuras.
Te invitamos a dejar tu comentario abajo. Cuéntanos qué aprendiste, qué te gustó más o si te surgió alguna duda. ¡Tu opinión es muy importante para nosotros!.
Actividades
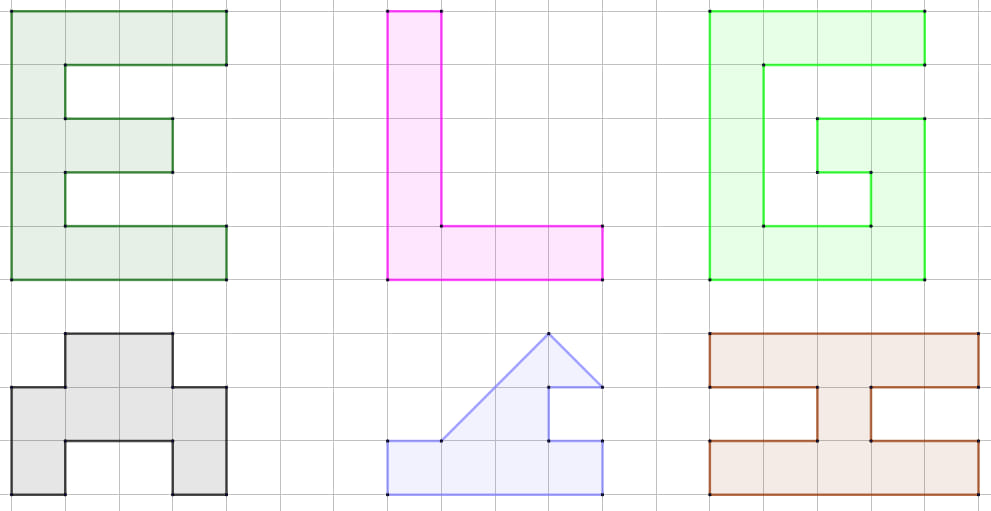
I. Calcula el área de cada figura. Utiliza el cuadrado de la cuadrícula como unidad de medida.
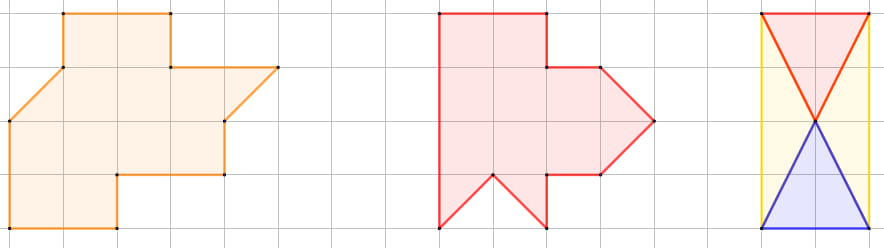
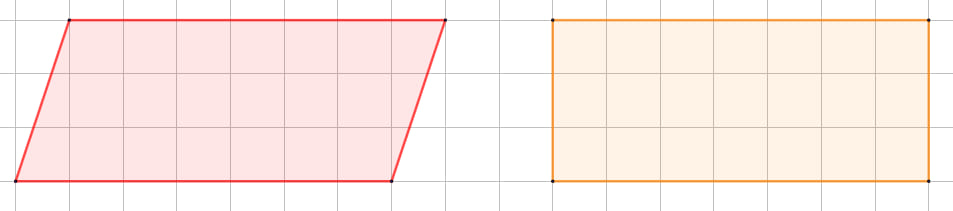
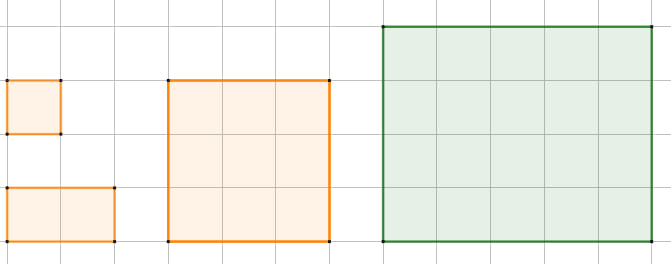
II. Las figuras a continuación, ¿poseen las mismas áreas?
III. Determina la diferencia de las dos áreas sombreadas, sabiendo que el valor de la cuadrícula es de 2u2.
IV. Calcular el área sombreada de la siguiente figura. Cada cuadrícula es de 10u2
Comparte esto:
Descubre más desde LaProfematematiK "Dios es Bueno"
Suscríbete y recibe las últimas entradas en tu correo electrónico.