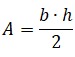¿Estás buscando cómo calcular el área de cuadriláteros, triángulos, polígonos regulares y círculos? Si es así, has llegado al lugar indicado. ¿Sabías que calcular áreas no es solo cosa de matemáticas en clase? Cuando juegas fútbol, el campo tiene forma de rectángulo (¡un cuadrilátero!), en los videojuegos los mapas y zonas seguras tienen formas geométricas, y hasta los íconos que usas en redes sociales pueden ser círculos o polígonos. Profundiza en este tema y descubre cómo usar las fórmulas para hallar el área de triángulos, cuadriláteros, polígonos regulares y círculos.
¿Estás buscando cómo calcular el área de cuadriláteros, triángulos, polígonos regulares y círculos? Si es así, has llegado al lugar indicado. ¿Sabías que calcular áreas no es solo cosa de matemáticas en clase? Cuando juegas fútbol, el campo tiene forma de rectángulo (¡un cuadrilátero!), en los videojuegos los mapas y zonas seguras tienen formas geométricas, y hasta los íconos que usas en redes sociales pueden ser círculos o polígonos. Profundiza en este tema y descubre cómo usar las fórmulas para hallar el área de triángulos, cuadriláteros, polígonos regulares y círculos.
Ventajas de las fórmulas en vez de cuadrículas
Determinar el área contando cuadrículas es útil siempre y cuando la figura esté dibujada sobre un papel cuadriculado, pero, ¿qué pasa si no lo está? ¿O es figura muy grande, o está en un videojuego donde no puedes contar cuadritos?
Cuando una figura plana presenta esas condiciones es necesario la utilización de expresiones matemáticas denominadas fórmulas.
Sus ventajas son las siguientes:
- Mayor rapidez en el cálculo.
- Cálculo de cualquier tamaño.
- Aplicadas para la vida diaria.
- Permite solucionar problemas avanzados.
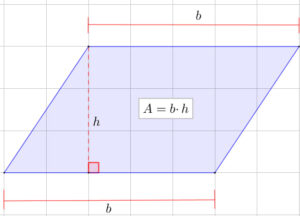
Fórmulas de áreas de los cuadriláteros
A continuación, te presentaré las fórmulas utilizadas para calcular el área de los cuadriláteros.
Rectángulo | Cuadrado |
 | 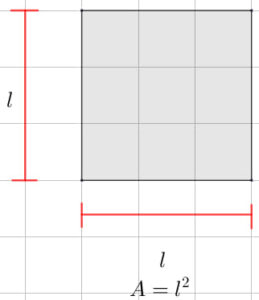 |
Trapecio | Rombo |
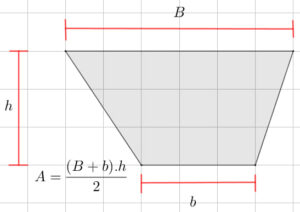 | 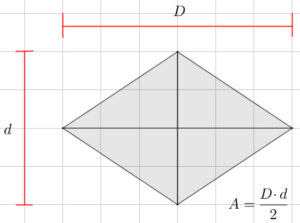 |
Romboide | |
 | |
Ejemplo
David necesita remodelar su habitación y cuenta con un plano hecho a escala 1:50. ¿Qué relación habrá entre el área del plano y su dimensión real?

Primero. Hallar el área total del plano representada en forma de rectángulo.
AP = b . h
AP = b . h = 3,6cm . 7,2cm = 25,92cm2
Segundo. Cálculo a la escala real.
Largo = 3,6cm . 50 = 180cm
Ancho = 7,2cm . 50 = 360cm
Realizando la conversión en metros queda así:
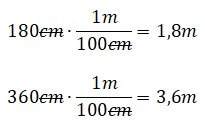
Largo 1,8m y el ancho 3,6m.
Tercero. Cálculo del área a escala real.
AR = b . h = 180cm . 360cm = 64.800m2
AR = b . h = 1,8m . 3,6m = 6,48m2
Cuarto. La relación entre el área del plano y su dimensión real.
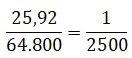
La relación entre el área del plano y su dimensión real es:

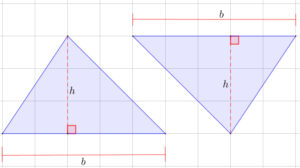
Área de un triángulo
Puedes conseguir el área del triángulo aplicando tres expresiones, pero todo depende de la situación. A continuación, las tres expresiones para hallar el área de un triángulo:
Primera (fórmula clásica). Para esta expresión debes tener el valor de la base y la altura. Pero, antes de dártela a conocer es importante que veas el siguiente proceso, de esta forma conocerás de dónde se origina ella.
- Dado un romboide.

- Trazar una diagonal. Al dibujarla, observarás la formación de dos triángulos congruentes, ahora mira la separación de ambos.

- Entonces, cada triángulo ocupa la mitad del área del romboide. Por lo tanto, la fórmula para determinar el área de uno de esos triángulos es:

Segunda (fórmula de Herón). Cuando un triángulo tiene conocidos los valores de sus tres lados, es donde se aplica la fórmula de Herón, sin necesidad de conocer la altura.
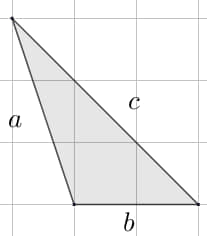
![]()
Donde:
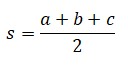
Tercera (Área del triángulo equilátero). Esta expresión es usada únicamente para calcular el área de un triángulo equilátero. Su fórmula es:

Ejemplo
Dado un el triángulo equilátero ABC de 5cm de lado. ¿Cuánto es el área sombreada de azul?
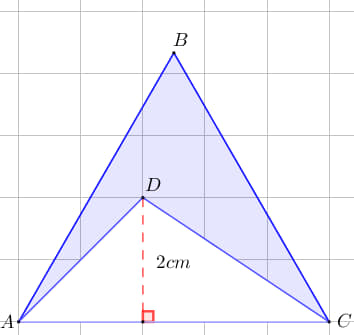
El área sombreada es un cuadrilátero y para conseguir su valor se debe restar la superficie del triángulo ABC y ADC, es decir:
![]()
Calculo del área del triángulo equilátero ABC.
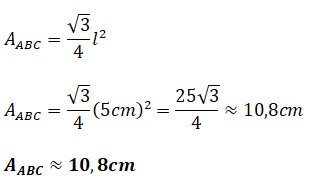
Calculo del área del triángulo equilátero ACD.
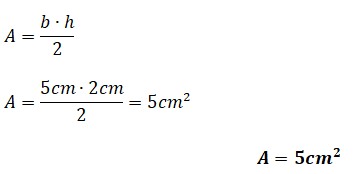
Área de un polígono regular
Cuando posees un polígono regular (A excepción del hexágono) y trazas segmentos desde los extremos de cada lado hacia el centro del polígono, obtienes finalmente triángulos isósceles.
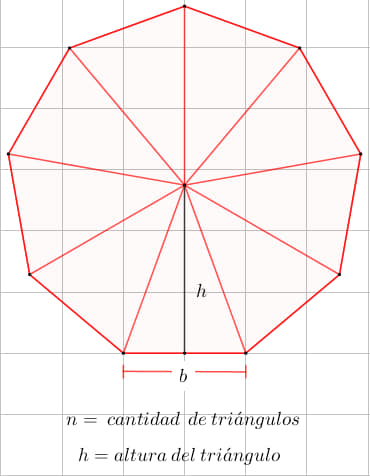
Observa el siguiente nonágono, formado por 9 triángulos isósceles, entonces, su área es:
![]()
Lo que equivale a decir que:
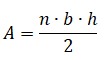
Donde:
n = cantidad de triángulos.
b = longitud de la base del triángulo.
h = altura del triángulo.
Ahora viendo el mismo nonágono sin los triángulos, queda así:
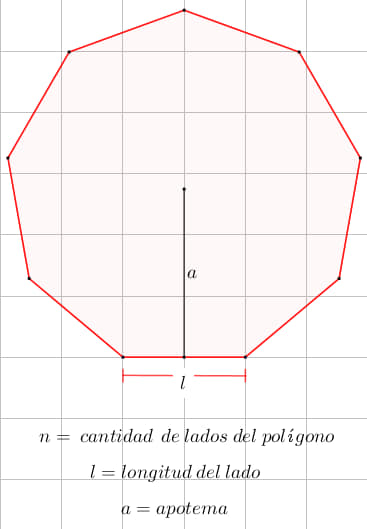
¿Qué es la apotema?
Es el segmento que tiene por extremo el centro y la mitad de cualquier lado del polígono.
Su expresión es:
![]()
Donde:
n = cantidad de lados del polígono.
l = longitud del lado.
a = apotema.
Cuando:
Se multiplica n y l se obtiene el perímetro del polígono, por lo tanto la expresión finalmente queda así:
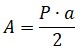
Entonces, el área de un polígono regular es la mitad del producto del perímetro y la apotema.
Ejemplo
 El rector de una escuela está pensando en adquirir mesas para los estudiantes de primer grado, el área de esta mesa tiene forma hexagonal y cada lado mide 50cm. Calcula el área de la superficie para que el director tome la decisión de cuántas mesas debe comprar.
El rector de una escuela está pensando en adquirir mesas para los estudiantes de primer grado, el área de esta mesa tiene forma hexagonal y cada lado mide 50cm. Calcula el área de la superficie para que el director tome la decisión de cuántas mesas debe comprar.
“Cuando el polígono es un hexágono regular se forman triángulos equiláteros”
Primero. Aplicar la fórmula del área de un triángulo equilátero.
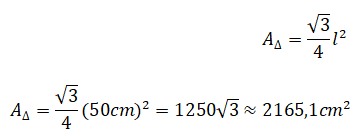
Segundo. Aplicar la fórmula clásica del cálculo del área de un triángulo, de esta forma de calcula la apotema del polígono regular:
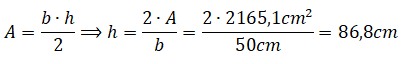
“La altura del triángulo es la apotema del hexágono”
Tercero. Calculo de la superficie de la mesa, donde:
P = n . l
P = 6 . 50cm=300cm
Al reemplazar el valor del perímetro queda:
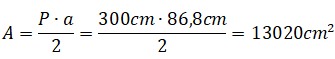
Respuesta. El área de la superficie de la mesa es de 13.020cm2.
Área del círculo
A continuación, verás un método para obtener aproximaciones más precisas al área de un círculo, el procedimiento es el siguiente:
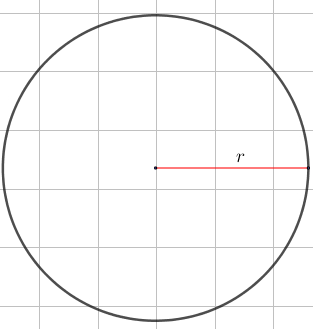
I. Construir una circunferencia y su radio.
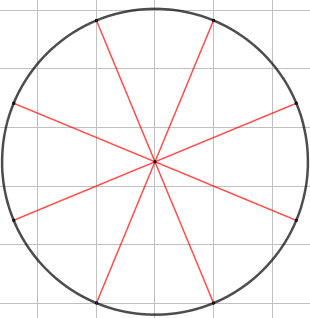
II. Dividir en partes iguales al círculo. En este caso se divide en 8 partes.
III. Distribuir cada parte de la siguiente manera llegándose a formar un romboide.
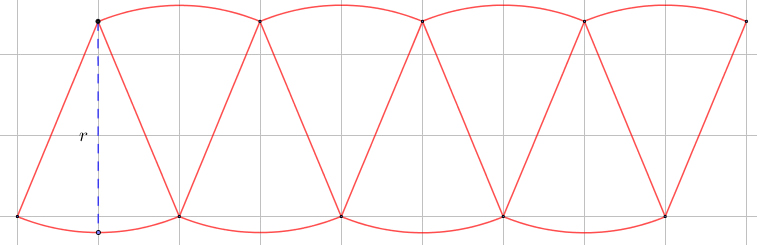
IV. Si divides el círculo en mayores partes (en este caso en 16 porciones), el área del romboide llega acercarse aún más al área del círculo. Observa la imagen:

V. La base y la altura del romboide es:

La base, como se puede observar en la imagen, corresponde a la mitad del perímetro del círculo.
Perímetro:
![]()
Base:
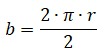
Altura:
![]()
Fórmula del romboide:
A = b . h
Al Reemplazar en la expresión:
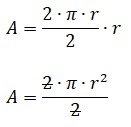
Entonces, el área del círculo es:
A = π . r2
Ejemplo
Calcular el área de un círculo que posee un diámetro de 6cm. (π = 3,1416)
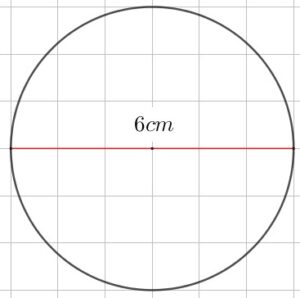
Primero. Se calcula el radio.
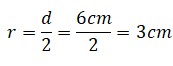
Segundo. Se calcula el área del círculo
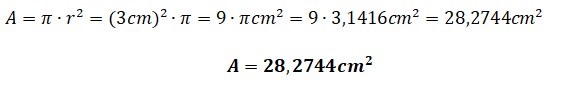
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividad
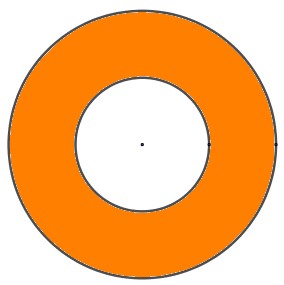
I. Determina el área sombreada, el diámetro del círculo mayor es de 10cm y del menor 5cm.
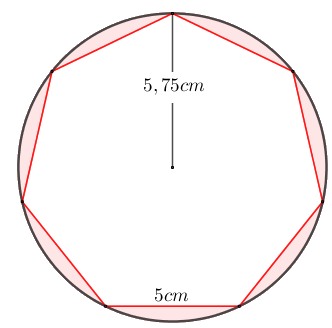
II. Calcula el área sombreada de la siguiente figura.
III. Hallar el área sombreada, las dimensiones de los radios de cada arco es expresado en la imagen a continuación:

IV. Interpreta:
- Al conocer el diámetro del círculo, ¿cómo queda la expresión para determinar el área?
- Si posees el valor del área del círculo, ¿cómo queda la fórmula para hallar el radio?
- Si tienes la longitud de la circunferencia. ¿Cómo se determina el área del círculo?
V. Hallar el área sombreada de los siguientes polígonos

VI. Diga si es verdadero o falso las siguientes afirmaciones:
- La superficie de un triángulo equilátero de lado 10cm es aproximadamente igual a 43,3cm2.
- Si el área de un triángulo equilátero es: . ¿El lado es de 6cm?
VII. Francisco comentó que: “dibujó un polígono regular donde su apotema es la mitad de su lado”. Betania dijo lo siguiente: “Eso es falso”. ¿Quién tiene la razón?