La recta la pendiente y la ecuación explícita y general

¿Sabías que la recta, la pendiente y la ecuación explícita y general no solo viven en los cuadernos de matemáticas, sino también en tu día a día? Imagina que estás planeando tus vacaciones en carretera y observas el mapa: cada ruta trazada es una recta que conecta dos puntos, pero no todas tienen la misma inclinación. Algunas suben, otras bajan, y cada una puede describirse con una pendiente diferente. Esa inclinación, que en matemáticas expresamos con una ecuación, es la que determina si tu trayecto será fácil o todo un reto.

En el mundo real, las rectas permiten analizar trayectorias, planificar caminos, diseñar rampas, calcular ángulos de visión e incluso comprender patrones en los gráficos de redes sociales o estadísticas deportivas. Entender la ecuación explícita y general te ayuda a interpretar y construir el camino más eficiente entre dos puntos, tanto en la vida como en las matemáticas.

Pendiente

La recta es una línea que pasa por al menos por dos puntos y puede presentarse en el plano cartesiano con una cierta inclinación respecto al eje x. Esta inclinación se le llama pendiente de la recta, se denota con la letra m y se calcula  dividiendo el incremento vertical entre el incremento horizontal.

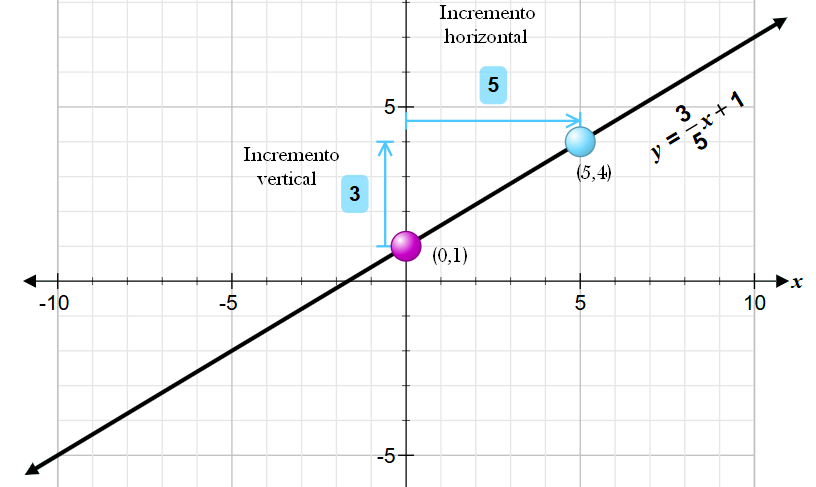
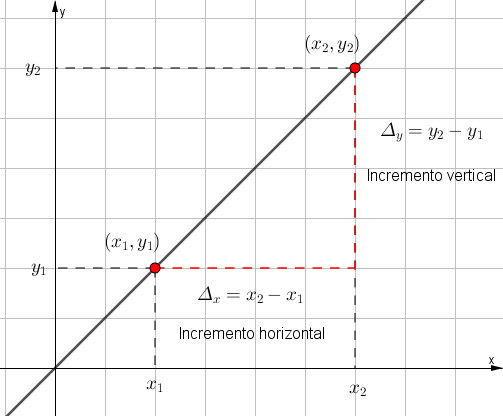
Otra forma de calcular la pendiente es aplicando la siguiente expresión:

$$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$

Donde: $$x_{2}\neq x_{1}$$

Ejemplo

Por ejemplo, calcular la pendiente de la recta que pasa por los puntos P₁(0,5) y P₂(5,-3).

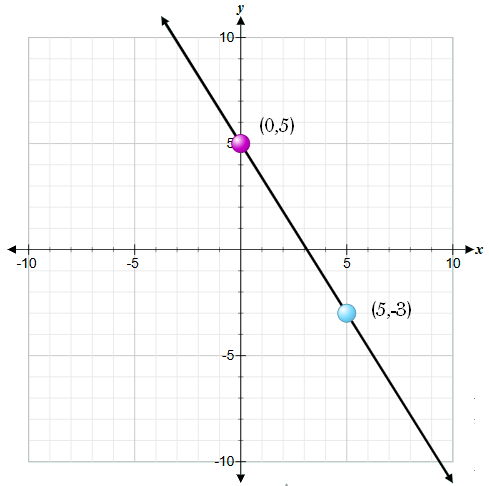
Solución

x₂ = 0; x₁ = 5; y₂ = 5; y₁ = -3

$$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$

$$m=\frac{5-(-3)}{0-5}$$

$$m=-\frac{8}{5}$$

Juega con las pendientes

🚀 Explora, mueve y descubre cómo cambia una recta cuando modificas su pendiente. En esta simulación interactiva, podrás deslizar puntos, ajustar valores y observar cómo la inclinación transforma su dirección. 🌄 ¿Sube, baja o se mantiene estable? ¡Experimenta con cada movimiento y entiende visualmente el poder de la pendiente!

✨ ¡Quiero saber tu experiencia! Después de probar la simulación de la pendiente de la recta, cuéntame en los comentarios al final del post cómo te fue. 🚀 ¿Qué notaste al mover los puntos? ¿Te sorprendió ver cómo cambia la inclinación? 🧠 Tu comentario puede ayudar a otros estudiantes a comprender mejor este concepto. ¡Anímate y comparte lo que descubriste!

Clasificación de las rectas según su pendiente

Las rectas se clasifican según su pendiente:

• Creciente.
• Decreciente
• Horizontal
• Vertical
• Idéntica.

Creciente. Es creciente cuando m>0

Puede ser una función lineal o afín

Su expresión es: $$f(x)=mx+b$$

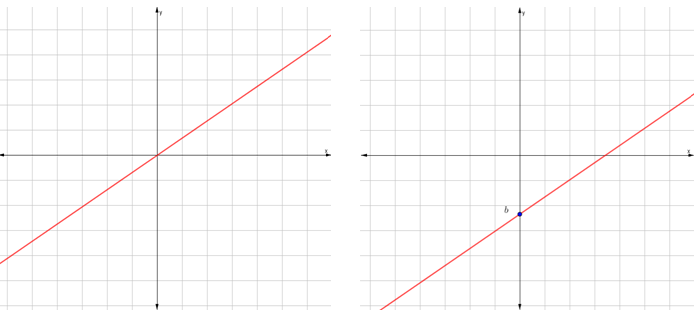
Decreciente. Cuando m<0.

Se puede comportar como una función lineal o afín

Con expresión: $$f(x)=mx+b$$

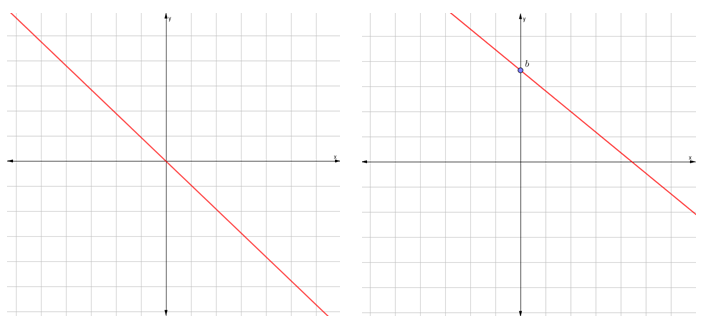
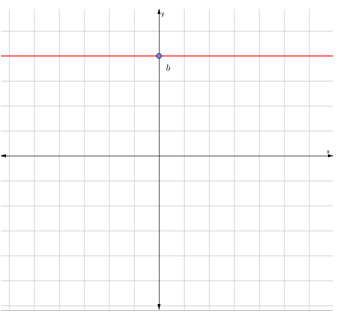
Horizontal. La m=0, b≠0

No interseca al eje x.

Expresión:$$f(x)=b$$

Es llamada función constante

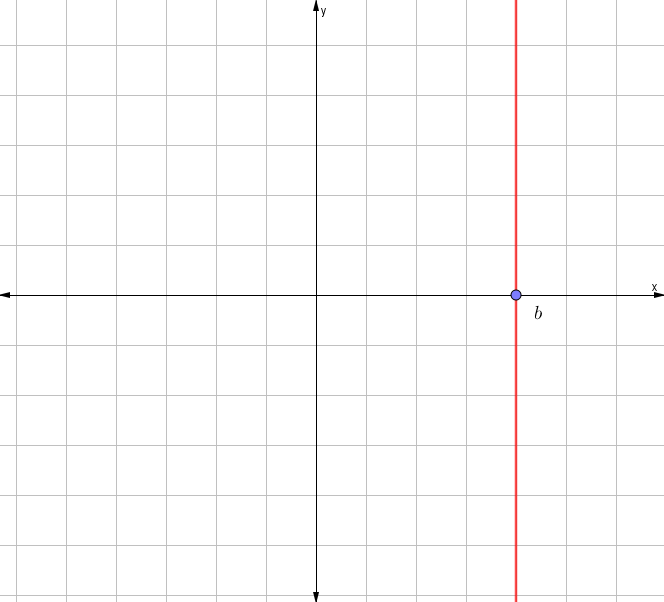
Vertical. La recta vertical posee pendiente indefinida m=∞

No interseca al eje y

Expresión:$$x=b$$

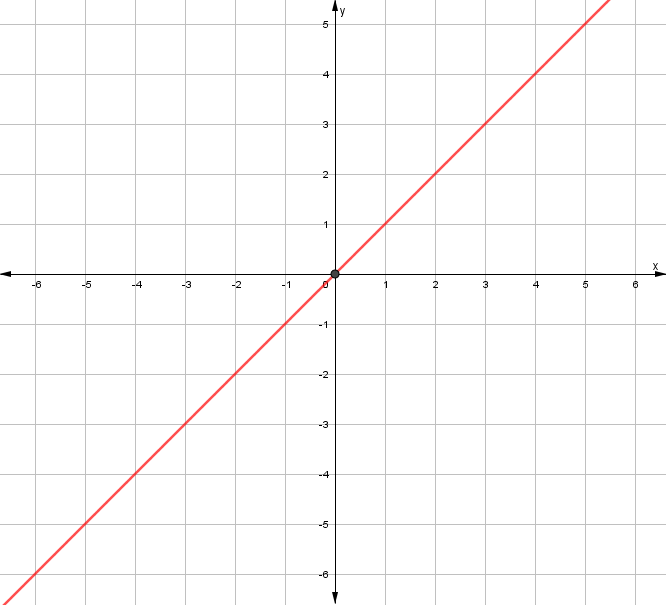
Idéntica. La m=1, b=0

La recta pasa por el origen del plano cartesiano (0,0).

Se crea un ángulo de 45° con respecto al eje x.

Expresión:$$f(x)=x$$

Ejemplo

Analiza y describa las funciones $$f(x)=4x+2$$

$$g(x)=-6x$$

Solución

Paso # 1: Identificar la pendiente de cada función.

Para$$f(x)=4x+2$$m=4 La función es creciente porque su pendiente es positiva, es decir, m>0.

y: $$g(x)=-6x$$m=-6 La función es decreciente ya que su pendiente es negativa, es decir, m<0.

Paso # 2: El valor de b.

Para la función$$f(x)=4x+2$$b=2 la recta interseca al eje y en (0,2).

$$g(x)=-6x$$ b=0, la recta pasa por el origen del plano cartesiano, por lo tanto es una función lineal.

Ecuación de la recta

Se sabe que una recta siempre pasa por al menos dos puntos, puede cortar uno o ambos ejes, y tiene una pendiente que define su inclinación. Si conoces alguno de estos elementos ya sea los puntos, la pendiente o el intercepto, puedes encontrar fácilmente la ecuación de la recta que los representa.

Tres formas diferentes para determinar la ecuación de la recta

Existen tres formas diferentes para determinar la ecuación de una recta, y cada una depende de los datos que tengas disponibles. La forma explícita, punto-pendiente.

Forma explícita

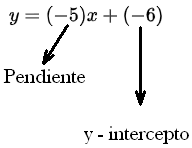
La ecuación explícita de la recta es esa que se escribe como$$y=mx+b$$ En ella, m indica qué tan inclinada está la recta y hacia dónde va, mientras que b muestra el punto donde corta el eje Y. 📉 Es una forma muy sencilla de entender cómo se comporta una recta: si es creciente, decreciente o se mantiene estable. Ideal para ver, de un vistazo, la relación entre las variables.

Ecuación de la recta dados la pendiente y el intercepto con el eje y

Para saber cuál es la ecuación de una recta teniendo la pendiente m y el intercepto b, debes reemplazar estos valores en la ecuación explícita de la recta: $$y=mx+b$$.

Por ejemplo, determina la ecuación de la recta con pendiente m=-5 e intercepto con el eje y (0,-6).

$$y=mx+b$$

$$y=-5x-6$$

Ejemplo. Determinar la ecuación de la recta cuya pendiente es m = 5 y el intercepto con el eje y es -3

Solución

Reemplazar los valores de la pendiente y el intercepto con el eje y.

$$y=mx+b$$

$$y=5x-3$$

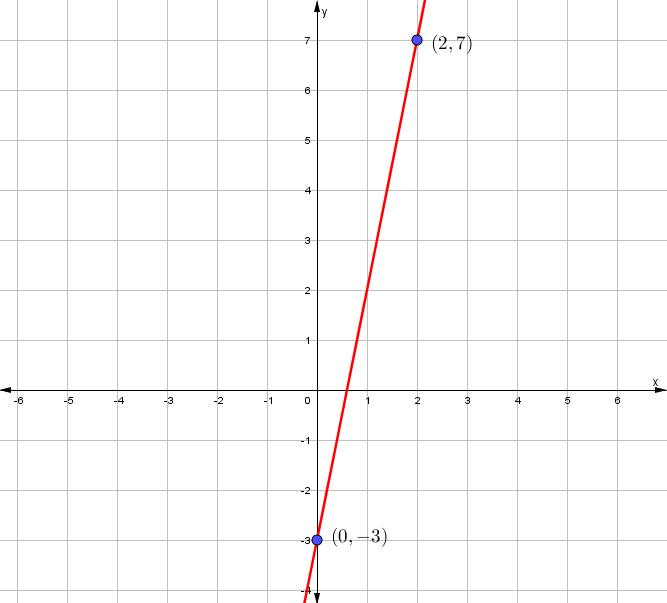
Para graficar la recta en el plano cartesiano, basta con tener dos puntos.

Primero.  Punto (0,-3) que es por donde la recta interseca al eje y.

Segundo. Evalúa la ecuación para un valor arbitrario de x. Ejemplo x = 2 y se obtiene y = 7.

Ecuación de la recta dados un punto y la pendiente

Para encontrar la ecuación de la recta dado un punto B(x,y) y su pendiente m debes cumplir con el siguiente procedimiento:

Uno. Reemplazar las coordenadas (x,y) del punto B en la ecuación explícita de la recta$$y=mx+b$$

Dos. Sustituir el valor de la pendiente m.

Tres. Despejar b.

Cuatro. Escribir la ecuación con el valor de la pendiente y del intercepto con el eje y.

Ejemplo. Determinar la ecuación de la recta que pasa por el punto (3,5) y tiene pendiente 2

Solución

Reemplazar la coordenada del punto y su pendiente.

$$y=mx+b$$

$$5=2(3)+b$$

$$5=6+b$$

Despejar b

$$b=5-6$$
$$b=-1$$

Finalmente se reemplaza el valor de la pendiente m = 2 y el intercepto con el eje y: b = -1

$$y=mx+b$$

$$y=2x+(-1)$$

$$y=2x-1$$

Resultado: $$y=2x-1$$

Ejemplo. Escriba la ecuación de la recta observa su gráfica

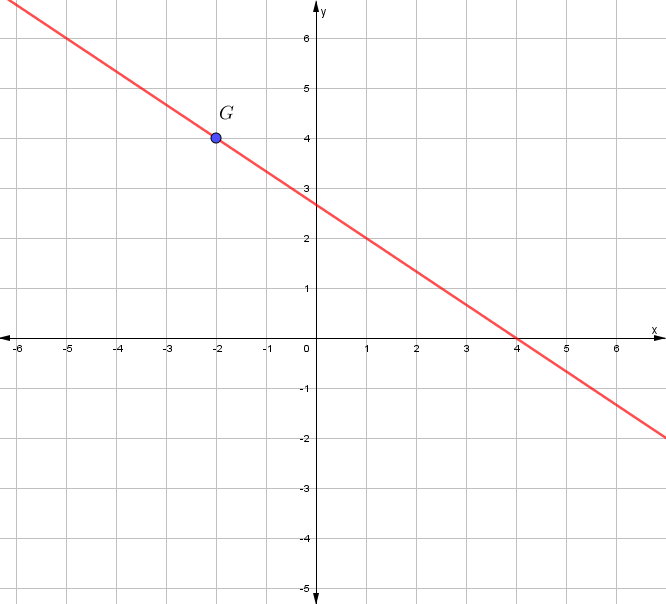
Solución

La recta pasa por el punto (-2,4) y se desplaza 3 unidades a la derecha y 2 unidades hacia abajo.

Se tiene que su pendiente es: $$m=-\frac{3}{2}$$

Como m<0 la función es decreciente.

Se reemplaza la coordenada del punto, la pendiente y se determina b.

$$4=-\frac{2}{3}(-2)+b$$

$$4=\frac{4}{3}+b$$

$$b=4-\frac{4}{3}$$

$$b=\frac{8}{3}$$

Finalmente se sustituye m y b en la ecuación explícita de la recta. $$y=-\frac{3}{2}x+\frac{8}{3}$$

Forma Punto-pendiente

La forma punto-pendiente sirve cuando conoces un punto de la recta y su pendiente. Se escribe así:$$y-y_{1}=m(x-x_{1})$$
📈 Es muy útil porque con solo esos dos datos ya puedes construir toda la recta. Te muestra cómo cambia el valor de y cuando x varía, siguiendo siempre la inclinación marcada por la pendiente.

Dados dos puntos

Si conoces dos puntos, debes calcular la pendiente de la recta, sustituir las coordenadas de un punto con su pendiente en la expresión punto-pendiente: $$y-y_{1}=m(x-x_{1})$$

Ejemplo. Hallar la ecuación de la reta que pasa por los puntos D(-1,3) y E(2,2)

Solución

Primero. Hallar la pendiente de la recta$$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$

$$m=\frac{2-3}{2-(-1)}$$

$$m=-\frac{1}{3}$$

Segundo. Sustituir el valor de la pendiente y unos de sus puntos en la ecuación de la recta.

$$y-2=-\frac{1}{3}(x-2)$$

$$y=-\frac{1}{3}x+\frac{2}{3}+2$$

Resultado:

$$y=-\frac{1}{3}x+\frac{8}{3}$$

¡A jugar! con Punto-pendiente

¿Qué pasa con una recta si cambias su pendiente o mueves el punto por donde pasa? En esta simulación de punto-pendiente podrás probarlo tú mismo: arrastra, ajusta y observa cómo la ecuación se transforma al instante. Cada movimiento te ayuda a entender mejor cómo se forma una recta y cómo la pendiente define su dirección. ¡Juega con los valores y descubre la magia detrás de una simple ecuación!

Me encantaría saber cómo te fue con la simulación de punto-pendiente. Cuéntame en los comentarios al final del post qué descubriste al mover los puntos o cambiar la pendiente. ¿Te resultó fácil entender cómo cambia la ecuación? Tu experiencia puede ayudar a otros a ver las rectas de una forma diferente. ¡Anímate a compartir lo que aprendiste!

Forma general

Es la ecuación general de la recta se escribe como:$$Ax+By+C=0$$ Es una manera más completa de representar cualquier tipo de recta, incluso las verticales y horizontales. ✏️ Lo bueno de esta forma es que no depende de despejar y, y permite ver fácilmente los coeficientes que describen la relación entre y. Es muy usada en álgebra y geometría analítica porque se adapta a casi cualquier situación.

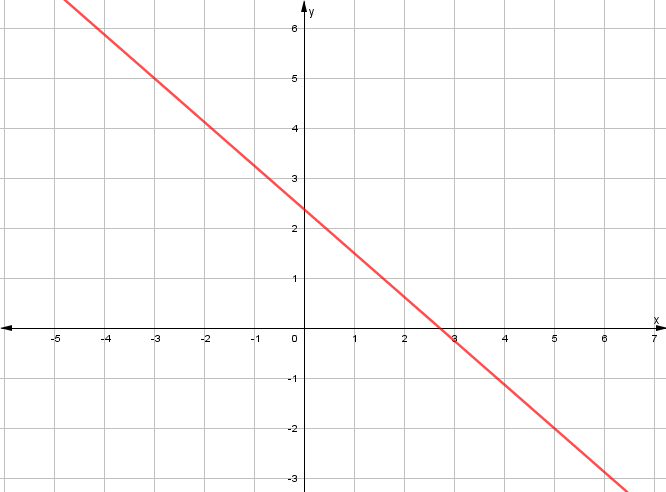
Ejemplo. Hallar la ecuación explícita de la recta que ve en la siguiente gráfica. Posteriormente calcular su ecuación general.

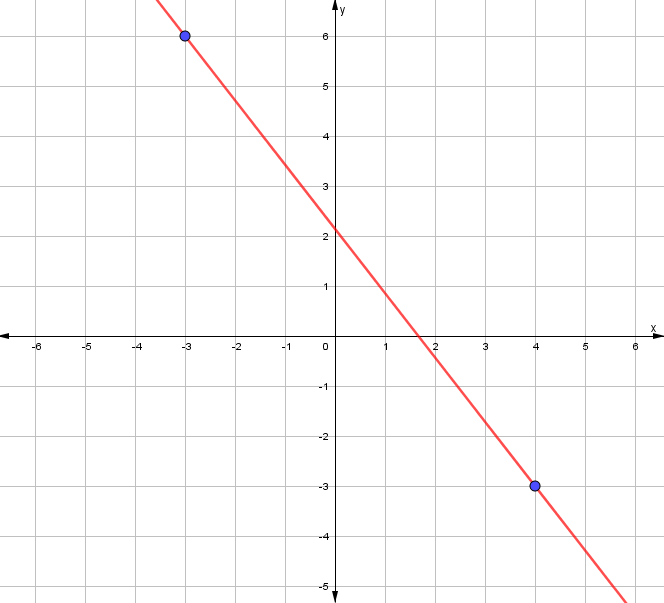
Paso 1: Seleccionar dos puntos que pertenezcan a la recta. Para este caso:

(-3,6) y (4,-3)

Paso 2: Calcular la pendiente.

$$m=\frac{-3-6}{4-(-3)}$$

$$m=-\frac{9}{7}$$

Paso 3: Utilizar la ecuación punto pendiente.

$$y-y_{1}=m(x-x_{1})$$
$$y-6=-\frac{9}{7}(x-(-3))$$
$$y-6=-\frac{9}{7}(x+3)$$
$$y-6=-\frac{9}{7}x-\frac{27}{7}$$
$$y=-\frac{9}{7}x-\frac{27}{7}+6$$
$$y=-\frac{9}{7}x+\frac{15}{7}$$

Paso 4: Multiplicar ambos miembros de la ecuación explícita por 7 e igualar a cero.

$$7y=-9x+15$$
$$7y+9y-15=0$$

Resultado: La ecuación general es:

$$7y+9y-15=0$$

Reto de la recta la pendiente y la ecuación explícita y general: demuestra lo que sabes en 6 niveles de desafío

¿Listo para poner a prueba todo lo que sabes sobre la recta, su pendiente y sus ecuaciones? En este reto interactivo de 6 niveles, deberás aplicar tus conocimientos paso a paso, desde lo más sencillo hasta los casos más complejos. 🚀 Cada nivel te reta a pensar, calcular y visualizar cómo cambian las rectas según los datos que se te dan. ¡Demuestra tu habilidad y llega hasta el final del desafío!

Ahora quiero saber cómo te fue con el Reto de la recta. Cuéntame en los comentarios al final del post hasta qué nivel llegaste y qué parte te pareció más difícil o divertida. 🎮 Tu experiencia puede motivar a otros a intentarlo también. ¡Anímate a dejar tu opinión!

Actividades de la recta la pendiente y la ecuación explícita y general

I.Identifica la pendiente y el intercepto con el eje y en cada una de las ecuaciones.

$$4x+1=y$$
$$y=-5x+3$$
$$y=3x-1$$
$$y=-1-8x$$
$$y=1+2x$$
$$y=-8-7x$$

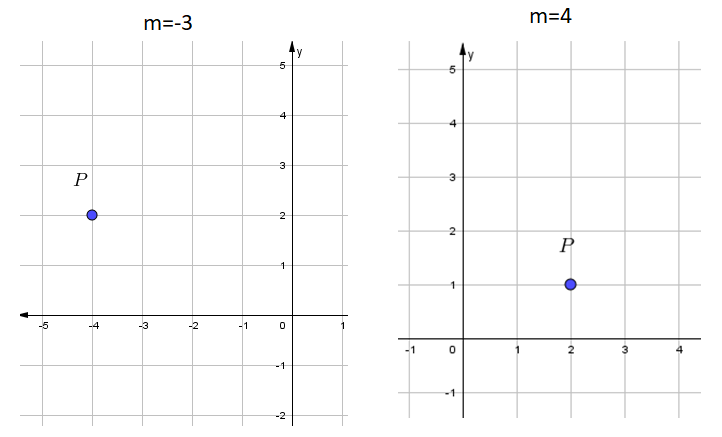
II.Determinar la ecuación de la recta que pasa por el punto que se indica en el plano cartesiano y que tiene la pendiente indicada en cada caso.

III.Diga si es verdadero o falso las siguientes afirmaciones. Justifica tu respuesta.

🎯Todas las rectas cuyas pendientes son positivas, intersecan al eje y en un punto (0,b) donde b ≥0.

↔️Si la ecuación explícita de una recta es y=b, interseca al eje y en b con pendiente = 0.

✋Todas las rectas x = c no poseen pendiente.

IV.Hallar la ecuación explícita de cada recta que pasa por un punto y tiene pendiente m. Utiliza la ecuación punto pendiente.

A(-2,8); m = 2.

B(-1,7); m = -2.

C(-5,-3); m = 2/3.

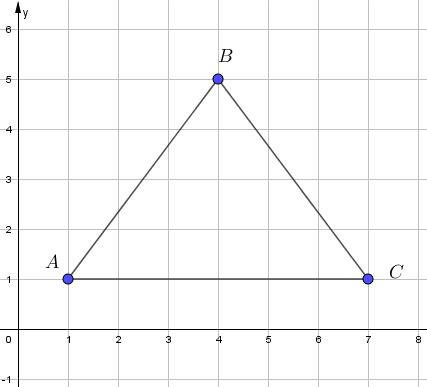
V.Calcular las ecuaciones de la recta, el intercepto con el eje y y el punto de corte con el eje x de todas las rectas que forman el triángulo.

VI.Escribe la forma general de las siguientes expresiones de la recta.

$$y=2x+3$$
$$y=7x-5$$
$$y=-3x+10$$
$$y=-\frac{2}{9}x-\frac{9}{5}$$

VI.Escribe la ecuación general de la recta que se muestra en la imagen.

Javier Guzmán

laprofematematik.co/