¿Sabías que usas fracciones todos los días sin darte cuenta? Las fracciones no solo están en las clases de matemáticas, también aparecen cuando juegas, compartes en redes sociales o ves tus series favoritas. Por ejemplo: al completar 3 de 4 misiones en un videojuego, ¡has avanzado las tres cuartas partes del reto! Y si 250 de tus 1.000 seguidores ven tu historia, eso significa que ¼ del total la ha visto. Las fracciones pueden parecer abstractas, pero tienen aplicaciones todo el tiempo en la vida diaria.
¿Qué es una fracción?
Es la representación de las partes que se escogen de un todo y se escribe así: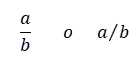 Donde: a = es el numerador. b = el denominador. |
¿Qué función cumple el numerador y el denominador en las fracciones?
El numerador indica las partes que se toman, mientras que, el denominador muestra el total de partes iguales que divide a un todo.
Ejemplo: En el día de hoy está de cumpleaños, Albert, Luis y Vinicio. La profesora de matemáticas fracciona el pastel en 3 partes iguales y toma una de ellas para dársela a Vinicio. Representa la fracción que recibió Vinicio.
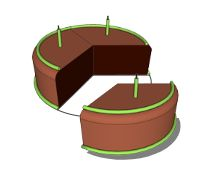
Vinicio recibió 1/3 del pastel, donde el numerador 1 representa una parte tomada y el denominador 3 expresa el total de partes iguales.
Lectura de fracciones
Leer correctamente las fracciones ofrece muchas ventajas: permite razonar con mayor precisión, expresar ideas con claridad, participar con seguridad y comprender mejor distintas situaciones.
Existen tres formas de leer una fracción, y todo depende del valor del denominador.
Para leerla correctamente, sigue estos pasos:
- Identifica qué forma de fracción es.
- Menciona el número del numerador.
- Luego, di el nombre correspondiente al denominador.
A continuación, las tres formas de leer una fracción según el valor del denominador:
- Uno (denominadores simples).
- Dos (denominadores de potencias 10).
- Tres (denominadores extensos).
Uno (denominadores simples)
Si el denominador posee valores comprendidos desde el 2 hasta el 9, su lectura es la siguiente:
| Denominadores simples | ||
| Denominador | Lectura | Ejemplo |
| 2 | medio | 5/2 cinco medios |
| 3 | tercio | 7/3 siete tercios |
| 4 | cuarto | 1/4 un cuarto |
| 5 | quinto | 6/5 seis quintos |
| 6 | sexto | 1/6 un sexto |
| 7 | séptimo | 3/7 tres séptimos |
| 8 | octavo | 1/8 un octavo |
| 9 | noveno | 5/9 cinco noveno |
Dos (denominadores de potencias 10)
Cuando posea cantidades formadas por la unidad seguida de ceros (10,100, 1 000,…), se le agrega el sufijo: ésimas o ésimos dependiendo del contexto.
| Denominadores de potencias 10 | ||
| Denominador | Lectura | Ejemplo |
| 10 | décimas | 3/10 tres décimas |
| 100 | centésimas | 1/100 una centésima |
| 1 000 | milésimas | 7/1 000 siete milésimas |
| 10 000 | diezmilésimas | 11/10 000 once diezmilésimas |
| 100 000 | cienmilésimas | 1/100 000 cienmilésimas |
| 1 000 000 | una millonésima | 5/1 000 000 cinco millonésimas |
| 10 000 000 | diezmillonésimas | 3/10 000 000 tres diezmillonésimas |
| 100 000 000 | cienmillonésimas | 13/100 000 000 trece cienmillonésimas |
Tres (denominadores extensos)
Pertenecen a todos los demás números, estas cantidades se les agrega el sufijo: avos.
Observación: En la tabla aparece D = denominador.
| Denominadores extensos | ||
| D | Lectura | Ejemplo |
| 11 | onceavos | 2/11 dos onceavos |
| 13 | treceavos | 1/13 un treceavos |
| 24 | veinticuatroavos | 1/24 un veinticuatroavos |
| 105 | cientocincoavos | 2/105 dos cientocincoavos |
| 600 | seiscientosavos | 7/600 siete seiscientosavos |
| 1700 | milsetecientosavos | 3/1 700 tres milsetecientosavos |
| 45000 | cuarentaycincomilavos | 1/45 000 un cuarentaycincomilavos |
| 15 | quinceavos | 13/15 trece quinceavos |
Clasificación de las fracciones
Las fracciones se clasifican dependiendo de los valores del numerador y del denominador. Ellos son los siguientes:
- Fracción unidad.
- Fracciones propias.
- Fracciones impropias.
- Fracciones nulas.
- Fracciones enteras.
- Fracciones decimales.
- Fracciones complementarias.
Fracción unidad
Se le da este nombre cuando el numerador posee el mismo valor que el denominador resultando un valor igual a 1, es decir:
a = b
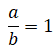
Ejemplo: La profesora partió el pastel en tres partes iguales y le pidió a uno de los estudiantes que la fotografiaran. Escriba la fracción de esta situación.
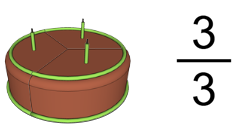
Respuesta: Observa, el pastel está fraccionado en tres partes iguales, entonces la respuesta es una fracción unidad, ya que no se ha tomado ninguna de ellas, por lo tanto:
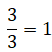
Fracciones propias
Sucede cuando el numerador < denominador, es decir: a < b.
Ejemplo: ¿Qué fracción de agua posee el envase que se muestra en la imagen?
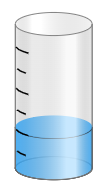
Respuesta: Posee 2/7
Fracciones impropias
Son impropias si se cumple que a > b, es decir, el numerador mayor que el denominador.
Por ejemplo: Luis y sus amigos pidieron 3 pizzas iguales para ver el juego de fútbol. Cada pizza estaba cortada en 3 partes iguales. ¿Cuántas partes se comieron?
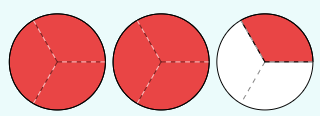
Luis y sus amigos se comieron todas las porciones de las dos primeras pizzas.
Es decir, consumieron 2 pizzas. Al sumar ambas fracción unidad el resultado es:
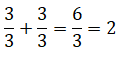
La tercera pizza sólo se comió 1 de las tres porciones.
¿Cuántas partes se comieron?
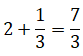
Como es una fracción impropia se puede transformar en un número mixto, quedando de la siguiente forma:
$$\frac{7}{3}=2\frac{1}{3}$$
Respuesta: Se comieron: $$\frac{7}{3}=2\, \frac{1}{3}\, \, \, pizzas$$
Fracciones nulas
Son aquellas que el numerador posee un valor igual a cero. Es decir, a = 0.
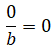
Ejemplo: Exprese la cantidad de líquido existente en el envase, sabiendo que el mismo está dividido en siete partes iguales.
Respuesta: No posee líquido por lo tanto su contenido es: 0/7
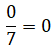
Fracciones enteras
Es una fracción impropia en la que el numerador es un múltiplo exacto del denominador, lo que significa que al dividir se obtiene un número entero.
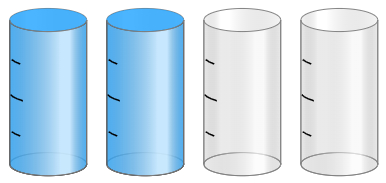
Ejemplo: Observe los envases graduados (cada uno dividido en 4 partes iguales) e interprete la cantidad total de líquido expresada como una fracción.
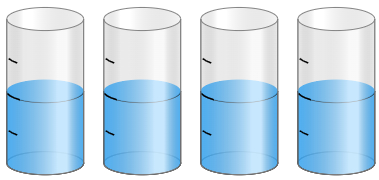
Respuesta:
Cada cilindro posee: 2/4
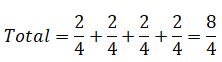
Observa la imagen. ¿Qué interpretas? El líquido de los dos últimos envases fue vertido en los dos primeros, logrando así 2 envases completamente llenos.
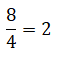Todo número entero es múltiplo de 1, entonces, toda fracción cuyo denominador es 1 es también una fracción entera. Por ejemplo:
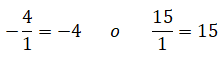
Fracciones decimales
Las fracciones decimales poseen como denominador a la unidad seguida de ceros. Ejemplo:
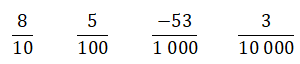
| 😯 Curiosidad: Existen fracciones propias e impropias que al amplificarlas (complificarlas) pueden transformarse en fracciones decimales siempre y cuando el denominador posea factores 2 y/o 5. |
Ejemplo # 1: Transforma las siguientes fracciones a fracciones decimales: 8/50 ; -5/4 ; 1/2 ; 21/4.
Análisis: Al descomponer los denominadores de todas las fracciones poseen factores 2 y/o 5. Por esta razón pueden convertirse a fracción decimal.
Ejemplo # 2: Convierte las siguientes fracciones a fracciones decimales: 7/3 ; 54/11 ; 27/17.
Análisis: No se pueden convertir en fracciones decimales ya que la descomposición de sus denominadores no contienen factores 2 y/o 5.
Fracciones complementarias
Es la suma de fracciones propias generando una fracción unidad. Por ejemplo:
Ejemplo: Camila tiene una barra de chicle sabor a fresa dividida en 5 partes iguales. Ella se come 2/5 de la barra por la mañana y 1/5 por la tarde. ¿Se comió toda la barra de chocolate? Justifica tu respuesta.
Solución:
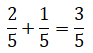
En el día se comió 3/5
Entonces, para saber si se comió toda la barra se resta la fracción unidad (barra de chicle) y la fracción consumida.
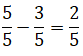
Respuesta: Camila no se comió toda la barra de chicle dejó dos porciones de 5.
2/5
Interpretación: Al sumar ambas fracciones (consumida y la que dejó) genera la fracción unidad.
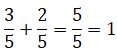
Entonces, ambas fracciones son complementarias, porque al sumarlas se obtiene el total (la unidad).
¡A jugar! ingresa al laboratorio de las fracciones
Llegó el momento de probar tus conocimientos, explora la simulación jugando, luego construye fracciones usando números e imágenes, cambia los numeradores y los denominadores de la fracción de tu preferencia y explica como afecta el valor de la fracción.
Prueba la simulación y cuéntame en los comentarios que te pareció.
Actividades
1.Clasifica las siguientes fracciones como unidad, impropia o propia y transfórmalas a fracción decimal (las fracciones que permitan).
| a) | 3/5 | g) | 25/25 |
| b) | 7/3 | h) | 17/17 |
| c) | 92/12 | i) | 120/120 |
| d) | 310/98 | j) | 160/200 |
| e) | 5/6 | k) | 60/74 |
| f) | 123/325 | l) | 1000/1000 |
2.Completa cada fracción para que su clasificación sea la correspondiente.
| a) | Unidad ___/23 | g) | Entera 12/___ |
| b) | Nula ___/55 | h) | Decimal 46/___ |
| c) | Decimal 39/___ | i) | Unidad 105/___ |
| d) | Impropia 13/___ | j) | Entera ___/14 |
| e) | Propia 15/___ | k) | Impropia 34/___ |
| f) | Decimal 37/___ | l) | Propia ___/200 |
3.Halla la fracción complementaria.
| a) | 2/5 | c) | 5/83 | e) | 23/86 |
| b) | 3/7 | d) | 2/105 | f) | 2/200 |
4.Transforma las siguientes fracciones impropias en números mixtos.
| a) | 13/2 | c) | 33/9 | e) | 61/3 |
| b) | 23/11 | d) | 23/5 | f) | 105/14 |
Comparte esto:
Descubre más desde LaProfematematiK "Dios es Bueno"
Suscríbete y recibe las últimas entradas en tu correo electrónico.