¿Sabes cómo determinar el dominio de una función?
Antes de aprender a calcularlo, es fundamental comprender qué significa. El dominio de una función es el conjunto de valores de la variable independiente 𝑥 para los cuales la función está definida. Dicho de otra manera, corresponde al primer valor de cada par ordenado, y gráficamente se ubica sobre el eje de las abscisas o eje 𝑥.
Para relacionar este concepto con la vida diaria, conozcamos a don Raúl, un abuelito que vive con su nieto y ambos trabajan vendiendo jugo de caña. Él me cuenta su rutina:
- Va al campo donde tiene sembrada la caña.
- Corta la caña.
- Troza la caña de azúcar en pedazos pequeños.
- Pela cada pedazo.
- Introduce los trozos en la máquina exprimidora.
- Finalmente, obtiene el delicioso jugo de caña.
Ahora bien, observa la imagen del paso 4: cada trozo de caña de azúcar representa un elemento del dominio. Es decir, el dominio es como el conjunto de todos esos trozos, los cuales permiten obtener el resultado final de la función.

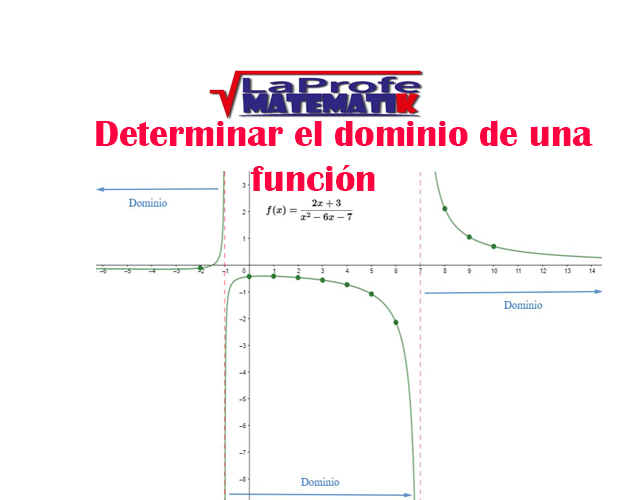
Dominio de una función gráficamente
A continuación, observa la siguiente imagen donde se puede mostrar el dominio de una función:
 |
Para poder representar gráficamente esa curva, se sustituyen los valores arbitrarios de “x” en la función dada, estos valores son pertenecientes al dominio o conjunto de partida.
En la imagen anterior la curva de color verde viene del – ∞ y se va hacia el + ∞ del eje “x”, esto quiere decir que el dominio de esta función son todos los valores del eje “x”, es decir, todos los números reales ℜ.
Definición
| El dominio de una función es el conjunto de todos los números reales ℜ y se representa como: Dom f = ℜ = (-∞,∞). También se puede definir como el conjunto de valores que puede tomar la variable dependiente “y”. |
El dominio en un diagrama sagital pertenece al conjunto de partida y en una representación gráfica está ubicado en el eje “x” del plano cartesiano.
Ejemplo:
Determina el dominio del siguiente conjunto de pares ordenados: f = {(1,5),(2,7),(3,9),(4,11),(5,13)
Nota: Ten en cuenta que el dominio es el conjunto de partida, también es el primer número de cada par ordenado.
Respuesta: El dominio de la función es:
Dom(f) = { 1,2,3,4,5}
Función definidas
Una función está definida cuando el conjunto de los números reales ℜ son utilizados en el conjunto de partida o en el Dominio y el único conjunto de números que pueden estar en el conjunto de llegada o Rango son los números reales ℜ.
Restricciones del dominio
La restricción del dominio ocurre cuando ciertos valores de la variable independiente 𝑥 provocan que la función no tenga un resultado válido para la variable dependiente 𝑦. En otras palabras, son los casos en los que la función se vuelve indefinida o no pertenece a los números reales. En este post se mencionará tres tipos.
Ejemplo de cada restricciones
Restricción # 1
Cuando existen raíces de índices pares de un número negativo.
Ejemplo: Dada la función \(f(x)=\sqrt{x}\) este tipo de expresión la raíz es de índice par y no está definida para valores negativos, observe:
| Valor | Expresión | Observación |
| $$x=-1$$ | $$f(-1)=\sqrt{-1}$$ | No tiene solución en los números reales ℜ Esto quiere decir que la variable dependiente no toma valor |
Restricción # 2
Fracciones donde se anula el denominador.
Ejemplo # 3: Dada la función \(f(x)=\frac{1}{x-3}\) este tipo de expresión no está definida para cuando x = 3.
| Valor | Expresión | Observación |
| $$x= 3$$ | $$f(x)=\frac{1}{3-3}$$ | No tiene solución en los números reales ℜ El denominador no puede ser cero. |
Restricción # 3
Fracciones donde se anulan el denominador y con raíces de índices par en el numerador.
Ejemplo: Dada la función \(f(x)=\frac{\sqrt{x-1}}{x^{2}-9}\) no está definida para valores negativos por estar una raíz de índice par, tampoco está definida cuando x = 3 en el denominador
| Valor | Expresión | Observación |
| $$x = -3$$ | $$f(x)=\frac{\sqrt{-3-1}}{-3^{2}-9}$$ | No tiene solución en los números reales ℜ. |
Determinar el dominio con restricción
Restricción # 1: Raíces con índices pares
Para que la función esté definida es necesario que la cantidad subradical sea mayor o igual a cero, es decir, resolverla a través de una inecuación.
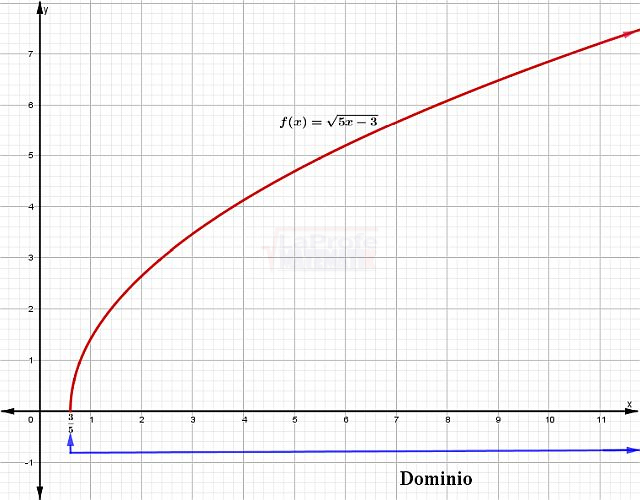
Ejemplo: Determinar el dominio de la función:
$$f(x)=\sqrt{5x-3}$$
| 1 | Expresar la cantidad subradical como mayor o igual cero | $$5x-3\geq 0$$ |
| 2 | Despejar el valor de «x» | $$x\geq \frac{3}{5}$$ |
| 3 | El resultado nos quiere decir que: | Está definida para todos los valores reales de 𝑥 mayores o iguales que 3/5 |
| 5 | Entonces el intervalo de valores que toma la variable o el dominio de la función es: | $$D_{f}=[3/5,\infty )$$ |
Observa la gráfica
Restricción # 2: Fracciones donde se anula el denominador
Para que la función esté definida es necesario que el denominador sea distinta a cero.
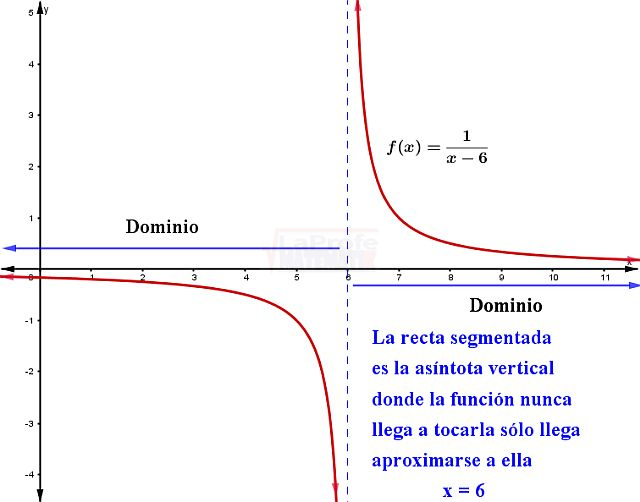
Ejemplo # 1: Determine el dominio de la función:
$$f(x)=\frac{1}{x-6}$$
| 1 | Expresar la cantidad del denominador distinto a cero | $$x-6\neq 0$$ |
| 2 | Despejar «x» | $$x\neq 6$$ |
| 3 | Entonces el dominio de la función es: | $$D_{f}=\mathbb{R}-\left\{ 6\right\}$$ |
| 4 | Observaciones | Existe una asíntota vertical, esto quiere decir que el dominio de la función es todo el conjunto de los números reales menos el 6 ya que la curva nunca llega a tocar la asíntota sólo se aproxima a ella. |
Observa la gráfica:
Ejemplo # 2: Determine el dominio de la función
$$f(x)=\frac{2x+3}{x^{2}-6x-7}$$
Paso # 1: Expresar el denominador distinto a cero.
$$x^{2}-6x-7\neq 0$$
Paso # 2: Factorizar la expresión o aplicar la resolvente.
$$(x+1)(x-7)\neq 0$$
Paso # 3: Obtener el valor de “x”
$$x+1\neq 0$$
$$x\neq -1$$
$$x-7\neq 0$$
$$x\neq 7$$
Paso # 4: Construcción de la tabla de valores
| x | -2 | -1 | 0 | 1 | 2 | 7 |
| f(x) | $$-\frac{1}{9}$$ | $$\infty $$ | $$-\frac{3}{7}$$ | $$-\frac{5}{12}$$ | $$-\frac{7}{15}$$ | $$\infty $$ |
Observa que en x = –1 y en x = 7 la función se hace indefinida, por lo tanto la curva no pasa por ellos.
Paso # 5: Gráfica
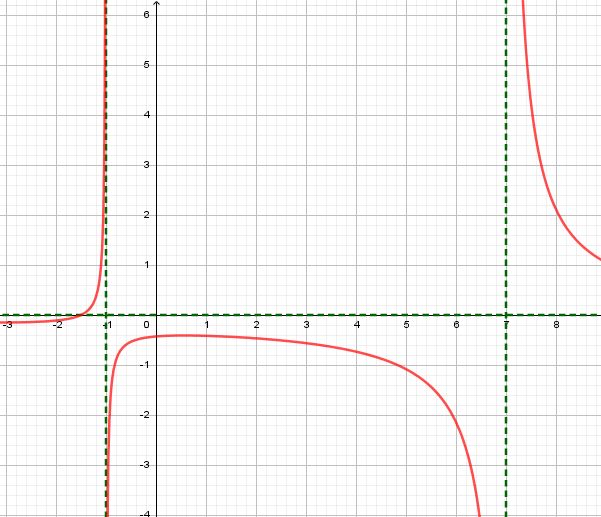
Paso # 6: Cálculo del dominio.
Entonces la variable puede tomar cualquier valor real menos del -1 y del 7. Entonces el dominio es:
$$D_{f}=(-\infty ,-1)\cup (-1,7)\cup (7,\infty )$$
Restricción # 3: Fracciones donde se anula el denominador con raíces de índices par
Este caso la variable se encuentra como cantidad subradical en una raíz de índice par y también en el denominador.
Ejemplo # 8: Determine el dominio de la función
$$f(x)=\frac{\sqrt{4x+3}}{7-x}$$
1 Resolver el numerador
$$4x+3\geq 0$$
$$x\geq -\frac{3}{4}$$
2 Resolver el denominador:
$$x\neq 7$$
4 Entonces el dominio de la función es:
$$D_{f}=\left [ -\frac{3}{4},\infty \right )\cup (7,\infty )$$
5 Construcción de la tabla de valores.
Para graficar lo primero es crear la tabla de valores, tomando en cuenta el valor mínimo del dominio de la función.
En este caso
valor mínimo : -3/4
| x | -3/4 | 0 | 1 | 2 | 7 | 8 |
| f(x) | 0 | $$\frac{\sqrt{3}}{7}$$ | $$\frac{\sqrt{7}}{6}$$ | $$\frac{\sqrt{11}}{5}$$ | $$\infty $$ | $$\sqrt{35}$$ |
- Construcción de la gráfica.
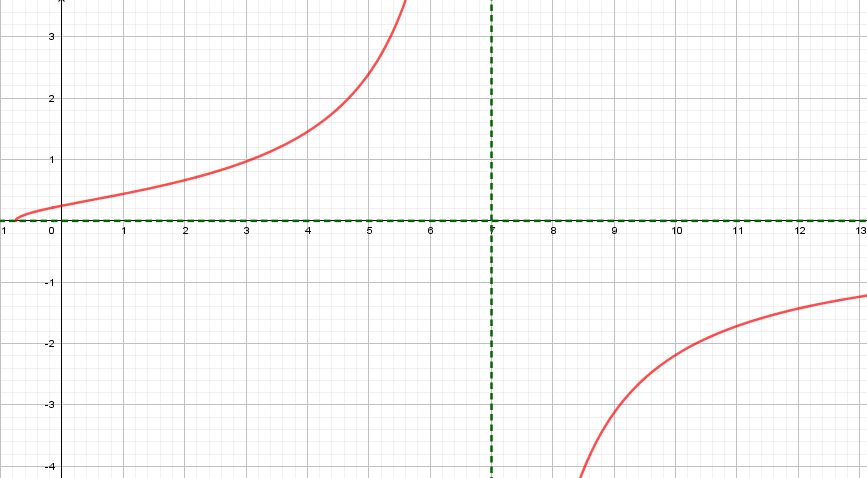 |
Actividades
Determinar el dominio de cada una de las siguientes funciones mencionando si existe o no restricciones
$$1.) f(x)=\sqrt{x-5}$$
$$2.) f(x)=\sqrt{2x+7}$$
$$3.) f(x)=\sqrt{9-x^2}$$
$$4.) f(x)=\frac{1}{x-4}$$
$$5.) f(x)=\frac{x+2}{x^2-9}$$
$$6.) f(x)=\frac{3x}{x^2+2x-15}$$
$$7.) f(x)=\frac{\sqrt{x+1}}{x-2}$$
$$8.) f(x)=\frac{\sqrt{2x-3}}{x^2-16}$$
$$9.) f(x)=\frac{\sqrt{5-x}}{x^2-1}$$
$$10.) f(x)=\frac{\sqrt{x^2+4x}}{x+7}$$
Soluciones:
$$1.) D=[5,\infty)$$
$$2.) D=\left[-\tfrac{7}{2},\infty\right)$$
$$3.) D=[-3,3]$$
$$4.) D=\mathbb{R}\setminus{4}$$
$$5.) D=\mathbb{R}\setminus{-3,3}$$
$$6.) D=\mathbb{R}\setminus{-5,3}$$
$$7.) D=[-1,\infty)\setminus{2}$$
$$8.) D=\left[\tfrac{3}{2},\infty\right)\setminus{-4,4}$$
$$9.) D=(-\infty,5]\setminus{-1,1}$$
$$10.) D=(-\infty,-4]\cup[0,\infty)\setminus{-7}$$