 ¿Te has preguntado qué utilidad tienen las inecuaciones y desigualdades en nuestra vida diaria? Están presentes en situaciones cotidianas, como la clasificación de edad de una película: si la restricción es «Para mayores de 16 años,» esta se traduce en la desigualdad Edad ≥ 16. Pero, ¿sabes cómo resolver problemas más complejos que involucran la misma lógica de restricción? En este post, te mostraré de ese simple ejemplo hasta el dominio total de las inecuaciones lineales, racionales y con valor absoluto, enseñándote el método paso a paso para que puedas solucionar cualquier desigualdad matemática que se te presente.
¿Te has preguntado qué utilidad tienen las inecuaciones y desigualdades en nuestra vida diaria? Están presentes en situaciones cotidianas, como la clasificación de edad de una película: si la restricción es «Para mayores de 16 años,» esta se traduce en la desigualdad Edad ≥ 16. Pero, ¿sabes cómo resolver problemas más complejos que involucran la misma lógica de restricción? En este post, te mostraré de ese simple ejemplo hasta el dominio total de las inecuaciones lineales, racionales y con valor absoluto, enseñándote el método paso a paso para que puedas solucionar cualquier desigualdad matemática que se te presente.
Inecuaciones
| Las inecuaciones son expresiones algebraicas que incluye una desigualdad, determinando un conjunto de valores. |
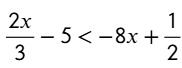
Desigualdades
 Las desigualdades son relaciones que permite comparar dos cantidades y determinar si una es mayor, menor, mayor o igual, o menor o igual que la otra.
Las desigualdades son relaciones que permite comparar dos cantidades y determinar si una es mayor, menor, mayor o igual, o menor o igual que la otra.
A diferencia de una igualdad, donde las dos expresiones son equivalentes, en una desigualdad las expresiones no son necesariamente iguales, sino que establece una relación de orden entre ellas.
Sus símbolos son:
$$>\; \left ( mayor\;que \right )$$
$$\leq \left ( menor\;que \right )$$
$$\geq \left ( mayor\;o\;igual\;que \right )$$
$$\leq \left ( menor\;o\;igual\;que \right )$$
Ejemplo:
$$15+3>16$$
Las desigualdades se clasifican en:
- Desigualdades estrictas.
- Desigualdades no estrictas.
Principales propiedades de las desigualdades
Las propiedades de las desigualdades ayudan a trabajar con las inecuaciones e aquí algunas de ellas:
- Propiedad #1: Si ambas partes de una desigualdad se multiplican (o dividen) por una misma cantidad negativa, la desigualdad cambia de sentido. Ejemplo:
| En la multiplicación | En la división |
| $$10>6$$ | $$-12<18$$ |
| $$10(-1)<6(-1)$$ | $$\frac{-12}{-2}> \frac{18}{-2}$$ |
| $$-10<-6$$ | $$6>-9$$ |
- Propiedad #2: Si ambas partes de una desigualdad se multiplican (o dividen) por una misma cantidad positiva, la desigualdad No cambia de sentido. Ejemplo:$$10>8$$
| En la multiplicación | En la división |
| $$5>4$$ | $$5>4$$ |
| $$5(2)>4(2)$$ | $$\frac{5}{2}< \frac{4}{2}$$ |
| $$10>8$$ | $$\frac{5}{2}> 2$$ |
- Propiedad #3: Si ambas miembros de la desigualdad son positivos y se eleva a un exponente impar positivo No cambia el sentido de la desigualdad. Ejemplo:
$$-3<1$$
$$(-3)^{3}<(1)^{3}$$
$$-27<1$$
- Propiedad #4: Si ambos miembros de la desigualdad son de distintos signos y al elevarse a un exponente par positivo, cambia el sentido de la desigualdad o también puede convertirse en una igualdad. Ejemplo:
$$-4<3$$
$$(-4)^{2}>(3)^{2}$$
$$16>9$$
Otro ejemplo:
$$4>-4$$
$$(4)^{2}=(-4)^{2}$$
$$16=16$$
- Propiedad #5: Si ambos lados de la desigualdad son del mismo signo, los inversos producen una desigualdad de sentido opuesto. Ejemplo:
$$9< 10$$
$$\frac{1}{9}> \frac{1}{10}$$
Soluciones de una inecuación
 Los valores que satisfacen una ecuación es llamado soluciones, raíces o ceros. En una inecuación los valores de la variable que satisface a dicha relación es llamado soluciones.
Los valores que satisfacen una ecuación es llamado soluciones, raíces o ceros. En una inecuación los valores de la variable que satisface a dicha relación es llamado soluciones.
Existe tres formas para expresar las soluciones de una inecuación y se da de forma:
- Analítica.
- Gráfica.
- Intervalos.
Analítica:$$x<2$$
Gráfica:

Intervalos:$$(k, \infty)\;;\;[k, \infty)\;;\;[k, l]$$
¿Cómo expresar las soluciones de las inecuaciones con desigualdades estrictas y no estrictas?
Las soluciones de una inecuación pueden expresarse mediante desigualdades estrictas ( < , > ), cuando el valor límite no se incluye en la solución, o mediante desigualdades no estrictas ( ≤ , ≥ ) cuando el valor límite sí forma parte de la solución.
Estas expresiones permiten indicar de forma precisa el conjunto de valores que cumplen la condición dada.
Desigualdades Estrictas
Cuando la solución analítica utiliza los signos menor que ( < ) o mayor que ( > ), el valor del extremo no está incluido.
En la solución gráfica se dibuja un círculo abierto (O) sobre el punto.
Para la solución de Intervalos se utilizan paréntesis ( , ) en los extremos.
Desigualdades No Estrictas
Cuando la solución analítica utiliza los signos menor o igual que (≤) o mayor o igual que (≥), el valor del extremo sí está incluido.
Para la gráfica se dibuja un círculo cerrado (o punto sólido) sobre el punto.
En el intervalo se utilizan corchetes [ , ] en los extremos incluidos.
Nota: El corchete y el paréntesis se combinan para intervalos mixtos, como [a, b), (a, b], o se usan solo corchetes para intervalos cerrados, [a, b].
Ejemplos de soluciones de inecuaciones según las desigualdades
Son cuatro situaciones que te ayudarán a comprender mejor la representación de las soluciones de las inecuaciones según los tipos de desigualdades (estrictas y no estrictas).
Situación#1
Analítica
$$x>k$$
La solución de la inecuación está formada por todos los números reales mayores que k.
Gráfica
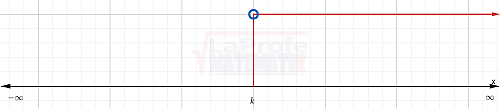
Para representar gráficamente la solución que incluye todos los valores mayores que k ( x > k ), se utiliza un círculo abierto (O) sobre el punto k (para indicar que k no está incluido) y se extiende con una flecha o sombreado hacia la derecha.
Intervalo
$$( k , \infty )$$
Se utilizan paréntesis ( a, b ) en ambos extremos para definir un intervalo abierto, lo cual indica que los valores de los extremos no están incluidos en la solución.
Situación#2
Analítica
$$x<k$$
La solución de la inecuación está formada por todos los números reales menores que k.
Gráfica
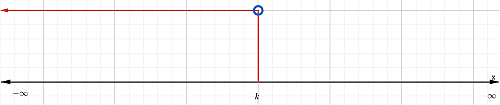
Para representar en la gráfica los valores menores que k (o x < k), se dibuja un círculo abierto (O) sobre el punto k y se traza una flecha o sombreado dirigido hacia la izquierda.
Intervalos
$$( – \infty, k )$$
Se utilizan paréntesis ( a, b ) en ambos extremos para definir un intervalo abierto. Esto significa que la solución está formada por todos los números reales menores que k:
- El símbolo −∞ indica que el intervalo se extiende indefinidamente hacia la izquierda.
- El paréntesis en k muestra que el valor k no está incluido en la solución.
Situación#3
Analítica
$$x \geq k$$
La desigualdad x ≥ k indica que el conjunto solución está formado por todos los números reales mayores o iguales a k.
Gráfica
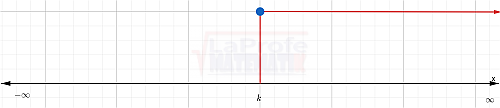
Para representar la solución gráfica de x ≥ k, se dibuja un círculo cerrado (o punto sólido) sobre el valor k (para indicar que k está incluido) y se extiende el sombreado o una flecha hacia la derecha.
Intervalos
$$[k, \infty )$$
Se expresa mediante:
- El corchete en k significa que el valor k está incluido.
- El paréntesis en ∞ indica que el intervalo se extiende indefinidamente y no incluye al infinito.
Situación#4
Analítica
$$x \leq k$$
La desigualdad x ≤ k indica que el conjunto solución está formado por todos los números reales menores o iguales a k.
Gráfica
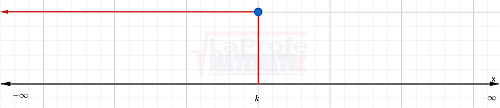
Se dibuja un círculo cerrado (o punto sólido) sobre el valor k (ya que está incluido) y se traza un sombreado o flecha que se dirige hacia la izquierda.
Intervalos
$$( -\infty , k ]$$
Significado:
- El paréntesis en −∞ indica que el intervalo se extiende indefinidamente hacia la izquierda.
- El corchete en k significa que el valor k está incluido en la solución.
Intervalos
 Un intervalo es un subconjunto del conjunto de los números reales (ℜ) que incluye todos los valores comprendidos entre dos extremos. Gráficamente, se representan sobre la recta numérica como un segmento o una semirrecta.
Un intervalo es un subconjunto del conjunto de los números reales (ℜ) que incluye todos los valores comprendidos entre dos extremos. Gráficamente, se representan sobre la recta numérica como un segmento o una semirrecta.
Existen dos tipos principales de intervalos:
Intervalos Acotados: Son aquellos que tienen dos extremos definidos por números reales y, por lo tanto, tienen un principio y un fin. Gráficamente, se representan como un segmento.
Intervalos No Acotados: Son aquellos que se extienden indefinidamente hacia el infinito positivo (+∞) o el infinito negativo (−∞). Gráficamente, se representan como una semirrecta o la recta real completa.
Notación y clasificación de intervalos en la recta real
 La representación de un conjunto de números reales en la recta numérica se realiza a través de los intervalos.
La representación de un conjunto de números reales en la recta numérica se realiza a través de los intervalos.
Aquí aprenderás su notación (paréntesis o corchetes), su clasificación (acotados o no acotados) y su traducción gráfica, elementos esenciales para resolver cualquier tipo de inecuación.
Intervalos No Acotados
[ k , +∞ )
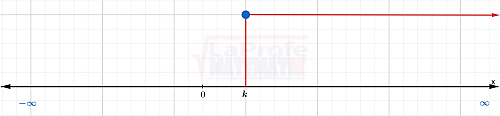
Intervalo infinito a la derecha.
( k , +∞ )
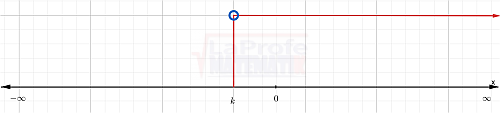
Intervalo infinito a la derecha sin incluir el extremo.
( -∞ , k ]
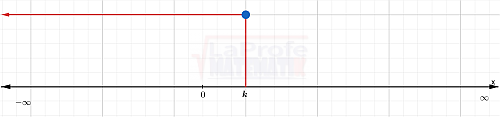
Intervalo infinito por la izquierda.
( -∞ , k )
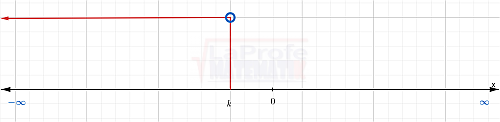
Intervalo infinito por la izquierda sin incluir el extremo.
( -∞ , ∞ )
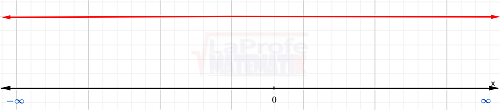
Intervalos infinitos por la izquierda y derecha.
Llamado también:
Para todo valor real ℜ.
Intervalos Acotados
( k , l )
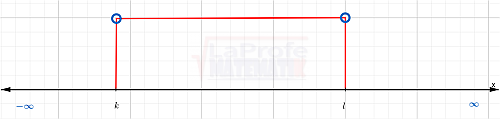
Intervalo abierto.
[ k , l )
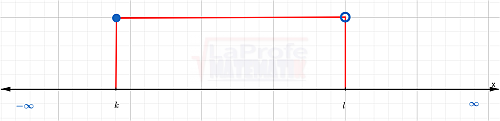
Intervalo semiabierto por la derecha.
( k, l ]
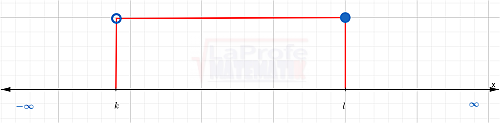
Intervalo semiabierto por la izquierda.
[ k , l ]
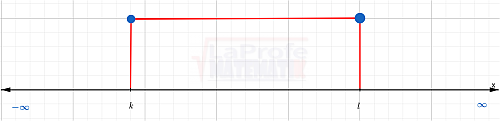
Intervalo cerrado
Inecuaciones lineales
Las inecuaciones lineales son el tipo más sencillo de desigualdades. Se caracterizan por tener un grado de exponente uno x1 en sus variables y se resuelven de manera muy similar a las ecuaciones de primer grado, usando las operaciones básicas (suma, resta, multiplicación y división).
El objetivo es despejar la incógnita para encontrar el conjunto de valores que satisfacen la desigualdad, en lugar de un único punto de solución.
Ejemplo # 1: Determinar la inecuación lineal
$$4x-\frac{1}{3}\leq 3x+\frac{1}{6}$$
Solución
$$4x-\frac{1}{3}\leq 3x+\frac{1}{6}$$
$$4x-3x\leq \frac{1}{6}+\frac{1}{3}$$
$$x\leq \frac{1}{2}$$
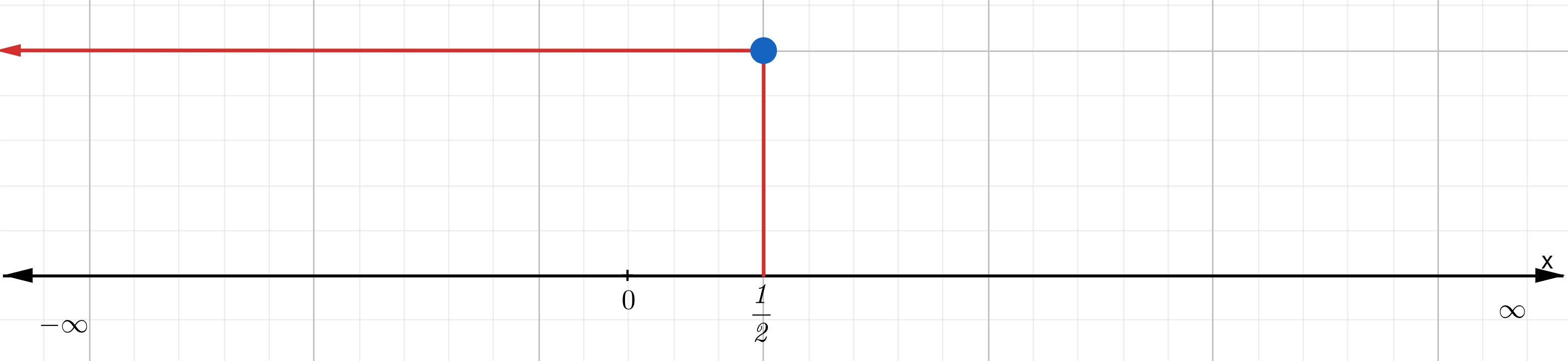
$$\left ( -\infty ,\frac{1}{2} \right )$$
Ejemplo # 2: Calcular la inecuación lineal
$$\frac{9x-5}{4}+3< \frac{7x+1}{3}+1$$
Solución
$$\frac{9x-5}{4}+3< \frac{7x+1}{3}+1$$
$$\frac{9x-5}{4}-\frac{7x+1}{3}< -3+1$$
$$\frac{3(9x-5)-4(7x+1)}{12}< -2$$
$$27x-15-28x-4< -24$$
$$-x-19< -24$$
$$-x< -5$$
$$x> 5$$
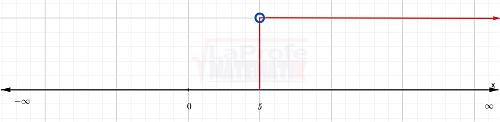
$$\left ( 5,\infty \right )$$
Sistema de inecuaciones lineales
Un sistema de inecuaciones está formado por dos o más desigualdades que deben resolverse de manera simultánea. El objetivo es encontrar el valor o el conjunto de valores de «x» que satisfacen a cada una de las inecuaciones. Para hallar la solución final, se resuelve cada inecuación por separado y, posteriormente, se analiza la intersección de los intervalos obtenidos (generalmente mediante una gráfica). Esta intersección representa las soluciones comunes a todas las desigualdades del sistema.
Ejemplo # 1: Resolver el sistema de inecuación lineal
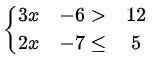
Solución
1° Inecuación
$$3x-6> 12$$
$$3x> 12+6$$
$$3x> 18$$
$$x> \frac{18}{3}$$
$$x> 6$$
Intervalo abierto: ( 6 , ∞ )
2° Inecuación
$$2x-7> 5$$
$$2x> 5-7$$
$$2x> -2$$
$$x> -\frac{2}{2}$$
$$x\leq -1 6$$
Intervalo infinito a la izquierda: ( -∞ , -1 ]
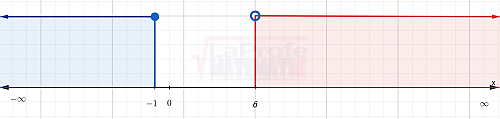
Solución común no existe, por lo tanto es:
S = Ø
Ejemplo # 2: Determinar el siguiente sistema de inecuación lineal
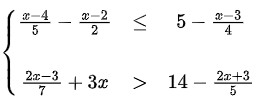
Solución
1° Inecuación
$$\frac{x-4}{5}-\frac{x-2}{2}\leq 5-\frac{x-3}{4}$$
$$\frac{x-4}{5}-\frac{x-2}{2}+\frac{x-3}{4}\leq 5$$
$$\frac{4(x-4)-10(x-2)+5(x-3)}{20}\leq 5$$
$$4x-16-10x+20+5x-15\leq 100$$
$$-x-11\leq 100$$
$$x\geq -111$$
Intervalo infinito a la derecha: [ -111 , ∞ )
2° Inecuación
$$\frac{2x-3}{7}+3x> 14-\frac{2x+3}{5}$$
$$\frac{2x-3}{7}+3x+\frac{2x+3}{5}> 14$$
$$10x-30+105x+14x+21>490$$
$$129x-9>490$$
$$129x> 499$$
$$x> \frac{499}{129}$$
$$\frac{499}{129}\approx 3,86$$
Intervalo infinito a la derecha sin incluir el extremo: $$\left ( \frac{499}{129},\infty \right )$$
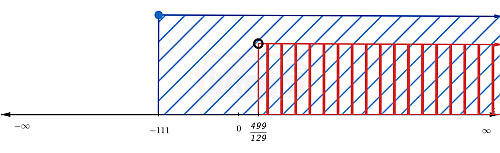
Si existe intersección es decir solución común:$$ S=\left ( \frac{499}{129},\infty \right )$$
Ejemplo # 3: Solucionar el sistema de inecuación lineal
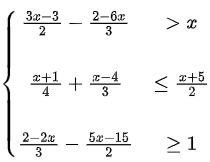
Solución
1° Inecuación
$$\frac{3x-3}{2}-\frac{2-6x}{3}> x$$
$$\frac{3x-3}{2}-\frac{2-6x}{3}-x> 0$$
$$\frac{3(3x-3)-2(2-6x)-6x}{6}> 0$$
$$9x-9-4+12x-6x> 0$$
$$15x-13> 0$$
$$15x> 13$$
$$x> \frac{13}{15}$$
$$\frac{13}{15}\approx 0,87$$
$$x>0,87$$
Intervalo infinito a la derecha: ( 13/15 , ∞ )
2° Inecuación
$$\frac{x+1}{4}+\frac{x-4}{3}\leq \frac{x+5}{2}$$
$$\frac{x+1}{4}+\frac{x-4}{3}-\left ( \frac{x+5}{2} \right )\leq 0$$
$$\frac{3(x+1)+4(x-4)-6(x+5)}{12}\leq 0$$
$$3x+3+4x-16-6x-30\leq 0$$
$$x-43\leq 0$$
$$x\leq43 $$
Intervalo infinito a la izquierda: (-∞ , 43]
3° Inecuación
$$\frac{2-2x}{3}-\frac{5x-15}{2}\geq 1$$
$$\frac{2(2-2x)-3(5x-15)}{6}\geq 1$$
$$4-4x-15x+45\geq 6$$
$$-19x+49\geq 6$$
$$-19x\geq 6-49$$
$$-19x\geq -43$$
$$19x\leq 43$$
$$x\leq \frac{43}{19}$$
$$\frac{43}{19}\approx 2,26$$
$$x\leq 2,26$$
Intervalo infinito a la izquierda: ( -∞ , 43/19 ]
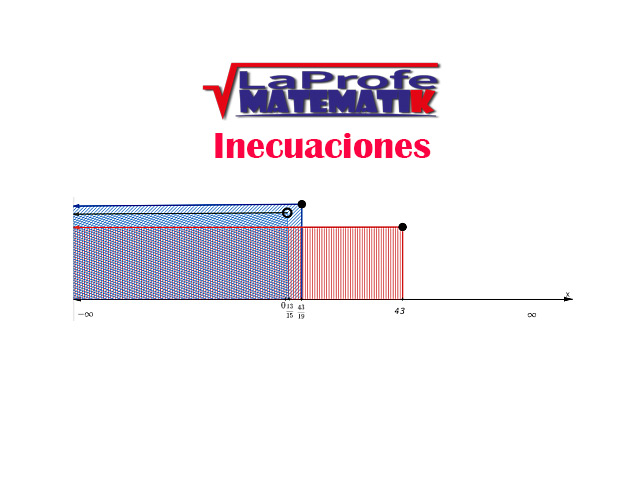
Gráfica
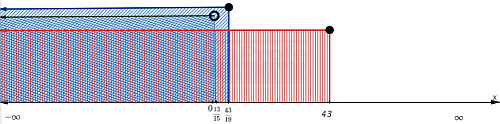
Existe intersección: ( -∞ , 13/15 )
Inecuaciones con valor absoluto
Las inecuaciones con valor absoluto representan un caso especial de las desigualdades, ya que exigen que la distancia de una expresión a cero cumpla con ciertas restricciones. Resolver estas inecuaciones requiere transformar la expresión inicial en dos o más desigualdades simples, eliminando el valor absoluto y analizando tanto el caso positivo como el caso negativo, para finalmente encontrar el conjunto de valores que satisfacen la condición.
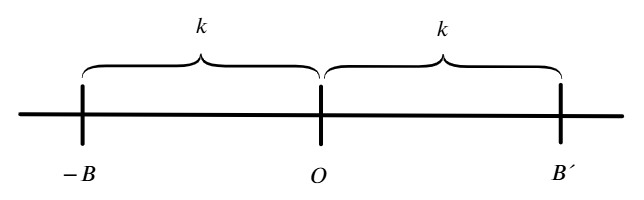
“ k ” es un número real, el valor absoluto de “ k ” es el valor positivo del mismo, se escribe | k | y se lee: valor absoluto de “ k ”.
La distancia ![]() y
y ![]() poseen la misma distancia que es igual a k, por lo tanto el valor absoluto puede definirse como la distancia
poseen la misma distancia que es igual a k, por lo tanto el valor absoluto puede definirse como la distancia ![]() =
= ![]()
El valor absoluto de una cantidad es calculado como se muestra:
| k | = k k > 0
| k | = –k k < 0
Ejemplo:
![]()
![]()
Los valores que satisfacen la ecuación elemental | x | = k es
x = k y x = –k
Es lo mismo decir: x = ± k
Mira el siguiente ejemplo: Resolver la siguiente ecuación | x | = 10
El resultado es: x = ± 10
La ecuación elemental | x | = k también es aplicable a expresiones polinómicas, como por ejemplo la siguiente:
![]()
Forma de presentación de las inecuaciones con valor absoluto
Las inecuaciones con valor absoluto puede presentarse de dos formas.
- Forma # 1: Es cuando | Q(x) | < k . Este tipo de forma su desigualdad es el signo < o ≤ , y representa un sistema. Por ser un sistema su solución pertenece a una intersección de los conjuntos solución. Su expresión sería:
![]()
![]()
![]()
- Forma # 2: Es cuando
 . Este tipo de forma su desigualdad es el signo > o ≥ , y no representa un sistema es una agrupación. Por ser un agrupación su solución pertenece a una unión de los conjuntos solución. Su expresión sería:
. Este tipo de forma su desigualdad es el signo > o ≥ , y no representa un sistema es una agrupación. Por ser un agrupación su solución pertenece a una unión de los conjuntos solución. Su expresión sería:
![]()
![]()
Ejemplo # 1: Resolver la inecuación con valor absoluto
$$|6 – x| < 13$$
Solución
Observa que pertenece a la forma # 1 y por lo tanto la solución será una intersección.
$$|6 – x| < 13$$
$$-6 – 13 < -x < 13 – 6$$
$$-19 < -x < 7$$
$$19 > x > -7$$
Gráfica
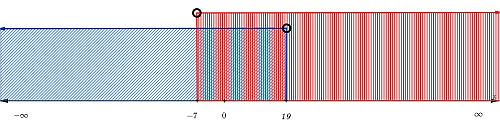
Intervalo
$$\left ( -7,19 \right )$$
Ejemplo # 2: Determinar la inecuación con valor absoluto
$$\left|\frac{6 – 4x}{5}\right| > 15$$
Solución
Pertenece a la forma # 2 y por lo tanto la solución será una unión.
$$\left|\frac{6 – 4x}{5}\right| > 15$$
$$-15 > \frac{6 – 4x}{5} > 15$$
$$-75 > 6 – 4x > 75$$
$$-6 – 75 > -4x > 75 – 6$$
$$-81 > -4x > 69$$
$$81 < 4x < -69$$
$$\frac{81}{4} < x < \frac{-69}{4}$$
$$\frac{81}{4} = 20,25$$
$$\frac{-69}{4} = -17,25$$
$$20,25 < x < -17,25$$
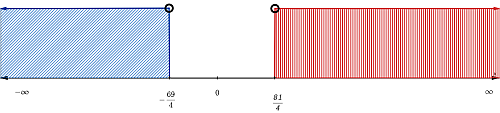
Intervalo
$$(-\infty, -\tfrac{69}{4}) \cup \left(\tfrac{81}{4}, \infty\right)$$
Gráfica
Inecuaciones racionales
Las inecuaciones raciones son desigualdades que poseen un polinomio en el numerador y otro en el denominador. La forma es la siguiente:$$\frac{P(x)}{Q(x)} > 0 \quad \land \quad \frac{P(x)}{Q(x)} < 0$$
![]()
Ambos polinomios son de exponentes enteros y positivos
La solución pertenece a una intersección de los conjuntos solución o parte en común entre ellos.
Ejemplo # 1: Solucionar la inecuación racional
$$\frac{4}{3x – 8} > 0$$
Solución
Según la expresión, la fracción tiene que ser positiva el numerador también lo es, esto quiere decir que el denominador debe ser positivo para que la fracción lo sea.
$$3x – 8 > 0$$
$$3x > 8$$
$$x > \frac{8}{3}$$
Intervalo
$$\left(\tfrac{8}{3}, \infty\right)$$
Gráfica

Ejemplo # 2: Resolver la inecuación racional
$$\frac{4x – 7}{x – 2} > 0$$
Solución
Según la expresión, la fracción debe ser positiva, por lo tanto es necesario que el numerador y el denominador tengan el mismo signo, observa:
Numerador y denominador > 0
$$4x – 7 > 0$$
$$4x > 7$$
$$x > \tfrac{7}{4}$$
$$x – 2 > 0$$
$$x > 2$$
Intervalo
$$(2, \infty)$$
Gráfica
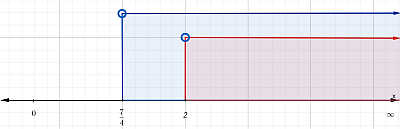
Numerador y denominador < 0
$$4x – 7 < 0$$
$$4x < 7$$
$$x < \tfrac{7}{4}$$
$$x – 2 < 0$$
$$x < 2$$
Intervalo
$$(-\infty, \tfrac{7}{4})$$
Gráfica
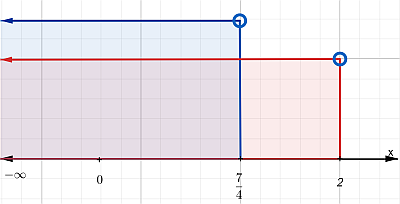
Solución
$$(2, \infty) \cup (-\infty, \tfrac{7}{4})$$
Ejemplo # 3: Calcular la inecuación racional
Determine la solución de la siguiente inecuación.
$$\frac{5x – 3}{3x + 2} < 0$$
Solución
La fracción debe ser negativa; por lo tanto, es indispensable que el numerador y el denominador tengan signos diferentes. En otras palabras, uno debe ser positivo y el otro negativo. Observa el siguiente caso:
Numerador > 0 y Denominador < 0
$$5x – 3 > 0$$
$$5x > 3$$
$$x > \frac{3}{5}$$
$$3x + 2 < 0$$
$$3x < -2$$
$$x < \frac{-2}{3}$$
Intervalo
No existe parte común
S = Ø
Gráfica
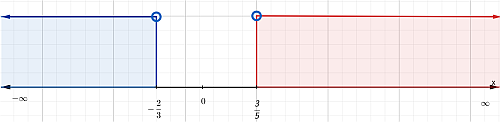
Numerador < 0 y denominador > 0
$$5x – 3 < 0$$
$$5x < 3$$
$$x < \frac{3}{5}$$
$$3x + 2 > 0$$
$$3x > -2$$
$$x > \frac{-2}{3}$$
Intervalo
$$\left( -\tfrac{2}{3}, \tfrac{3}{5} \right)$$
Gráfica
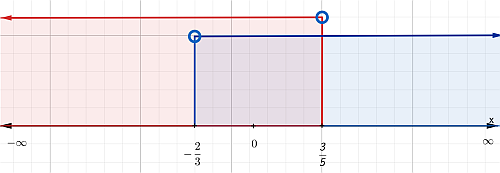
Solución
$$\left( -\frac{2}{3}, \frac{3}{5} \right)$$
Actividades
Resolver:
$$x + 11 < 23$$
$$5x – 3 \leq 6$$
$$7x + 5 \geq 8$$
$$9x + 11 > -2$$
$$5x + 4 < 4x + 9$$
$$10x + 13 \geq 8x – 5$$
$$\frac{3x – 6}{9} \leq 5$$
$$\frac{x}{2} + \frac{1}{4} < -5$$
$$\frac{2x + 1}{5} + 4 > \frac{x – 7}{9} – 11$$
$$5x + \frac{1}{7} \geq \frac{4x – 15}{8}$$
$$2x – 9 < 9x + 8$$
$$(x – 3)^2 + 7 \leq (x + 1)^2 – 5$$
$$3(x – 4) + 9 – 2x \geq 4(3x – 1) + 6(x + 3)$$
$$(x – 2)^3 < x^3 – 2(3x + 1)(x – 5)$$
$$x – 6 \geq 22$$
$$\frac{x}{2} + \frac{x}{3} – \frac{x}{4} < 7$$
$$\frac{x+4}{3} – \frac{x-4}{5} \leq 2 + \frac{3x-1}{15}$$
$$\tfrac{1}{2} \left[ x – \left( 1 + \tfrac{25}{26} \right) \right] – \tfrac{2}{13}(1 – 3x) > x$$
$$(x+1)^2 > [6 – (1-x)]x – 2$$
$$\tfrac{1}{4}\left(x – \tfrac{1}{5}\right) + \tfrac{1}{2}\left(x – \tfrac{1}{3}\right) \geq \tfrac{1}{3}\left(x – \tfrac{1}{4}\right)$$
$$\tfrac{x}{2} + \tfrac{x}{3} – \tfrac{x}{4} < 7$$
$$\tfrac{x+4}{3} – \tfrac{x-4}{5} \leq 2 + \tfrac{3x-1}{15}$$
$$\tfrac{1}{2} \left[ x – \left( 1 + \tfrac{25}{26} \right) \right] – \tfrac{2}{13}(1 – 3x) > x$$
$$(x+1)^2 > [6 – (1-x)]x – 2$$
$$(5x – 2)^2 – (3x + 1)^2 \geq (4x + 5)^2$$
$$x + 5 > 3$$
Resuelva los siguientes sistemas de inecuaciones:

Resuelva:
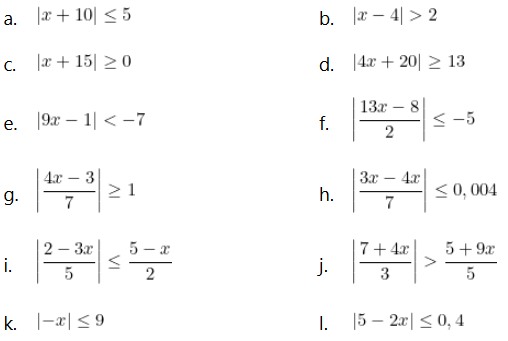
Determinar:

buenos días. quisiera consultar el programa donde realizo sus gráficos
Hola Xiomara, gusto en saludarte. El programa que utilizamos se llama GeoGebra. Saludos.