Si quieres aprender los números enteros con simulaciones interactivas has llegado al lugar indicado. Los números enteros son de gran utilidad en nuestra vida cotidiana y están presentes en muchos aspectos de nuestras vidas.
A continuación, te presentaré dos ejemplos prácticos.
El primero es cuando una persona solicita un extracto bancario: al revisar el informe, puede identificar los depósitos fácilmente porque aparecen como cantidades positivas, mientras que los retiros figuran como cantidades negativas.
El segundo ejemplo sucede cuando la misma persona se dirige a un elevador; al entrar observa que el panel de control los pisos están representados con números enteros positivos y negativos, indicando los niveles por encima y por debajo del suelo.
Definición
| Es el conjunto de números denominado Z, formados por enteros positivos, enteros negativos y el número cero. Donde el cero es un entero que no es negativo ni positivo. |
Subconjuntos notables en Z
El conjunto Ζ está formado por 3 subconjuntos denominados: subconjuntos notables, ellos son:
I.- El conjunto de los enteros positivos, conocidos como Ζ+:
Ζ+{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,…}
II.- El conjunto de los enteros negativos, conocidos como Ζ– :
Ζ– ={…,-9,-8,-7,-6,-5,-4,-3,-2,-1}
III.- El conjunto de todos los números enteros sin el 0, denotado como Ζ*:
Ζ* {…,-6,-5,-4,-3,-2,-1,1,2,3,4,5,6,…}
De esta forma se cumple que:
| Ζ+⊂ Ζ | Ζ–⊂ Ζ | Ζ*⊂ Ζ |
y
| Ζ = Ζ– ∪ {0} ∪ Ζ+ |
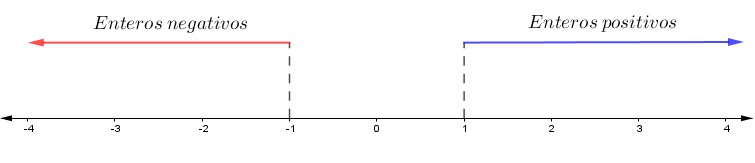
Números enteros en la recta numérica
El conjunto de los números Ζ en la recta numérica es relevante ya que permite:
I. Visualizar la posición.
II. Apreciar el orden de los números, facilitando la comparación y la comprensión de operaciones matemáticas básica como la suma y la resta.
Representación en la recta numérica
Para representar los números enteros en una la recta numérica debes cumplir con el siguiente procedimiento:
I. Dibujar una recta.
II. En la mitad de la recta, marca un punto para ubicar el número cero.
III. Crea una escala uniforme, por ejemplo de 1 en 1, 2 en 2, 5 en 5 dependiendo de la situación.
IV. A la derecha ubica los enteros positivos.
V. A la izquierda ubica los enteros negativos.
Números enteros opuestos
Al ubicar los números enteros en la recta numérica, podrás identificar fácilmente pares de números opuestos. Cada par está formado por un número a la derecha del cero (0) y su opuesto a la izquierda, ambos equidistantes del origen.
Se dice que dos números enteros son opuestos sólo si equidistan de cero y poseen diferentes signos.
Valor absoluto
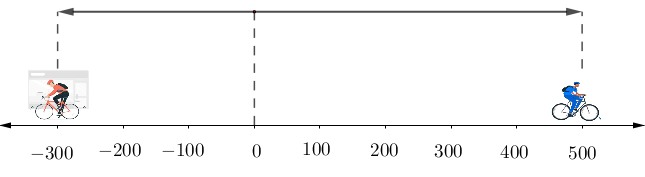
Dos ciclistas parten del origen; el de azul se dirige hacia el este y el de rojo hacia el oeste. En un instante dado, se encuentran a 500 m y 300 m del origen, respectivamente. Estas posiciones se representan como +500m y −300m, según la dirección de su movimiento. El ciclista azul recorrió 500 m y el ciclista rojo 300 m. Por lo tanto, 500 m y 300 m corresponden a los valores absolutos de +500m y −300m, ya que el valor absoluto refleja únicamente la magnitud del desplazamiento, sin considerar la dirección.
El valor absoluto es la distancia medida desde el cero de la recta numérica a cualquier entero positivo o negativo. Se representa por medio de dos barras verticales llamadas barras de valor absoluto. Si a ∈ Ζ, el valor absoluto de a se escribe así: |a|.
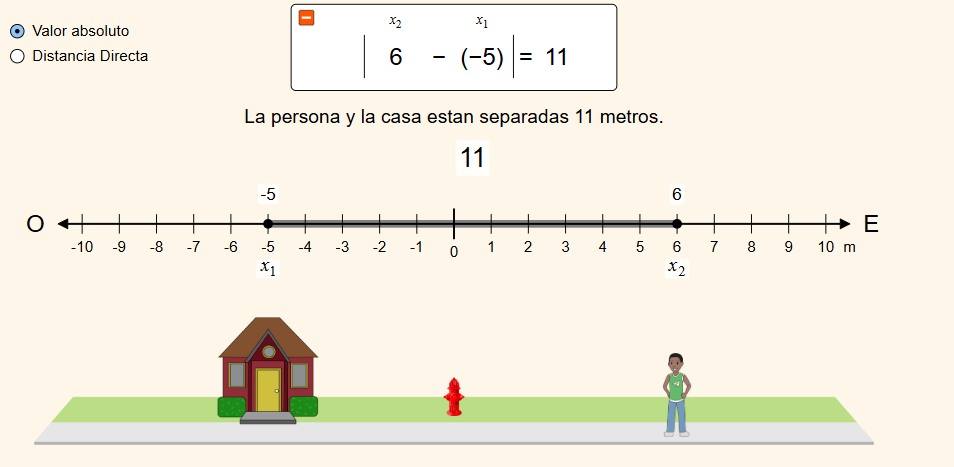
La imagen a continuación, muestra un ejemplo del valor absoluto entre una persona y una casa.
Es importante señalar que el valor absoluto de cero es cero, ya que no existe distancia alguna desde el origen. Su representación es: |0| = 0.
A jugar con valor absoluto
En esta simulación interactiva explorarás el concepto de valor absoluto a través de tres escenarios dinámicos.
Primero. La separación entre una casa y una persona. 
Segundo. Diferencia de temperatura. 
Tercero. La distancia vertical entre un pez y un ave. 
Aprenderás a medir distancias en una recta numérica, comprenderás cómo el valor absoluto representa la distancia de un número al cero.
Cuéntanos al final del post en comentarios qué escenario te pareció más fácil o más difícil.
Orden y comparación de números enteros
Al comparar dos números enteros siempre se cumple las siguientes relaciones:
> Mayor qué.
< Menor qué.
= Igual a.
La primera ventaja al configurar una recta numérica con números enteros es facilitar la identificación de cuál número es mayor o menor. El entero que esté más a la derecha es el mayor, mientras que el que esté más a la izquierda es el menor.
Observa las siguientes ilustraciones:
Sucede que: a > b, también se puede expresar como b < a
- a < b o b > a
- a = b
Ejemplo
Grafica sobre la recta numérica los siguientes números enteros: -1, 4, -6, 2 y 5.
¿Cuál de los números -6 y -1 está más a la derecha?
El -1 está más a la derecha que -6.
Entonces, -1 > -6 o -6 < -1
¿Qué número está más a la derecha el 5 o el 2?
El número 5 está más cercano a la derecha.
Por lo tanto, 5 > 2 o 2 < 5
Ordena de mayor a menor
+5, +4, +2, -1, -6
A jugar con: Orden y Comparación números enteros
En esta simulación interactiva aprenderás a comparar números utilizando signos como mayor que (>), menor que (<) e igual (=).
Te invitamos a dejar tu comentario abajo. Cuéntanos qué aprendiste, qué te gustó más o si te surgió alguna duda. ¡Tu opinión es muy importante para nosotros!
Operaciones con números enteros
Al realizar operaciones básicas con números enteros, es necesario conocer ciertas reglas y procedimientos debido a la presencia de números negativos.
Adición de dos números enteros de igual signo
Observa la imagen y saca tus propias conclusiones.
¿Cuántas fichas guardó un jugador en su bolsa?
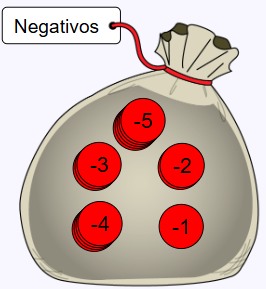
Respuesta:
Guardó -15 fichas.
Antes que veas la definición de la adición de dos números enteros de igual signo, es importante que sepas que en cualquier situación que involucre desplazamientos dirigidos hacia el este, o al oeste deben sumarse porque marchan hacia una misma dirección.
Lee con atención los siguientes escenarios:
Escenario # 1:
| David sale de su colegio, camina 3 km hacia al este, luego se detiene por unos minutos para revisar su celular y posteriormente avanza 1 km hacia el este. ¿A qué distancia llegó David respecto a su colegio? |
Observa en la recta numérica como David avanza +3 km y +1 km al este, el se dirige en la misma dirección, por lo tanto hay que sumar ambos desplazamientos.
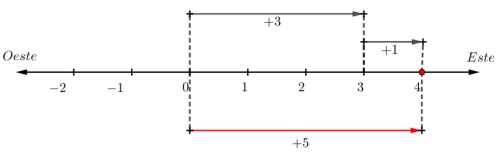
Entonces, David está a 4km de su colegio.
(+3) + (+1) = |+3| + |+1| = 3 + 1 = +4
Escenario # 2:
| Daniel sale de su casa en bicicleta y recorre 2 km hacia el oeste. Luego, hace una pausa para descansar y tomar agua. Después de unos minutos, continúa su trayecto y avanza otros 3 km en la misma dirección. ¿A qué distancia se encuentra ahora de su casa? |
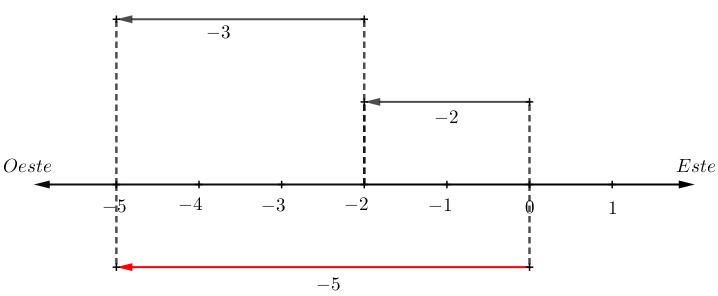
Observa, aquí Daniel se moviliza con su bicicleta 2 km al oeste y después avanza 3 km en la misma dirección, lo que quiere decir que hay que sumar ambos desplazamientos.
Entonces Daniel está localizado a 5km de su casa.
(-2) + (-3) = |-2| + |-3| = 2 + 3 = 5
Pero a la respuesta se le antepone el signo negativo, quedando de la siguiente forma:
(-2) + (-3) = -5
Definición de dos números enteros
| Para efectuar la adición de dos números enteros de igual signo, se suman los valores absolutos y el resultado se le antepone el mismo signo. |
Ejemplo. Efectúe las siguientes sumas sin hacer uso de la recta numérica:
(+5) + (+3) =
(-3) + (-6) =
Solución.
Se saca el valor absoluto de cada número entero.
|+5| = 5 ; |+3| = 3 ; |-3| = 3 ; |-6| = 6
Se opera anteponiendo el mismo signo
5 + 3 = +8
3 + 6 = +9
Adición de dos números enteros de distintos signos
Observa la imagen, un jugador introduce dos fichas rojas y dos amarillas, de acuerdo con la figura, el puntaje total se obtiene mediante la expresión:
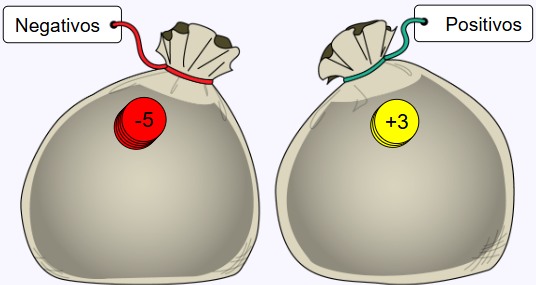
(-5) + 3 = -2
Definición de dos números enteros de distintos signos
| Es restar sus valores absolutos y la respuesta se le antepone el signo del número con mayor valor absoluto. |
Por ejemplo, (-10) + 8, se determinan los valores absolutos así:
(-10) + 8 = -2
¿Por qué?
Debes aplicarle valor absoluto a cada cantidad:
|-10| + |8|= 10 – 8 = 2
Pero a la respuesta se le antepone el signo negativo porque -10 es el número de mayor valor absoluto.
Propiedades de la adición de números enteros
En la adición de números enteros existen cinco propiedades, ellas son las siguientes:
Clausurativa. Llamada también propiedad cerrada ya que al sumar números enteros el resultado queda encerrado en el conjunto de los números enteros. Ejemplo:
(-4) + 3 = -1
-1 ∈ Ζ
Conmutativa. El orden de los sumandos no altera el resultado. Ejemplo:
(-8) + (-2) = (-2) + (-8)= -10
Asociativa. No importan como se agrupa tres o más números el resultado es el mismo.
[(-3) + 4] + 5 = (-3) + [ 4 +5 ] = 6
Elemento neutro. El cero es el elemento neutro de la suma ya que no cambia el valor del número con el que suma.
(-12) + (0) = -12
Inverso aditivo u opuesto. Al sumar el inverso del número el resultado siempre es cero.
(-4) + 4 = 0
(-6) + 6 = 0
Números enteros con simulaciones interactivas: A jugar sumando números enteros
Ahora que ya conoces cómo sumar números enteros con distintos e iguales signos, es el momento de desafiar tus conocimientos. Ingresa y cuéntanos en comentarios al final de este post.
Sustracción de números enteros
La sustracción m – n = o, m es el minuendo, n el sustraendo y o es llamada diferencia.
Es la suma el minuendo con el opuesto del sustraendo. Es decir, m – n = m + (-n).
Ejemplo: Resolver la siguiente sustracción: (-12) – 4 =
(-12) + ( 4) = – 8
Observa que se expresó la resta como una adición entre el minuendo, -12 y el opuesto del sustraendo, -4.
Ejemplos
Determinar el minuendo, el sustraendo y la diferencia de:
I. (-10) – 12
Minuendo = -10
Sustraendo = 12
Para obtener la diferencia se saca el opuesto del sustraendo que es -12
(-10) + (-12) = -22
La diferencia es -22
II. 18 – 25
Minuendo = 18
Sustraendo = 25
Para obtener la diferencia se saca el opuesto del sustraendo que es -25
18 + (-25) = -7
Multiplicación de números enteros
Existen momentos donde todos los sumandos son iguales, precisamente allí es oportuno usar la multiplicación, ya que ayuda a simplificar la expresión y generar una respuesta mucho más rápida, por ejemplo:
7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 70
10 x 7 = 70
En una multiplicación de números enteros m x n = o, donde m y n son llamados factores y o producto.
Al multiplicar números enteros se debe tener en cuenta la ley de los signos de la multiplicación, y es la siguiente:
( + ) ⋅ ( + ) = ( + )
( + ) ⋅ ( – ) = ( – )
( – ) ⋅ ( + ) = ( – )
( – ) ⋅ ( – ) = ( + )
Ejemplos
Resuelva las siguientes multiplicaciones.
(-4) × (+10) = -40
Observa que el producto es negativo por ser una multiplicación, allí se aplicó la ley de los signos (menos por más) generando un signo negativo.
(+8) × (+4) = +32
Ambos factores son positivos, por lo tanto su producto es positivo.
(-9) × (-2) = +18
Son factores que poseen el mismo signo negativo, resultando un producto positivo según la ley de signos.
Propiedades de la multiplicación
Las propiedades de la multiplicación de números enteros es la siguiente:
| Propiedad | Observación | Ejemplo |
| Clausurativa | m y n , el producto de m x n | (-3) x (9) = -27 = -27 |
| Conmutativa | m y n se cumple m x n = n x m | (-1) x (-2) = (-2) x (-1)= +2 |
| Asociativa | m, n, o se cumple (m x n) x o = m x (n x o) | [(-3) x 4] x 5 = (-3) x [ 4 x 5 ] = -60 |
| Neutro | El elemento neutro de la multiplicación es 1 | -5 x 1 = -5 |
| Elemento nulo | El elemento nulo de la multiplicación es cero 0 | -2 x 0 = 0 |
| Distributiva | m, n, o se cumple m x (n o) = m x nm x o | (-5) x (2 – 3) = (-5) x (2) + (-5) x (-3)= (-10)+(-15) = (-10) – 15 = -25 |
División de números enteros
El resultado de una división de números enteros no siempre resulta otro entero. En este post solo se considerará la división de dos números enteros resultando otro entero.
La expresión para dividir dos números enteros puede darse de dos maneras:
m ÷ n
$$\frac{m}{n}$$
Al dividir números enteros debes considerar la ley de los signos de la división, que es la siguiente:
( + ) ÷ ( + ) = ( + )
( + ) ÷ ( – ) = ( – )
( – ) ÷ ( + ) = ( – )
( – ) ÷ ( – ) = ( + )
Ejemplos
Resuelva las siguientes divisiones.
( -4 ) ÷ ( +2 ) = -2
El cociente es negativo por la ley de signos.
$$\frac{-10}{-2}=+5$$
El resultado es positivo por la ley de los signos.
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
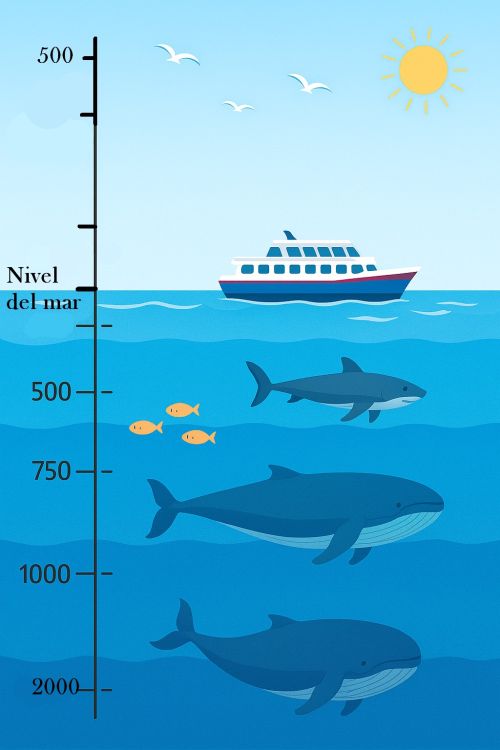
I. La escala que se muestra en la imagen a continuación está expresada en metros.
- ¿A qué altura se encuentra el ave más grande?
- ¿Qué profundidad aproximada tienen los peces?
- El tiburón lleva 500m de profundidad y la ballena 750m ¿Qué diferencia de altura existe?
- ¿Qué distancia tiene la ballena más grande?
II. Analiza
- ¿Qué número entero existe a 4 unidades a la izquierda de -2?
- ¿Qué números enteros están entre -8 y -3?
- ¿Cuántos números enteros hay entre 5 y -5?
- ¿Qué número entero se encuentra 8 unidades a la derecha de -4?
III. Determinar el valor absoluto de los números enteros que representan la ubicación del ave y del tiburón, sabiendo que el nivel del mar es cero 0. Vea la figura océano.
IV. Crea una recta numérica y grafica los siguientes números enteros: -9, 7, -4, 10, 2. Luego ordénalos de mayor a menor.
V. Escribe el opuesto de los siguientes números enteros: -4, -6, 9, 12, 8.
VI. Ordena, de menor a mayor, cada grupo de números:
- -4, 2, 25, 0, -9, -13.
- 34, 5, -56, 13, 12, 6, -1.
VII. Completa cada expresión con los signos menor que “<”, mayor que “>” o igual “=”
- 5 ___-10
- -3___ 5
- |-3|___3
- |-6|___|-4|
VIII. Resuelve cada operación.
- (-72)/(-6)=
- 396/(-11)=
- (-135)/9=
- 0/-4=
IX. Responde verdadero o falso las siguientes afirmaciones:
- El cociente de una división exacta es positivo, si el dividendo es negativo y el divisor negativo
- En una división cuando el cociente es 0, es porque el divisor es cero.
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión