 ¿Quieres saber más de dominio, asíntotas y gráficas? Si es así, has llegado al sitio indicado. La siguiente colección de 10 ejercicios te invita a dominar el análisis de funciones racionales, una habilidad clave que va mucho más allá del aula. Al resolverlos, no solo adquirirás la destreza para identificar dominios y asíntotas, sino que también desarrollarás una capacidad de pensamiento crítico aplicable en diversas áreas.
¿Quieres saber más de dominio, asíntotas y gráficas? Si es así, has llegado al sitio indicado. La siguiente colección de 10 ejercicios te invita a dominar el análisis de funciones racionales, una habilidad clave que va mucho más allá del aula. Al resolverlos, no solo adquirirás la destreza para identificar dominios y asíntotas, sino que también desarrollarás una capacidad de pensamiento crítico aplicable en diversas áreas.
Entender estas funciones te permitirá interpretar datos en la economía para predecir tendencias de mercado, en la ingeniería para diseñar sistemas eficientes, e incluso en la ciencia para modelar fenómenos biológicos. Esta práctica te equipará con las herramientas necesarias para descifrar la complejidad de nuestro entorno, transformando un concepto matemático abstracto en una poderosa herramienta para la toma de decisiones y la solución de problemas en la vida real.
Funciones racionales
Las funciones racionales están compuesta por la división de dos polinomios. Su forma general es:
$$f(x)=\frac{R(x)}{S(x)}$$
Donde R(x) y S(x) son polinomios, y S(x) ≠ 0.
Consideraciones para el análisis
Para analizar una función racional, es fundamental centrarse en dos aspectos: su dominio y el comportamiento de sus asíntotas. Estos elementos son esenciales para comprender tanto los puntos de discontinuidad de la función como su comportamiento a largo plazo.
Dominio
El dominio de una función racional son todos los números reales, a excepción de valores que convierten al denominador S(x) a cero.
Asíntotas
Según los grados de los polinomios R(x) y S(x), una función racional puede poseer asíntotas las cuales son rectas imaginarias que actúan como guías o límites en el comportamiento de la función.
Existen tres tipos de asíntotas: verticales, horizontales y oblicuas.
Una función racional puede poseer:
- Varias asíntotas verticales de acuerdo con las raíces reales del denominador.
- Una asíntota horizontal y varias verticales, cuando el grado del numerador es menor o igual al del denominador.
- Una asíntota oblicua y varias verticales, cuando el grado del numerador es exactamente uno más que el del denominador.
Asíntotas verticales
Las asíntotas verticales son rectas que actúan como barreras o límites indicando los valores de x para los cuales la función no está definida, es decir, los valores que no pertenecen a su dominio. Esto ocurre cuando el denominador de una función racional se anula. Su forma es x = a .
Asíntotas horizontales
Una asíntota horizontal es una recta imaginaria de la forma y = b que describe el comportamiento a largo plazo de una función. La curva de la función se aproxima a esta recta a medida que los valores de x se hacen extremadamente grandes o pequeños ( x → ∞ o x → -∞ ).
A diferencia de las asíntotas verticales que son barreras estrictas, la asíntota horizontal no es una limitación para toda la función. La curva puede cruzarla en algún punto, pero a medida que se aleja del origen, la distancia entre la función y la asíntota tiende a cero.
Este tipo de asíntota es esencialmente el límite de la función en el infinito, lo cual expresa hacia qué valor constante se dirige la función en sus extremos.
Por ejemplo, si una función tiene una asíntota horizontal en y = 4, significa que a medida que x se mueve hacia ∞ o –∞, la curva se acerca más a la recta y = 4.
Una función racional tendrá asíntota horizontal cuando cumpla con alguno de los siguientes casos:
Caso # 1: Cuando el grado del numerador < grado del denominador.
En este caso, cuando 𝑥 → ± ∞, 𝑓 ( 𝑥 ) → 0
Así que la asíntota es horizontal es la recta:
$$y=0$$
Caso # 2: Cuando el grado del numerador = grado del denominador.
La asíntota horizontal es la razón entre los coeficientes principales.
$$y=\frac{a_{n}}{b_{n}}$$
Asíntotas oblicuas
Es una recta imaginaria de la forma y = mx + b ( m ≠ 0 ) donde la curva de la función se aproxima a medida que los valores de x se hacen muy grandes o muy pequeños ( x ±∞ ).
A diferencia de las asíntotas horizontales, que indica que la función se estabiliza en un valor constante, la asíntota oblicua describe el comportamiento a largo plazo en el que la función crece o decrece indefinidamente, llevando una trayectoria diagonal o inclinada.
Como ocurre con las asíntotas horizontales la curva de la función puede cruzar su asíntota oblicua en algún punto.
Identificar la asíntota oblicua en una función racional es muy fácil sólo debe cumplir que:
$$f(x)=\frac{R(x)}{S(x)}=\frac{ax^{n+1}}{bx}$$
Para obtener la asíntota debes dividir el polinomio del numerador entre el polinomio del denominador siendo el cociente la asíntota oblicua.
Intersecciones con los ejes
Los puntos donde la función cruza el eje x (raíces) y el eje y.
Comportamiento cerca de la asíntota vertical
Para conocer el comportamiento de la función a medida que se acerca a sus asíntotas verticales.
Comportamiento a largo plazo
Es el estudio de los límites de la función, lo cual permite conocer hacia dónde tiende la gráfica cuando 𝑥 crece sin límite o disminuye indefinidamente.
Rango
El rango es el conjunto de todos los valores de “y” que la función puede tomar.
Tabla de valores
Con algunos puntos estratégicos permite graficar la función, ayudando a verificar el comportamiento que se ha analizado teóricamente.
Ejercicios racionales resueltos
A continuación, te presento 10 ejercicios de funciones racionales resueltos paso a paso. En cada uno, podrás ver la aplicación de los conceptos anteriores, como el cálculo del dominio, la identificación de asíntotas, el análisis de su comportamiento para comprender la forma de la gráfica, entre otros.
Ejercicio 1
$$f(x)=\frac{1}{x-3}$$
Solución
1. Dominio
El denominador es x, y debe ser distinto a cero:
$$x-3≠0 ⇒ x≠3$$
Como el denominador es diferente a 3, el dominio es:
$$\boxed{D_{f}=(-\infty,3 )\cup (3,\infty )}$$
2. Intersecciones
- Eje «x» y = 0
$$0=\frac{1}{x-3}\Rightarrow 0\neq 1$$
No tiene solución.
No hay intersección con el eje X
- Eje «y» x = 0
$$y=\frac{1}{0-3}$$
$$y=-\frac{1}{3}$$
$$\boxed{A\left ( 0,-\frac{1}{3} \right )}$$
3. Cálculo de las asíntotas
Esta función posee dos asíntotas ellas son:
Vertical
$$x-3=0$$
$$\boxed{x=3}$$
Horizontal
Se cumple que: n < m
Posee una asíntota horizontal en el eje “x”
$$\boxed{y=0}$$
Oblicua
No existe asíntota oblicua.
4. Comportamiento cerca de la asíntota vertical
$$\boxed{x=3}$$
Valores por la izquierda
$$x=2,9 \Rightarrow f(2,9)=\frac{1}{2,9-3}=-10$$
Entonces,
$$x\to 3^{-} f(x)\to-\infty$$
Conclusión: Al acercarse por la izquierda a 3, la función crece negativamente.
Valores por la derecha
Entonces,
$$x\to 3^{+} f(x)\to+\infty$$
Conclusión: Al acercarse por la derecha a 3, la función crece positivamente.
5. Comportamiento a largo plazo
Valores por la izquierda
$$f(-100)=\frac{1}{-100-3}\approx-0,0097$$
$$f(-1000)=\frac{1}{-1000-3}\approx-0,00099$$
Conclusión: Al reemplazar valores negativos cada vez más pequeños, la función se acerca a 0
$$f(x)\to 0 $$
Valores por la derecha
$$f(-100)=\frac{1}{-100-3}\approx-0,010$$
$$f(-1000)=\frac{1}{-1000-3}\approx-0,001$$
Conclusión: Al sustituir valores positivos cada vez mucho mayor, la función se acerca a 0
$$f(x)\to 0 $$
6. Cálculo del rango
$$y=\frac{1}{x-3}\Rightarrow y(x-3)=1$$
$$yx-3y=1$$
$$x=\frac{1+3y}{y}$$
$$\boxed{\mathbb{R}_{f}=\left ( -\infty,0 \right )\cup \left ( 0,\infty \right )}$$
| Gráfica |
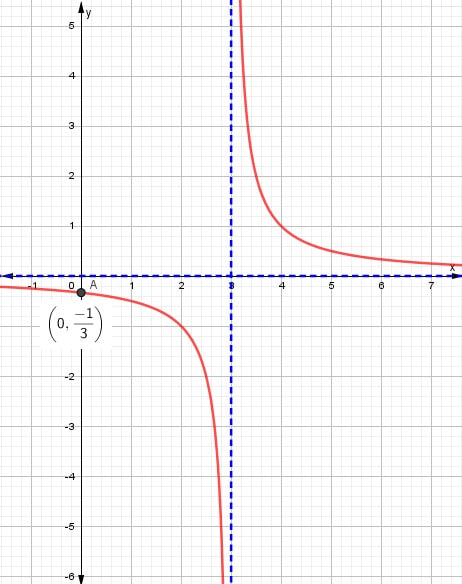 |
ResumenFunción: \( f(x) = \frac{1}{x – 3} \)
|
Ejercicio 2
$$f(x)=\frac{x}{x+2}$$
1. Dominio
El denominador debe ser diferente de cero.
$$x+2≠0 ⇒ x≠-2$$
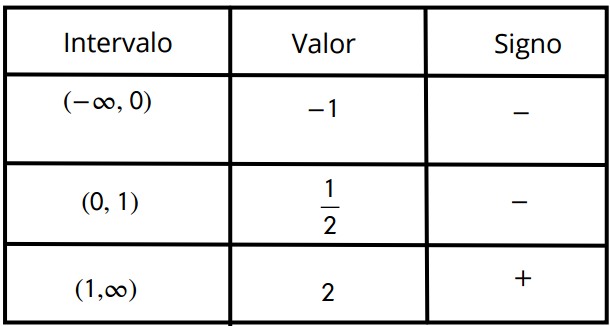
Se realiza un estudio del signo de la función:
Numerador:
$$x=0$$
Denominador:
$$x=-2$$
| Intervalo | Valor | Signo |
| $$\left ( -\infty , -2 \right )$$ | -3 | + |
| $$\left ( -2 , 0 \right )$$ | 1 | – |
| $$\left ( 0, \infty \right )$$ | 1 | + |
Entonces, el dominio es:
$$\boxed{\mathbb{D}_{f}=\left ( -\infty,-2 \right )\cup \left ( -2,\infty \right )}$$
2. Intersecciones
- Eje «x» y = 0
$$0=\frac{x}{x+2}\Rightarrow x=0$$
$$\boxed{A(0,0)}$$
- Eje «y» x = 0
$$y=\frac{0}{0+2}$$
$$y=0$$
$$\boxed{B(0,0)}$$
3. Cálculo de las asíntotas
Esta función posee dos asíntotas ellas son:
Vertical
$$x+2=0$$
$$\boxed{x=-2}$$
Horizontal
Se cumple que:
n = m, la función f posee una asíntota horizontal y es la recta horizontal
$$\boxed{y=1}$$
Oblicua
No existe asíntota oblicua.
4. Comportamiento cerca de la asíntota vertical
$$\boxed{x=-2}$$
Valores por la izquierda
Entonces,
$$x\to -2^{-} f(x)\to\infty$$
Conclusión: Al aproximarse por la izquierda a -2, la función crece positivamente.
Valores por la derecha
Entonces,
$$x\to -2^{+} f(x)\to-\infty$$
Conclusión: Al aproximarse por la derecha a -2, la función disminuye negativamente.
5. Comportamiento a largo plazo
Valores por la izquierda
$$f(-100)=\frac{-100}{-100+2}\approx1,0204$$
$$f(-1000)=\frac{-1000}{-1000+2}\approx1,002$$
Conclusión: Al reemplazar valores negativos cada vez más pequeños, la función se acerca a 1
$$f(x)\to 1 $$
Valores por la derecha
$$f(100)=\frac{100}{100+2}\approx0,980$$
$$f(1000)=\frac{1000}{1000+2}\approx0,998$$
Conclusión: Al dar valores positivos cada vez mucho mayor, la función se acerca a 1
$$f(x)\to 1 $$
6. Cálculo del rango
$$y=\frac{x}{x+2}\Rightarrow y(x+2)=x$$
$$yx+2y=x$$
$$yx-x=-2y$$
$$x(y-1)=-2y$$
$$x=\frac{-2y}{y-1}$$
$$y≠1$$
$$\boxed{\mathbb{R}_{f}=\left ( -\infty,1 \right )\cup \left ( 1,\infty \right )}$$
ResumenFunción: \( f(x) = \frac{x}{x + 2} \)
|
| Gráfica |
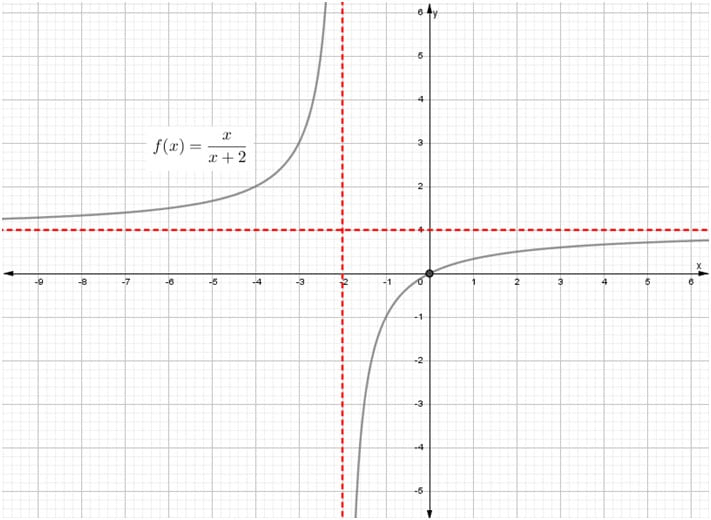 |
Ejercicio 3
$$\text{Sea } f(x) = \frac{2x + 1}{x – 4}$$
Solución:
El denominador debe ser diferente de cero
$$x-4\neq 0\Rightarrow x\neq 4$$
Estudio del signo de la función
Numerador:
$$2x+1=0\Rightarrow -\frac{1}{2}$$
Denominador:
$$x=4$$
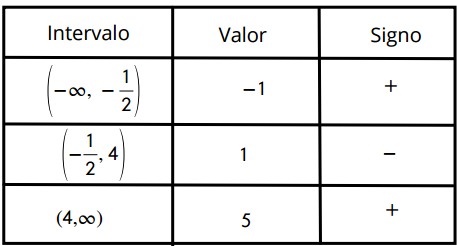
Dominio
$$D_{f}=(-\infty ,4)\cup (4,\infty )$$
Intersecciones
Con el eje “x” y = 0
$$0=\frac{2x+1}{x-4}\Rightarrow x=-\frac{1}{2}$$
$$A\left ( -\frac{1}{2},0 \right )$$
Con el eje “y” x = 0
$$y=\frac{2\cdot 0+1}{0-4}\Rightarrow y=-\frac{1}{4}$$
$$y=-\frac{1}{4}$$
$$B\left ( 0,-\frac{1}{4} \right )$$
Asíntotas
Vertical:
$$x-4=0$$
$$x=4$$
Horizontal:
Posee una asíntota horizontal y es la recta:
$$y=2$$
Oblicua:
No existe.
Comportamiento cerca de la asíntota vertical
$$x=4$$

Comportamiento a largo plazo

Rango
$$y=\frac{2x+1}{x-4}\Rightarrow y(x-4)=2x+1$$
$$yx-4y-2x=1$$
$$x(y-2)=1+4y$$
$$x=\frac{1+4y}{y-2}$$
$$y\neq 2$$
$$R_{f}=(-\infty,2)\cup(2,\infty)$$
| Gráfica |
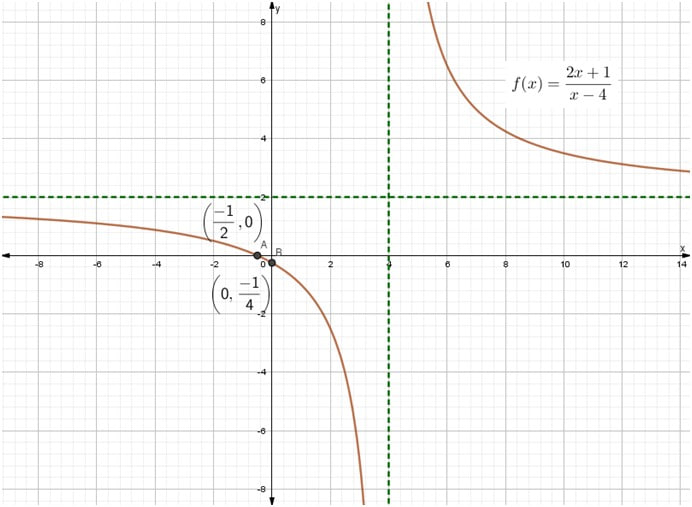 |
ResumenFunción: \( f(x) = \frac{2x+1}{x – 4} \)
|
Ejercicio 4
$$\text{Sea } f(x) = \frac{x^2}{x – 1}$$
Solución:
El denominador debe ser diferente de cero
$$x-1\neq 0\Rightarrow x\neq 1$$
Estudio del signo de la función
Numerador:
$$x^{2}=0\Rightarrow x=0$$
Denominador:
$$x=1$$
Dominio
$$D_{f}=\left ( -\infty ,1 \right )\cup \left ( 1,\infty \right )$$
Intersecciones
En el eje “x” ( y = 0)
$$y=\frac{x^{2}}{x-1}\Rightarrow x=0$$
$$A(0,0)$$
Eje “y” ( x = 0)
$$y=\frac{0^{2}}{0-1}\Rightarrow y=0$$
$$B(0,0)$$
Asíntotas
Vertical:
$$x-1=0$$
$$x=1$$
Horizontal:
No posee asíntota horizontal.
Oblicua:
Cumple con la condición, por tanto posee asíntota oblicua.
Dividir el polinomio del numerador entre el denominador:
$$x^{2}\div x-1=x+1$$
La asíntota oblicua es:
$$y=x+1$$
Comportamiento cerca de la asíntota vertical
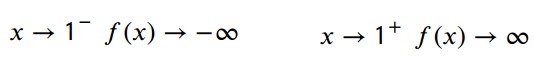
Comportamiento a largo plazo
![]()
Rango
$$y=\frac{x^{2}}{x-1}\Rightarrow y(x-1)=x^{2}$$
$$yx-y=x^{2}$$
$$x^{2}-yx+y=0$$
$$\Delta =b^{2}-4ac\geq 0$$
Donde:
a = 1 ; b = -y ; c = y
$$\Delta =(-y)^{2}-4(1)(y)=y^{2}-4y$$
$$y^{2}-4y\geq 0$$
$$y(y-4)\geq 0$$
Entonces:
y = 0
y = 4

$$R_{f}=(-\infty ,0]\cup [4,\infty )$$
| Gráfica |
 |
ResumenFunción: \( f(x) = \frac{2x+1}{x – 4} \)
|
Ejercicio 5
$$f(x) = \frac{x-5}{x^{2} – 25}$$
Solución
Factorización y simplificación
$$f(x)=\frac{1}{x+5}$$
Posee una discontinuidad removible en: x = 5
Coordenadas del hueco
$$f(5)=\frac{1}{5+5}=\frac{1}{10}$$
$$H\left ( 5,\frac{1}{10} \right )$$
Dominio
El denominador debe ser diferente de cero
$$x+5\neq 0\Rightarrow x\neq -5$$
$$D_{f}=(-\infty ,-5)\cup (-5,\infty )$$
Intersecciones
Eje “x” ( y = 0 )
$$0=\frac{1}{x+5}\Rightarrow 0\neq 1$$
No existe intersecciones con el eje “x”
Eje “y” ( x = 0 )
$$y=\frac{1}{0+5}$$
$$y=\frac{1}{5}$$
$$A\left ( 0,\frac{1}{5} \right )$$
Asíntotas
Vertical:
$$x+5=0$$
$$x=-5$$
Horizontal:
$$y=0$$
Oblicua:
No existe, no cumple con la condición.
Comportamiento cerca de la asíntota vertical
![]()
Comportamiento a largo plazo
$$f(x)\to 0$$
Rango
$$y=\frac{1}{x+5}\Rightarrow y(x+5)=1$$
$$yx+5y=1$$
$$x=\frac{1-5y}{y}$$
$$y\neq 0$$
$$R_{f}=(-\infty ,0)\cup (0,\infty )$$
| Gráfica |
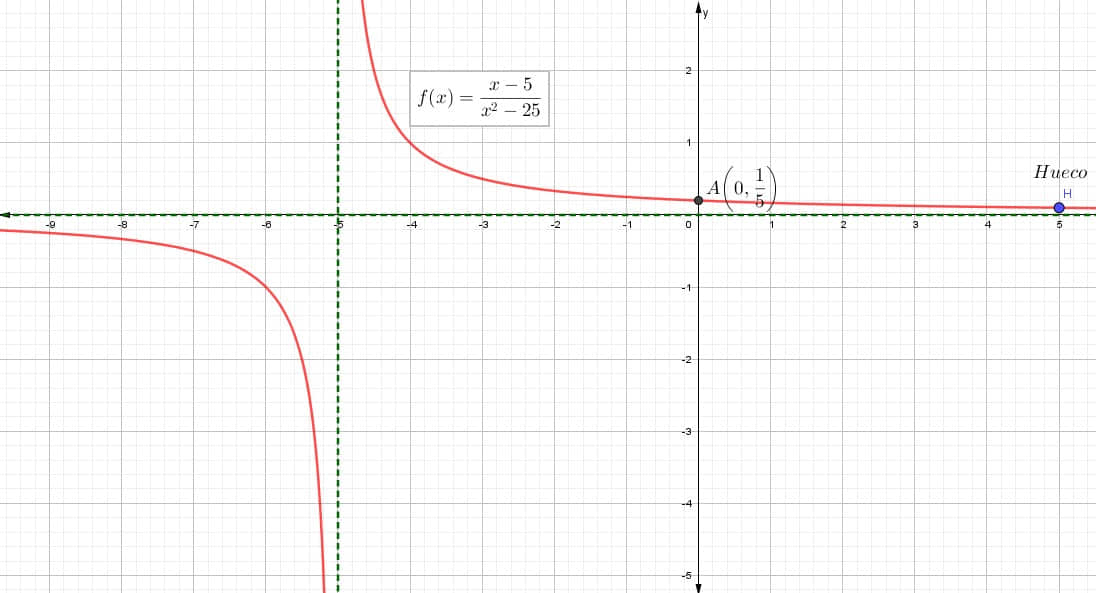 |
ResumenFunción: \( f(x) = \frac{x-5}{x^{2} – 25} \)
|
Ejercicio 6
$$f(x) = \frac{x+1}{x^{2} -3x+2}$$
Solución:
Factorización y simplificación
$$f(x)=\frac{x+1}{x^{2}+3x+2}$$
$$f(x)=\frac{x+1}{(x+1)(x+2)}$$
$$f(x)=\frac{1}{x+2}$$
Posee una discontinuidad removible en: x = -1
Coordenadas del hueco
$$f(-1)=\frac{1}{-1+2}=1$$
$$H\left ( -1,1 \right )$$
Dominio
El denominador debe ser ≠ de cero.
$$x+2\neq 0\Rightarrow x\neq -2$$
$$D_{f}=(-\infty ,-2)\cup (-2,\infty )$$
Intersecciones
Eje “x” ( y = 0 )
$$0=\frac{1}{x+2}\Rightarrow 0\neq 1$$
No existe intersecciones con el eje “x”
Eje “y” ( x = 0 )
$$y=\frac{1}{0+2}$$
$$y=\frac{1}{2}$$
$$A\left ( 0,\frac{1}{2} \right )$$
Asíntotas
Vertical:
$$x+2=0$$
$$x=-2$$
Horizontal:
$$y=0$$
Oblicua:
No existe, no cumple con la condición.
Comportamiento cerca de la asíntota vertical
Asíntota vertical:
$$x=2$$
![]()
Comportamiento a largo plazo
$$f(x)\to0$$
Rango
$$f(x)=\frac{1}{x+2}\Rightarrow y(x+2)=1$$
$$yx+2y=1$$
$$x=\frac{1-2y}{y}$$
$$y\neq 0$$
$$R_{f}=(-\infty ,0)\cup (0,\infty )$$
| Gráfica |
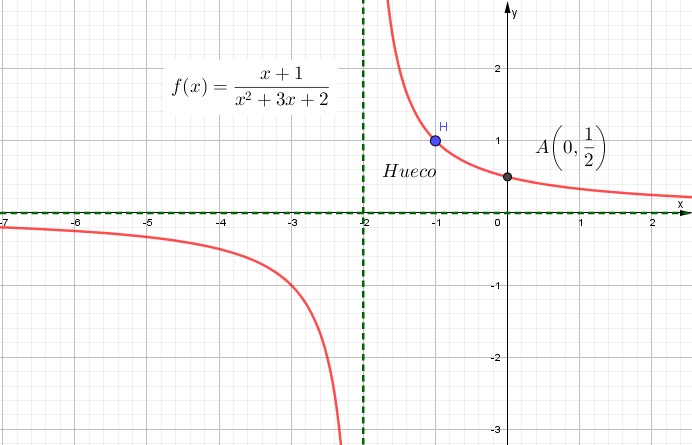 |
ResumenFunción: \( f(x) = \frac{x+1}{x^{2} +3x+2} \)
|
Ejercicio 7
$$f(x) = \frac{x^{2}-4}{x+2}$$
Solución:
Paso 1: Identificar posibles restricciones
El denominador no puede ser cero.
$$x+2=0\Rightarrow x=-2$$
Paso 2: Factorizar y simplificar
El numerador es una diferencia de cuadrados:
$$f(x)=\frac{x^{2}-4}{x+2}=\frac{(x-2)(x+2)}{(x+2)}$$
$$f(x)=x-2$$
Solo cuando $$x \neq -2$$
Entonces la función:
$$f(x)=x-2$$
Es una función lineal, pero con un hueco (discontinuidad removible) en x = -2
Paso 3: Coordenadas del hueco:
$$f(-2)=-2-2=-4$$
$$H\left ( -2,-4 \right )$$
Paso 4: Dominio
$$D_{f}=R-{-2}$$
Porque en x = -2 el denominador se anula y la función no está definida.
Paso 5: Intersecciones
Eje “x” ( y = 0 )
$$0=x-2\Rightarrow x=2$$
$$A( 2,0 )$$
Eje “y” ( x = 0 )
$$f(x)=0-2$$
$$y=-2$$
$$B(0,-2)$$
Paso 6: Asíntotas
Vertical:
No hay asíntota vertical, sino un hueco (discontinuidad removible) en x = -2
Horizontal:
Cuando el grado del numerador es mayor que el denominador, no hay asíntota horizontal.
Oblicua:
Si el grado del numerador es exactamente uno más que el denominador, existe una asíntota oblicua, esto quiere decir que sí existe una asíntota oblicua.
La función se comporta como una recta: $$y=x-2$$
Entonces, la función obtenida coincide con su asíntota oblicua en: $$y=x-2$$
Paso 7: Comportamiento cerca de la asíntota vertical
Como no existe asíntota vertical sino un hueco (discontinuidad removible) en x = -2, el comportamiento cerca de x = -2 no es de crecer a ±∞ sino que la recta se aproxima al punto (-2,-4) sin llegar a alcanzarlo.
Paso 8: Comportamiento a largo plazo
A largo plazo ( x → ±∞ ), la función tiende a su asíntota oblicua porque la diferencia entre ambas desaparece cuando x crece o decrece; en consecuencia, f(x) se comporta igual que la recta y = x -2.
Paso 9: Rango
Se realiza el despeje en la función dada:
$$y = \frac{x^2 – 4}{x+2}\Rightarrow$$
$$yx + 2y = x^2 – 4$$
$$x^2 – yx – (2y+4) = 0$$
Esta es una ecuación cuadrática en x, cuyo discriminante es:
$$\Delta = (-y)^2 – 4(1)(-(2y+4))$$
$$\Delta =y^2 + 8y + 16$$
$$\Delta = (y+4)^2$$
Observación:
Si el discriminante es:

Como el Δ calculado es:
$$\Delta =(y+4)^2$$
Y una expresión al cuadrado nunca es negativo, se concluye que:
$$(y+4)^2 \geq 0$$
Para todo y, por lo que siempre hay raíces reales o una doble raíz. Pero en este caso y = -4 donde el Δ = 0 y la única raíz es x = -2, que está excluida del dominio.
Por lo tanto el rango es:
![]()
| Gráfica |
 |
ResumenFunción: \( f(x) = \frac{x^{2}-4}{x+2} \)
|
Ejercicio 8
$$f(x) = \frac{3x^{2} + 2x-1}{x^{2} – 1}$$
Solución:
Paso 1: Factorizar simplificar y coordenadas del hueco
El numerador es una diferencia de cuadrados:
$$f(x) = \frac{3x^{2} + 2x-1}{x^{2} – 1}$$
$$f(x)=\frac{(3x-1)(x+1)}{(x+1)(x-1)}$$
$$f(x)=\frac{3x-1}{x-1}$$
Posee una discontinuidad removible en x = -1
Se reemplaza en valor de x = -1 determinar las coordenadas del hueco.
$$f(x)=\frac{3\cdot (-1)-1}{(-1)-1}=2$$
Coordenadas del hueco: $$H(-1,2)$$
Paso 2: Identificar posibles restricciones
El denominador debe ser distinto a cero.
$$x-1\neq 0\Rightarrow x\neq 1$$
Paso 3: Estudio del signo de la función:
Numerador:
$$3x-1=0\Rightarrow x=\frac{1}{3}$$
Denominador:
$$x=1$$
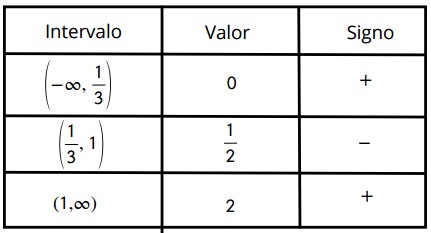
Dominio
$$D_{f}=(-\infty ,1)\cup (1,\infty )$$
Intersecciones
Con el eje “x” y = 0
$$0=\frac{3x-1}{x-1}\Rightarrow x=\frac{1}{3}$$
$$A\left ( \frac{1}{3},0 \right )$$
Con el eje “y” x = 0
$$y=\frac{3\cdot 0-1}{0-1}\Rightarrow y=1$$
$$B(0,1)$$
Asíntotas
Vertical:
$$x-1=0$$
$$x=1$$
Horizontal:
Posee una asíntota horizontal y es la recta:
$$y=3$$
Oblicua:
No existe.
Comportamiento cerca de la asíntota vertical
![]()
Comportamiento a largo plazo
![]()
Rango
$$y= \frac{3x^{2} + 2x-1}{x^{2} – 1}$$
$$y(x^{2}-1)=3x^{2}+2x-1$$
$$yx^{2}-y=3x^{2}+2x-1$$
$$yx^{2}-3x^{2}-2x-y+1=0$$
$$(y-3)x^{2}-2x-(y-1)=0$$
Discriminante (Δ)
a = y – 3; b = -2; c = -( y – 1 )
$$\Delta =b^{2}-4ac$$
$$\Delta =(-2)^{2}-4(y-3)(-(y-1))$$
$$\Delta =4+4(y-3)(y-1)$$
$$\Delta =4+4(y^{2}-4y+3)$$
$$\Delta =4y^{2}-16y+16$$
$$\Delta =4(y^{2}-4y+4)$$
$$\Delta =4(y-2)^{2}$$
En la ecuación cuadrática
$$(y-3)x^{2}-2x-(y-1)=0$$
$$ax^{2}+bx+c=0$$
El coeficiente de x2 es a= y – 3
Si y = 3, a = 0. Esto quiere decir que ya no es una cuadrática, sino una ecuación lineal en x:
$$-2x-(3-1)=-2x-2=0$$
$$x=-1$$
Pero x = -1 está prohibido en el dominio porque x2 – 1 = 0. Por lo tanto y = 3 no pertenece al rango.
![]()
| Gráfica |
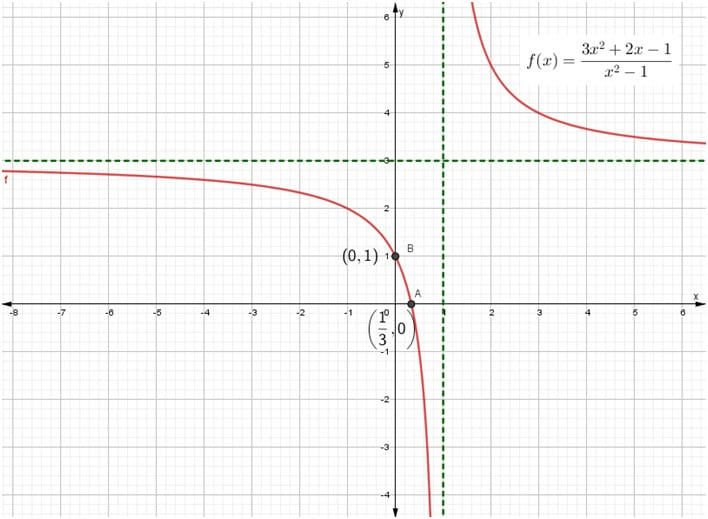 |
ResumenFunción: \( f(x) = \frac{3x^{2} + 2x-1}{x^{2} – 1} \)
|
Ejercicio 9
$$\text{Sea } f(x) = \frac{4}{x^{2} + 1}$$
Solución
Dominio
$$D_{f}=\mathbb{R}$$
Intersecciones
Con el eje “x” y = 0
$$0=\frac{4}{x^{2}+1}\Rightarrow 0\neq 4$$
No hay intersección con el eje “x”
Con el eje “y” x = 0
Asíntotas
Vertical:
No existe, ya que el denominador no se hace cero.
Horizontal:
$$y=0$$
Oblicua:
No existe.
Comportamiento cerca de una asíntota vertical
No existe asíntotas verticales ni huecos, la función está definida y es continua en todo R.
Comportamiento a largo plazo ( x → ±∞ )
$$f(x)\rightarrow 0$$
Rango
$$y=\frac{4}{x^{2}+1}$$
$$y(x^{2}+1)=4$$
$$x^{2}=\frac{4-y}{y}$$
Como x2 ≥0, se cumple que:
$$\frac{4-y}{y}\geq 0$$
Numerador: 4 – y ≥ 0 ⇒ y ≤ 4.
Denominador: y > 0 (porque está en el denominador original y además y = 0 no es posible, pues sería:
$$x^{2}+1=\infty $$
Entonces:
$$0< y\leq 4$$
$$R_{f}=(0,4]$$
| Gráfica |
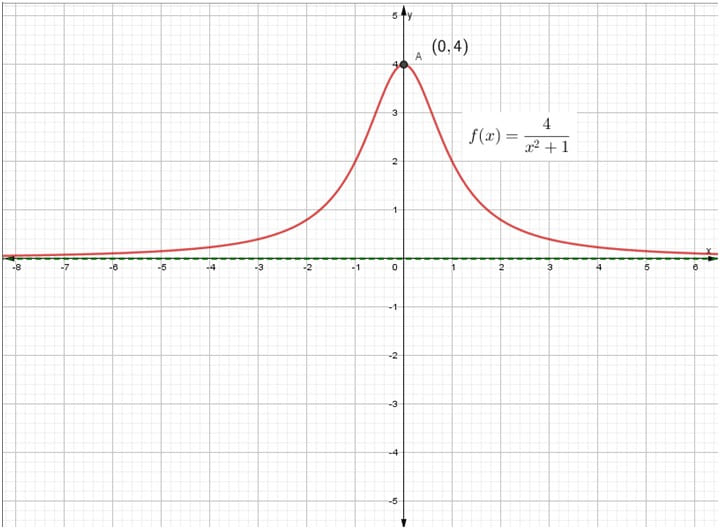 |
ResumenFunción: \( f(x) = \frac{4}{x^{2} + 1} \)
|
Ejercicio 10
$$f(x) = \frac{x^{2}+x-6}{x + 3}$$
Solución
Paso 1: Factorizar y simplificar
$$f(x)=x-2$$
Solo cuando $$x \neq -3$$
Entonces la función:
$$f(x)=x-2$$
Es una función lineal, pero con un hueco (discontinuidad removible) en x = -3
Paso 2: Coordenadas del hueco
$$f(-3)=-3-2=-5$$
$$H=\left ( -3,-5 \right )$$
Paso 3: Dominio
![]()
Paso 4: Intersecciones
Eje “x” ( y = 0 )
$$0=x-2\Rightarrow x=2$$
$$A( 2,0 )$$
Eje “y” ( x = 0 )
$$f(x)=0-2$$
$$y=-2$$
$$B(0,-2)$$
Paso 5: Asíntotas
Vertical:
No existe asíntota vertical, sino un hueco (discontinuidad removible) en x = -2
Horizontal:
No cumple con la condición, por tanto no existe asíntota horizontal.
Oblicua:
El grado del numerador es uno más que el denominador, entonces existe una asíntota oblicua que también coincide con la función.
Paso 6: Rango
$$y=\frac{x^{2}+x-6}{x+3}$$
$$y(x+3)=x^{2}+x-6$$
$$yx+3y=x^{2}+x-6$$
$$x^{2}+(1-y)x-(6+3y)=0$$
Discriminante
$$\Delta =(1-y)^{2}-4\cdot 1\cdot (-(6+3y))$$
$$\Delta =(1-y)^{2}+4(6+3y)$$
$$\Delta =y^{2}+10y$$
$$\Delta =(y+5)^{2}$$
Hay soluciones para todo y
$$(y+5)^{2}\geq 0$$
Única exclusión cuando Δ=0
$$y=-5$$
Al reemplazar este valor en la ecuación cuadrática
$$x^{2}+(1-y)x-(6+3y)=0$$
$$x^{2}+(1-(-5))x-(6+3(-5))=0$$
$$x^{2}+6x+9=0$$
Al resolver:
x = -3, pero este valor no pertenece al dominio, porque anula el denominador original.
Entonces el rango es:
![]()
| Gráfica |
 |
ResumenFunción: \(f(x) = \frac{x^{2}+x-6}{x + 3} \)
|
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
