Descubre el poder del Undecágono: precisión, arte y geometría en acción 🔺✨

Vota

¿Sabías que las figuras geométricas están presentes en casi todo lo que nos rodea? El undecágono regular, aunque poco común, se esconde en muchos lugares: en el diseño de logotipos, en patrones de mosaicos, en la estructura de algunos estadios o incluso en gráficos digitales de videojuegos. Comprender cómo se define y se construye esta figura no solo fortalece tus habilidades geométricas, sino que también te permite apreciar la precisión y belleza que la matemática aporta al arte, la tecnología y la vida cotidiana. En este post descubrirás qué es un undecágono regular y cómo construirlo paso a paso, usando tus instrumentos de geometría y además el software de GeoGebra, con la precisión de un verdadero diseñador.

Contenido del tema

Definición

El undecágono (también llamado endecágono) es un polígono de once lados y once vértices. Cuando todos sus lados y ángulos son congruentes, se denomina undecágono regular. Esta figura plana puede inscribirse en una circunferencia, o bien circunscribirse alrededor de ella, mostrando una perfecta simetría.

Características

Para comprender a fondo esta figura plana, es fundamental conocer elementos como el radio, el ángulo central, las diagonales y dominar el uso del compás y el transportador para construirla con precisión. Explorar el undecágono regular permite fortalecer habilidades de trazado, observación de simetrías y aplicación de relaciones trigonométricas en el diseño geométrico, desarrollando al mismo tiempo la creatividad y la exactitud propias del pensamiento matemático.

Las características de un undecágono son las siguientes:

Total de lados. $$n=11$$
El número de vértices es igual al número de lados.
Número de diagonales trazadas desde un mismo vértice.

$$d=n-3$$

$$d=11-3$$

$$d=8$$

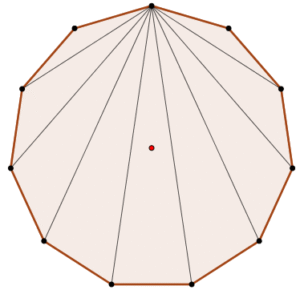
Total de diagonales.

$$D=\frac{n(n-3)}{2}$$

$$D=\frac{11(11-3)}{2}$$

$$D=\frac{88}{2}$$

$$D=44$$

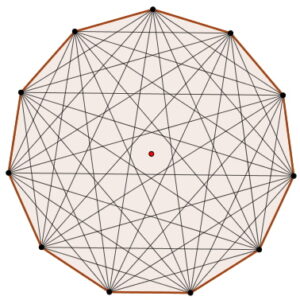
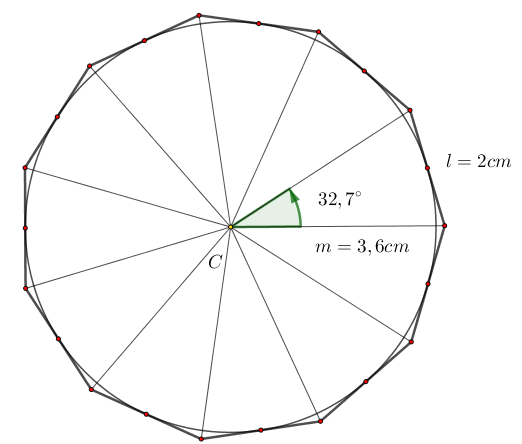
En un undecágono regular, ninguna diagonal pasa por el centro del polígono, ya que al tener un número impar de lados, no existen vértices opuestos. Observa la figura anterior.

Ángulo interno.

$$i=\frac{180^{\circ }\cdot (n-2)}{n}$$
$$i=\frac{180^{\circ }\cdot (11-2)}{11}$$
$$i=\frac{180^{\circ }\cdot 9}{11}$$
$$i=\frac{1620}{11}$$
$$i=147,27$$

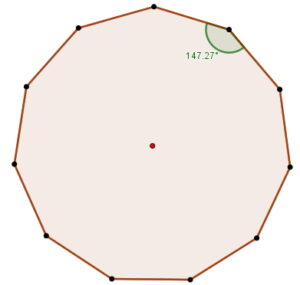
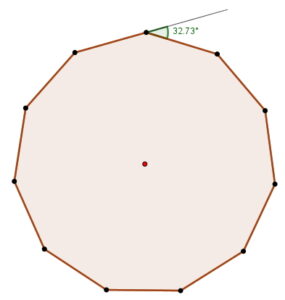
Ángulo exterior.

$$e=\frac{360^{\circ }}{11}$$
$$e=32,73^{\circ }$$

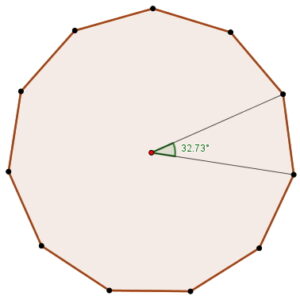
Ángulo central

$$\theta =\frac{360^{\circ }}{11}=32,73^{\circ }$$

$$\theta =32,73^{\circ }$$

Suma de ángulos internos.

$$S_{i}=180^{\circ }\cdot (n-2)$$
$$S_{i}=180^{\circ }\cdot (11-2)$$
$$S_{i}=180^{\circ }\cdot 9$$
$$s_{i}=1620^{\circ }$$

Suma de ángulos externos.

$$S_{e}=360^{\circ }$$

Formado por 11 triángulos isósceles

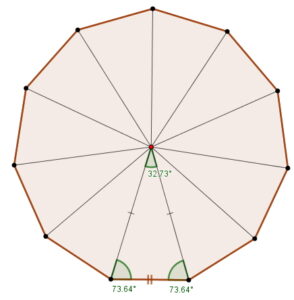
Perímetro. $$P=11\cdot n$$
Área. $$A=\frac{11\cdot l^{2}\cdot cot\left ( \frac{180^{\circ } }{11} \right )}{4}$$

Donde: l = lado.

Es un polígono convexo, ya que sus ángulos internos son menores de 180°.
Pueden ser inscritas en una circunferencia, y circunscribirse a otra.

Construcción de un decágono regular dado el valor de su lado (l)

Para construir un decágono regular conociendo la medida de su lado 𝑙, es necesario aplicar con precisión los pasos geométricos. A partir del valor del lado, se determina el radio del polígono regular mediante la ley del seno y utilizando el transportador y la regla. Esta construcción refuerza la comprensión de los ángulos centrales, la simetría y la importancia del trazado exacto en los polígonos regulares.

Ley del seno

$$\frac{m}{sen\beta }=\frac{l }{sen\alpha }$$
$$m=\frac{l\cdot sen\beta }{sen\alpha }$$
$$l=\frac{m\cdot sen\alpha }{sen\beta }$$

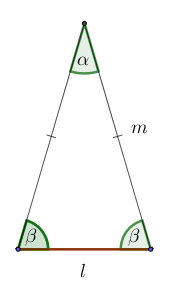Donde:

m = radio del polígono regular.

l = lado del polígono.

β = 73,6°

α =32,7°

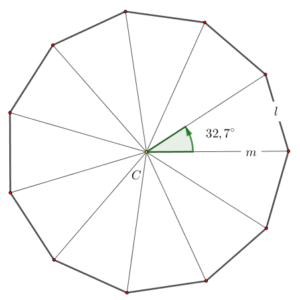
Procedimiento para la construcción.

Marcar el centro del polígono (C). Este punto será el vértice del ángulo central y el origen de todos los radios.

Calcular el radio del polígono regular (m). Aplicando la ley de Senos:$$m=\frac{l\cdot sen\beta }{sen\alpha }$$
Trazar el primer radio de la longitud (m) desde el punto (C).
Colocar el transportador con su centro sobre (C) y alinearlo con el radio trazado.
Marcar el primer ángulo central de 32,73°. Y dibujar el siguiente radio.
Repetir el proceso de marcar y trazar radios cada 32,73° hasta completar los 11 radios.
Unir los extremos consecutivos de los radios para formar los lados del undecágono regular.

Construcción de un undecágono regular inscrito en la circunferencia

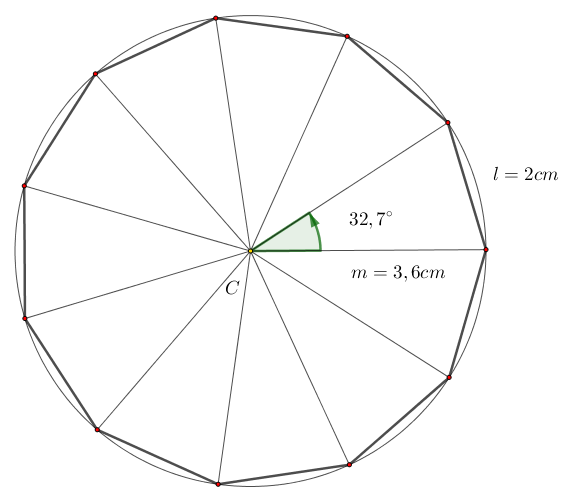
Para construir un undecágono regular inscrito en una circunferencia, es fundamental dominar el uso del compás, la regla y el transportador, ya que permiten trazar, medir y unir con precisión cada vértice. Con ayuda de la Ley del Seno determinas el radio del polígono, y al usar líneas finas y gruesas logras distinguir con claridad al polígono y a la circunferencia.

Ejemplo. Crear un undecágono de lado 2cm inscrito en una circunferencia.

Solución

Cuando el undecágono está inscrito en una circunferencia el radio de la circunferencia es igual al radio del polígono regular. Es decir:$$\frac{m}{sen\beta }=\frac{l }{sen\alpha }$$
$$r_{C}=r_{P}$$

Procedimiento:

Marcar un punto (C).
Calcular el radio del polígono regular (m). $$m=\frac{l\cdot sen\beta }{sen\alpha }$$

$$m=\frac{2cm\cdot sen73.63^{\circ } }{sen32,73^{\circ } }$$
$$m\approx 3,55cm$$

Aproximando a la décima queda así:
$$m=3,6cm$$

Graduar al compás al radio del polígono regular (m).
Apoyar la punta de metal del compás en el punto (C).
Girar y dibujar suavemente la circunferencia.
Trazar el radio del polígono regular (m) utilizando la regla con línea fina.
Construir el ángulo α = 32,7° utilizando el transportador y trazar el radio con línea fina.
Marcar un punto en la intersección.
Repetir los pasos 7 y 8 hasta completarlo.
Unir los puntos creados.

Construcción de un undecágono regular circunscrito en la circunferencia

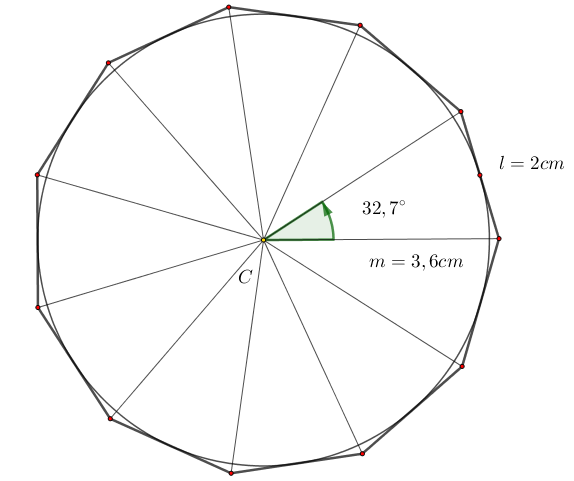
Para la construcción del undecágono regular circunscrito en una circunferencia, es esencial el buen manejo de los instrumentos, ya que permiten determinar los puntos de tangencia y trazar los lados del polígono con exactitud.

Ejemplo. Construir un undecágono de lado 2cm circunscrito en una circunferencia.

Solución

Cuando el undecágono es circunscrito el radio de la circunferencia es diferente al radio del polígono regular. $$r_{C}\neq r_{P}$$

Pasos:

Marcar el punto (C).
Calcular el radio del polígono regular (m). $$m=\frac{l\cdot sen\beta }{sen\alpha }$$

$$m=\frac{2cm\cdot sen73.63^{\circ } }{sen32,73^{\circ } }$$
$$m\approx 3,55cm$$

Aproximando a la décima queda así:
$$m=3,6cm$$

Trazar el radio del polígono regular (m) utilizando la regla con línea fina.
Construir el ángulo α = 32,7° utilizando el transportador y trazar el radio con línea fina.
Marcar un punto en la intersección.
Repetir los pasos 7 y 8 hasta completarlo.
Unir los puntos creados.
Determina el punto medio de cada lado del polígono y márcalos con un punto.
Coloca la punta del compás en el centro del polígono y ábrelo hasta alcanzar el punto medio de uno de los lados.
Traza la circunferencia con una línea delgada, manteniendo el compás fijo en el centro.

Construcción de un undecágono regular circunscrito e inscrito en una circunferencia utilizando GeoGebra

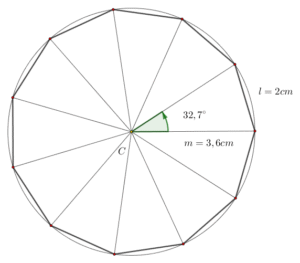
Con GeoGebra, construir un undecágono regular inscrito o circunscrito es una circunferencia es un proceso sencillo, preciso y rápido. Esta herramienta también facilita visualizar las relaciones geométricas entre el polígono y la circunferencia.

Ejemplo. Dibuja un undecágono de lado 2cm inscrito y circunscrito en una circunferencia utilizando el software de GeoGebra.

Solución

Herramientas a utilizar:

Punto
Segmento de longitud dada
Ángulo dada su amplitud
Segmento
Circunferencia (centro, punto)
Medio o Centro

Construcción del polígono inscrito en la circunferencia

Abrir GeoGebra.
Crear el centro del polígono (C) seleccionando la herramienta Punto.
Dibujar el radio del polígono usando la herramienta Segmento de longitud dada e ingresa el valor. Según la ley del seno$$m=3,6cm$$
Crear el ángulo de 32,7° utilizando la herramienta Ángulo dada su longitud e ingresa el valor del ángulo y selecciona el sentido antihorario o horario.
Dibuja el radio del polígono con línea fina, selecciona la herramienta Segmento.
Repetir los pasos 4 y 5 hasta completarlo.
Trazar todos los lados del polígono eligiendo la herramienta Segmento.
Dibujar la circunferencia seleccionando la herramienta Circunferencia (centro, punto), haciendo clic desde el centro (C) hasta el punto de intersección con la circunferencia.

Construcción del polígono circunscrito en la circunferencia

Abrir GeoGebra.
Crear el centro del polígono (C) seleccionando la herramienta Punto.
Dibujar el radio del polígono usando la herramienta Segmento de longitud dada e ingresa el valor. Según la ley del seno$$m=3,6cm$$
Crear el ángulo de 32,7° utilizando la herramienta Ángulo dada su longitud e ingresa el valor del ángulo y selecciona el sentido antihorario o horario.
Dibuja el radio del polígono con línea fina con la herramienta Segmento.
Repetir los pasos 4 y 5 hasta completarlo.
Trazar todos los lados del polígono eligiendo la herramienta Segmento.
Marcar los puntos medios de cada lado del polígono usando la usando la herramienta Medio o Centro y tocar esos lados para obtener el punto medio.
Dibujar la circunferencia seleccionando la herramienta Circunferencia (centro, punto), haciendo clic desde el centro (C) hasta el punto medio de cada lado.

Actividades

I.Construye:

Construir un undecágono de lado 4cm.
Dibujar en GeoGebra un undecágono regular con una radio del polígono de 8cm. ¿Cuál es el valor de sus lados?
Construye un undecágono circunscrito que tenga como lados una dimensión de 5cm.

II.Lee cuidadosamente cada afirmación y menciona Verdadero o Falso según corresponda.

El undecágono también se conoce con el nombre de endecágono. ___
El undecágono regular tiene once lados y once vértices iguales. ____
Todas las diagonales de un undecágono pasan por el centro del polígono. ___
En un polígono regular con número impar de lados no existen vértices opuestos. ___
El ángulo central de un undecágono se obtiene dividiendo 360° entre 11. ___
El radio del undecágono regular une el centro con uno de sus lados. ___
Para construir un undecágono regular, se puede inscribir en una circunferencia. ___
En un undecágono regular, todos los lados son congruentes. ___
La suma de los ángulos internos de un undecágono es igual a: $$S_{i}=180^{\circ }\cdot (n-5)$$
GeoGebra es una herramienta útil para construir un undecágono con precisión. ___