¿Alguna vez te has preguntado qué son exactamente las funciones elementales? En matemáticas, es muy común trabajar con estas funciones, también conocidas como funciones usuales. Son las piezas básicas con las que construimos todo. Al combinarlas a través de operaciones como la suma, resta, multiplicación y división, podemos crear funciones más complejas, llamadas funciones no elementales. Comprender estas funciones es el primer paso para dominar el cálculo.
Clasificación de las funciones elementales
 Las funciones elementales son los bloques de construcción básicos de las matemáticas, ellas son:
Las funciones elementales son los bloques de construcción básicos de las matemáticas, ellas son:
- Funciones polinómicas
- Funciones racionales
- Funciones radicales
- Funciones trascendentes y
- Funciones especiales
Funciones Polinómicas
La forma de una función polinómica es la siguiente:
![]()
Donde: ![]() para cada i = 0, 1, 2, 3, 4, . . . , n
para cada i = 0, 1, 2, 3, 4, . . . , n
![]()
Características de las funciones polinómicas
- Su dominio pertenece al conjunto de los números reales
 .
. - El rango de estas funciones siempre pertenece al conjunto de los números reales
 .
. - Son continuas.
Se dice que y = f(x) es una función polinómica de grado n. En este tema se trabajará con los grados n = 0, 1 y 2.
Tipos de funciones polinómicas
Este tipos de funciones elementales se clasifican según el grado del polinomio, el cual determina la forma de su gráfica y su comportamiento. Los tipos más comunes son:
- Función constante.
- Función lineal.
- Función afín.
- Función cuadrática.
Función constante
| Es una una función polinómica de grado cero y se define como: |
Características de la función constante
- Es una recta paralela con respecto a eje “x”
- Su dominio es el conjunto de los números reales.

- Su rengo es únicamente el valor constante.

- No es inyectiva ni sobreyectiva.
Ejemplo:
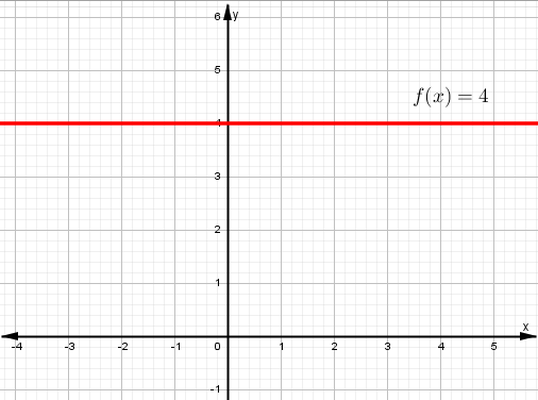
Ejemplo. Determina dominio, rango, punto de corte en el eje “y” y graficar.
$$f(x)=\sqrt{3}$$
Solución
- Gráfica
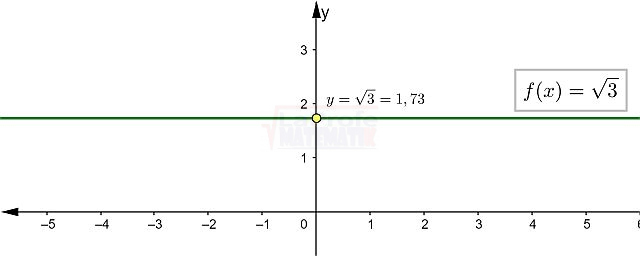
- Dominio:

- Rango:

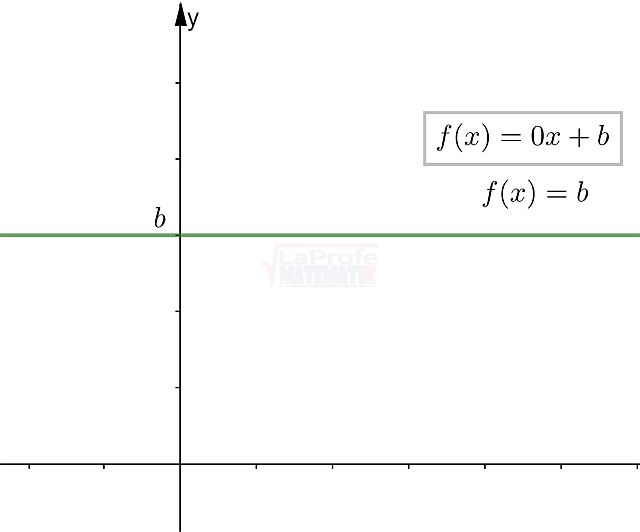
- Como es una función constante la recta pasa por el eje «y» en
 , esto es aproximadamente igual a 1,73.
, esto es aproximadamente igual a 1,73. - Punto de corte en el eje “y” es (0,√3)
Función lineal
| Es una función polinómica de variable real de primer grado. Su forma es y = f(x) = mx. Donde m es una constante llamada pendiente. |
Características de la función lineal
- El dominio y rango pertenecen al conjunto de los números reales.
- Gráficamente es una recta que siempre pasa por el origen del plano cartesiano.
- Es creciente cuando m es positivo y es decreciente cuando m es negativo.
- Para construir gráficamente la recta basta con conocer dos puntos del plano cartesiano que satisfagan la ecuación.
- Es una función biyectiva.
Cálculo de la pendiente m
Para determinar el valor de la pendiente debes aplicar la siguiente fórmula:
![]()
Donde:
![]()
Son las coordenadas de dos puntos ![]()
Función afín
| Es una función polinómica de primer grado, su forma y = f(x) = mx+b. Donde m y b son números reales constantes y b ≠ 0 |
Características de la función afín
- El dominio y rango pertenecen al conjunto de los números reales.
- Gráficamente es una recta que nunca pasa por el origen del plano cartesiano.
- Es creciente cuando m es positivo, decreciente cuando m es negativo y si m = 0 la función es constante.
- Para construir gráficamente la recta basta con conocer dos puntos del plano cartesiano que satisfagan la ecuación.
- b es el punto donde la recta intercepta el eje vertical “y”, es llamado punto de corte en el eje de las ordenadas.
- Función biyectiva.
Ejemplo
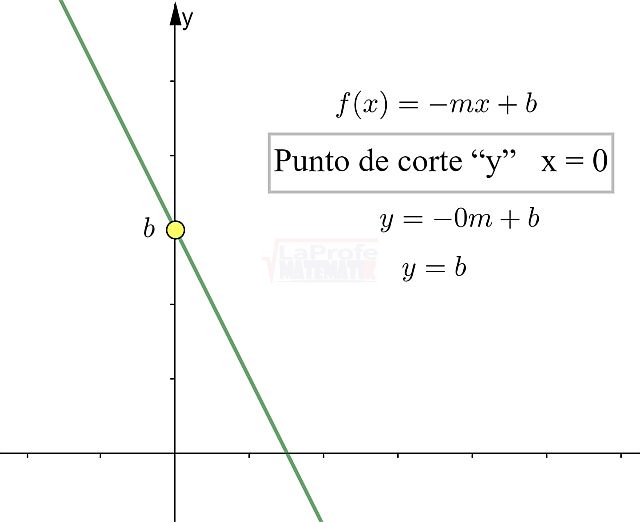
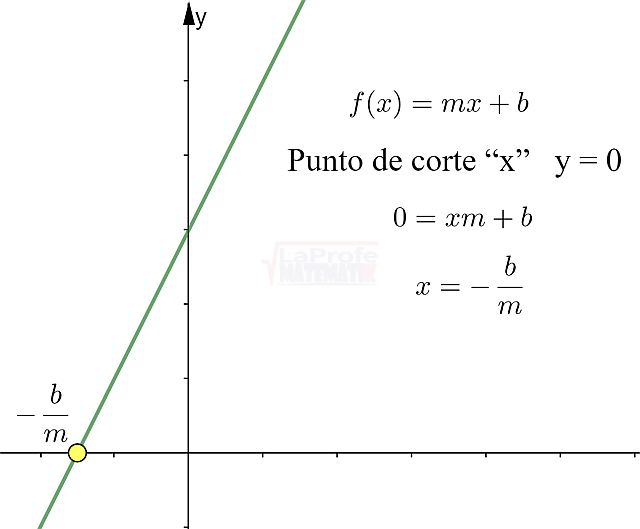
Ejemplo. Graficar y determinar si la función es creciente o decreciente, puntos de corte con respecto al eje x e y, dominio y rango.
![]()
Solución
Se calcula primero los puntos de cortes y luego se traza la recta en el plano cartesiano.
Punto de corte con el eje “x” “y = 0”
![]()
![]()
![]()
Punto de corte con el eje “x” = (-10,0)
Punto de corte con el eje “y” “x = 0”
![]()
![]()
Punto de corte con el eje “y” = (0,5)
Gráfica:
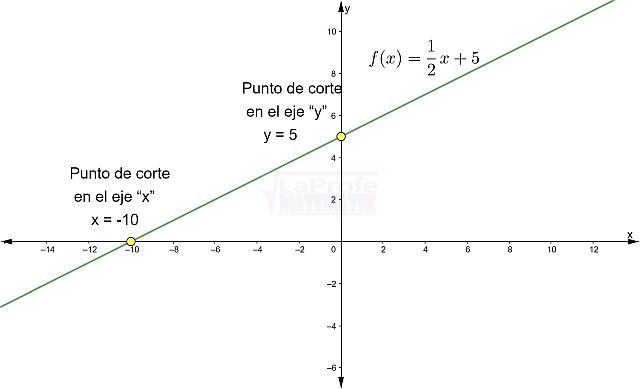
Es creciente ya que m = ½ > 0
Dominio y rango
![]()
![]()
Simulador de la función lineal y afín
Con este simulador explorarás de forma interactiva un tipo de funciones elementales muy interesante llamadas función lineal y función afín. Te ayudará a fortalecer lo aprendido y te volverás un experto construyendo gráficas modificando la pendiente y el punto de corte en el eje y.
Verás cómo cada cambio en la fórmula y = mx + b afecta directamente a la línea recta, ayudándote a visualizar y entender conceptos clave de forma sencilla y divertida.
Función cuadrática
| Es una función polinómica de segundo grado al graficarla recibe el nombre de parábola, definida como: |
Características de la función cuadrática
- Cuando a>0 abre hacia arriba es decir es cóncava hacia arriba.
- Cuando a<0 abre hacia abajo es decir es cóncava hacia abajo.
- El dominio de la función pertenece al conjunto de los números reales.

- El rango de la función se calcula de la siguiente manera:
Sí a>0 el rango de la función es:
![]()
Sí a<0 el rango de la función es:
![]()
- Posee un eje de simetría que pasa por su vértice V(x,y).
- Cuando a > 0 su vértice V(x,y) es un punto mínimo.
- Cuando a < 0 su vértice V(x,y) es un punto máximo.
Cálculo del vértice, coordenada “x”
![]()
Cálculo del vértice, coordenada “y”
![]()
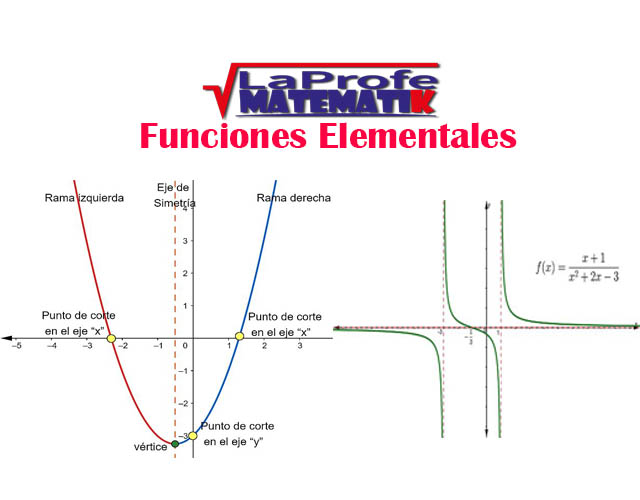
Ejemplo gráfico

Simulador de la función cuadrática
Este simulador fue hecho pensando en ti, para que pongas en practica lo aprendido y fortalezcas tus conocimientos con las funciones elementales. Así que atrévete y juega en el simulador de la función cuadrática.
Ejemplo. Graficar la función y determinar tipo de concavidad, dominio, rango, vértice, puntos de corte (eje x e y) y diga si existe un mínimo o un máximo.

Solución
Paso # 1: Extraer los valores
![]()
Paso # 2: Tipo de concavidad.
Como ![]() , entonces es cóncava hacia arriba y por ende posee un punto mínimo.
, entonces es cóncava hacia arriba y por ende posee un punto mínimo.
Paso # 3: Determinar el rango de la función.
Se aplica:
![]() ,
,
Para determinar la coordenada “x” se necesita los valores de b y a
b = 6 ∧ a = 3

La función es:
![]()
Se sustituye el valor de x = –1
![]()
![]()
![]()
![]()
![]()
El rango de la función es desde -4 hacia el infinito positivo.
![]()
Paso # 4: Determina el valor del vértice
Con los valores anteriores de:
x = –1
y = -4
Las coordenadas del vértice es:
![]()
Paso # 5: Determinar punto de corte con respecto al eje “x”. Se aplica la fórmula de la resolvente
![]()
Sustituir los valores de a, b y c.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Paso # 6: Determinar el punto de corte con respecto al eje “y” donde x = 0
Función:
![]()
Sustitución del valor de x = 0
![]()
![]()
![]()
Paso # 7: Se grafica en el plano cartesiano los puntos vértice y de corte con el eje x e y
- Vértice:

- Punto de corte eje “x”
 ∧
∧ 
- Punto de corte eje “y”

Luego trazar los ramales de la parábola
- Ramal de la izquierda, desde el punto de corte en “x” hasta el vértice
- Ramal de la derecha, desde el vértice hasta los puntos de corte “y” e “x”
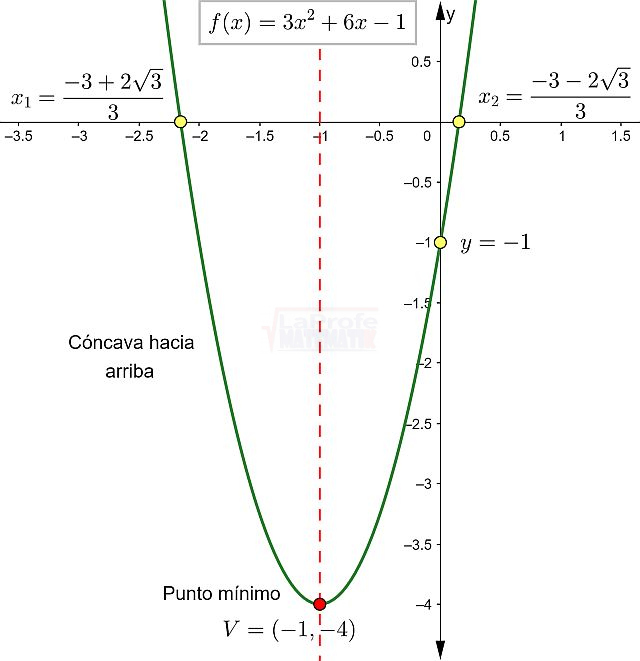
Paso # 8: Dominio de la función
![]()
Función cuadrática: explicación completa (video)
Hasta ahora ¿Te cuesta entender la función cuadrática? ¡No te preocupes! En este video te lo explicamos todo paso a paso: qué es una función cuadrática, sus características principales, cómo encontrar el vértice, los puntos de corte y, lo más importante, ¡cómo graficar una parábola de forma sencilla! Así que prepárate para dominarla este tipo de funciones elementales.
Funciones Racionales
Es otro tipo de funciones elementales, y su forma es ![]() donde
donde ![]() y
y ![]() son polinomios, es decir es el cociente de dos polinomios.
son polinomios, es decir es el cociente de dos polinomios. ![]() ≠ 0
≠ 0
Algunas de estas funciones pueden presentarse así:
![]() El
El ![]()
![]() El
El ![]()
![]() El
El ![]()
Gráfica de una función Racional
Para realizar la gráfica de una función racional es necesario tener los valores para los cuales la función no está definida. Estos valores, que hacen que el denominador sea cero, corresponden a las asíntotas verticales de la gráfica.
Asíntota vertical
Es una recta vertical x = a de una función racional f , si f ( x ) → ∞ o si f(x) → -∞ cuando x se aproxima a “a” por la izquierda o por la derecha.
La expresión polinómica es localizada en el denominador y se iguala a cero para obtener el valor o los valores de x que viene siendo las rectas verticales o asíntotas.
Asíntota horizontal
Es una recta horizontal (m = 0) y = c de una función racional f , si f ( x ) → c cuando x → ∞ o cuando x → – ∞
Dada la función racional f definida por:

Cuando:
 , la función f no tiene asíntota horizontal
, la función f no tiene asíntota horizontal , la función f tiene una asíntota horizontal en el eje “x”
, la función f tiene una asíntota horizontal en el eje “x”
$$y=0$$
 , la función f tiene una asíntota horizontal y es la recta:
, la función f tiene una asíntota horizontal y es la recta:
$$ y=\frac{a_{n}}{b_{m}}$$
Es decir, dividir el coeficiente del numerador entre el coeficiente del denominador.
Asíntota oblicua
Es una recta que posee una pendiente distinta a cero. ¿Cómo identificar si una función racional posee una asíntota oblicua?, te recomiendo que observes la siguiente expresión:
$$f(x)=\frac{R(x)}{S(x)}=\frac{ax^{n+1}}{bx^{n}}$$
- Identificar la existencia. Cuando la diferencia entre el grado del polinomio del numerador y del denominador es 1 la función posee asíntota oblicua.
- Calculo de la ecuación de la asíntota. Para hallar la ecuación debes dividir el polinomio del numerador entre el denominador, el cociente es la ecuación de la asíntota oblicua.
Características de las funciones racionales
- El dominio son todos los valores del conjunto de los
 a excepción de aquellos que anulen el denominador.
a excepción de aquellos que anulen el denominador.
- El rango son todos los valores del conjunto de los
 a excepción cuando existe asíntotas horizontales.
a excepción cuando existe asíntotas horizontales. - Son discontinuas en los valores de “x” que anulan al denominador.
- Poseen asíntotas verticales siendo el valor de “x” que anula al denominador
- Pueden poseer asíntotas horizontales sólo cuando en 2 casos.
😆 Cuando el grado del polinomio del numerador es menor que el grado del polinomio del denominador
😆 Cuando los grados del polinomio tanto del numerador y del denominador sean iguales.
Gráfica de una función racional
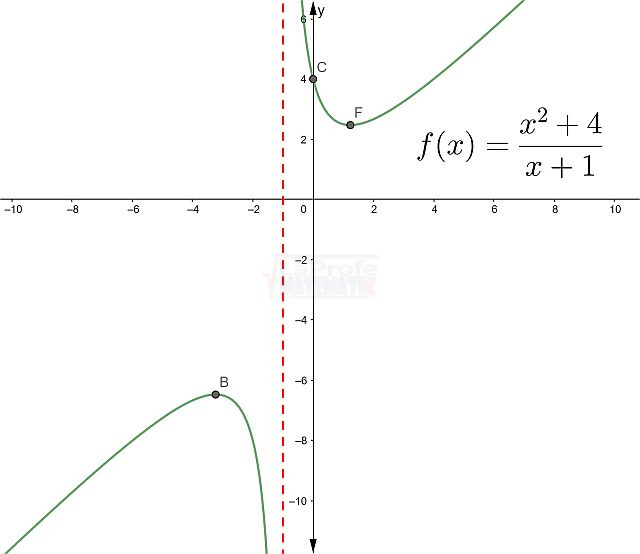
Ejemplo. Analiza y grafica la siguiente función racional.
![]()
Paso # 1: Determinar las raíces del numerador
Como el numerador existe una constante, entonces no se determina las raíces. Por lo tanto no corta en el eje “x”
Paso # 2:Determine las raíces en el denominador para lo cual la función no está definida.
![]()
Paso # 3:Hallar las asíntotas verticales, si existen.
Como está indefinida en: ![]() . La asíntota es:
. La asíntota es:
![]()
Paso # 4: Determinar puntos de cortes en el eje “y”.
No existe punto de corte en “y” ya que el resultado es indefinido.
![]()
Paso # 5: Determinar las asíntotas horizontales, si existe.
En esta función el grado del polinomio del numerador es menor que el grado del polinomio del denominador.
![]() y = 0
y = 0
Existe una asíntota horizontal en el eje “x”
Paso # 6: Crear la tabla de valores y obtener los valores de la variable dependiente “y”
| x | -2 | -1 | 0 | 1 | 2 |
| f(x) | -1 | 1 |
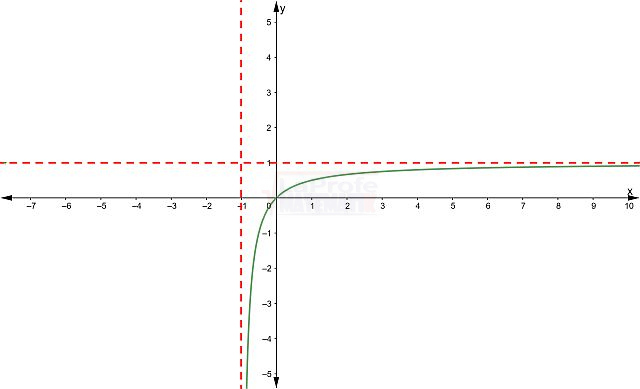
Paso # 7: Gráfica
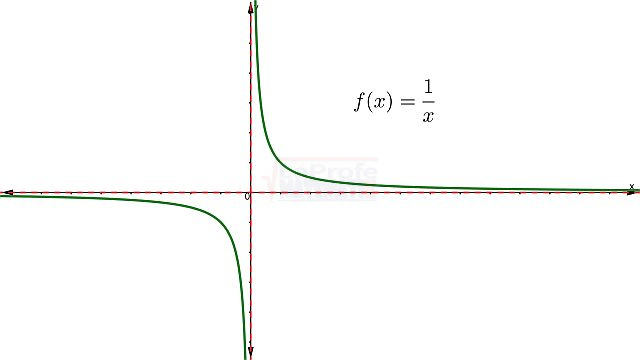
Paso # 8: Dominio y rango
![]()
![]()
Ejemplo. Analiza y grafica la siguiente función racional.
![]()
Paso # 1: Determinar las raíces del numerador, es decir f(x) = 0
![]()
![]()
Esto quiere decir que la función corta en las coordenadas (-1,0)
Paso # 2: Determine las raíces en el denominador para lo cual la función no está definida. En este ejemplo el denominador es una expresión cuadrática, para determinar las raíces se puede aplicar la resolvente o factorizar.
En nuestro caso escogemos la factorización
![]()
![]()
![]()
![]()
![]()
No está definida en: ![]() y
y ![]()
Paso # 3: Hallar las asíntotas verticales, si existen.
Son las rectas ![]() y
y ![]()
Paso # 4: Determinar puntos de cortes en el eje “y”
Se sustituye 0 en la función:
![]()
La función corta en el y = -1/3
Paso # 5: Determinar las asíntotas horizontales, si existe.
En esta función el grado del polinomio del numerador es menor que el grado del polinomio del denominador. Es decir:
Existe una asíntota horizontal en el eje “x”
![]()
y = 0
Paso # 5: Crear la tabla de valores
| x | -2 | -1 | 0 | 1 | 2 |
| f(x) | 0 |
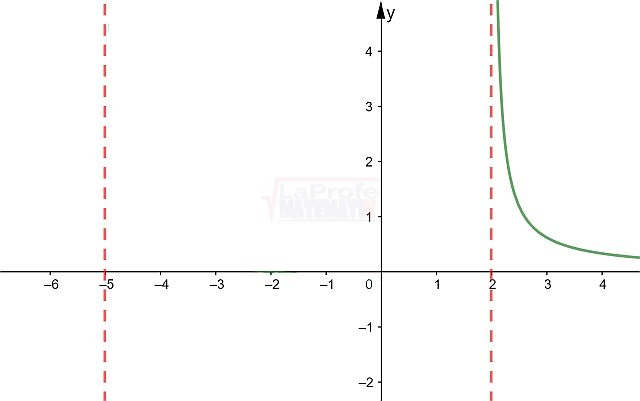
Paso # 6: Gráfica
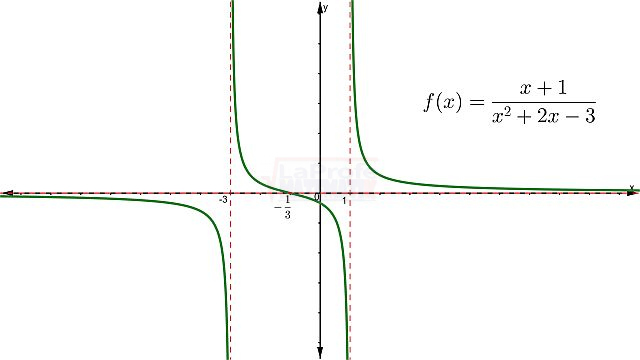
Paso # 8: Dominio y rango
![]()
![]()
Funciones Radicales
| Es otro tipo de funciones elementales denominadas también funciones irracionales (porque la variable independiente x está dentro del signo radical), son de la forma |
Características de las funciones radicales
- El dominio depende del índice de la raíz. “Si el índice es par, posee restricción # 1 del dominio ”. Cuando existen raíces pares de un número negativo. “Si es índice es impar, la función esta definida para todos los números
 .”
.” - Rango. Para conocer exactamente desde donde comienza el rango, se sustituye en la función el primer valor del dominio.
- Cálculo de puntos de cortes. Para determinar el intercepto en el eje “y” x = 0 y para determinar el intercepto en el eje “x” y = 0
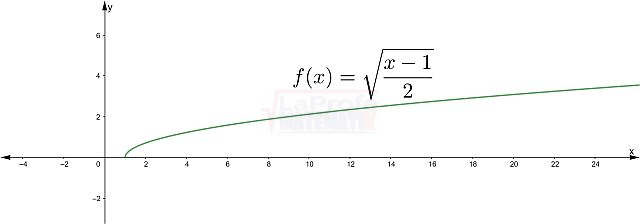
Ejemplo. Analiza y grafica.
Paso # 1: Identificar el índice de la raíz
El índice del radical es 2, por lo tanto es par.
Paso # 2: Determinar el primer valor del intervalo del dominio
![]()
![]()
![]()
Paso # 3: Intervalo del dominio
![]()
Paso # 4: Determinar el primer valor del intervalo del rango, sustituyendo el primer valor del intervalo del dominio en la función dada

![]()
![]()
Paso # 5: El intervalo del rango es:
![]()
Paso # 6: Cálculo de punto de corte en “x” y = 0
![]()
![]()
![]()
![]()
![]()
![]()
Paso # 7: Cálculo de punto de corte en “y” x = 0
![]()
No corta en y
Paso # 8: Gráfica

Función radical con índice par (video)
Te invito que veas este video, te ayudará a consolidar y profundizar los conocimientos adquiridos
Funciones Trascendentes
| Son otros tipos de funciones elementales, donde la variable “x” funciona como exponente, como argumento de las funciones trigonométricas y logarítmicas. Algunas de las funciones trascendentes se clasifican como: exponenciales, logarítmicas, trigonométricas y sus inversas. |
Función Exponencial
| La función exponencial es de la forma f(x) = ax , donde la base a es una constante con signo positivo y diferente del número 1, y el exponente “x” es la variable. |
Este tipo de función es usada para mostrar el crecimiento de poblaciones, interés de dinero acumulado, desintegración radioactiva, entre otros.
Características de las funciones exponenciales
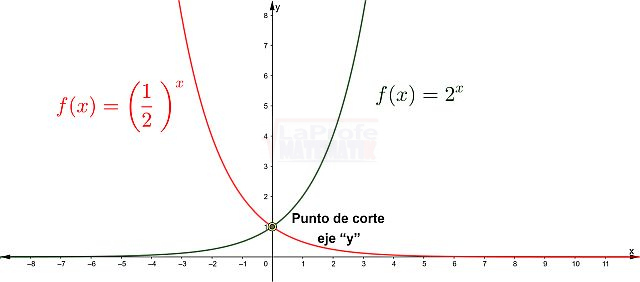
- Si el valor de la base a > 1 , entonces f es una función creciente. Como muestra la función g(x)=2x
- Si el valor de la base a (está entre 0 y 1) es decir 0 < a < 1 , f es una función decreciente. Como muestra la función f (x)=(1/2)x
- Punto de corte en el eje “x” No existe.
- Punto de corte en el eje “y” es:
y = 1 - La función siempre pasa por el punto (1,a), debido que:

- El dominio de una función exponencial es el conjunto de los números reales
 . Dom f =
. Dom f = 
- El rango es el conjunto de los números reales positivos
 . Rgo f=
. Rgo f= = (0,+∞)
= (0,+∞) - Es inyectiva pero no es sobreyectiva.
Ejemplo. Realiza el estudio de la función y graficar.
![]()
Paso # 1: Observar si la base “a” es mayor que 1 o está comprendida entre 0 y 1.
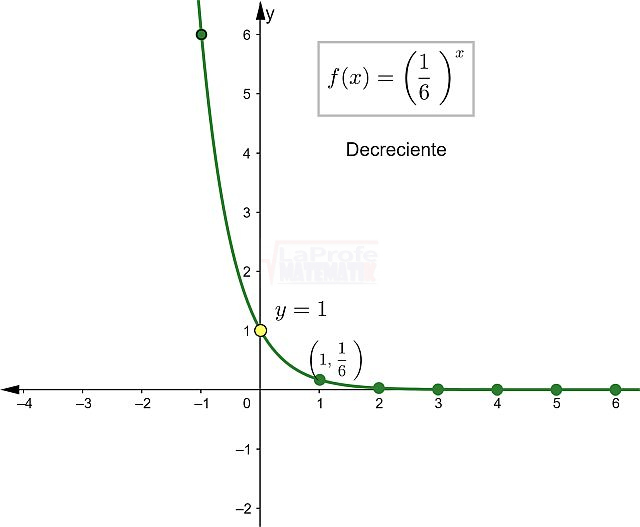
Como 0 < a < 1 , la función es Decreciente
Paso # 2: Punto de corte en “x”. No existe
Paso # 3: Determinar punto de corte en “y” x = 0
![]()
![]()
![]()
Paso # 4: Determinar el dominio
Dom f = ![]()
Paso # 5: Determinar el rango
Rgo f=![]()
Paso # 6: La función siempre pasa por el punto (1,a). En este caso el punto es:
![]()
Paso # 7: Crear la tabla de valores
| x | -2 | -1 | 0 | 1 | 2 |
| f(x) | 36 | 6 | 1 |
Paso # 8: Gráfica
Función Logarítmica
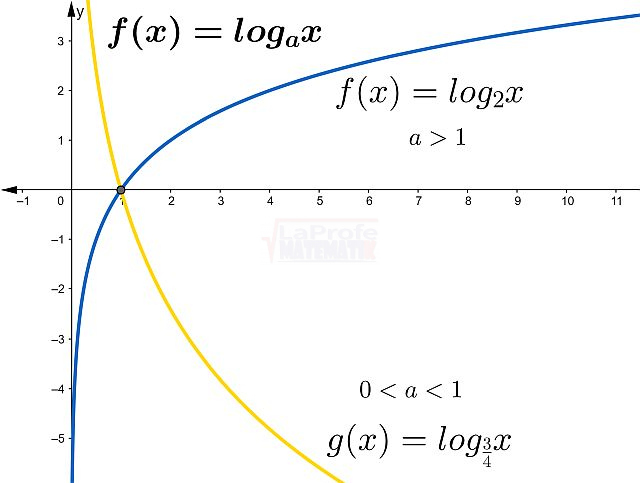
| Las funciones logarítmicas son las inversas de las funciones exponenciales, y su forma es: a > 0 a ≠ 1 Definida para todo x>0 Se verifica como: |
Características de las funciones logarítmicas
- El dominio es:

- El rango es:

- Punto de corte en el eje “y”. No existe
- Es Creciente cuando

- Es Decreciente cuando:

- La función siempre pasa por el punto (a,1) , pues al realizar

- Es Biyectiva
Ejemplo. Analiza y grafica la siguiente función.
![]()
Paso # 1: El dominio de la función siempre es:![]()
Paso # 2: El rango de la función siempre es:![]()
Paso # 3: Punto de corte en el eje “x” y = 0
![]()
![]()
![]()
Paso # 4: Punto de corte en el eje “y” x = 0
![]()
![]()
No existe punto de corte en el eje “y”
Paso # 5: Creciente o decreciente.
Como ![]() entonces
entonces ![]()
Es decreciente.
Paso # 6: La función siempre pasa por el punto (a,1), pues al realizar
![]()
![]()
Funciones Especiales
Las funciones especiales son una categoría que agrupa a funciones que, aunque no encajan en las clasificaciones más comunes (como las polinómicas o exponenciales), son de gran importancia en el cálculo y otras áreas de las matemáticas. Un ejemplo notable es la función de valor absoluto, que se define como la distancia de un número al origen, sin importar su signo. Su gráfica forma una figura en «V», lo que la distingue claramente de otros tipos de funciones.
Dentro de las funciones especiales están:
- Funciones segmentadas o funciones a trozos
- Función parte entera o mayor entero y
- Función valor absoluto
En este post sólo se desarrollará la función de valor absoluto.
Función de valor absoluto
La función de valor absoluto asigna a cada elemento del dominio su valor absoluto y es de la forma:
![]()
Características de las funciones de valor absoluto
- El dominio es:

- El rango es:

- Punto de corte en el eje “x” cuando f (x) = y = 0
Se iguala la expresión a 0 - Punto de corte en el eje “y” cuando x = 0
- El vértice de la curva es el valor de x
- El eje de simetría es la recta que pasa por el vértice, paralela al eje “y”
- Es Decreciente en el intervalo: (-∞,x]
- Es Creciente en el intervalo: [x,∞)
- No es inyectiva, ni sobreyectiva
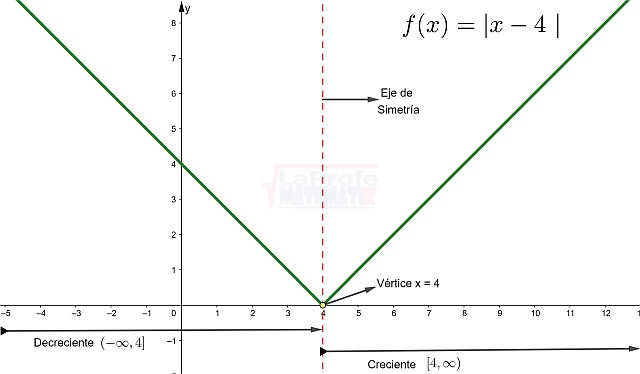
Ejemplo. Graficar la función a continuación:

Paso # 1: Dominio de la función ![]()
Paso # 2: Rango de la función![]()
Paso # 3:Punto de corte en el eje “x” y = 0
![]()
![]()
![]()
![]()
Paso # 4: Punto de corte en el eje “y” x = 0
![]()
![]()
![]()
![]()
Paso # 5: Se traza el eje de simetría que pasa por el vértice.
Paso #6: Es Decreciente en el intervalo.
(-∞,4]
Paso # 7: Es Creciente en el intervalo.
[4,∞)

Actividades
- Determinar las características de todas las funciones elementales y finalmente grafique.











- Dibujar la parte que falta en la gráfica de cada función




- Analizar cada función racional. Luego, crear la gráfica












- Analiza cada función radical. Luego, realizar su gráfica






- Analiza cada función exponencial, Luego, realice la gráfica.






- Trazar la gráfica de cada función y analizar su comportamiento






- Trace la gráfica de cada función y analice su comportamiento



- ¿Cuál de las siguientes funciones es decreciente en todo su dominio?




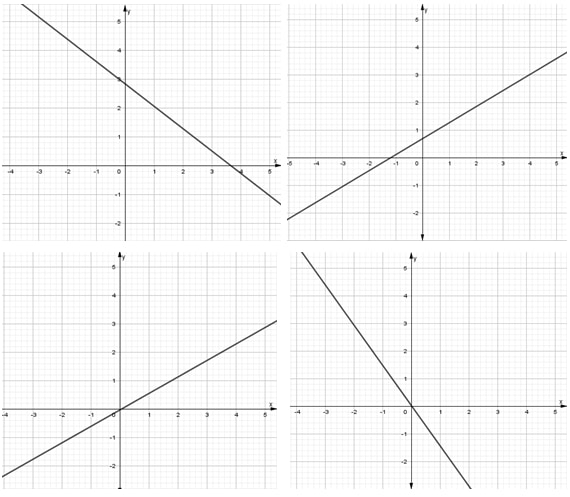
- Identifica si cada función es lineal o afín a partir de su gráfica.

- Interpreta cada expresión y diga si es una función afín, lineal o ninguna de las dos.
$$y=\frac{1}{2}x-3$$
$$y=2x^{2}$$
$$y=5x+7$$
$$y=-8x$$
$$y=\frac{5}{9}x$$
- Lee y selecciona la afirmación que es falsa. De la función $$-5x-8=y$$ Se puede afirmar que:
A. Es una función afín.
B. Es creciente.
C. El intercepto con el eje y es (0,-8)
D. El intercepto con el eje x es (-8/5,0) - Calcule los interceptos con los ejes, la pendiente y dibuje su gráfica de las siguientes funciones:
a.) y-2x=3
b.) 3x+4y=12
c.)3y=-6x+3
d.) 2y+3x=-1