¿Sabías que entender las características de las funciones te permite resolver problemas matemáticos de manera mucho más rápida? Al conocer sus propiedades, puedes interpretar su comportamiento y predecir su curva con solo ver su expresión algebraica, sin necesidad de graficar. Esto te da una comprensión profunda de lo que la función representa, agilizando tu estudio analítico y dándote una ventaja para interpretar cualquier expresión matemática.
Características de las funciones
Conocer las características de las funciones te permite interpretar sus expresiones algebraicas de forma directa, sin necesidad de graficar, lo que facilita la resolución de problemas y la toma de decisiones en diversas disciplinas. A continuación, te menciono algunas de ellas:
- Puntos de cortes o intersecciones.
- Funciones creciente y decrecientes.
- Funciones pares e impares (simetría).
- Funciones periódicas.
Puntos de corte
Los puntos de corte indica donde la recta o la curva intercepta con los ejes del plano cartesiano. Estos puntos están formados por una variable independiente “x” y la dependiente “y” . Para calcular el punto debes aplicar las siguientes relaciones:
- Corte o intersección con el eje “x” → y = 0
- Corte con el eje “y” → x =0
Ejemplo. Determine los puntos de cortes con respecto a los ejes “x” e “y”
$$f(x)=\frac{6x+12}{3}$$
Paso # 1: Se iguala f ( x ) = y
$$y=\frac{6x+12}{3}$$
Paso # 2: Sustituir x = 0 , para obtener la intersección en con el eje “y”
$$y=\frac{6x+12}{3}$$
$$y=\frac{6\cdot 0+12}{3}=\frac{12}{3}$$
$$y=4$$
Punto de corte: A(0,4)
Paso # 3: Sustituir y = 0 , para obtener la intersección con el eje “x”
$$0=\frac{6x+12}{3}$$
$$0=6x+12$$
$$6x=-12$$
$$x=-2$$
Punto de corte: B(-2,0)
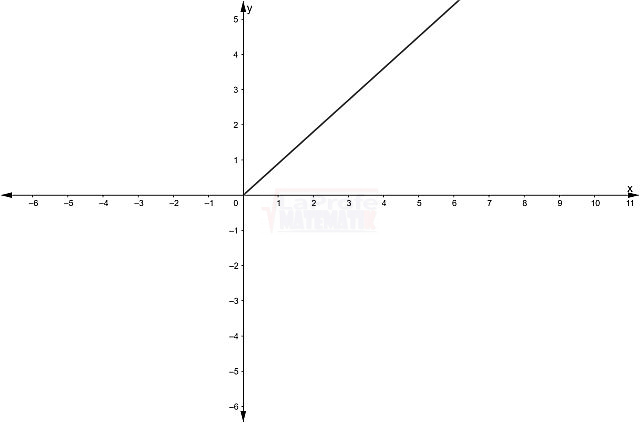
| Como es una función lineal, solo necesitas encontrar sus dos puntos de corte (con los ejes x e y) para graficarla. Una vez que tengas ambos puntos, traza una línea recta que pase por ellos para completar la gráfica. |
Observa la gráfica
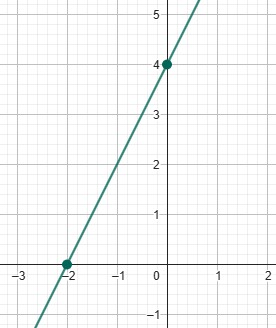
Funciones crecientes y decrecientes
Al analizar un gráfico que muestra los cambios de temperatura a lo largo de un año, la clave está en el estudio de sus intervalos. Interpretar las variaciones de la curva te permite identificar rápidamente los momentos de temperaturas máximas y mínimas. Este análisis, que te enseña a reconocer intervalos crecientes, decrecientes o constantes, es fundamental para entender el comportamiento de los datos y tomar decisiones informadas.
Funciones crecientes
| La función es creciente en el intervalo [a,b] si al aumentar los valores de x aumenta los valores de f ( x ). Es decir, si x1 < x2 , entonces, f ( x1 ) < f ( x2 ). Para todo x1, x2 en[a,b]. |
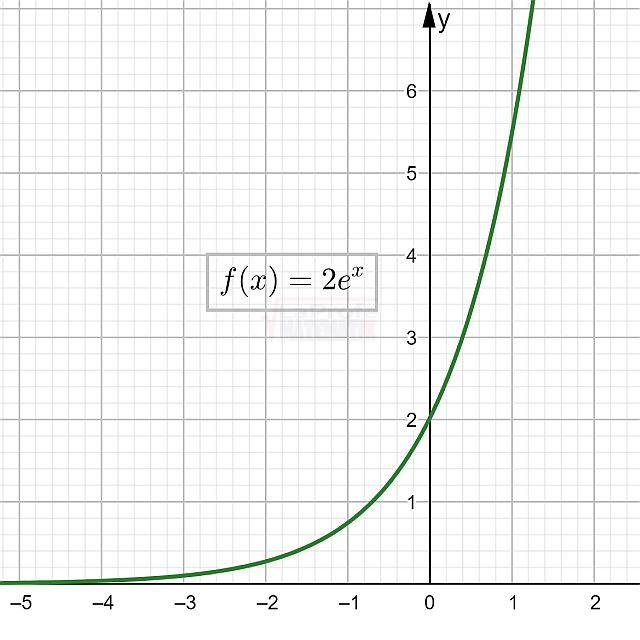
Por ejemplo: la función$$f(x)=2e^{x}$$Es creciente.
Observa que: x 1 < x 2 implica que f ( x 1 ) < f ( x 2 )
Se toman valores arbitrarios de x1= -1 y x2 = 0 ⇒ f (0,7) < f (2)
Se cumple que la función$$f(x)=2e^{x}$$Es creciente en todo el conjunto de los números reales.
Funciones decrecientes
| La función es decreciente en un intervalo [a,b] si al aumentar los valores de x disminuyen los valores de f ( x ). Es decir, si x1 < x2 , entonces, f ( x1 )>f ( x2 ) para todo x1, x2 en [a,b]. |
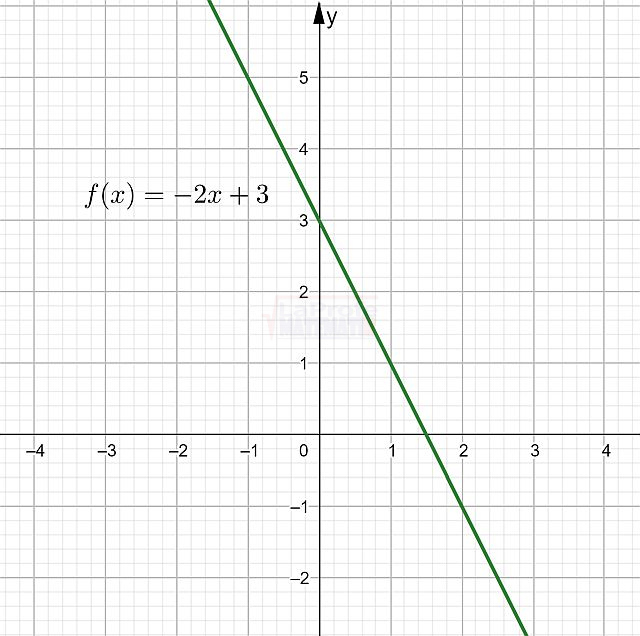
Ejemplo: la función$$f(x)=-2x+3$$Es decreciente
Observa al aplicar: x 1 < x 2 implica que f ( x 1 ) > f ( x 2 ).
Se toman valores arbitrarios de x1= -2 y x2 = 0 ⇒ f (7) > f (3)
Se cumple que la función$$f(x)=-2x+3$$Es decreciente en todo su dominio.
Observa la gráfica:
Función constante
| Una función es constante en el intervalo [a,b] cuando no es creciente ni decreciente. Es decir, f ( x 1 ) = f ( x 2 ) para todo x1, x2 en [a,b]. |
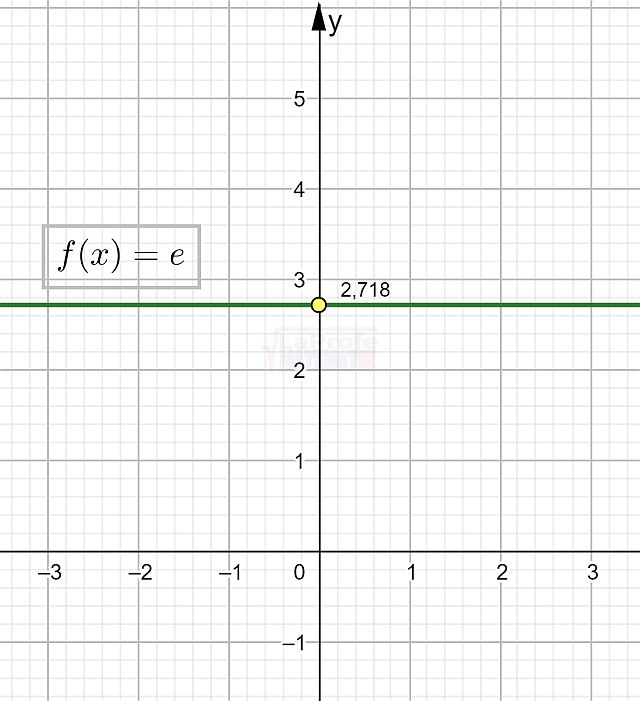
Por ejemplo: la función$$f(x)=e$$Es constante.
Observa al aplicar: x 1 < x 2 implica que f ( x 1 ) = f ( x 2 )
Se toman valores arbitrarios de x1= 1 y x2 = 0 ⇒ f (e) = f (e)
Se cumple que la función$$f(x)=e$$es constante en el intervalo (-∞, ∞).
Observa la gráfica:
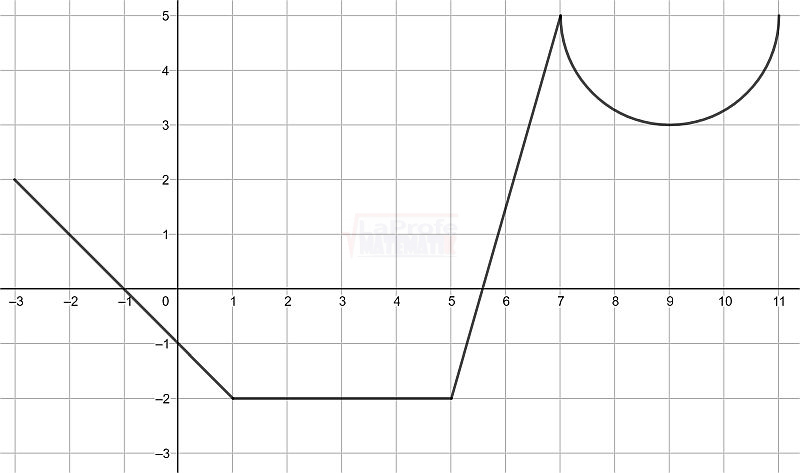
Ejemplo. Determine los intervalos en los cuales el modelo gráfico de la función f es creciente, decreciente o constante.
Analiza la siguiente gráfica e identifica los intervalos donde la función es creciente, decreciente o constante.
.
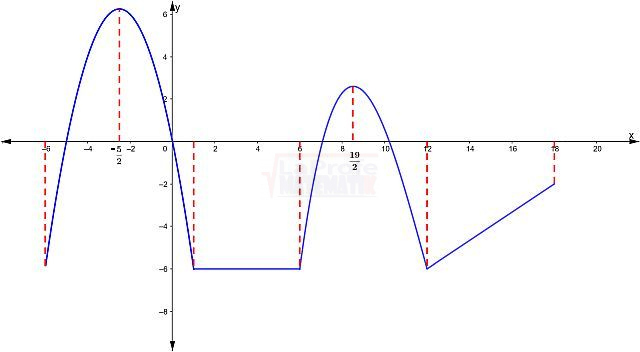
Es creciente en los intervalos:
$$\left [ -6,-\frac{5}{2} \right ]$$
$$\left [ 6,\frac{19}{2} \right ]$$
$$\left [ 12,18 \right ]$$
Es decreciente en los intervalos:
$$\left [ -\frac{5}{2},1 \right ]$$
$$\left [ \frac{19}{2},12 \right ]$$
Es constante en el intervalo:
$$\left [ 1,6 \right ]$$
Funciones pares e impares (simetría)
Estas son funciones que se definen por su simetría. Si la función tiene como eje de simetría al eje «y», se le llama función par, este tipo de simetría se les conoce como simetría axial. Si su simetría está ubicada en el origen del plano cartesiano, se le conoce como función impar.
Función Par
Analíticamente la función es par cuando se sustituye la variable “-x” en la función y dé como resultado “f(x)”, es decir no existe ninguna modificación, lo que quiere decir que la curva de la función posee como eje de simetría al eje vertical “y” y por lo tanto se cumple que:
$$f(-x)=f(x)$$
Función Impar
Analíticamente la función es impar cuando se sustituye la variable “-x” en la función y dé como resultado “f (-x)”, es decir que el signo de la función cambia, gráficamente quiere decir que la curva de la función es simétrica con respecto al origen y por lo tanto se cumple que:
$$f(-x)=-f(x)$$
Ejemplo # 1. Determine si la función a continuación es par o impar.
$$f(x)=x^{2}+3$$
Paso # 1:
- Sustituir “-x” en la función
- Comparar el resultado con la función original
- Determinar el tipo de simetría
$$f(x)=x^{2}+3$$
$$f(-x)=(-x)^{2}+3$$
$$f(-x)=x^{2}+3$$
No existe cambio:$$f(-x)=f(x)$$
Analíticamente es: Función par
Gráficamente: Es una función par porque su eje de simetría es el eje “y”. Observa la gráfica:
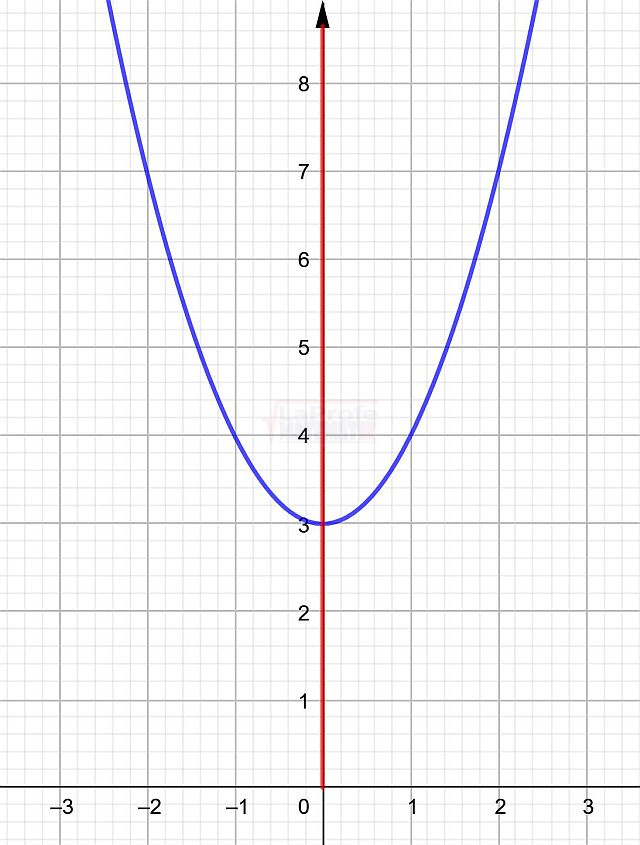
Ejemplo # 2.
Determine si la función es par o impar.
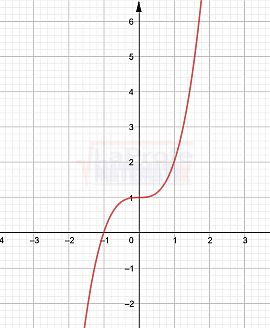
$$f(x)=x^{3}+1$$
$$f(-x)=(-x)^{3}+1$$
$$f(-x)=-x^{3}+1$$
$$f(-x)=-(x^{3}-1)$$
Existe cambio: 
Analíticamente: No es función par ni impar
Gráficamente: No existe eje de simetría en el eje “y” ni con respecto al origen del plano cartesiano. Observa la gráfica.
Ejemplo # 3.
Determine si la función a continuación es pares o impar.
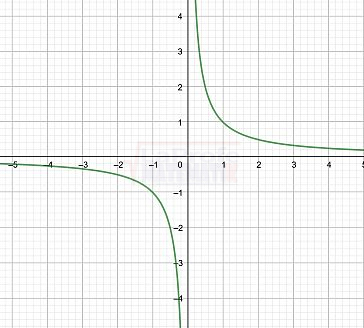
$$f(x)=\frac{1}{x}$$
$$f(-x)=\frac{1}{-x}$$
$$f(-x)=-\frac{1}{x}$$
Existe cambio:$$f(-x)=-f(x)$$
Analíticamente: Es una función impar
Gráficamente: Posee simetría con respecto al origen del plano cartesiano.
Ejemplo # 4:
Determine si la función a continuación es pares o impar.
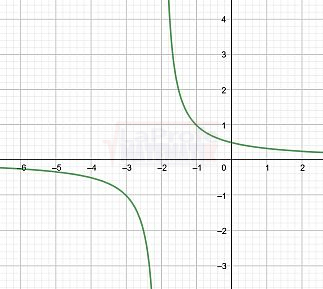
$$f(x)=\frac{1}{x+2}$$
$$f(-x)=\frac{1}{-x+2}$$
$$f(-x)=-\frac{1}{x-2}$$
Existe cambio: Como la
Analíticamente: No es función par ni impar
Gráficamente: No posee simetría.
Características de las funciones periódicas
Cuando se repiten intervalos de iguales longitudes en el dominio estamos en presencia de una función periódica
Entonces una función f : X → Y es periódica cuando existe un número real “T” llamado periodo. Se cumple que cada valor de x que pertenece al dominio de la función es f (x) = f (x + T).
Las funciones trigonométricas en su mayoría son periódicas, mientras que las polinómicas, exponenciales y logarítmicas no lo son.
El periodo (T) de las siguientes funciones trigonométricas es 2π.
- seno,
- coseno,
- secante y
- cosecante.
Las funciones trigonométricas como la tangente y cotangente su periodo (T) es de 
.
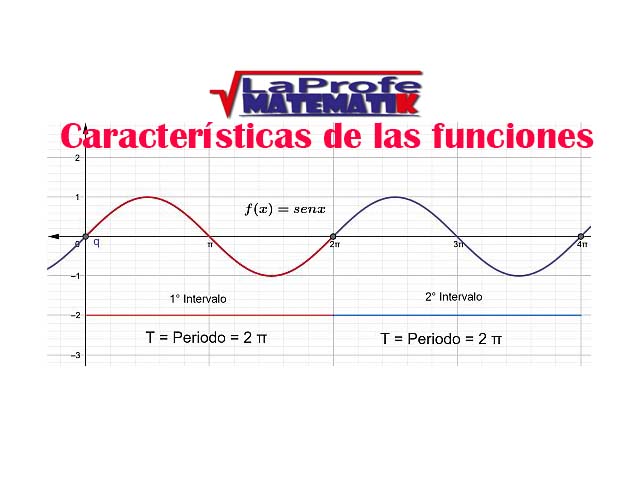
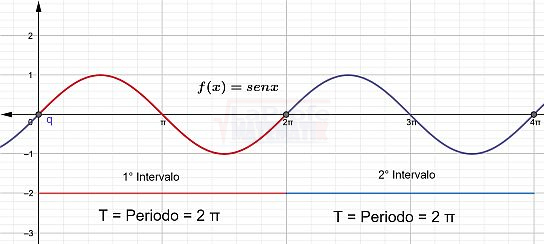
La función$$f(x)=senx$$es un ejemplo perfecto de una función periódica. Su periodo es de 2π, lo que significa que la forma de onda se repite en intervalos de igual longitud, es decir, 2π. Observa la gráfica:
Practica con las funciones trigonométricas
Te presento un simulador bien interesante para que te familiarices con las características de las funciones periódicas.
Actividades
Determine los puntos de cortes en ambos ejes de coordenadas (x e y)
| a. |  | b. |  | c. |  |
| d. |  | e. |  | f. |  |
| g. |  | h. |  | i. |  |
Determine si las siguientes funciones son pares o impares
| a. |  | b. |  | c. |  |
| d. |  | e. |  | f. |  |
| g. |  | h. |  | i. |  |
Dibujar sobre el plano cartesiano el siguiente planteamiento y responde si existen intervalos donde son crecientes, decrecientes o constante explique.
(∞,0] es la función f (x) = x3
(0,5) es la función f (x) = -2x
[5,∞) es la función f (x) = 4x-10
El movimiento de un péndulo en función al tiempo se representa en la siguiente gráfica: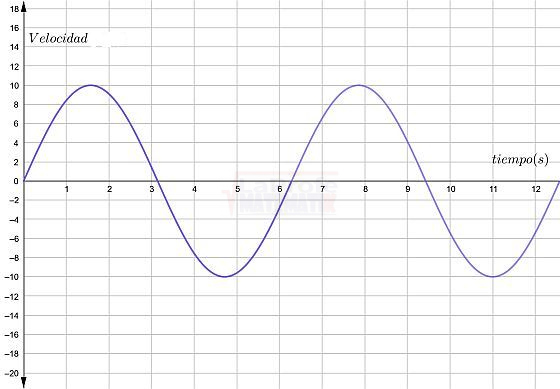
a. ¿Se puede determinar la velocidad del péndulo a los 21 segundos?
b. ¿Cuál es la velocidad del péndulo a los t = 13,5s ?
Complete las curvas en cada gráfica, para que se cumpla cada condición
Par
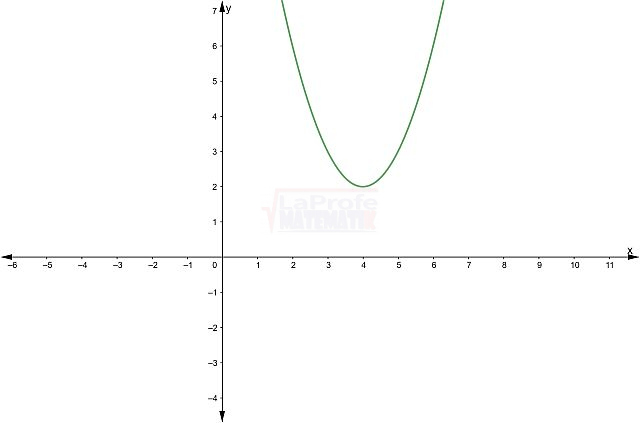
Impar
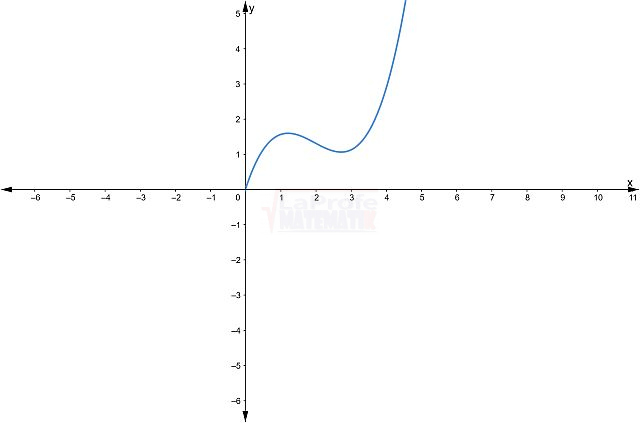
Función par
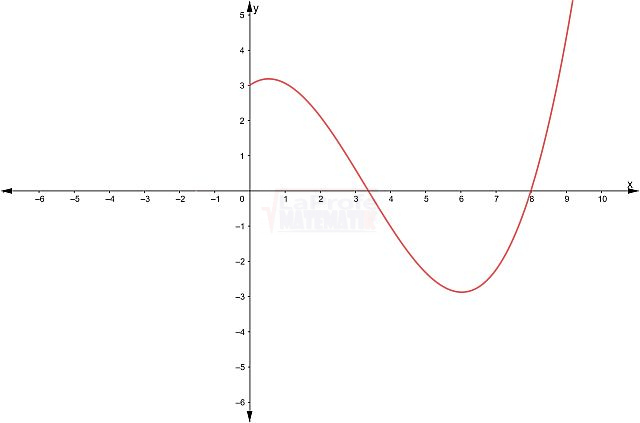
Impar
Determinar los intervalos crecientes, decrecientes y constante
Descubre más desde LaProfematematiK "Dios es Bueno"
Suscríbete y recibe las últimas entradas en tu correo electrónico.