 ¿Alguna vez has intentado convertir un decimal a fracción y terminas con ganas de fraccionar tu cuaderno en mil pedacitos? 😂
¿Alguna vez has intentado convertir un decimal a fracción y terminas con ganas de fraccionar tu cuaderno en mil pedacitos? 😂
Tranquilo, no eres el único. A todos nos ha pasado. Los decimales parecen inofensivos… hasta que alguien dice: “¡Conviértelo en fracción!” y empieza el drama matemático.
Pero aquí viene la buena noticia: detrás de cada decimal —sí, incluso ese 0.75 del precio de las empanadas— hay una fracción escondida, esperando que la descubras como si fuera un secreto de matemáticas nivel ninja. 🥷
En este post te voy a mostrar cómo pasar de decimal a fracción paso a paso, sin fórmulas imposibles ni ataques de pánico.
Prometido: al final vas a mirar esos números con coma y decirles con orgullo, “¡Ya sé quiénes son en realidad!”
Conceptos clave: decimal, fracción y fracción generatriz
Antes de aprender a convertir un número decimal en fracción paso a paso, conviene tener claras algunas ideas básicas. En esta parte descubrirás qué es un número decimal, qué representa una fracción y cómo aparece la famosa fracción generatriz, esa que muestra la forma “real” que hay detrás de cualquier número decimal.
Comprender estos tres conceptos hará que el tema deje de parecer un rompecabezas y se convierta en una historia matemática fácil de seguir y llena de sentido.
Decimal
| Un número decimal es una forma de escribir cantidades que no son enteras, es decir, que tienen una parte “con coma” que representa una fracción del número. Por ejemplo, en 3,75, el 3 es la parte entera y el 0,75 es la parte decimal. |
Fracción
| Una fracción es una forma de representar una parte de un todo que ha sido dividido en partes iguales.$$\frac{a}{b}$$ Donde: a es el numerador (las partes que se toman) b se llama denominador (las partes que divide el todo) Por ejemplo, si te comiste un 1/2 de una pizza, significa que consumiste 1 pedazo de un total de 2 partes iguales. |
Fracción generatriz
| Es la fracción original (irreducible) que al dividir sus elementos (numerador entre el denominador) genera una expresión decimal. Por ejemplo:$$0,35=\frac{35}{100}=\frac{7}{20}$$ |
Entonces, la fracción y el número decimal son distintas formas de expresar lo mismo. Observa la siguiente imagen:
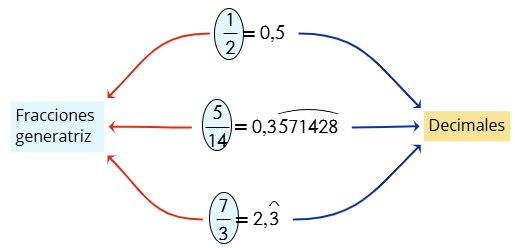
En la información mostrada, las fracciones generatriz son: ½ , 5/14 y 7/3.
Mientras que los decimales generados por cada una de ellas son respectivamente:
- Decimal exacto,
- Periódico mixto y
- Periódico puro.
Conversión de un decimal exacto a fracción
Para determinar la fracción generatriz de un número decimal exacto, debes expresar los decimales a una fracción decimal.
Antes de mencionar el procedimiento para la conversión te muestro las características de un decimal exacto.
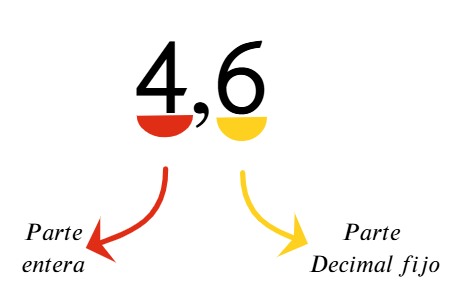
A continuación, el procedimiento para la conversión en tan solo 3 pasos:
- Escribe la parte entera y decimal sin la coma en el numerador.
- En el denominador escribe la potencia de diez con tantos ceros como cifras decimales exprese.
- Simplifica la fracción hasta que quede irreducible.(Recomendable aplicar el Máximo común Divisor M.C.D.)
Ejemplo # 1.
Determina la fracción generatriz de 2,16
| 1° | 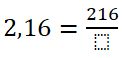 |

El número posee dos decimales, entonces, el denominador es 100.
| 2° | 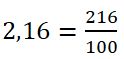 |
| 3° | M.C.D.(216,100) = 4 Se simplifica la fracción entre 4. $$2,16=\frac{216}{100}=\frac{54}{25}$$ |
Respuesta:
$$\frac{54}{25}$$
Ejemplo # 2.
Convertir 0,00004 a fracción.
| 1° | 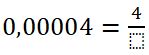 |
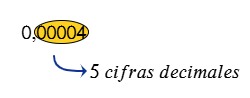
El decimal expresa 5 cifras decimales, entonces, el denominador es de 5 ceros (100 000).
| 2° | $$0,00004=\frac{4}{100\:000}$$ |
| 3° | Se aplica M.C.D. para simplificar la fracción. M.C.D.(4,100 000) = 4. $$0,00004=\frac{4}{100\:000}=\frac{1}{25\:000}$$ |
Respuesta:
$$\frac{1}{25\,000}$$
Conversión de un decimal periódico puro a fracción
Un decimal periódico puro posee las siguientes características:
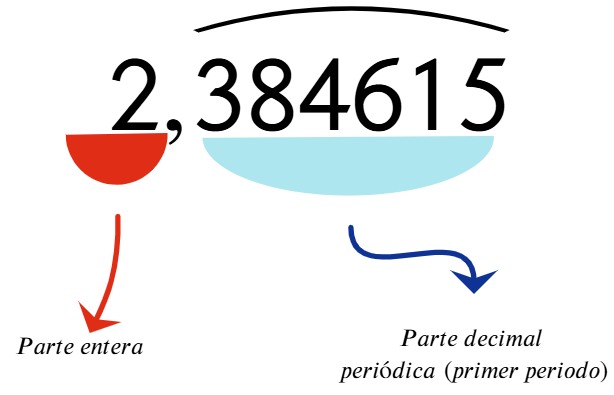
Para hallar la fracción generatriz de un número decimal periódico puro, debes aplicar los siguientes pasos:
- Escribir en el numerador todo el número hasta el final del primer periodo expresado como entero (es decir, sin la coma).
- Restarle su parte entera.
- Escribir en el denominador tantos nueves (9) como la cantidad de cifras que posea el periodo.
- Simplificar.
Ejemplo # 1.
Hallar la fracción de 0,66666…
| 1° | 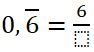 |
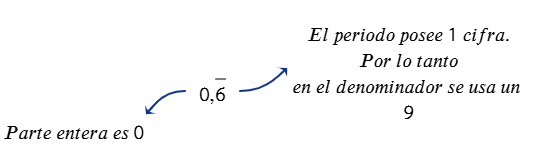
| 2° y 3° | $$0,\overline{6}=\frac{6-0}{9}=\frac{6}{9}$$ |
| 4° | Simplificada queda $$\frac{2}{3}$$ |
Ejemplo # 2.
Determinar la fracción generatriz de 1,18181818…
| 1° | 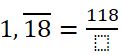 |
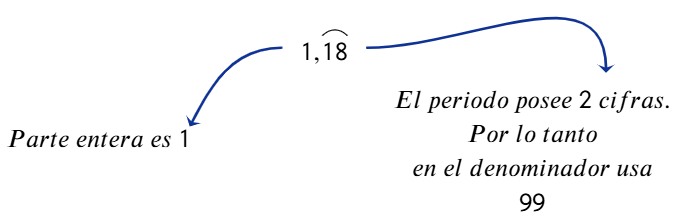
| 2° y 3° | $$1,\overline{18}=\frac{118-1}{99}=\frac{117}{99}$$ |
| 4° | Se aplica M.C.D. para que la fracción sea irreducible. M.C.D.(117, 99) = 9 $$\frac{13}{11}$$ |
Respuesta:
$$\frac{13}{11}$$
Conversión de un decimal periódico mixto a una expresión racional
Para conseguir la fracción generatriz de un decimal periódico mixto, primero debes recordar que:

Ahora sí, el procedimiento para la transformación es el siguiente:
- Escribir en el numerador toda la cifra (en forma entera) hasta el final del primer periodo.
- Agrupar en una cifra el entero y el decimal no periódico, luego restar.
- Escribir en el denominador tantos nueves (9) como cifras tiene el periodo, seguido de tantos ceros como dígitos tiene la parte decimal no periódica.
- Simplificar.
Ejemplo # 1.
Hallar la fracción generatriz del decimal 0,318181818…
| 1° | 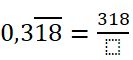 |
| 2° y 3° | $$0,3\overline{18}=\frac{318-3}{990}=\frac{315}{990}$$ |
| 4° | M.C.D. (315,990) = 45 Simplificación $$0,3\overline{18}=\frac{315}{990}=\frac{7}{22}$$ |
Resultado:
$$\frac{7}{22}$$
Ejemplo # 2: Hallar la fracción de 45,6754545454…
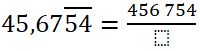 |
| $$45,67\overline{54}=\frac{456\:754-4\:567}{9\:900}=\frac{452\:187}{9\:900}$$ |
| Se aplica el M.C.D. (452 187, 9 900) = 9 Simplificación $$45,67\overline{54}=\frac{452\:187}{9\:900}=\frac{50\:243}{1\:100}$$ |
Resultado:
$$\frac{50\,243}{1\,100}$$
Ejemplo # 3.
Determina la expresión racional de 1,13333…
| 1° | 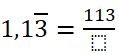 |
| 2° y 3° | $$1,1\overline{3}=\frac{113-11}{90}=\frac{102}{90}$$ |
| 4° | Se aplica el M.C.D. (102, 90) = 6 Simplificación $$1,1\overline{3}=\frac{102}{90}=\frac{17}{15}$$ |
Respuesta:
$$\frac{17}{15}$$
De Decimal a Fracción: Juega y Aprende con Nuestra Simulación Interactiva
¡Es momento de poner a prueba tus conocimientos! Con nuestra simulación interactiva, en ella podrás experimentar con distintos números decimales, generar su fracción equivalente al instante y aprender a identificar si son decimales exactos, periódicos puros, mixtos o incluso irracionales. Es una forma visual, dinámica y divertida de dominar este tema.
¿Estás listo para comenzar la exploración?
¡Queremos Saber Tu Opinión!
Espero que hayas disfrutado la simulación y que te haya ayudado a entender mejor la relación entre los decimales y sus fracciones generatrices.
¡Me encantaría saber tu opinión! ¿Qué te pareció la simulación? ¿Hubo algo que te sorprendió o te ayudó a comprender mejor un concepto? ¿Qué tipo de decimal te resultó más interesante?
¡Deja tu comentario abajo! Tus ideas nos ayudan a seguir creando herramientas y recursos que te faciliten el aprendizaje. ¡Anímate a compartir tu experiencia!»
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
1.Halla la fracción generatriz de cada una de las siguientes expresiones decimal exacto.
| a) | 3,4 | d) | 33,58 | g) | 245,7 |
| b) | 0,224 | e) | 7,091 | h) | 34,922 |
| c) | 3,09 | f) | 0,0003 | i) | 5,89 |
2.Determina la fracción generatriz de cada uno de los siguientes decimales periódicos puros.
| a) | 3,33… | d) | 3,5858… | g) | 1,5… |
| b) | 0,2… | e) | 0,777… | h) | 0,9… |
| c) | 90,11… | f) | 12,34… | i) | 1,802… |
3.Calcula la fracción generatriz de cada uno de los siguientes decimales periódicos mixtos.
| a) | 0,133… | d) | 3,5877… | g) | 0,122… |
| b) | 3,011… | e) | 0,922… | h) | 0,033… |
| c) | 2,211… | f) | 5,2333… | i) | 81,0411… |
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión
