¿Alguna vez te has preguntado por qué en el colegio insisten tanto con fracciones y expresiones decimales, si en tu día a día lo que ves son precios, medidas, porcentajes o números en la pantalla del celular?
Aunque no lo notes, estas dos formas de representar cantidades están en casi todo lo que usas: cuando divides el costo de una pizza con tus amigos, revisas la batería del teléfono, calculas cuánto te falta para completar un nivel en un videojuego o comparas tiempos, distancias o porcentajes en actividades que haces a diario. Cuando aprendes a transformar fracciones en decimales y a ubicarlos en la recta real, no solo estás resolviendo ejercicios: estás entendiendo cómo funcionan realmente los números que ves y usas todo el tiempo.
Expresiones decimales
| La expresión decimal se obtiene cuando se divide el numerador entre el denominador de una fracción. |
¿Por qué es importante convertir fracciones a expresiones decimales?
Es importante porque permite comparar, interpretar, graficar y facilitar operaciones matemáticas.
Por ejemplo, piensa en esto: ¿cuál te resulta más fácil de entender a simple vista la fracción o la expresión decimal?$$\frac{15}{4}=3,75$$
La mayoría diría que 3,75 porque es un número que puedes visualizar y comparar al instante.
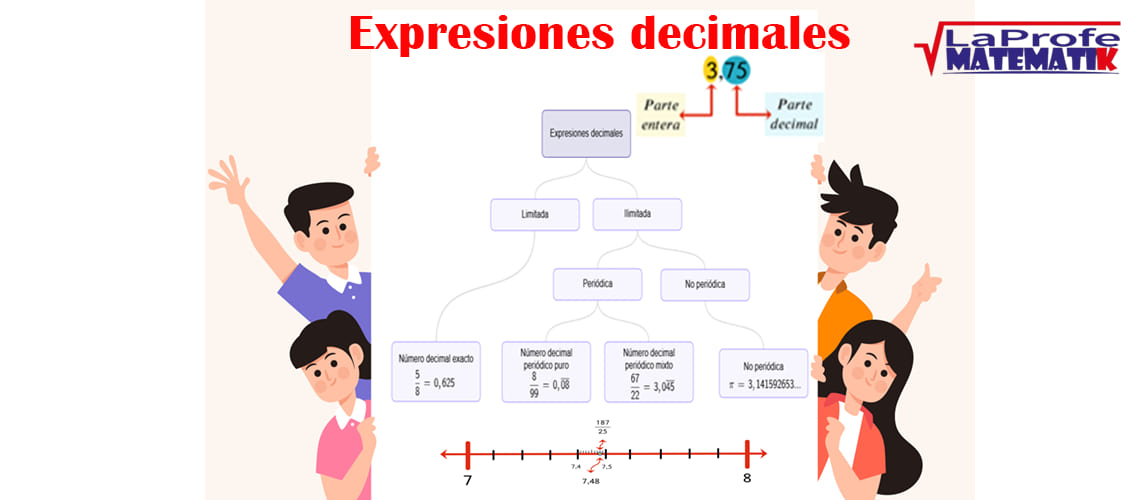
Toda expresión decimal posee dos partes:
1. Una entera (a la izquierda de la coma decimal) y
2. Otra decimal (a la derecha de la coma)
Conversión de fracciones a expresión decimal
Existen dos formas para transformar una fracción a un número decimal, todo depende si son fracciones decimales o fracciones comúnes.
Fracciones Decimales: ¡La forma rápida!
Para convertir fracciones decimales, el proceso es muy sencillo y rápido: solo debes mover la coma decimal hacia la izquierda según la cantidad de ceros que tenga el denominador.
Procedimiento
1. Escribe primero el numerador. Es decir, el número que aparece en la parte superior de la fracción.
2. Observa cuántos ceros tiene el denominador (el número de abajo). Por ejemplo, 10 tiene un cero; 10 000 tiene cuatro, y así sucesivamente.
3. Desplaza la coma decimal. Hacia la izquierda tantas posiciones como ceros tenga el denominador. Ese movimiento convierte la fracción en su equivalente decimal.
Recuerda
Todo número entero tiene una coma decimal «oculta» al final; por ejemplo, 24 es equivalente a 24,0.
Si necesitas mover la coma más lugares de los que tiene el número, simplemente añade ceros a la izquierda para completar el desplazamiento sin alterar su valor.
Ejemplo
Transforma 253/100 a decimal.
Fracciones Comunes (No Decimales): ¡A Dividir se ha Dicho!
Cuando se trata de fracciones comunes (aquellas que no tienen potencias de 10 en el denominador), debes dividir el numerador y el denominador hasta obtener un cociente decimal si es necesario.
Ejercicio resuelto
Convertir las siguientes fracciones a expresión decimal.
$$\frac{3}{5}; \frac{15}{16}; \frac{75}{6}\;\;y\:\;\frac{5}{7}$$
Solución:
Representación gráfica de un número decimal
Es muy importante graficar las expresiones decimales en la recta numérica (a veces también llamada recta real). ¿Por qué? Porque esto permite visualizar de forma precisa su ubicación.
¿Qué ventajas ofrece?
1. Te ayuda a ver dónde “viven” los decimales entre los números enteros.
Cuando los ubicas en una recta, entiendes que números como 1,5 no están aislados, sino que se encuentran exactamente a medio camino entre 1 y 2. Esto hace que el número tenga más sentido, porque lo puedes visualizar.
2. Hace mucho más fácil comparar decimales.
Al ponerlos en la recta real, es evidente cuál número está más a la derecha (y por tanto es mayor). En lugar de confundirte con cifras decimales largas, solo miras su posición y listo: la comparación se vuelve visual e intuitiva.
Procedimiento para graficar
Para graficar expresiones decimales en la recta real debes seguir los siguientes pasos:
1. Ubicar en la recta real la parte entera de la expresión decimal.
2. Localiza la parte decimal del número, tomando en cuenta la cantidad de cifras decimales que tenga.
2.1 Si el número posee una cifra decimal (por ejemplo, 5,4), divide el segmento entre los enteros 5 y 6 en 10 partes iguales.
2.2 Si tiene dos cifras decimales (por ejemplo, 5,45), vuelve a dividir en 10 partes iguales entre 5,4 y 5,5.
Continúa este proceso tantas veces como cifras decimales tenga el número, para acercarte con mayor precisión a su valor en la recta numérica.
Ejemplo
Ubicar en la recta real la fracción 187/25 = 7,48
Solución
1. Ubicar en la recta real la parte entera (entre 7 y 8) y dividir en 10 partes iguales la distancia entre los enteros para localizar la primera parte decimal.
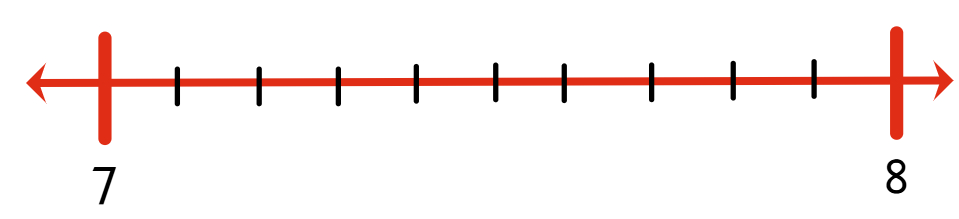
2. El decimal 7,48 está ubicado entre 7,4 y 7,5.
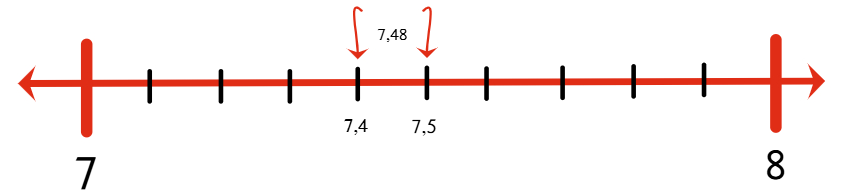
3. Dividir el segmento de 7,4 y 7,5 en 10 partes iguales para obtener la posición de las centésimas.
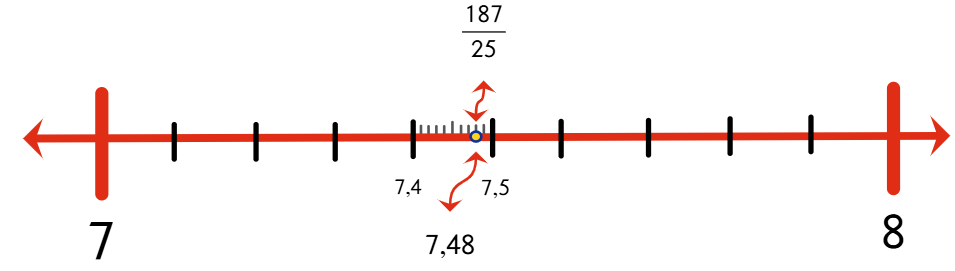
Clasificación de las expresiones decimales
Las expresiones decimales se clasifican de dos formas denominadas: limitada e ilimitada.
Observa la siguiente imagen:
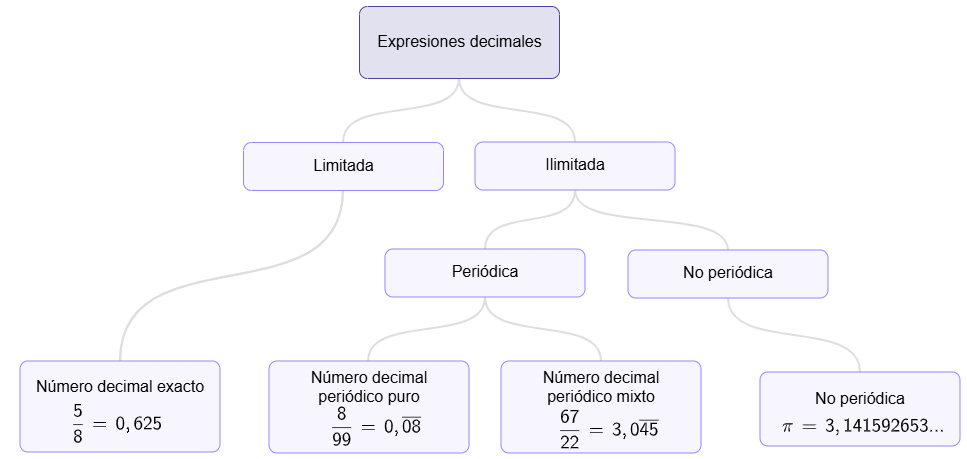
Limitada
Son decimales finitos (tiene un finalización) debido a que en el resto de la división se obtiene cero (0).
Estos tipos de decimales se les llaman Número Decimal exacto.
Por ejemplo:$$2,3\;;\; 5,034\;;\;0,625$$
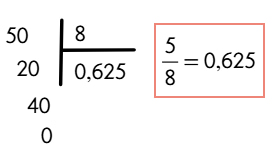
| 😯 Curiosidad: Estos tipos de decimales se pueden transformar en fracciones decimales. |
Ilimitada
Son decimales infinitos (no tiene fin), ya que por más que se continúe el proceso de la división, el resto siempre será un número distinto a cero (0).
La expresión decimal ilimitada se divide en: Periódica y No periódica.
Periódica
Son clasificados en dos tipos de decimales llamados: Periódico Puro y Periódico Mixto.
Número Decimal Periódico Puro
Se les llama periódico puro porque en el cociente surgen dígitos repetitivos consecutivamente, y es pura ya que el periodo comienza inmediatamente después de la coma.
A ese grupo de dígitos se denota con un arco o una pequeña línea colocada en la parte superior de ellos.
Ejemplo:
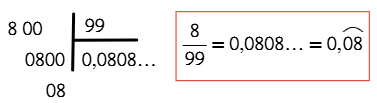
Otros ejemplos:
¿Cómo se obtienen los números decimal periódico puro?
Se obtiene a partir de fracciones irreducibles donde sus denominadores son números primos distintos a dos (2) y cinco (5).
¿Cómo se construyen?
Inicia con una fracción irreducible con denominadores diferentes de cero como 3, 7, 11, 13, etc., luego realizas la división del numerador entre el denominador.
Por ejemplo: transforma la siguiente expresión racional a decimal.
¡Qué fácil es hallar estos tipos de decimales ilimitados!
| 😯 Curiosidad:Cuando una fracción no produce un decimal terminado, sino uno infinito, ese decimal siempre termina repitiéndose. Es decir, todas las expresiones decimales infinitas que vienen de una fracción a/b son periódicas. Además, el bloque que se repite (el período) nunca puede ser más largo que b−1. Esa es la longitud máxima que podría tener la repetición. |
Por ejemplo:
El denominador es 7, se aplica b-1 para conocer la mayor longitud posible del periodo.
7-1=6 es decir, que el decimal repetitivo puede tener hasta 6 cifras en su ciclo como máximo.
Número Decimal Periódico Mixto
Se les denomina mixta porque la parte decimal está compuesta por dígitos no periódicos y dígitos periódicos. Al grupo de decimales no periódicos se les llama anteperiodo. Ejemplo:
Donde el periodo es 67 y el anteperiodo es 34.
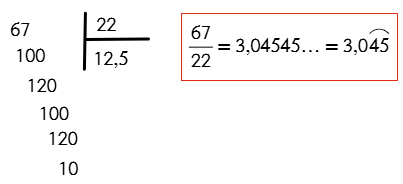
¿Se puede construir un número decimal periódico mixto?
Sí, se construye con fracciones irreducibles cuyos denominadores es la combinación de cualquier número primo (distinto a 2 ó 5) con 2 o con 5.
¿Cómo se construye?
Crea una fracción irreducible, escribe un número en el numerador, luego combina dos factores primos (el primero distinto a 2 ó 5 y el segundo selecciona el 2 ó 5) y lo ubicas en el denominador. Observa los siguientes ejemplos:
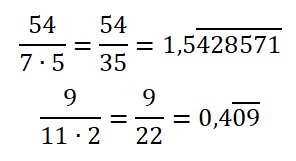
No Periódica
Son expresiones decimales infinitos que no poseen un patrón periódico de sus cifras.
¿Quieres practicar más con un tutor Fracciones y expresiones decimales?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
1.Hallar expresiones decimales de las siguientes fracciones (máximo 4 decimales) y clasifícalas según el resultado en: número decimal exacto, periódicas puras o periódicas mixtas.
| a) | 95/100 | d) | 23/10000 | g) | 2/7 |
| b) | 5/3 | e) | 71/34 | h) | 5/100 |
| c) | 100/100 | f) | 28/1 000 | i) | 1/4 |
2.Representa en una recta numérica y ordena de forma descendente las siguientes expresiones:
| a) | 5/10 | c) | ¾ | e) | -3/5 | g) | -1/2 |
| b) | 0,3 | d) | 2,5 | f) | -0,3 | h) | 0,6 |
3.Construye 5 fracciones que generen expresiones decimales periódicas. Justifique su respuesta.
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión