¿Sabías que las funciones están presentes en muchos aspectos de nuestra vida diaria? Aunque no siempre nos demos cuenta, constantemente utilizamos relaciones que pueden expresarse como funciones.
¿Sabías que las funciones están presentes en muchos aspectos de nuestra vida diaria? Aunque no siempre nos demos cuenta, constantemente utilizamos relaciones que pueden expresarse como funciones.
- Cuando expresamos nuestras ideas o emociones, por ejemplo: “si estudio más, obtengo mejores resultados”, estamos estableciendo una relación causa–efecto, muy similar a una función.
- En el consultorio médico, cuando el doctor nos entrega un resultado de un estudio, ese valor depende directamente de una variable, como la presión arterial, la glucosa o la edad del paciente.
- Al viajar en carro, la cantidad de kilómetros que podemos recorrer está en función de la gasolina que se le agregue al tanque: más gasolina, más distancia.
- En la economía familiar también las usamos: el costo total de un producto depende del número de unidades compradas.
- Incluso en actividades sencillas, como preparar jugo, el tiempo que tardamos depende de la cantidad de frutas que tengamos que pelar o licuar.
En pocas palabras: cada vez que una cantidad depende de otra, estamos frente a una función.
Definición de funciones
Una magnitud “y” se llama función de la variable “x”, si a cada valor de “x” corresponde, a cierta ley de correspondencia, un único valor determinado de “y”. En este caso se dice que “y es función de x” y esto se puede expresar de la siguiente manera:
$$y=f(x)$$
Elementos de una función
En una función el conjunto de partida “X” es el dominio conocido también como las preimágenes y se escribe: Dom f.
Todo el conjunto de llegada “Y” es llamado codominio o contradominio y se escribe: Cod f.
El rango, también llamado recorrido, es el conjunto formado por todos los elementos del codominio que efectivamente son imágenes de algún valor del dominio.
El rango se escribe: Rg f
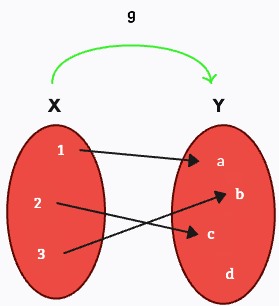
Ejemplo.
Sean:
\(X = \{1, 2, 3\}\) y
\( Y = \{a, b, c, d\} \)
si \(g:X \rightarrow Y\) es una función de \(X\) en \(Y\)
Identifica los siguientes elementos de la función g.
- Conjunto de partida (dominio).
- Conjunto de llegada (codominio).
- Elementos del conjunto de partida (preimágenes).
- Elementos del conjunto de llegada.
- Rango o imágenes.
Solución
Conjunto de partida:
\( Dom(g)=X \)
Conjunto de llegada:
\( Cod(g)=Y \)
Elementos del conjunto de partida:
\( X = \{ 1, 2, 3 \} \)
Elementos del conjunto de llegada:
\( Y = \{ a, b, c, d \} \)
Rango:
\(Rg(g)= \{ a, b, c \} \)
Diferentes maneras de expresar funciones
Una función f de un conjunto “ X ” en otro conjunto “ Y ” es una correspondencia que asigna cada elemento \(x \in X\) un sólo elemento \(y \in Y\)
Los elementos \(y \in Y\) son las imágenes de x bajo f
Las funciones generalmente se escriben con letras minúsculas como f, g, h, . . . y se expresan de la siguientes maneras:
\(f: X \rightarrow Y\) \(x \rightarrow f(x)\) \( X \overset{f}{\rightarrow} Y\)
Su significado indica que f manda x a y o que f manda x a f (x) . La expresión f (x) significa la imagen de x.
Por ejemplo, f(x) = \(x^{2}\)
f manda x a x2 , es decir, que cada pareja ordenada se expresa \((x, x^{2})\).
El valor de la función:
\(f(x)\) cuando \(x = 2\) es \(f(2) = 2^{2} = 4\) y el par ordenado es \((2, 4)\).
Es o no función
Una función es una regla que asigna cada elemento del conjunto de partida un elemento del conjunto de llegada, es decir que toda función es una relación, pero no toda relación es una función.
¿Cómo conocer si es una función?
Se debe tener en cuenta las siguientes condiciones:
- Es función cuando cada elemento del conjunto de partida se relaciona únicamente con una imagen.
- No es función, sí al menos un elemento del conjunto de partida no está relacionado.
- No es función, cuando un elemento del conjunto de partida posee más de una imagen.
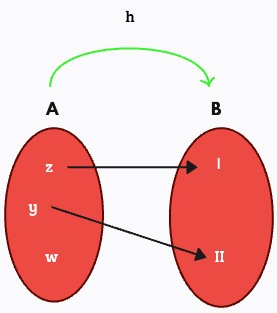
¿Cómo saber si es función en un diagrama sagital?
En la figura a continuación, la relación f es función debido a que cada elemento del conjunto de partida A sólo se relaciona con un elemento del conjunto de llegada B.
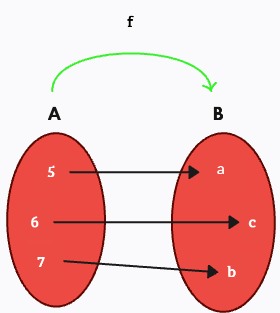
La relación g , No es función ya que los elementos 5 y 7 del conjunto de partida A poseen más de una imagen en el conjunto de llegada B.
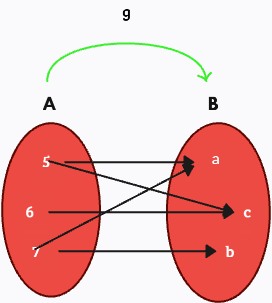
La relación h, No es función debido que el elemento w del conjunto de partida A no posee imagen.
¿Cómo saber si es función una expresión algebraica?
Para determinar si una expresión algebraica representa una función, primero se construye la tabla de valores y se elabora su gráfica. Luego se aplica la prueba de la línea vertical: si al trazar una línea vertical esta corta a la gráfica en un solo punto, se trata de una función; en caso contrario, no lo es.
Ejemplo: Es función la siguiente expresión
$$f(x) = \pm \sqrt{x+2}$$
Paso#1: Tabla de valores.
| x | y |
| -3 | No existe |
| -2 | 0 |
| -1 | +/- 1 |
| 0 | $$\pm \sqrt{2}$$ |
| 1 | $$\pm \sqrt{3}$$ |
| 2 | +/- 2 |
| 3 | $$\pm \sqrt{5}$$ |
Paso#2: Gráfica y trazado de línea vertical.
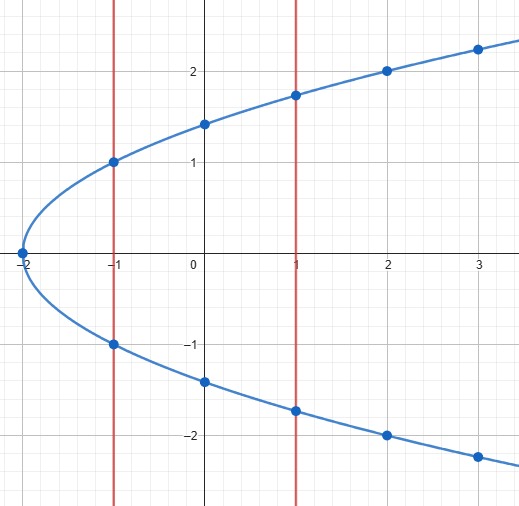
Como conclusión la expresión dada \(f(x) = \pm \sqrt{x+2}\)
No es función ya que al aplicar la prueba de la línea vertical toca dos puntos en la curva.
Representación de funciones
Existen muchas formas para representar a las funciones, entre estas representaciones están las de:
- Representación verbal. Se realiza por medio de una expresión explícita de la regla que asigna a cada elemento del conjunto de partida o dominio, con su correspondiente imagen. Por ejemplo «El doble de un número»
- Representación algebraica. Es cuando se expresa a través de una fórmula. Por ejemplo f ( x ) = 2x
- Representación en tabla de valores. Se refiere a dos filas o dos columnas, en la primera fila o la primera columna se distribuye los valores de la variable independiente “ x ” y en la segunda fila o columna los valores de la variable dependiente “ y ”. A continuación una tabla de valores de dos columnas.

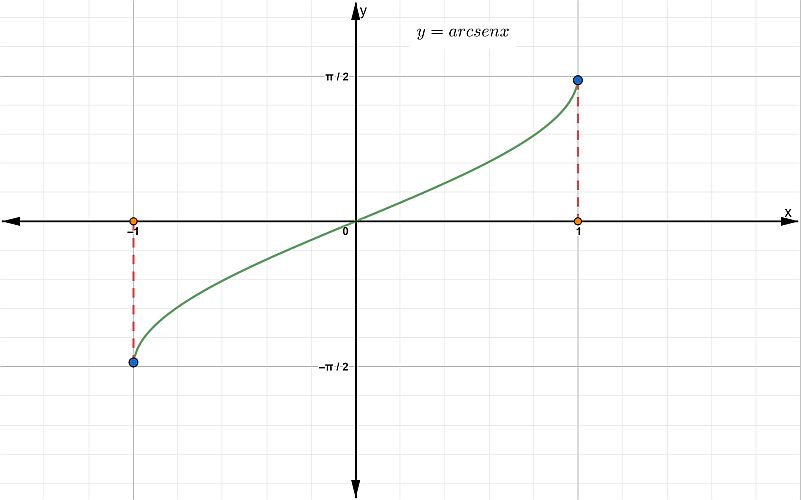
- Representación gráfica. Es obtenida al ubicar en el plano cartesiano un par ordenado ( x , y ), proveniente de la tabla de valores, al representar cada par ordenado se obtiene la siguiente gráfica.
 |
Ejemplo de funciones en la vida diaria
Un ejemplo muy fácil de funciones es cuando vamos a comprar cebollas al mercado por el precio de $1000 el kilogramo, entonces la ley que determina el valor de la cebolla es la siguiente expresión matemática:
$$y = 1000x$$
donde: \(y = \text{costo}\) y \(x = \text{peso (kg)}\)
Ahora observe la compra que realizaron 6 personas, cada pago que efectuaron está en función a las cantidades de cebollas que seleccionaron, dicho en otras palabras cada costo de pago se ejecutó en función al peso.
| x = peso en kilogramos | y = costo de la cebolla |
| 0,875kg | $$y = 1000 \cdot 0.875 kg=875$$ |
| 0,75kg | $$y=1000 \cdot 0.75 kg=750$$ |
| 0,432kg | $$y = 1000 \cdot 0.432 kg=432$$ |
| 0,255kg | $$y = 1000 \cdot 0.255 kg=255$$ |
| 1,957kg | $$y = 1000 \cdot 1.957 kg=1957$$ |
| 2,540kg | $$y = 1000 \cdot 2.540 kg=2540$$ |
La ley de correspondencia que determina el precio de las cebollas en función al peso en palabras sería de la siguiente manera:
«Para determinar el precio de las cebollas es necesario multiplicar el peso de las cebollas por el valor de la misma en este caso $ 1000»
Variables dependientes e independientes
Las variables dependientes dependen de los valores de las variables independientes, la variable independiente es conocida también como la Causa y la variable dependiente como Efecto. La variable independiente es “x” y la dependiente es “y”.

La variable independiente “x” es aquella que se controla o se elige libremente. Un ejemplo sencillo lo encontramos en una máquina exprimidora de caña de azúcar: la caña de azúcar representa la variable independiente, mientras que el jugo obtenido al exprimirla corresponde a la variable dependiente “y”. Observa la imagen:
Otro ejemplo se presenta al construir una tabla de valores: asignamos distintos valores a la variable independiente “x”, y en consecuencia, la variable dependiente “y” cambia de acuerdo con dichos valores.
Finalmente llamaremos a las variables de la siguiente manera:
x= variable
y= función
Función real de variable real
Se llaman así cuando la variable y la función están definidas en el conjunto de los números reales
la función:
f : A → ℜ
Donde:
ℜ = Conjunto de los números reales
A ⊆ ℜ
Actividades
I.Dado el conjunto M=\(\{-2, 0, 2, 3, 4\}\) y la ley de correspondencia:
$$f(x)=x^{2}$$
Determine:
- El conjunto N.
- Escriba en pares ordenados cada relación.
- Represente en un diagrama sagital.
- Hallar el dominio, codominio y rango.
II.Grafique las siguientes funciones:
Y determinar:
- Dominio.
- Rango.
- Codominio.
- Si es o no función
III.Hallar los valores numéricos de cada función:
| $$f(x) = 2^{x}$$ | $$f(2); f\left(-\frac{1}{2}\right); f(0)$$ |
| $$f(x) = -\sqrt{x+3}$$ | $$f(0); f\left( \frac{1}{3} \right); f(6)$$ |
| $$f(t) = \sqrt{z} + 6$$ | $$f(49); f(4); f\left( \frac{4}{9} \right)$$ |
IV.Representar por medio de un diagrama sagital la siguiente función, a partir de sus pares ordenados:
![]()
V.Determine en cada caso si el conjunto de pares ordenados corresponde a una función del conjunto X en el conjunto Y
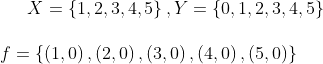 |
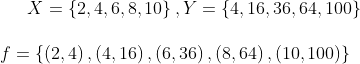 |
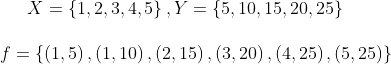 |
VI.Determine las imágenes \(f(1); \, f(-2); \, f(g+10)\) mediante la función \(f(x) = 5x – 3\)