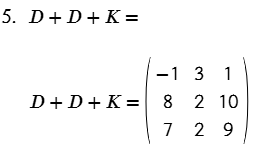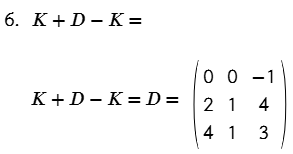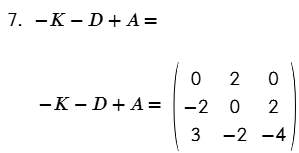¿Sabes cómo las Matrices transforman tus fotos y videojuegos? No son solo tablas de números; las Matrices son el lenguaje secreto de la tecnología digital. Cada vez que aplicas un filtro en Instagram o TikTok, estás usando Matrices sin darte cuenta. Una imagen es, en esencia, una gran Matriz de píxeles, y los filtros son pequeñas Matrices de convolución que aplican cálculos para cambiar el color o el brillo.
¿Sabes cómo las Matrices transforman tus fotos y videojuegos? No son solo tablas de números; las Matrices son el lenguaje secreto de la tecnología digital. Cada vez que aplicas un filtro en Instagram o TikTok, estás usando Matrices sin darte cuenta. Una imagen es, en esencia, una gran Matriz de píxeles, y los filtros son pequeñas Matrices de convolución que aplican cálculos para cambiar el color o el brillo.
En los videojuegos, las Matrices de transformación son la clave: ellas calculan cómo rotar y mover los objetos 3D en la pantalla. Al aprender Matrices, no solo entiendes un concepto matemático; ¡estás descubriendo cómo se programan los efectos visuales, los tipos de datos y las operaciones que dan vida a tu mundo digital!
Matrices
| Son arreglos rectangulares compuesto por números o funciones organizados en fila (horizontal) y columna (vertical). |
Características de la matriz
Una matriz está conformada por las siguientes características:
- Se denotan con una letra mayúscula como:
A, B, C, D, …, etc.
- Utilizan paréntesis ( ) o corchetes [ ] para encerrar a los elementos de la matriz.
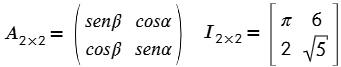
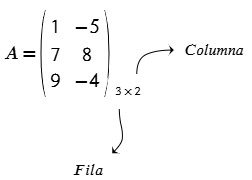
- Dimensión u orden es el tamaño de la matriz. Ejemplo: 3 x 2 el 3 significa la cantidad de filas y el 2 la cantidad de columnas.
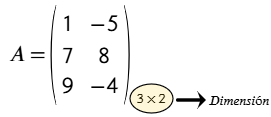
- Cada uno de los números o funciones que componen a la matriz se llama elemento.
 Los elementos se denotan con una letra minúscula y con un subíndice, el primero indica la fila y el segundo la columna. Como:
Los elementos se denotan con una letra minúscula y con un subíndice, el primero indica la fila y el segundo la columna. Como:
aij , bij ,…, etc.
aij se lee “a sub ij”
Observa los elementos de la matriz A2×3 relacionándola con una matriz genérica.

- Cuando una matriz posee la misma cantidad de filas y columnas, es decir, si m = n se le da el nombre de matriz cuadrada.

- Si m es distinto a n se dice que es una matriz rectangular.
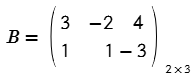
- Una matriz que posee una sola fila o una sola columna se les llama vector fila o vector columna, respectivamente.

Particularidades de las matrices cuadradas
 Las matrices cuadradas son aquellas que tienen igual número de filas que de columnas, es decir, en las que m = n.
Las matrices cuadradas son aquellas que tienen igual número de filas que de columnas, es decir, en las que m = n.
Una matriz con n filas y n columnas es una matriz cuadrada.
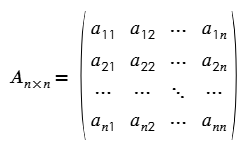
- Elementos principales. En una matriz cuadrada los elementos principales son aquellos que poseen los dos subíndices iguales, ejemplo: a11, a22, a33, a44, …, ann.
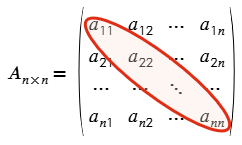
- Diagonal principal o mayor. Está formado por los elementos principales.
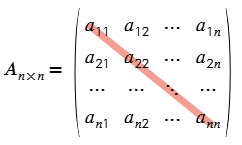
- Traza. Es la suma de los elementos de la diagonal principal. Denotado como tr( ).
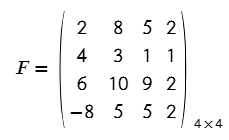
$$tr(F)=2+3+9+2$$
$$tr(F)=15$$
- Diagonal secundaria. Es la otra diagonal formada por los elementos que poseen subíndices que suman n + 1.
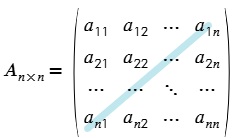
- Elementos conjugados. Son aquellos elementos que poseen el mismo subíndice pero de forma inversa. Ejemplo: a31 y a13.
Los elementos conjugados son simétricos con respecto a la diagonal principal.
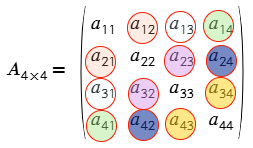
- Matriz diagonal. Es una matriz cuadrada donde los elementos de la diagonal principal son distintos de cero.

- Matriz escalar. Es una matriz diagonal donde sus elementos principales son iguales.

- Matriz unidad o identidad. Es una matriz escalar donde sus elementos principales son iguales a uno.

- Matriz nula. Es una matriz que tiene todos sus elementos son iguales a cero.
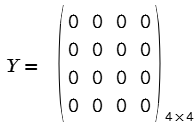
- Matriz triangular superior. Es una matriz cuadrada donde todos sus elementos que se encuentren en la parte inferior de la diagonal principal son iguales a cero.
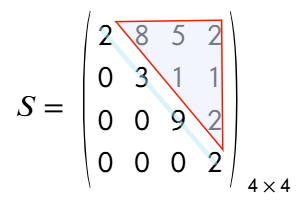
- Matriz triangular inferior. Todos los elementos ubicados en la parte superior de la diagonal principal son iguales a cero.
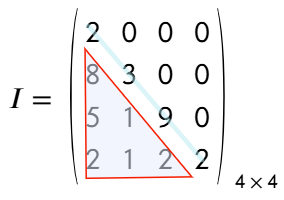
Tipos de matrices
 Las matrices se clasifican según:
Las matrices se clasifican según:
- Dimensiones.
- Filas ( 1 x n ).
- Columna ( m x 1).
- Rectangular ( m x n, con m distinto n ).
- Cuadrada ( n x n ).
- Valores de sus elementos.
- Nula (todos ceros).
- Diagonal.
- Escalar.
- Identidad.
Aplicación: La matriz nula puede presentarse en cualquier dimensión, mientras que la diagonal, la escalar y la identidad corresponden únicamente a matrices cuadradas.
- Posición de ceros.
- Triangular superior.
- Triangular inferior
Aplicable únicamente en el caso de matrices cuadradas.
- Transformaciones y propiedades.
- Traspuesta ( AT )
- Simétrica ( A = AT )
- Antisimétrica ( A = -AT )
- Inversa ( A-1 )
- Ortogonal ( AT = A-1 )
- Semejante ( B = P-1AP )
Aplicación: La traspuesta puede definirse para cualquier matriz, mientras que las demás corresponden únicamente a matrices cuadradas.
Matriz traspuesta: Se obtiene al intercambiar las filas por las columnas de una matriz. La traspuesta de una matriz A se denota como AT. Si la matriz original tiene orden 𝑚 × 𝑛, entonces su traspuesta tendrá orden 𝑛 × 𝑚.
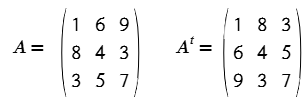
Matriz simétrica: Es una matriz cuadrada que coincide con su traspuesta, es decir, 𝐴 = 𝑇.
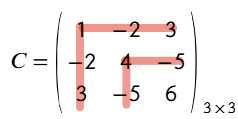
Matriz antisimétrica: Es una matriz cuadrada en la que los elementos equidistantes respecto a la diagonal principal son opuestos entre sí, y todos los elementos de la diagonal principal son nulos.

Operaciones elementales con matrices
Las operaciones con matrices que se tratará en este post son: suma de matrices, multiplicación de un escalar por una matriz, diferencia y multiplicación de matrices.
Suma de matrices
 Para sumar dos o más matrices deben poseer el mismo orden, es decir, la misma cantidad de filas y columnas.
Para sumar dos o más matrices deben poseer el mismo orden, es decir, la misma cantidad de filas y columnas.
Para realizar esta operación se deben sumar los elementos que ocupan la misma posición en las matrices.
Diferencia de matrices
La resta de dos matrices se define como: A – B = A + (-B), donde -B es la matriz opuesta de B. Es decir, restar matrices es sumar la primera con la segunda cambiada de signo.
Ejemplo. Dada las matrices A, D, K. Determine las siguientes operaciones.
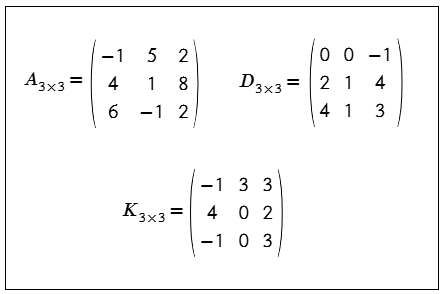
- A + D + K
- A + K – D
- A – D – K
- D – K + A
- D + D + K
- K + D – K
- –K – D + A
- –K + D – A
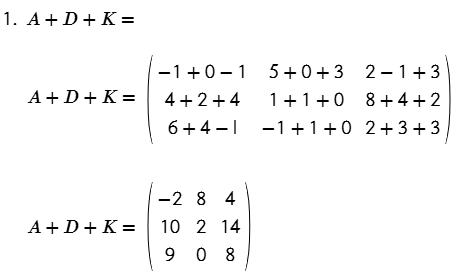
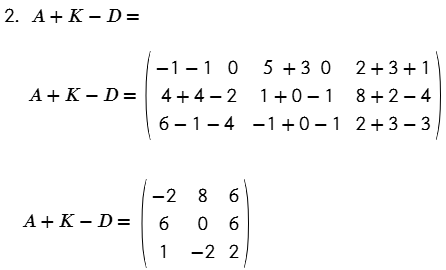
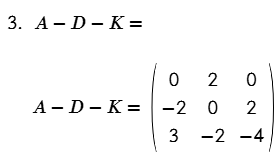
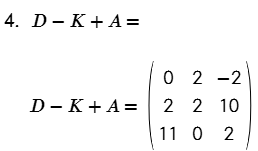
Multiplicación de un escalar por una matriz
 El producto de un escalar por una matriz es la matriz que se obtiene al multiplicar cada elemento de la matriz por el escalar.
El producto de un escalar por una matriz es la matriz que se obtiene al multiplicar cada elemento de la matriz por el escalar.
Ejemplo. Determinar 2A + 3B
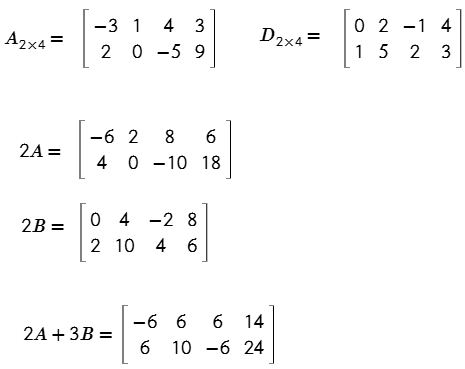
Producto de matrices
Antes de multiplicar dos matrices es necesario verificar que:
- El número de columnas de la primera coincida con el número de filas de la segunda.
¿Cómo puedo comprobar, de manera sencilla, si dos matrices son multiplicables?
Para saber si dos matrices pueden multiplicarse, debes comparar su orden: si el número de columnas de la primera matriz (𝑆) coincide con el número de filas de la segunda (𝐼), entonces la multiplicación está definida.
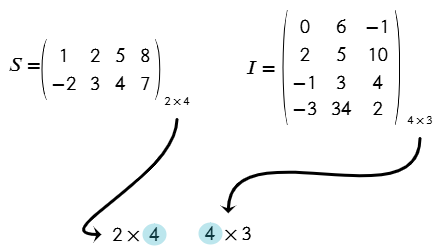
Esto quiere decir que la matriz S puede multiplicarse con la matriz I.
¿Cuántas filas y columnas tendrá el producto de dos matrices?

Para determinar el número de filas y columnas del producto de dos matrices, se toma el número de filas de la primera matriz y el número de columnas de la segunda. Esa será la dimensión de la matriz resultante. Observa el siguiente ejemplo:
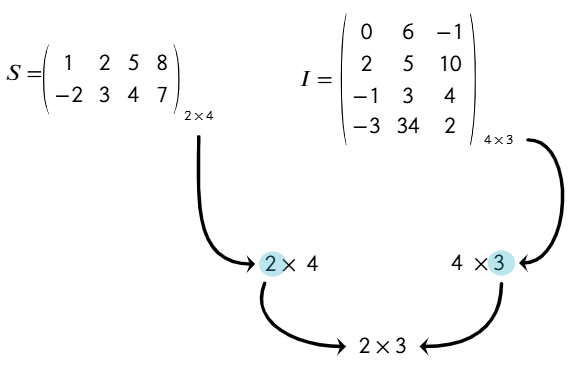
Entonces, la dimensión de la matriz resultante es ( 2 × 3 ).
La escritura del ejemplo es la siguiente:
$$S_{2\times 4}\cdot I_{4\times 3}=M_{2\times 3}$$
Donde:
S tiene m filas y n columnas.
I tiene n filas y p columnas.
El producto M existe y tendrá orden m × p.
¿Cómo puedo multiplicar dos matrices?
Para calcular cada elemento de la matriz producto, debes:
- Seleccionar una fila de la primera matriz 𝐴.
- Elegir una columna de la segunda matriz 𝐵.
- Multiplicar elemento por elemento. Elemento 1 de la fila 𝐴 con el elemento 1 de la columna 𝐵, elemento 2 de la fila 𝐴 con el elemento 2 de la columna 𝐵 y así sucesivamente.
- Sumar todos esos productos.
- Identificar el elemento (ejemplo: a11 = 5) con su valor respectivo y ubicarlo en la posición correspondiente de la matriz.
- Repite el procedimiento con cada fila de 𝐴 y cada columna de 𝐵 hasta completar todos los elementos de la matriz producto.
Ejemplo # 1. Dada las matrices H y G. Determinar H • G.
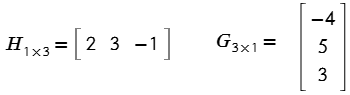
Solución
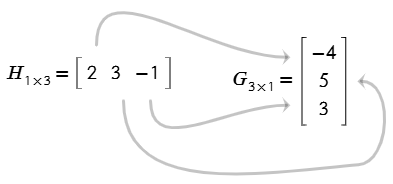
$$H_{1\times 3}\cdot G_{3\times 1}=O_{1\times 1}$$
$$C_{1\times 1}=-8+15-3=4$$
$$\boxed{C_{1\times 1}=[4]}$$
Ejemplo # 2. Determinar A • B.
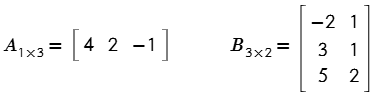
Solución
$$A_{1\times 3}\cdot B_{3\times 2}=C_{1\times 2}$$
$$C_{1\times 2}=\left [ C_{11}\,\, \, C_{12} \right ]$$
Multiplicar la fila (A) con la primera columna (B), para obtener el elemento C11.
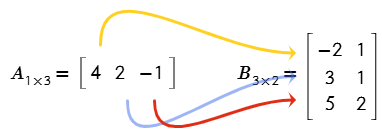
$$C_{11}=-8\,\,+6\,\,-5$$
$$C_{11}=-7$$
Multiplicar la fila (A) con la segunda columna (B), para obtener el elemento C12.
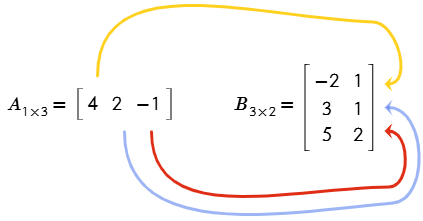
$$C_{12}=4\,+2\,\,-2$$
$$C_{12}=4$$
Matriz producto
$$\boxed{C_{1\times 2}=\left [ -7\,\,\,\,\,4 \right ]}$$
Ejemplo # 3. Determinar el producto de las matrices A y B.
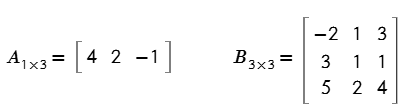
Solución
$$A_{1\times 3}\cdot B_{3\times 3}=C_{1\times 3}$$
$$C_{1\times 3}=\left [ C_{11}\,\, \, C_{12}\,\,\,C_{13} \right ]$$
| $$C_{11}=-8+6-5=-7$$ |
| $$C_{12}=4+2-2=4$$ |
| $$C_{13}=12+2-4=10$$ |
Resultado:
$$C_{1\times 3}=\left [ -7\,\,\,4\,\,\,10 \right ]$$
Ejemplo # 4. Calcular A • B
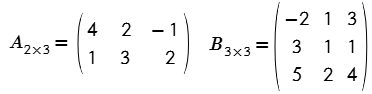
Solución
$$A_{2\times 3}\cdot B_{3\times 3}=C_{2\times 3}$$
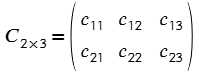
Cálculo de todos los elementos de la matriz C
| $$\textstyle C_{11}=-8+6-5=-7$$ | $$\textstyle C_{21}=-2+9+10=17$$ |
| $$\textstyle C_{12}=4+2-2=4$$ | $$\textstyle C_{22}=1+3+4=8$$ |
| $$\textstyle C_{13}=12+2-4=10$$ | $$\textstyle C_{23}=3+3+8=14$$ |
Al distribuir cada elemento el producto de la matriz es:

Ejemplo # 5. Multiplicar las matrices A y B
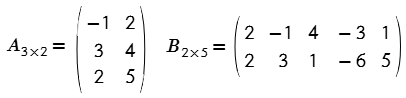
Solución
$$A_{3\times 2}\cdot B_{2\times 5}=C_{3\times 5}$$

Valores de los elementos de la matriz C
| $$C_{11}=(-2+4)=2$$ $$C_{12}=(1+6)=7$$ $$C_{13}=(-4+2)=-2$$ $$C_{14}=(3-12)=2$$ $$C_{15}=(-1+10)=9$$ $$C_{21}=(6+8)=14$$ $$C_{22}=(-3+12)=9$$ $$C_{23}=(12+4)=16$$ $$C_{24}=(-9-24)=-33$$ $$C_{25}=(3+20)=23$$ $$C_{31}=(4+10)=14$$ $$C_{32}=(-2+15)=13$$ $$C_{33}=(8+5)=13$$ $$C_{34}=(-6-30)=-36$$ $$C_{35}=(2+25)=27$$ |
Respuesta

Simulador de producto de matrices
¿Cansados de los errores al multiplicar Matrices a mano? ¡El misterio de filas por columnas se acaba hoy! Llegó el momento de poner a prueba tus conocimientos de una forma visual e interactiva.
Te presento nuestro simulador, tu herramienta para dominar el producto de matrices. Olvídate de los largos cálculos en papel; ahora vas a ver la operación en acción y entender su lógica.
Con el Simulador:
Visualiza el Proceso: Observa paso a paso cómo se combinan filas y columnas, entendiendo por qué el orden es fundamental.
Domina la Compatibilidad: Prueba a multiplicar distintos tamaños de matrices para ver si el producto es posible, ¡al instante!
Este es tu campo de entrenamiento virtual para dominar una habilidad clave en la programación y la ingeniería. ¡Es hora de multiplicar como un profesional!
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
I.Escribe el valor de cada elemento de acuerdo con la siguiente matriz
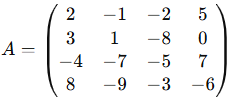

II.Escribe el orden de las siguientes matrices

III.Construye una matriz de acuerdo con las características indicadas
- Matriz simétrica de orden 3×3.
- Matriz antisimétrica de orden 4×4.
- Matriz Triangular superior de orden 3×3.
- Matriz Triangular inferior de orden 4×4 y que tenga a11=a22=a33=a44=5
IV.Hallar el valor de las incógnitas que satisfacen cada igualdad.
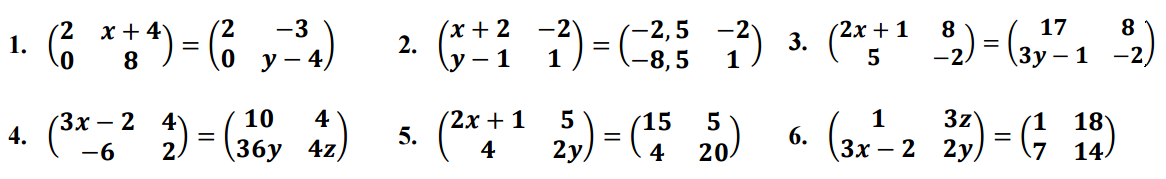
V.Determina la matriz asociada a cada uno de los siguientes de ecuaciones.


VI.Resuelve las operaciones indicadas
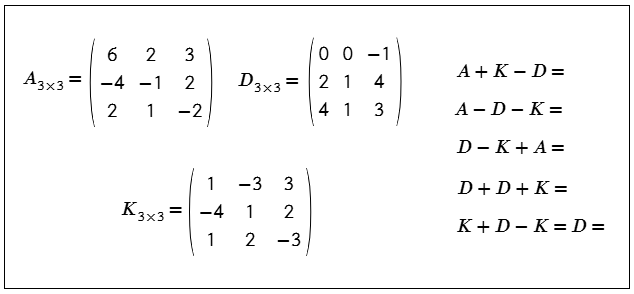
VII.Un empresario estudia el reporte de dos años consecutivos de producción, en miles de toneladas que se muestra a continuación:

- ¿Cómo se puede representar esa información por medio de dos matrices?
- ¿Cuál matriz representa la producción total de ambos años y la diferencia entre el 1° año y 2° año, según zona y producto?
Resultados
I
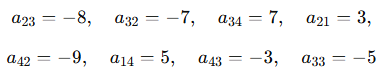
II
- (1×2)
- (2×3)
- (1×3)
- (2×2)
- (3×1)
- (4×3)
- (3×2)
- (4×2)
III
 |
 |
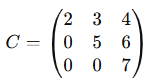 |
 |
IV
x=-7, y=12.
x=-4.5, y=-7.5.
x=8, y=2.
x=4, y=-1/6, z=1/2.
x=7, y=10.
x=3, y=7, z=6.
V.
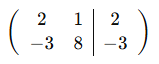 |
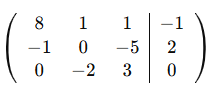 |
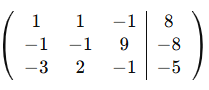 |
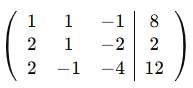 |
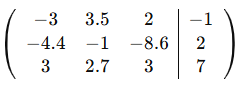 |
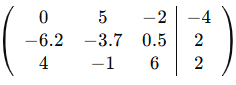 |
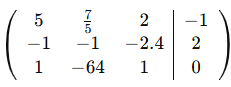 |
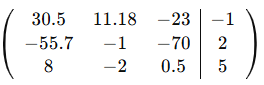 |

 Los elementos se denotan con una letra minúscula y con un subíndice, el primero indica la fila y el segundo la columna. Como:
Los elementos se denotan con una letra minúscula y con un subíndice, el primero indica la fila y el segundo la columna. Como: