¿Sabías que cada vez que tu personaje se mueve, salta o cambia de tamaño en un videojuego estás presenciando transformaciones geométricas en acción? La geometría no vive solo en los libros: es parte esencial del diseño de tus juegos favoritos. Cada traslación que te mueve de un lado a otro, cada rotación que gira la cámara, la reflexión que ves en el agua y la homotecia que hace que un objeto se vea más grande o pequeño en pantalla son transformaciones que hacen que todo se vea y se sienta realista.
¿Qué es una transformación geométrica?
Las transformaciones geométricas es un procedimiento aplicado a una figura dada obteniendo otra denominada imagen.
Clasificación de las transformaciones
Las transformaciones geométricas son muy interesantes ya que por medio de estos procedimientos pueden generarse imágenes congruentes o semejantes.
Los tipos de transformaciones geométricas que generan imágenes congruentes son conocidas con el nombre de:
- Traslación.
- Rotación y
- Reflexión.
La transformación geométrica encargada de crear imágenes semejantes es conocida como Homotecia.
Traslación
| Son transformaciones geométricas encargada del desplazamiento que puede aplicarse a cualquier figura, como un punto, segmento, polígono, cubo, círculo u otra figura tridimensional. Para realizarlo, necesitas conocer los valores h y k. |
Nota: Este post se enfocará en la traslación en el plano cartesiano.
¿Qué representa h y k ?
La traslación es un tipo de transformación que desplaza un punto A (x, y) del plano en otro A´( x + h, y + k ) que es la imagen.
Donde h representa el desplazamiento horizontal y k el vertical en unidades.
¿Qué pasa con h y k al ser positivos o negativos?
Cuando h es positivo, el desplazamiento horizontal (en el eje de las abscisas) es realizado hacia la derecha; pero, si h es negativo, su desplazamiento es a la izquierda.
Cuando k es positivo, el desplazamiento vertical (en el eje de las ordenadas) es hecho hacia arriba; en cambio, si k es negativo, el movimiento es hacia abajo.
¿Cómo debes hacer la traslación?
A continuación, verás dos ejemplos: en el primero se explica cómo trasladar un punto y, en el segundo, cómo trasladar un romboide.
Ejemplo 1. Trasladar un punto
Trasladar el punto D (3,2) tres unidades positiva verticalmente y cuatro unidades positiva horizontalmente.
Procedimiento:
Número 1. Identificar h y k.
h = 4 y k = 3
Número 2. Al trasladar el punto D se transforma en D´
Aplicando: D´( x + h, y + k )
D´ (3 + 4, 2 + 3)
D´ (7,2).
Observa el resultado del traslado del punto D, donde su imagen es D´.

Ejemplo 2. Trasladar un romboide
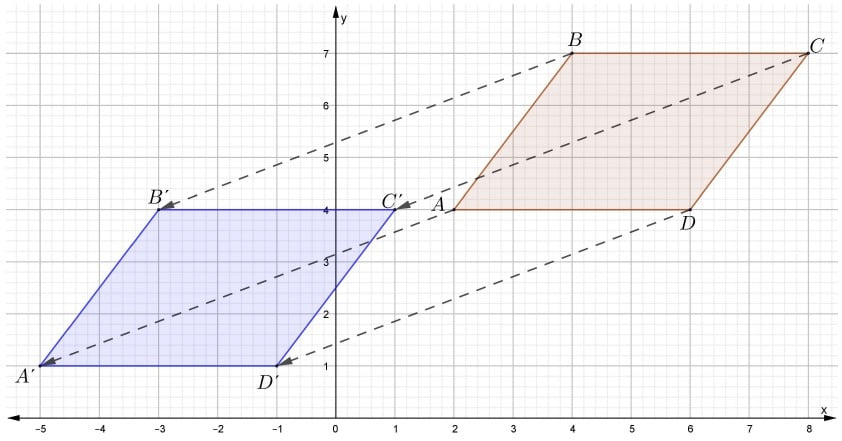
Trasladar el romboide ABCD, -7unidades horizontalmente y -3 unidades verticalmente.
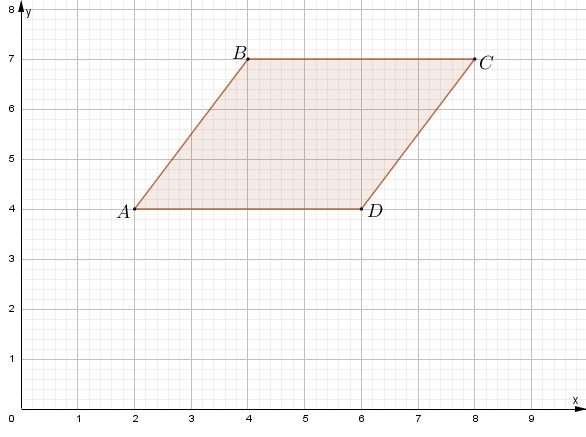
Procedimiento:
Número 1. Valores h y k.
h = -7 y k = -3
Número 2. Determinar la imagen de cada vértice del romboide.
| Figura (vértices del romboide) | ( x – 7, y – 3 ) | Imagen |
| A (2,4) | ( 2 – 7, 4 – 3) | ( -5, 1) |
| B (4,7) | ( 4 – 7, 7 – 3 ) | ( -3, 4 ) |
| C (8,7) | ( 8 – 7, 7 – 3 ) | ( 1, 4 ) |
| D (6,4) | ( 6 – 7, 4 – 3 ) | ( -1, 1 ) |
Rotación
| Son transformaciones geométricas que consiste en girar todos los puntos de una figura alrededor de un punto fijo. Debes poseer dos elementos el centro de rotación y el ángulo. |
¿Cómo realizar la rotación?
A continuación, te presento un ejemplo en el que aprenderás a rotar un romboide, explicado paso a paso. Verás cómo, siguiendo cada indicación, es posible comprender y aplicar este tipo de transformación de manera sencilla y precisa.
Ejemplo. Rotar un romboide
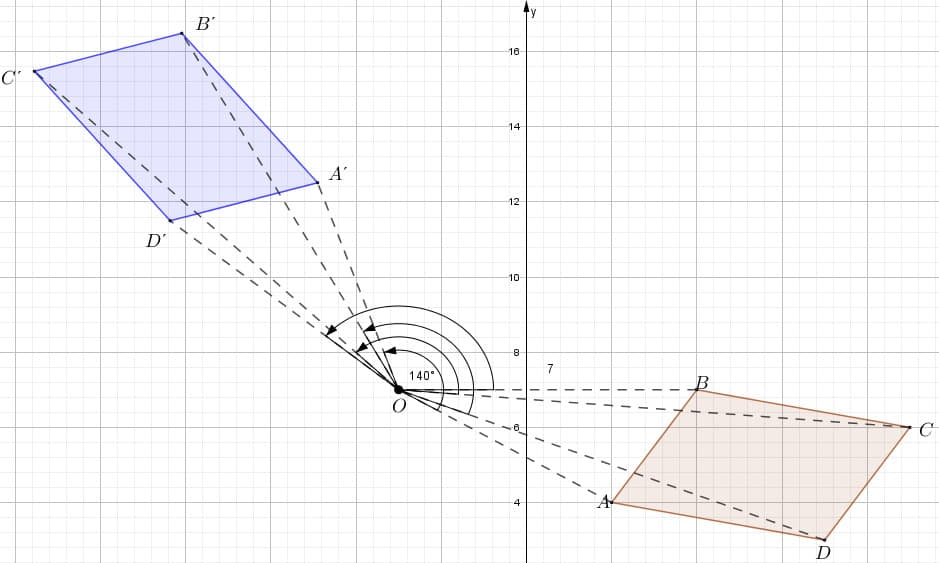
Rote el romboide ABCD a un ángulo de 140° sentido antihorario con centro O.
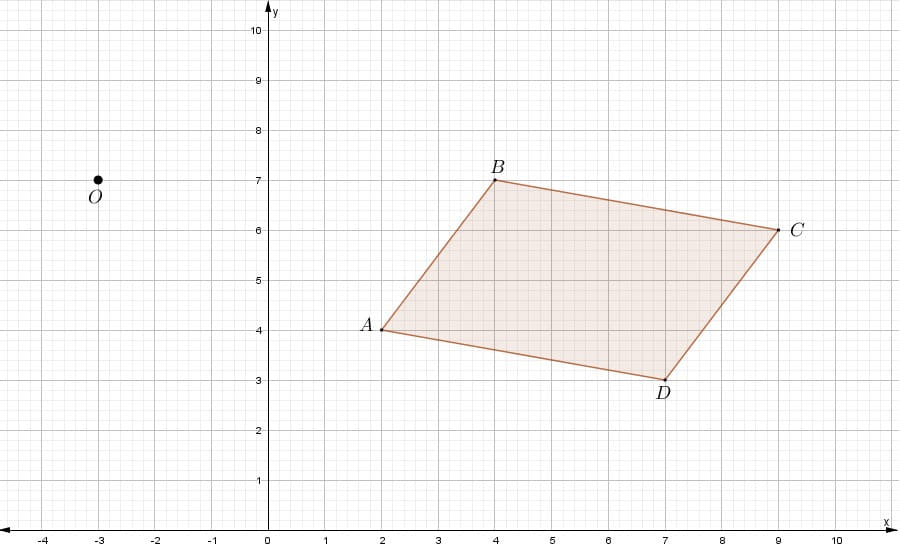
Primero. Unir cada vértice del romboide con el centro O.
Segundo. Rota en sentido antihorario los cuatro segmentos AO, DO, CO y BA a 140° y describe la imagen de cada vértice.
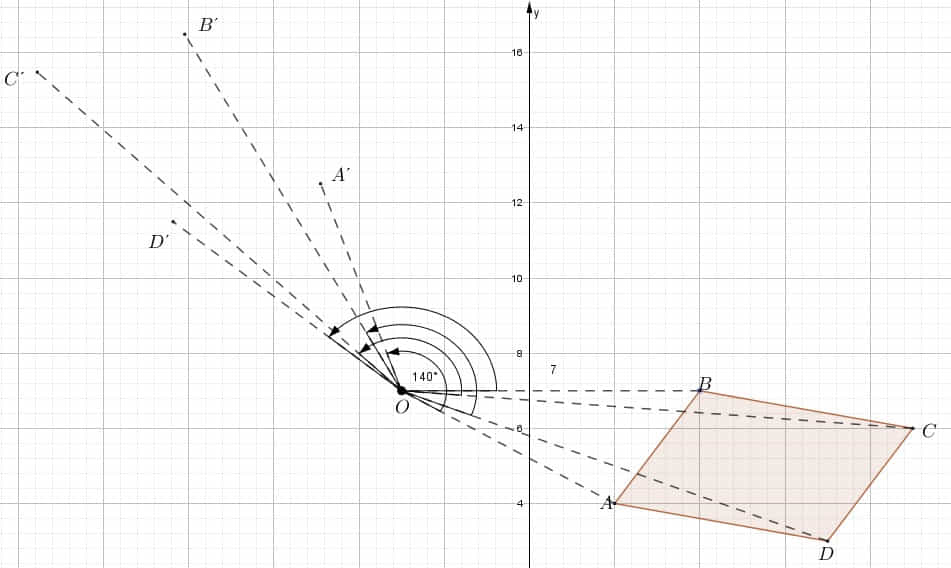
Tercero. Unir los puntos A´, B´, C´ y D´ para formar la imagen del romboide.
Reflexión
| Llamada también simetría axial, este tipo de transformación refleja una figura respecto a una recta denominada eje de reflexión o eje de simetría, generando una imagen con las mismas distancias de la figura al eje. Los elementos para materializar una reflexión son dos el objeto y el eje de simetría (segmento). |
¿Cómo debes realizar una reflexión?
Te voy a mostrar cómo realizar la reflexión de un triángulo, explicada a través de un ejemplo práctico. Paso a paso, descubrirás cómo se transforma la figura y cómo identificar su imagen reflejada de forma sencilla.
Ejemplo. Reflexión de un triángulo
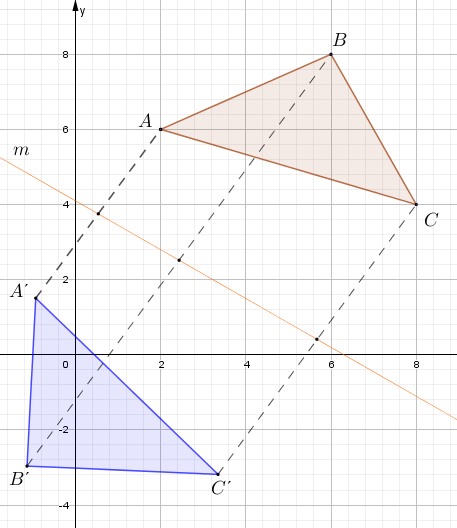
Dado el triángulo ABC y su eje de reflexión m. Encuentre su imagen reflejada.
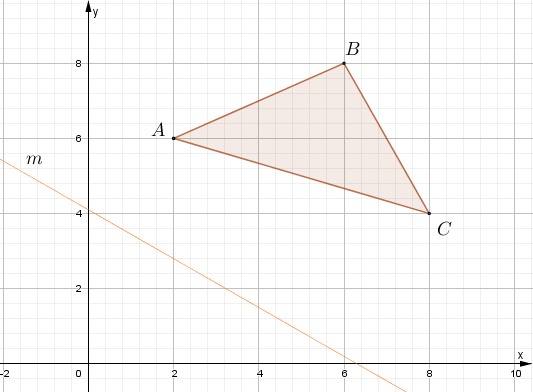
Paso # 1. Trazar rectas perpendiculares segmentadas desde el eje de simetría hacia cada vértice. Para el trazo perpendicular utiliza una regla y un cartabón o escuadra.
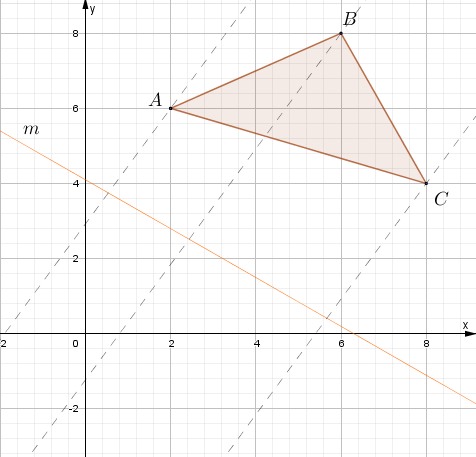
Paso # 2. Utiliza una regla para medir la distancia entre cada vértice y el eje de reflexión.
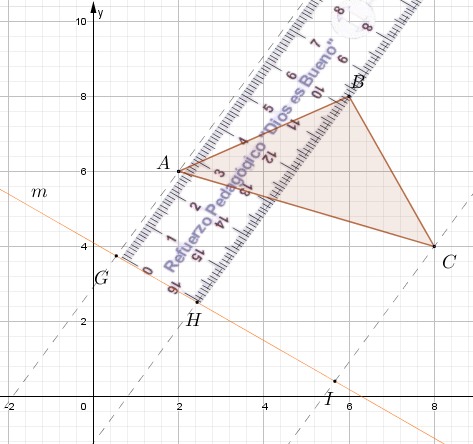
Paso # 3. Ubicar los vértices imágenes al otro lado del eje de reflexión.
¡A jugar con las transformaciones geométricas: traslaciones, rotaciones y reflexiones!
Llegó el momento de poner en practica lo que ya conoces hasta ahora.
Selecciona el tipo de transformación y observa como se ven las imágenes.
¿Te ha gustado esta simulación? ¡Nos encantaría saber tu opinión! Cuéntanos en los comentarios qué te ha parecido, si te ha sido útil o si tienes alguna duda o sugerencia, inmediatamente te contestaremos. Tu participación nos ayuda a seguir creando contenido que inspire y enseñe. ¡Te leemos!
Homotecia
| Se trata de un proceso que genera una imagen de distinto tamaño pero su forma la mantiene. Es conocida también con el nombre dilatación y se construye a partir de un centro fijo (centro de homotecia) y un factor de escala (razón). |
Características
La homotecia presenta varias características importantes, entre las que se destacan:
- Posee un centro llamado centro de homotecia. Es el punto donde se proyectan y se trazan segmentos hasta los vértices de la imagen.
- Un factor de escala k. Llamada también razón de homotecia, determina si la imagen es ampliada o reducida y además indica la orientación de la misma.
- Si el factor de escala es:
k > 1, la imagen es ampliada alejándose del punto homotecia.
0 < k < 1, la imagen es reducida acercándose al punto homotecia
k < 0, la imagen es invertida respecto al centro cambiando su orientación. Esta puede quedar reducida, ampliada o quedar al mismo tamaño.
k = 0, Todos los puntos de la imagen queda ubicada en el centro de homotecia. Es decir, no se genera una imagen visible.
k = 1, La imagen coincide con la figura dada. - Cambia el tamaño de la imagen pero no su forma, generando imágenes semejantes.
- Las longitudes de la figura es proporcional con las longitudes de la imagen.
Observa la siguiente tabla, allí apreciarás los distintos factores de escala.
k > 1 | 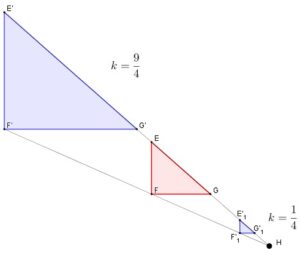 |
0 < k < 1 | |
k < 0 | 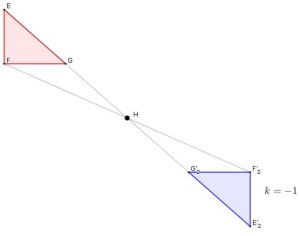 |
k = 0 | 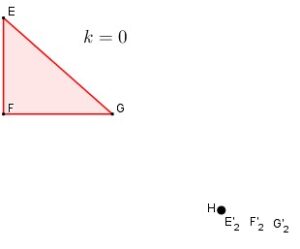 |
k = 1 | 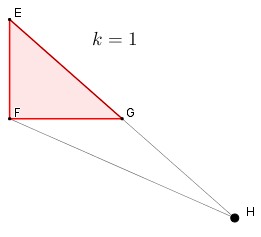 |
¿Cómo debes realizar una homotecia?
A continuación, te mostraré, mediante un ejemplo, cómo aplicar una homotecia a un polígono paso a paso. Verás cómo identificar el centro de homotecia y cómo aplicar el factor de escala, de esta forma obtendrás la figura transformada con exactitud.
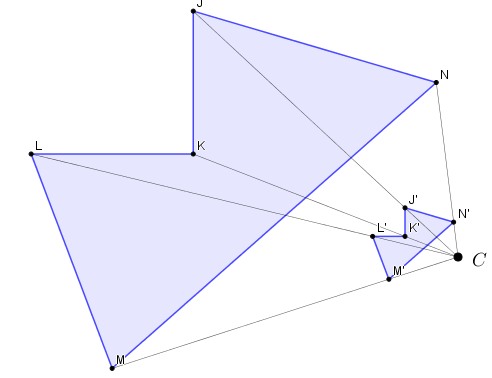
Ejemplo. Obtener la imagen de un polígono por homotecia
El centro es el punto C con un factor de escala 1/5.
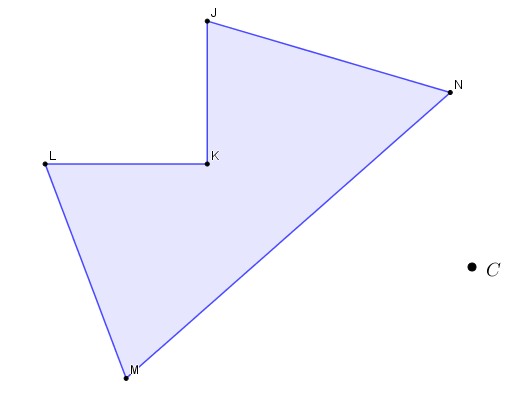
Para realizar la homotecia debes llevar a cabo los siguientes pasos:
I. Dibuja segmentos desde cada vértice del polígono hasta el punto C.
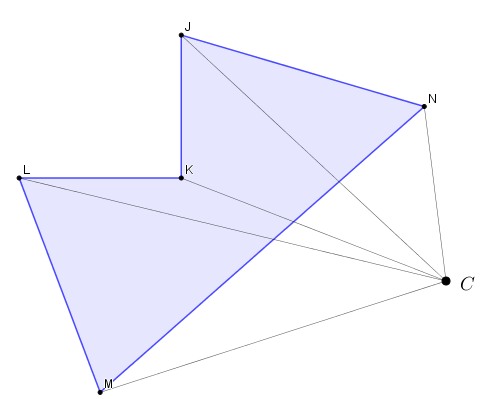
II. Mide cada longitud y lo multiplicas por el factor de escala 1/5, para obtener las longitudes desde el punto centro “C” a cada vértice imagen.
| Longitud del centro a la figura | Multiplicación con el factor de escala 1/5 = 0.2 | Longitud del centro a la imagen |
| $$\overline{CM}=9.09cm$$ | $$9.09cm\cdot 0.2cm=$$ | $$1.82cm$$ |
| $$\overline{CL}=10.92cm$$ | $$10.92cm\cdot 0.2cm=$$ | $$2.18cm$$ |
| $$\overline{CK}=7.14cm$$ | $$7.14cm\cdot 0.2cm=$$ | $$1.43cm$$ |
| $$\overline{CJ}=9.49cm$$ | $$9.49cm\cdot 0.2cm=$$ | $$1.90cm$$ |
| $$\overline{CN}=4.91cm$$ | $$4.91cm\cdot 0.2cm=$$ | $$0.98cm$$ |
III. Marcar los vértices imagen.
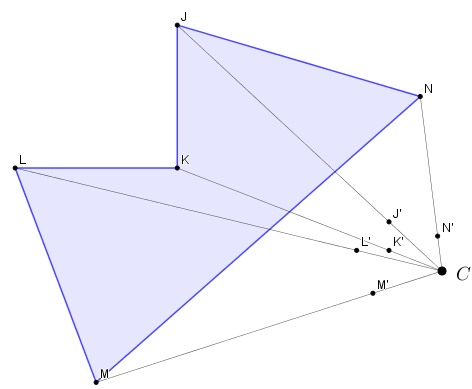
IV. Unir los vértices para obtener el polígono M´L´K´J´N´ imagen por homotecia del polígono dado.
¡A jugar con la Homotecia!
Pon en practica todo lo que ya conoces y diviértete jugando con la homotecia.
En el botón rojo seleccionas el factor de escala, en caso que la imagen no se vea, no te preocupes debes arrastrar o mover el área de la simulación para encontrarla.
Si tienes preguntas o quieres contarnos tu experiencia, te invitamos a dejar tus comentarios al final de este post. Tu participación nos ayuda a crear contenido que inspire y enseñe.
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
I. Diga ¿Cuánto es h y k?

II. ¿Cuánto es el ángulo de rotación de esta transformación?

III. Dibuja la imagen de la siguiente figura, donde la recta m es el eje de reflexión.
IV. Los vértices de un rombo son: A(10,4); B(12,7); C(14,4); y D(12,1). Si los vértices imágenes por la traslación es: A´(11,5); B´(13,8); C´(15,5); y D´(13,2). ¿Cuánto se trasladó verticalmente y horizontalmente?.
V. Le aplican una rotación al punto F(-2,1) con centro en el origen R y un ángulo “x”. La imagen del punto es F´(-6,5).¿Cuál es el valor del ángulo x?
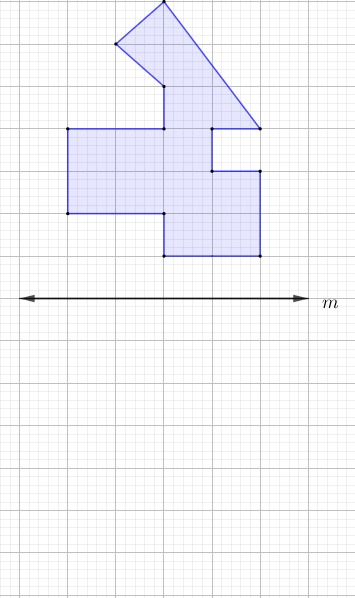
VI. Traslada la figura a continuación h = 5 y k = 0
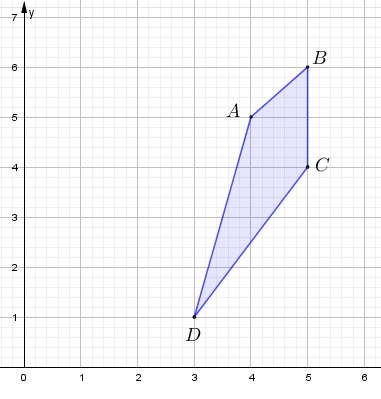
VII. Rota a 60° horario con centro en O, el siguiente cuadrilátero.

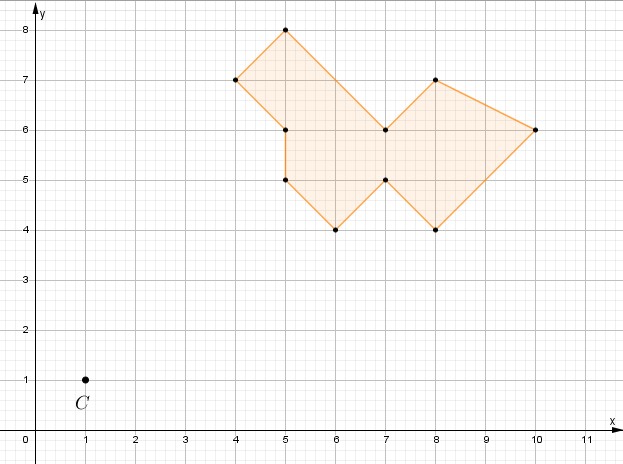
VIII Identifica el centro y el factor de homotecia en ambas imágenes.

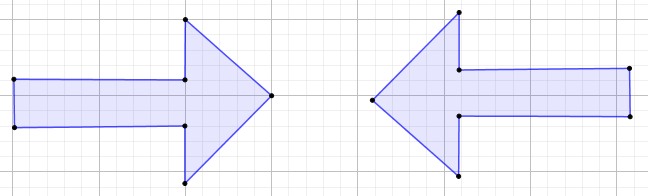
IX. Representa la homotecia con un factor de homotecia = 2
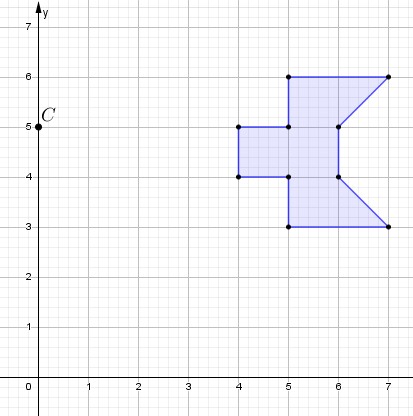
X. Construye la homotecia con dos factores de escala: ½ y 1/5 de la siguiente figura.
¡Ayúdanos a mejorar!
¿Qué te pareció esta guía de transformaciones geométricas? ¿Conoces algún otro tipo de transformación que debería añadir? ¡Deja tus ideas y preguntas en los comentarios! Tu opinión nos ayudará a crear contenido aún más útil.