¿Quieres aprender Fracciones Equivalentes, a Simplificar, Amplificar, y hacerlo todo con Simulación? ¡Entonces has llegado al lugar correcto!
¿Sabías que esta habilidad te permite repartir una pizza entre tus amigos de distintas formas sin que nadie coma menos? Alguna vez has repartido una pizza y notaste que algunas porciones eran iguales aunque parecieran diferentes? O quizá, mientras jugabas, viste que tu nivel de energía mostraba «2/4» y luego «1/2», pero tu personaje seguía teniendo la misma fuerza. ¡Eso no es magia, son partes que representan la misma cantidad!
En este post, aprenderás a identificarlas, cómo amplificarlas o simplificarlas, y descubrirás qué significa que una fracción sea irreducible. Además, contarás con dos simuladores donde podrás jugar y fortalecer tus conocimientos. ¡Prepárate para dominar las Fracciones Equivalentes!
¿Qué significado tiene el denominador?
Indica el número de partes en que divide el todo. El denominador es ubicado en la parte de abajo de la fracción. Observa la imagen, el círculo representa el todo y las 3 partes divididas es el denominador.
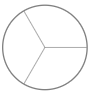
¿Qué función cumple el numerador?
Muestra el número de partes que se toman. La zona sombreada de verde simboliza las partes tomadas, es decir, el numerador.
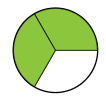
Por lo tanto la fracción se escribe: $$\frac{2}{3}$$
¿Qué son las fracciones equivalentes?
Son fracciones que poseen denominadores y numeradores diferentes, pero representan la misma proporción de un todo.
Presta atención al siguiente ejemplo:
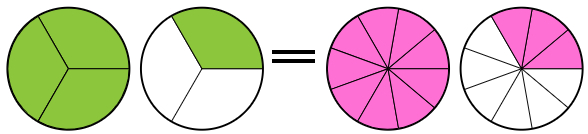
Los círculos sombreados en verde representan: $$\frac{4}{3}$$
Los círculos sombreados de fucsia expresa: $$\frac{12}{9}$$
Conclusión: Los círculos (sombreados de verde) de la izquierda tienen menos partes dividida y los círculos (sombreados de fucsia) de la derecha posee mayores porciones, pero sus zonas sombreadas son las mismas. Se concluyen que son fracciones equivalentes ya que gráficamente representan las mismas áreas.
$$\frac{4}{3}=\frac{12}{9}$$
¿Cómo identificar fracciones equivalentes?
Para identificar si las fracciones son equivalentes debes aplicar un procedimiento denominado producto cruzado.
El producto cruzado consiste en multiplicar el numerador de una de las fracciones por el denominador de la otra fracción, si se obtiene el mismo resultado es que ambas fracciones son equivalentes.
Observa la imagen allí se muestra el producto cruzado, si ambos productos son iguales la fracción es equivalente.
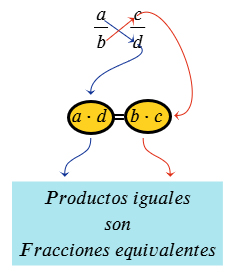
Ejemplo # 1: Verifique si las fracciones a continuación son equivalentes.
$$\frac{4}{3} y \frac{12}{9}$$
Se aplica el producto cruzado:
$$4.9=3.12$$
$$36=36$$
Conclusión: Queda demostrado que ambas fracciones son equivalentes.
Ejemplo # 2: Verifique si ambas fracciones son equivalentes.
$$\frac{4}{5} y \frac{7}{8}$$
Producto cruzado:
$$4.8=7.5$$
$$32≠35$$
Conclusión: No son equivalentes.
Amplificación de fracciones
Es multiplicar cada término (numerador y denominador) de la fracción por un mismo número entero diferente a cero para obtener una fracción equivalente con mayores partes.
Aunque la fracción resultante es de mayor número de partes, el valor que representa sigue siendo el mismo.
Observa se va a amplificar la fracción 3/5 por el triple. El número entero multiplica con el numerador y el denominador.
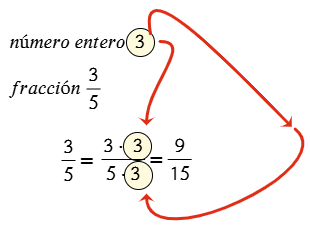
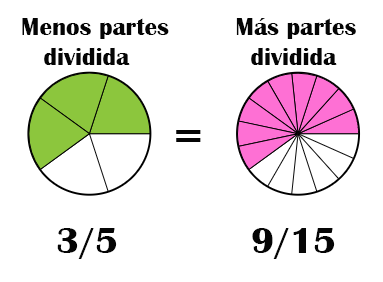
Respuesta: La fracción equivalente de 3/5 = 9/15 con muchas más partes pero es una misma área, mira la imagen:
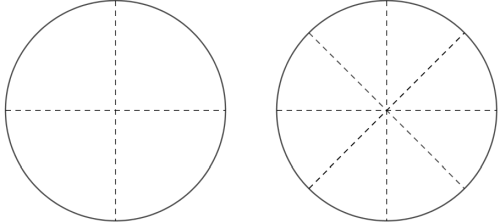
Ejemplo # 1: Luisa pide una pizza y se la entregaron cortada en 4 porciones, ella al ver esto le solicita al pizzero que la corte en 8 porciones ya que son para 8 personas.
Análisis: Como se requiere otra fracción con partes más pequeñas se aplica una amplificación por el doble, de esta manera garantiza 8 partes iguales para cada persona.
$$\frac{1}{4}=\frac{1.2}{4.2}=\frac{2}{8}$$
Ejemplo # 2: Amplifique las siguientes fracciones por 5.
a) 
b) 
¡Construye Fracciones Equivalentes como un experto! Experimenta la equivalencia con esta simulación.
Muchos videojuegos usan porcentajes (que son fracciones con denominador 100) por ejemplo si un objeto +25% de daño, en fracción es 25/100 de daño adicional, que es equivalente a ¼. Aunque tengan números diferentes representan lo mismo.
Con esta iniciativa interactiva sobre fracciones equivalentes, simplificar, amplificar con simulación, no solo entenderás la teoría, sino que podrás verlo y manipularlo con tus propias manos (o con tu ratón).
Esta herramienta te permitirá construir, simplificar y amplificar fracciones de manera visual. ¡Prepárate para dominar el arte de la equivalencia y que las fracciones ya no te den dolor de cabeza!
Si te gustó la simulación o tienes alguna sugerencia, déjanos tu comentario al final de este post. Tu opinión nos ayuda a mejorar cada día y a ofrecerte un contenido de mayor calidad.
Simplificación de fracciones
Es dividir cada término (numerador y denominador) de la fracción entre un divisor común obteniendo una fracción equivalente con menos partes.
Ejemplo: Simplifica la fracción 28/42.
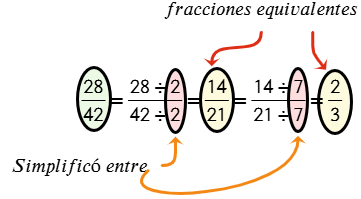
Respuesta: Las fracciones equivalentes de 28/42 es:
$$\frac{28}{42}=\frac{14}{21}=\frac{2}{3}$$
Posee menos partes pero representan lo mismo.
Fracción irreducible
Una fracción es irreducible cuando no permite ser simplificada, es decir, cuando sus términos (numerador y denominador) son primos entre sí, O sea, el máximo común divisor (M.C.D.) de sus términos es uno.
Para llevarlo a cabo debes aplicar el Máximo Común Divisor (M.C.D.) a ambos términos.
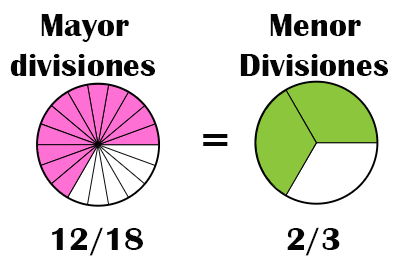
Ejemplo: Simplifica la fracción 12/18 hasta obtener una fracción irreducible.
El M.C.D. (12,18) es 6
$$\frac{12}{18}=\frac{12÷6}{18÷6}=\frac{2}{3}$$
Respuesta: La fracción equivalente 2/3 es irreducible.
¡A jugar! con fracciones equivalentes simplificar amplificar con simulación pon a prueba tus habilidades y Gana la partida
¿Crees que ya eres un crack en fracciones equivalentes? ¡Es hora de demostrarlo! Con nuestro juego fracciones equivalentes simplificar, amplificar con simulación, no solo vas a practicar, ¡sino que te vas a divertir a lo grande!
Supera niveles, acumula puntos y compite para ver quién es el más rápido en identificar las fracciones que valen lo mismo. Este desafío pondrá a prueba tu mente y te convertirá en un verdadero maestro de las fracciones equivalentes. ¡Olvídate de las clases aburridas y prepárate para un reto que te hará dominar la simplificación y amplificación!
¿Aceptas el desafío?
¿Qué te pareció este simulador de fracciones equivalentes? Tu opinión es muy importante para nosotros. Si te gustó o tienes alguna idea para mejorarlo, ¡escríbela en los comentarios! Al final de este post.
Estamos comprometidos con crear experiencias divertidas y educativas para que aprender sea cada vez más emocionante.
Actividades: Fracciones equivalentes, simplificar, amplificar con simulación
1.Determina qué par de fracciones son equivalentes.
| a) | ½ y 2/3 | c) | 5/12 y 25/60 |
| b) | 7/3 y 14/6 | d) | -3/2 y -6/4 |
2.Halla tres fracciones equivalentes a cada una de las fracciones dadas.
| a) | 1/5 | d) | 4/15 |
| b) | 2/3 | e) | 21/9 |
| c) | 3/9 | F) | 4/9 |
3.Simplifica las siguientes fracciones hasta obtener una fracción irreducible.
| a) | 4/6 | f) | 8/8 |
| b) | 144/4 | g) | 234/270 |
| c) | 15/33 | h) | 17/102 |
| d) | 50/70 | i) | 23/46 |
| e) | 12/512 | j) | 1032/864 |
4.Analiza y responde.
a)¿Cuál es el numerador de una fracción que es equivalente a 41/45 y su denominador es 90.
b)¿Cuál es el denominador de una fracción que es equivalente a 54/42 y su numerador es 18?
- Grafica cada fracción con su fracción irreducible.
a) 4/8
b) 12/20
6.Analiza y responde.
Valeria y Samuel están editando un video para subirlo a sus redes sociales. Valeria dice que ya ha editado 2/4 del video, mientras que Samuel asegura haber editado 1/2. ¿Quién ha editado más parte del video?
Comparte esto:
Descubre más desde LaProfematematiK "Dios es Bueno"
Suscríbete y recibe las últimas entradas en tu correo electrónico.