¿Estás buscando problemas resueltos de problemas resueltos de ángulos de Elevación y Depresión (paso a paso)? ¿Alguna vez te has preguntado cómo se calcula la altura de una montaña o la distancia a la que se encuentra un barco en el mar? La respuesta se encuentra en la trigonometría, específicamente en los conceptos de ángulo de elevación y depresión. Estos ángulos son esenciales en nuestra vida diaria, desde la construcción de edificios hasta la navegación. Por ejemplo, un topógrafo usa el ángulo de elevación para medir la altura de un rascacielos sin escalarlo, y un guardacostas en un faro utiliza el ángulo de depresión para determinar la distancia de un buque.
Para dominar este tema, es importante entender la teoría primero. Por eso, te invito a leer la parte teórica y luego poner a prueba tus conocimientos con los 20 problemas desarrollados paso a paso. Así, estarás preparado para resolver cualquier desafío que se te presente.
Ángulos de elevación y depresión?
Los ángulos de elevación y depresión surgen cuando un observador mira un objeto que no está al mismo nivel que él. Para definirlos, se utiliza una línea horizontal imaginaria que parte de los ojos del observador. En ambas situaciones se origina un triángulo rectángulo, lo que permite aplicar las razones trigonométricas para solucionar problemas de altura y distancia.
¿Qué es el ángulo de elevación?
Cuando el observador mira un objeto que está por encima de su línea horizontal de visión, el ángulo que se forma entre la línea de visión y esa horizontal se llama ángulo de elevación.
¿Qué es el ángulo de depresión?
Por el contrario, cuando el observador mira un objeto que está por debajo de su línea horizontal, el ángulo que se forma entre la línea de visión y la horizontal se conoce como ángulo de depresión.
Recomendaciones para solucionar problemas
Para solucionar distintas situaciones es necesario llevar a cabo una serie de pasos ordenados. Estos pasos son los siguientes:
1. Dibujar un diagrama para cada problema
Utiliza el triángulo rectángulo el cual es formado con la línea imaginaria horizontal. En esta figura especifica la altura del objeto (cateto opuesto), distancia del objeto (cateto adyacente), distancia del observador al objeto (hipotenusa) y el ángulo de elevación o depresión.
2. Identificar el tipo de ángulo
Si se mira hacia arriba es un ángulo de elevación y si es lo contrario es un ángulo de depresión. Existen casos donde el ángulo de elevación desde un punto es igual al ángulo de depresión desde otro punto, esto se debe a que son ángulos alternos internos entre líneas paralelas (la horizontal de cada observador).
3. Usar razones trigonométricas
Según el tipo de problema debes elegir la razón trigonométrica que relacione los datos dados y la incógnita que requieres determinar.
4. Identificar el tipo de altura
Identificar correctamente cada tipo de altura es fundamental para resolver los problemas con precisión.
Altura del observador: La línea de visión horizontal siempre se traza desde la altura de los ojos de la persona que observa.
Altura calculada: Es la parte de la altura que se obtiene al usar las razones trigonométricas. Esta mide la distancia vertical desde la línea de visión del observador hasta la punta del objeto.
Altura total: Para hallar la altura completa de un objeto, se debe sumar la altura calculada con la altura del observador.
Guía de 20 problemas resueltos
Esta guía de 20 problemas desarrollados paso a paso está diseñada para que apliques todo lo que has aprendido. Cada ejercicio te desafiará a usar los conceptos de elevación y depresión en diferentes escenarios, asegurando que adquieras la confianza necesaria para resolver cualquier problema de este tipo por tu cuenta.
Problema # 1
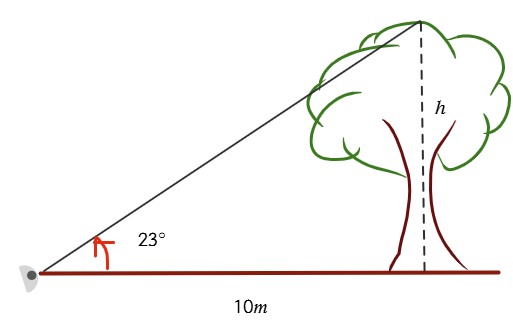
A una distancia de 10 m de la base de un árbol, la punta de éste se observa bajo un ángulo de 23°. Calcula la altura del árbol.
Solución
1. Dibujar la situación.
2. Tipo de ángulo: elevación.
| Datos | Operación |
| d=10m α=23° h=? | $$tan\alpha =\frac{h}{10m}\Rightarrow $$ $$h=10m\cdot tan23^{\circ }=4,2m$$ $$h=4,2m$$ |
Problema # 2
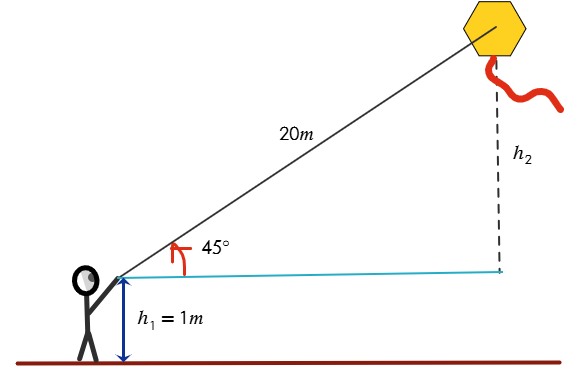
Un niño tiene una cometa, el cual hace volar sosteniendo una cuerda a un metro del suelo. La cuerda se tensa formando un ángulo de 45° con respecto a la horizontal. Obtén la altura de la cometa con respecto al suelo si el niño suelta 20 metros de cuerda.
Solución:
1. Dibujar la situación.
2. Tipo de ángulo: elevación.
| Datos | Operación |
| h2=? α=45° c=20m h1=1m | $$sen45^{\circ }=\frac{h_{2}}{20m}\Rightarrow $$ $$h_{2}=20m\cdot sen45^{\circ }=$$ $$h_{2}=\frac{20m\cdot \sqrt{2}}{2}=$$ $$h_{2}=10\sqrt{2}m$$ $$h_{t}=h_{1}+h_{2}$$ $$h_{t}=1m+10\sqrt{2}m\approx 15,1m$$ |
Problema # 3
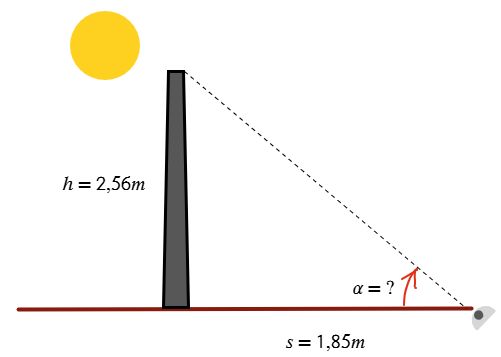
Determine el ángulo de elevación del Sol si un poste de 2.56 m proyecta una sombra de 1.85 m. La respuesta en grados, min, y segundo.
Solución:
1. Dibujar la situación.
2. Tipo de ángulo: elevación.
| Datos | Operación |
| h=2,56m α=? s=1,85m | $$tan\alpha =\frac{2,56m}{1,85m}\Rightarrow $$ $$\alpha =tan^{-1} 1,\overline{38}$$ $$\alpha \approx 54,146^{\circ }$$ $$58^{\circ}\ 8^{\prime}\ 46^{\prime\prime}$$ |
Problema # 4
Un globo de aire caliente sube con un ángulo de elevación con respecto a un punto A de 46°10’. Calcula la altura a la que se encuentra el globo, con respecto a un punto P del Suelo, si la distancia de éste al punto A es de 50 m.
Solución:
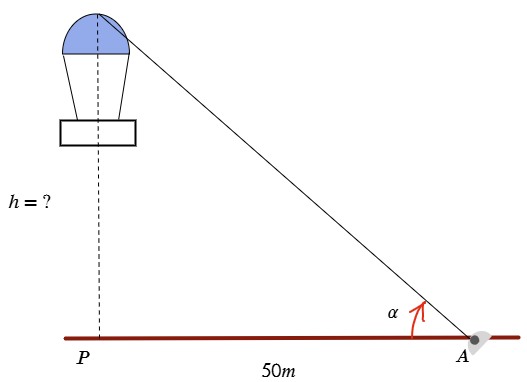
| Datos | Operación |
| α=46°10´ h=? dPA=50m | $$tan46^{\circ}\,10’\,=\frac{h}{50m}\Rightarrow $$ $$h=50\cdot tan46^{\circ}\,10’\,=$$ $$h=50m\cdot 1,04158=$$ $$h=52,078m$$ |
Problema # 5
Desde lo alto de una torre cuya altura es de 25 m, se observa un automóvil alejándose de la torre, con un ángulo de depresión de 32°, si un instante después el ángulo es de 26°. ¿Qué distancia se ha desplazado el automóvil?
Solución:
1. Dibujar la situación.
2. Tipo de ángulo: depresión.
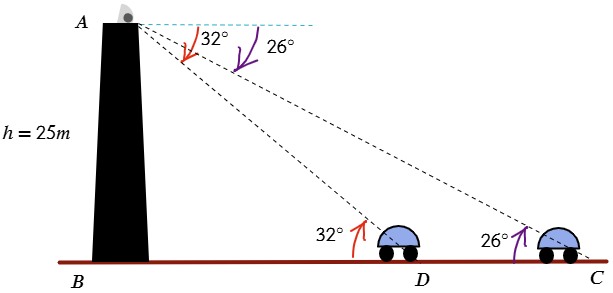
| Datos | Operación |
| h=25m α1 =32° α2 =26° d=? | Para resolver este problema se aplica ángulos alternos internos. $$tan32^{\circ }=\frac{25m}{\overline{BD}}\Rightarrow $$ $$\overline{BD}=40m$$ $$tan26^{\circ }=\frac{25m}{\overline{BC}}\Rightarrow $$ $$\overline{BC}\approx 51,3m$$ $$\overline{BC}=\overline{BD}+\overline{DC}\Rightarrow $$ $$\overline{DC}=\overline{BC}-\overline{BD}$$ $$\overline{DC}=51,3m-40m$$ $$\overline{DC}=11,3m$$ |
Problema # 6
Galileo quería soltar una bola de madera y una bola de hierro desde una altura de 100 m y medir el tiempo que tardan en caer. Encontró una rampa con una inclinación de 12°por la que podía subir para llegar a una altura de 100 m. ¿Cuánto tendría que caminar Galileo sobre la rampa?
Solución:
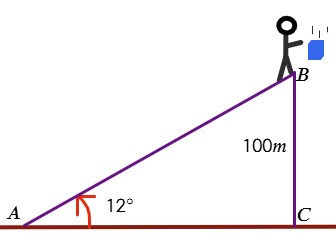
| Datos | Operación |
| h=100m α=12° $$\overline{AB}=?$$ | $$sen12^{\circ }=\frac{100m}{\overline{AB}}\Rightarrow $$ $$\overline{AB}=\frac{100}{sen12^{\circ }}$$ $$\overline{AB}\approx 480,97m$$ |
Problema # 7
Bob construye una cabaña de madera. La cabaña mide 30 m. Bob obtuvo varias vigas de la madera 17 m largo para el techo de la caballa. Naturalmente, quiere poner las vigas a un ángulo tal que cada par de vigas opuestas se encuentren exactamente en el medio. ¿Cuál es el ángulo de elevación de las vigas del techo en grados?
Solución:
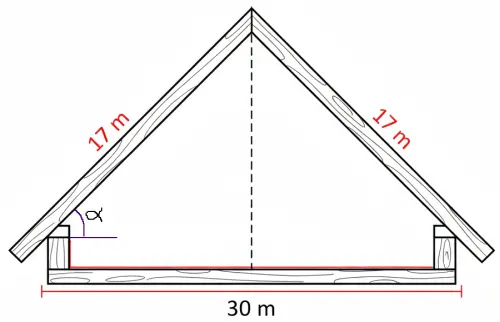
| Datos | Operación |
| bcabaña=30m lviga=17m α=? | $$cos\alpha =\frac{15}{17}\Rightarrow $$ $$\alpha =cos^{-1}\frac{15}{17}$$ $$\alpha \approx 28,1^{\circ }$$ |
Problema # 8
Howard diseña un juego mecánico de sillas voladoras. Los cables de la sillas son de 4 m de largo, y a si máxima velocidad se inclinan a un ángulo de 23°. Howard quiere que las sillas estén a 3,5 m del piso cuando el juego va a velocidad máxima. ¿Qué tan alto debe ser el poste del juego mecánico? Redondea tu respuesta final a la centésima más cercana.
Solución:
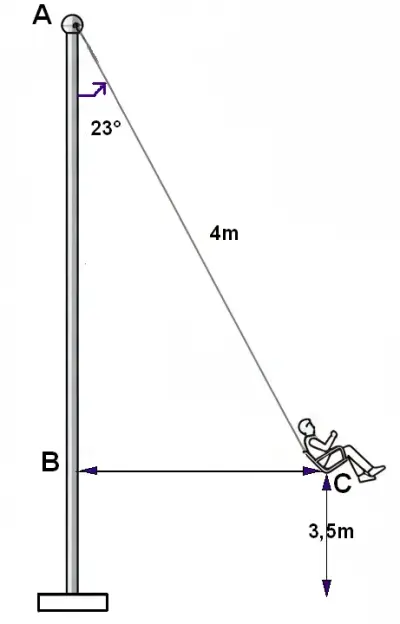
| Datos | Operación |
| lcable=4m α=23° hpiso=3,5m hposte=? | $$cos23^{\circ } =\frac{\overline{AB}}{4m}\Rightarrow $$ $$\overline{AB}=4m\cdot cos23^{\circ }$$ $$\overline{AB}\approx 3,68m$$ $$h_{poste}=3,68m+3,5m$$ $$h_{poste}=7,18m$$ |
Problema # 9
Los amigos de Stella le regalaron una clase de paracaidismo para su cumpleaños. Su helicóptero despegó del centro de paracaidismo ascendiendo en un ángulo de 37° y recorrió 2.1 km antes de que ella saltará en dirección perpendicular al suelo. ¿A qué distancia está del centro de paracaidismo aterrizó Stella?
Solución:
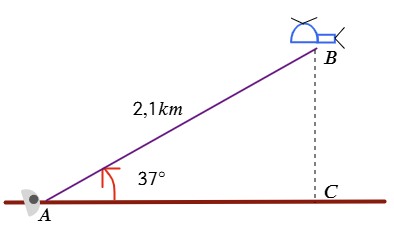
| Datos | Operación |
| α=37° d=2,1km h=? | $$cos37^{\circ }=\frac{\overline{AC}}{2,1m}\Rightarrow $$ $$\overline{AC}=2,1m\cdot cos37^{\circ } $$ $$\overline{AC}\approx 1,68m $$ |
Problema # 10
El conejo bugs estaba a 42 m bajo tierra, y excavaba hacia Albuquerque, cuando quiso salir a la superficie. Cambió su dirección y excavó 100 m en diagonal a través del suelo hasta salir a la superficie. ¿Cuál es el ángulo de elevación, en grados, del ascenso de Bugs?
Solución:
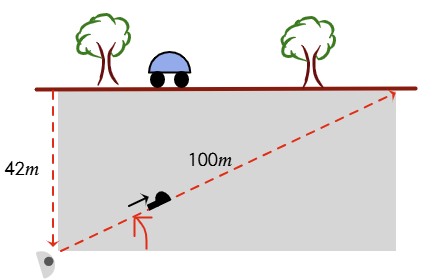
| Datos | Operación |
| P=42m d=100m α=? | $$sen\alpha =\frac{42m}{100m}\Rightarrow $$ $$\alpha =arcsen0,42$$ $$\alpha \approx 24,8^{\circ }$$ |
Problema # 11
Pablo vio un árbol al otro lado del río y marcó el punto que estaba directamente frente a él. Después caminó hasta otro punto que estaba 15 metros río abajo y encontró que el ángulo formado por su lado del río y la línea que lo conectaba con el árbol era 76°.¿Cuál es el ancho el río? Redondear a la centésima más cercana.
Solución:
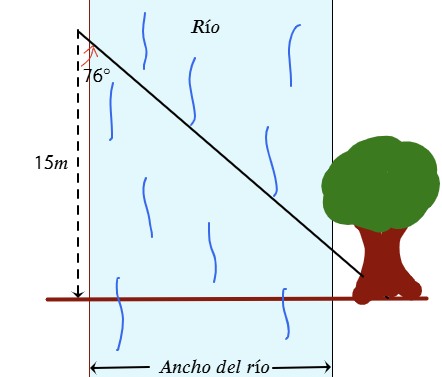
| Datos | Operación |
| d=15m α=76° anchorío=? | La situación forma un triángulo rectángulo y en función a los datos conocidos conviene aplicar la tangente. $$tan14^{\circ }=\frac{15m}{ancho_{rio}}\Rightarrow $$ $$ancho_{rio}=\frac{15m}{tan14°} $$ $$ancho_{rio}\approx 60,16m$$ |
Problema # 12
Un extraterrestre diminuto pero horrible está parado en la punta de la Torre Eiffel (que mide 324 metros de alto) y ¡amenaza con destruir la ciudad de Paris! Un agente de los Hombres de Negro está parado a nivel del piso, a 54 metros de distancia a la torre, y apunta su pistola láser al extraterrestre. A qué ángulo, en grados, ¿debe el agente disparar su pistola láser? Redondear a la décima más cercana.
Solución:
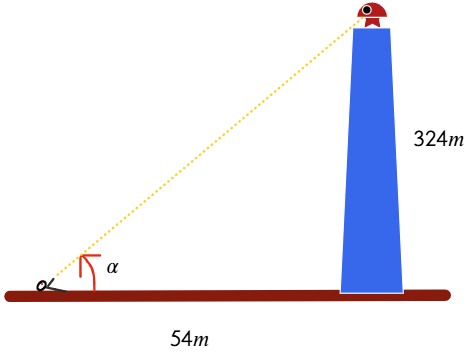
| Datos | Operación |
| h1=324m d=54m α=? | $$tan\alpha =\frac{324m}{54m}\Rightarrow $$ $$\alpha =arctan\frac{324}{54} $$ $$\alpha \approx 80,5^{\circ }$$ |
Problema # 13
Isabella hace una bandera enorme de su país, la República de las Seychelles, sobre un lienzo de 20 por 10 metros. Para ello, tiene que dibujar una línea diagonal desde la esquina inferior izquierda hasta el borde derecho, a 7 metros de altura. Como la línea diagonal es demasiado grande para utilizar una regla, Isabella quiere encontrar el ángulo de la diagonal y dibujarlo usando un transportador. ¿Cuál es el ángulo de elevación de la diagonal en grados? Redondea tu respuesta final a la décima más cercana.
Solución:
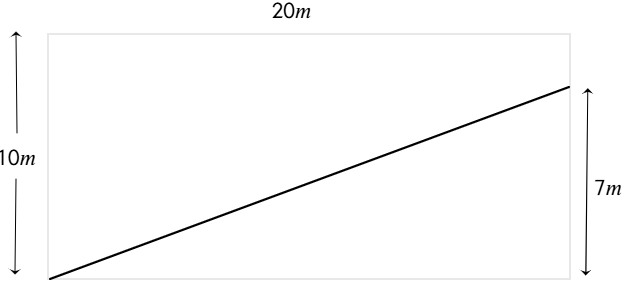
| Datos | Operación |
| a=20m l=10m d=7m α=? | $$\alpha =arctan\frac{7m}{20m}$$ $$\alpha \approx 19,3^{\circ }$$ |
Problema # 14
Arquímedes se fue a dormir junto a una gran roca. Quería levantarse a las 7 a.m., pero ¡los despertadores aún no se habían inventado! Por ello decidió dormir en un sitio en el cual la sombra de la roca terminara cuando fueran las 7 a.m. y así despertar con la luz directa del sol. Arquímedes sabía que a las 7 a.m. la luz del sol toca el suelo en un ángulo de 31°. La roca junto a la cual durmió mide 5 metros de altura. ¿Qué tan lejos de la roca durmió Arquímedes? Redondea tu respuesta final a la centésima más cercana.
Solución:
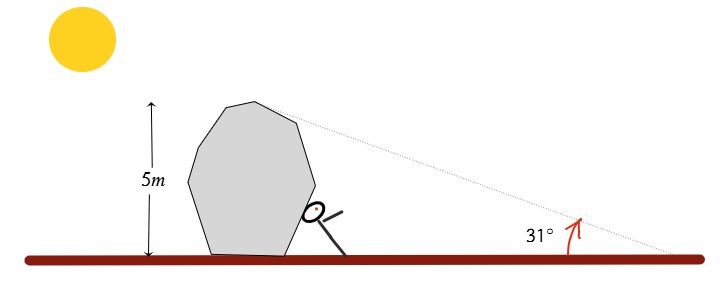
| Datos | Operación |
| α=31° h=5m d=? | $$tan31^{\circ } =\frac{15}{d}\Rightarrow $$ $$ d=\frac{15}{tan31^{\circ }}$$ $$ d\approx 8,32m$$ |
Problema # 15
Una persona cuyos ojos están a 1.3m del suelo, observa una pintura que se encuentra a un metro del suelo y mide 1.60 m. Dicha persona se encuentra a 3 metros de distancia de la pintura. ¿Cuál es el ángulo completo de la pintura valorada por B/.500.00?
Solución:
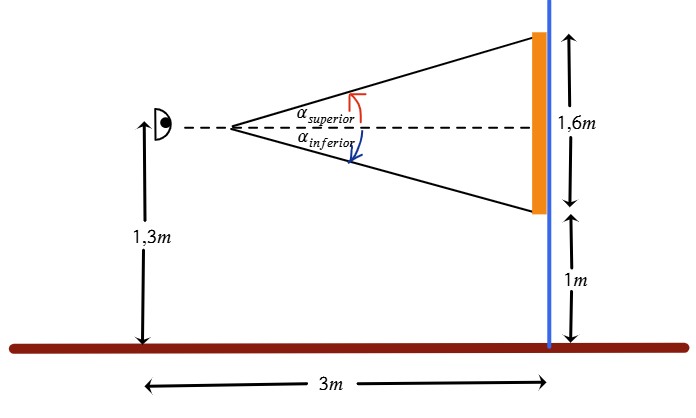
| Datos | Operación |
| h1=1,3m h2=1m hpersona=1,6m d=3m αc=? Valor=$1500 | $$h_{1}=1,3m-1m=0,3m$$ $$\alpha _{inferior}=arctan\left ( \frac{0,3m}{3m} \right )$$ $$\alpha _{inferior}\approx 5,71^{\circ }$$ $$\alpha _{superior}=arctan\left ( \frac{1,3m}{3m} \right )$$ $$\alpha _{superior}\approx 23,43^{\circ }$$ $$\alpha _{c}=\alpha _{inferior}+\alpha _{superior}$$ $$\alpha _{c}=5,71^{\circ }+23,43^{\circ }$$ $$\alpha _{c}=29,14^{\circ }$$ |
Problema # 16
Un maleante es perseguido por un patrullero, quien es apoyado desde el aire por un helicóptero. Si el ángulo de depresión desde el helicóptero hasta donde se encuentra el delincuente es de 25° y el ángulo de depresión hasta el patrullero es de 65° y además una distancia entre el helicóptero y el patrullero es de 25 m. ¿Cuál es la distancia entre el helicóptero y el delincuente? ¿La distancia entre el patrullero y el delincuente? ¿La altura del helicóptero?.
Solución:
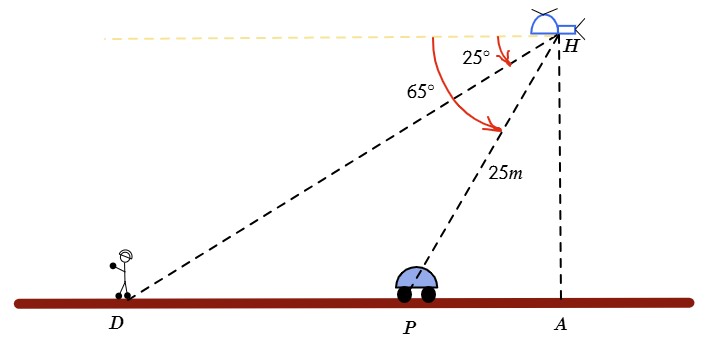
| Datos | Operación |
| $$\alpha=25^{\circ }$$ $$\overline{DH}=?$$ $$\overline{DP}=?$$ $$\overline{HA}=?$$ $$\overline{PH}=25m$$ | Para este problema se aplica ángulos alternos internos. Cálculo de la altura del helicóptero: $$sen65^{\circ }=\frac{\overline{HA}}{25m}\Rightarrow $$ $$\overline{HA}=25m\cdot sen65^{\circ }$$ $$\boxed{\overline{HA}\approx 22,66m}$$ Distancia entre el helicóptero y el delincuente: $$sen25^{\circ }=\frac{\overline{HA}}{\overline{DH}}\Rightarrow $$ $$\overline{DH}=\frac{\overline{HA}}{sen25^{\circ }}$$ $$\overline{DH}=\frac{22,66m}{sen25^{\circ }}$$ $$\boxed{\overline{DH}\approx 53,62m}$$ $$\underline{\hspace{3cm}}$$ $$\overline{DA}=\sqrt{\overline{DH}^{2}-\overline{HA}^{2}}$$ $$\overline{DA}=\sqrt{(53,62m)^{2}+(22,66m)^{2}}$$ $$\overline{DA}=48,60m$$ $$\overline{PA}=\sqrt{\overline{PH}^{2}-\overline{HA}^{2}}$$ $$\overline{PA}=\sqrt{(25m)^{2}-(22,66m)^{2}}$$ $$\overline{PA}=10,56m$$ $$\overline{DA}=\overline{DP}+\overline{PA}\Rightarrow $$ $$\overline{DP}=\overline{DA}-\overline{PA} $$ Distancia entre el patrullero y el delincuente: $$\overline{DP}=48,60m-10,56m $$ $$\boxed{\overline{DP}=38,04m} $$ |
Problema # 17
Un ingeniero civil desea conocer el ángulo elevación del topógrafo. Así como la distancia a la que se encuentra la asta bandera; se sabe que el asta mide la cuarta parte de la altura del edificio que es de 16 metros, y la distancia entre ambas es de 9metros (del asta hasta el edificio).
Solución:
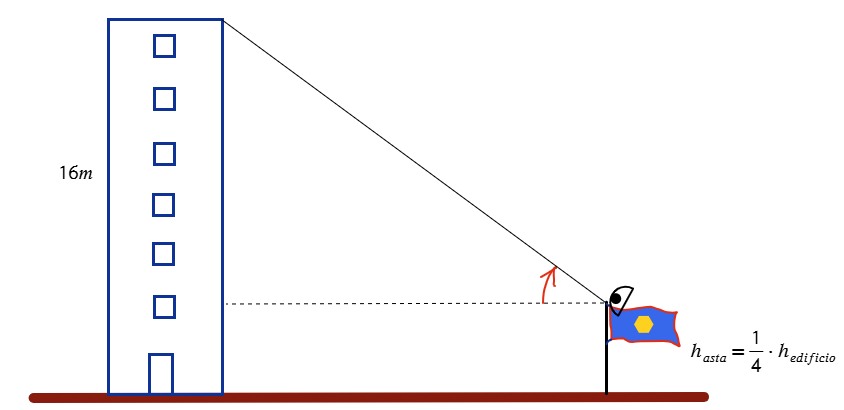
| Datos | Operación |
| α=? A=16/4=4m d edi-asta=9m | Cálculo de altura opuesta $$h_{opuesta}=h_{edificio}-h_{asta}$$ $$h_{opuesta}=16m-4m$$ $$h_{opuesta}=12m$$ $$\alpha =arctan\left ( \frac{12m}{9m} \right )$$ $$\alpha\approx 53,13^{\circ }$$ |
Problema # 18
Un cable está anclado a la cima de una torre de transmisión. El ángulo de elevación del anclaje del cable desde un punto en el suelo a 50 metros de la base de la torre es de 55°. Calcula la longitud del cable.
Solución:
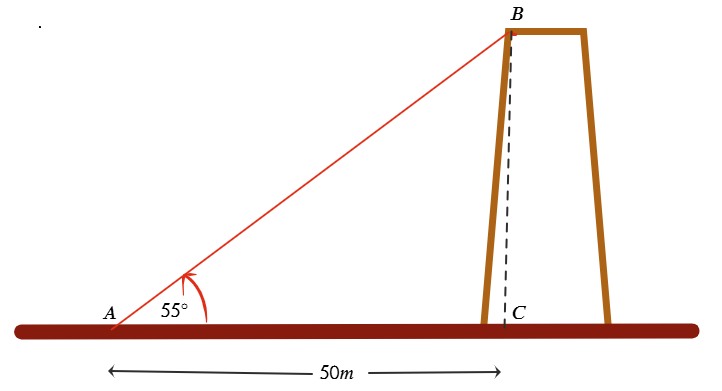
| Datos | Operación |
| d=50m α=55° lcable=? | $$cos55^{\circ }=\frac{50m}{\overline{AB}}\Rightarrow $$ $$\overline{AB}=\frac{50m}{cos55^{\circ }}$$ $$\overline{AB}\approx 87,17m $$ |
Problema # 19
Una escalera de 8 metros de largo se apoya contra una pared, formando un ángulo de 62° con el suelo. ¿A qué altura de la pared llega la escalera?
Solución:
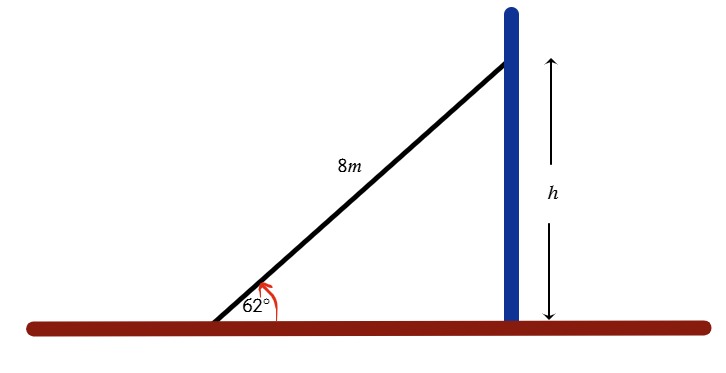
| Datos | Operación |
| l=8m α=62° h=? | $$sen62^{\circ }=\frac{h}{8m}\Rightarrow$$ $$h=8m\cdot sen62^{\circ }$$ $$h\approx 7,06m$$ |
Problema # 20
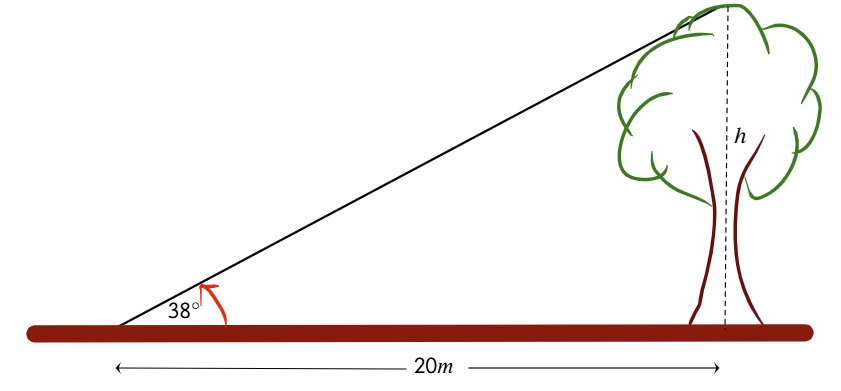
Un observador se encuentra a 20 metros de la base de un árbol. El ángulo de elevación a la cima del árbol es de 38°. Calcula la altura del árbol.
Solución:
| Datos | Operación |
| d=20m α=38° h=? | $$tan38^{\circ }=\frac{h}{20m}\Rightarrow$$ $$h=20m\cdot tan38^{\circ }$$ $$h\approx 15,63m$$ |
Pon a prueba tu visión matemática: ¡Ingresa al Quiz de Ángulos de Elevación y Depresión!
¿Listo para descubrir qué tan bien interpretas las situaciones del mundo real usando la trigonometría? Este quiz interactivo no es solo un juego: es una forma práctica, rápida y divertida de comprobar tu dominio sobre los ángulos de elevación y depresión, esos mismos que aparecen cuando observas un avión, miras desde un balcón o calculas la altura de un objeto sin tocarlo.
Cada pregunta está diseñada para retarte de una manera clara y visual, y al final podrás conocer tu puntuación y saber exactamente en qué nivel estás.
Haz clic ahora para iniciar el quiz y sigue explorando recursos, ejercicios y actividades que harán tus estudios mucho más fáciles y entretenidos. ¡No te quedes con la duda, acepta el reto y sorpréndete con tu resultado!
Queremos escucharte
Ahora que has visto cómo aplicar la trigonometría en distintos escenarios, te invito a que nos cuentes: ¿Qué problema de la vida diaria crees que podría resolverse utilizando los ángulos de elevación y depresión? ¡Déjanos tu idea en los comentarios!
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión