Valor numérico de las funciones trigonométricas

El valor numérico de las funciones trigonométricas es un tema fundamental en el estudio de la trigonometría, ya que permite evaluar funciones como el seno, coseno, tangente, cosecante, secante y cotangente cuando se les asigna un ángulo específico. Esta habilidad no solo es clave para resolver ejercicios trigonométricos, sino también para comprender y aplicar conceptos en áreas como la física, la geometría y situaciones de la vida cotidiana.

Dominar este tema te ayuda a desarrollar precisión en los cálculos, interpretar resultados correctamente y avanzar con mayor seguridad en contenidos mucho más complejos de la trigonometría.

¿Crees que dominas el valor numérico de las funciones trigonométricas?

Pon a prueba lo que sabes con una evaluación interactiva de 20 ejercicios y recibe retroalimentación inmediata.

👉 [Realizar evaluación ahora]

¿Qué es el valor numérico de una función trigonométrica?

El valor numérico de una función trigonométrica es el resultado que se obtiene al evaluar una función (seno, coseno, tangente, etc.).

Por ejemplo, al calcular sen30°, estas buscando el valor numérico del seno para ese ángulo específico. Este valor puede obtenerse a partir de una tabla de ángulos notables, calculadora o un procedimiento algebraico, dependiendo del caso.

Es importante diferenciar entre:

• La función trigonométrica, que representa una relación matemática.
• El valor numérico, que es el resultado concreto de evaluarla.

Funciones trigonométricas básicas

Las funciones trigonométricas básicas se definen a partir de un triángulo rectángulo y relacionan sus lados con uno de sus ángulos agudos.

Seno (sen)

El seno de un ángulo es la razón entre el cateto opuesto y la hipotenusa. $$sen\: \theta =\frac{cateto\: opuesto}{hipotenusa}$$

Coseno (cos)

El coseno de un ángulo es la razón entre el cateto opuesto y la hipotenusa. $$cos\: \theta =\frac{cateto\: adyacente}{hipotenusa}$$

Tangente (tan)

La tangente de un ángulo es la razón entre el cateto opuesto y el cateto adyacente. $$tan\: \theta =\frac{cateto\: opuesto}{cateto\: adyacente}$$

También puede expresarse como: $$tan\: \theta =\frac{sen\, \theta }{cos\, \theta }$$

Funciones trigonométricas recíprocas

Las funciones trigonométricas recíprocas se obtienen como el inverso de las funciones básicas. Estas permiten expresar relaciones adicionales dentro del triángulo rectángulo.

Cosecante (csc)

$$csc\: \theta =\frac{hipotenusa }{cateto\: opuesto }=\frac{1}{sen\, \theta }$$

Secante (csc)

$$sec\: \theta =\frac{hipotenusa }{cateto\: adyacente }=\frac{1}{cos\, \theta }$$

Cotangente (cot)

$$cot\: \theta =\frac{cateto\: adyacente }{cateto\: opuesto }=\frac{1}{tan\, \theta }$$

Ángulos notables y sus valores trigonométricos

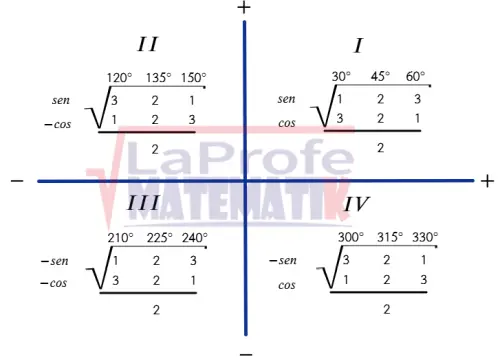
Los ángulos notables son aquellos cuyos valores trigonométricos se conocen exactamente y se utilizan con mucha frecuencia. Son tres ángulos en cada cuadrante, observa la imagen:

I: 30°, 45°, 60°.

II: 120°, 135°, 150°.

III: 210°, 225°, 240°.

IV: 300°, 315°, 330°.

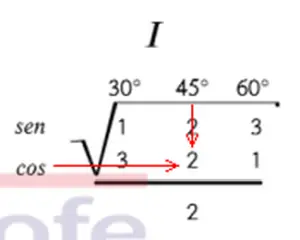
Procedimiento para calcular el valor numérico usando el plano cartesiano y  la raíz cuadrada (tabla de ángulos notables)

1. Identificar el cuadrante en el que se encuentra el ángulo. ( I, II, III y IV)
2. Si es seno o coseno te diriges horizontalmente y frenas cuando encuentres el número localizado verticalmente al ángulo.
   
3. Escribir la raíz cuadrada, con el número del paso anterior dividido entre dos.
4. Para calcular la tangente del ángulo, debes hallar el seno y el coseno y finalmente aplicar la relación: $$tan\: \theta =\frac{sen\, \theta }{cos\, \theta }$$
5. Determinar las recíprocas es muy fácil, sólo debes aplicar sus relaciones.

Conocer los valores del seno, coseno, tangente y sus recíprocos permite calcular rápidamente el valor numérico de muchas expresiones trigonométricas sin necesidad del uso de una calculadora.

El dominio de estos valores facilita la resolución de ejercicios, reduce errores y mejora la habilidad numérica del estudiante.

Cálculo del valor numérico paso a paso

Calcular el valor numérico de una función trigonométrica implica seguir un proceso ordenado y claro.

Sustitución directa de un ángulo

Cuando el ángulo es notable, se sustituye directamente en la función y se usa su valor conocido.

Ejemplo: $$\frac{sen\, 45^{\circ } }{cos\, 45^{\circ } }+\sqrt{2}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}+\sqrt{2}=1+\sqrt{2}$$

Valor numérico con operaciones combinadas

En muchos ejercicios, las funciones trigonométricas no aparecen de forma aislada, sino integradas en operaciones combinadas que incluyen sumas, restas, multiplicaciones, divisiones, fracciones, potencias y raíces cuadradas.

Para calcular correctamente el valor numérico, es fundamental seguir un orden lógico de trabajo:

1. Identificar los ángulos y sus cuadrantes, si es necesario.
2. Sustituir los valores trigonométricos utilizando la tabla de ángulos notables.
3. Conservar raíces y fracciones, evitando aproximaciones innecesarias.
4. Aplicar el orden de las operaciones: paréntesis → potencias y raíces → multiplicación y división → suma y resta.
5. Simplificar el resultado final.

Este tipo de ejercicios fortalece la precisión matemática y te prepara para evaluaciones de mayor nivel como por ejemplo demostraciones de identidades trigonométricas, ecuaciones trigonométricas, etc.

Observa los siguientes ejercicios resueltos paso a paso:

$$ sin 30^\circ + cos 60^\circ = \frac{1}{2} + \frac{1}{2} = 1 $$

$$ \frac{sin 45^\circ}{cos 45^\circ} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 $$

$$ 2sin 60^\circ – cos 30^\circ = 2\left(\frac{\sqrt{3}}{2}\right) – \frac{\sqrt{3}}{2} = \sqrt{3} – \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{2} $$

$$ \frac{sin 30^\circ + cos 60^\circ}{tan 45^\circ} = \frac{\frac{1}{2} + \frac{1}{2}}{1} = 1 $$

$$ sin^2 45^\circ + cos^2 45^\circ = \left(\frac{\sqrt{2}}{2}\right)^2 + \left(\frac{\sqrt{2}}{2}\right)^2 = \frac{1}{2} + \frac{1}{2} = 1 $$

Errores comunes al calcular valores numéricos

Al calcular el valor numérico de funciones trigonométricas, es frecuente cometer errores que no siempre se deben a falta de conocimiento, sino a descuidos en el procedimiento. Reconocer estos errores ayuda a evitarlos y a mejorar la precisión en los cálculos.

Olvidar el signo del valor trigonométrico

Cuando los ángulos no están en el primer cuadrante, el signo de la función es tan importante como su valor absoluto.

• Un mismo ángulo de referencia puede tener valores positivos o negativos.
• Cada cuadrante tiene funciones que cambian de signo.

Recomendación:

Ubica siempre el ángulo en su cuadrante correspondiente antes de escribir el valor final.

No respetar el orden de operaciones

En expresiones con varias operaciones, algunos errores se producen por no seguir el orden correcto:

1. Paréntesis
2. Potencias y raíces
3. Multiplicación y división
4. Suma y resta

Recomendación:

Evalúa primero cada función trigonométrica, luego aplica el orden de las operaciones matemáticas.

Error al usar valores notables

Otro error común es recordar mal los valores de los ángulos notables o confundirlos entre sí.

Ejemplos frecuentes:

Escribir sen60°= 1/2 (incorrecto).

Confundir los valores de 30° y 60°.

Recomendación:

Aprende y repasa constantemente la tabla de valores notables, y evita usar aproximaciones si el ejercicio pide valores exactos.

Ejercicios propuestos

Solución:

$$ sen 150^\circ = \frac{1}{2}, \quad cos 300^\circ = \frac{1}{2}, \quad sec 60^\circ = 2, \quad csc 30^\circ = 2, \quad tan 45^\circ = 1, \quad cot 45^\circ = 1 $$

Sustituir cada valor numérico y operar

$$ \left( \frac{1}{\frac{1}{2}} + \frac{1}{\frac{1}{2}} \right) – \left( \frac{2^2}{2} \right) + \sqrt{ \frac{1^2}{1^2} } $$

Continuar con la operación

$$ (2 + 2) – \frac{4}{2} + \sqrt{1} $$

$$ 4 – 2 + 1 $$

Resultado

$$ 3 $$

Expresión dada y resultado

$$ \left( \frac{1}{sen 150^\circ} + \frac{1}{cos 300^\circ} \right) – \left( \frac{sec^2 60^\circ}{csc 30^\circ} \right) + \sqrt{ \frac{tan^2 45^\circ}{cot^2 45^\circ} }=3 $$

Solución:

$$ sen 300^\circ = -\frac{\sqrt{3}}{2}, \quad sec 240^\circ = -2, \quad cos 210^\circ = -\frac{\sqrt{3}}{2}, \quad csc 30^\circ = 2, \quad tan 330^\circ = -\frac{1}{\sqrt{3}}, \quad cot 45^\circ = 1 $$
$$ \frac{ \left( -\frac{\sqrt{3}}{2} \cdot -2 \right) – \left( -\frac{\sqrt{3}}{2} \cdot 2 \right) } { -\frac{1}{\sqrt{3}} + 1 } $$
$$ \frac{ \left( \sqrt{3} \right) – \left( -\sqrt{3} \right) } { 1 – \frac{1}{\sqrt{3}} } $$
$$ \frac{ 2\sqrt{3} }{ \frac{\sqrt{3}-1}{\sqrt{3}} } $$
$$ 2\sqrt{3} \cdot \frac{\sqrt{3}}{\sqrt{3}-1} $$
$$ \frac{6}{\sqrt{3}-1} $$
$$ \frac{6(\sqrt{3}+1)}{2} $$
$$ 3(\sqrt{3}+1) $$
$$ \frac{ \left( sen 300^\circ \cdot sec 240^\circ \right) – \left( cos 210^\circ \cdot csc 30^\circ \right) } { tan 330^\circ + cot 45^\circ }= 3(\sqrt{3}+1)$$

Solución

Obtener el valor numérico de cada función trigonométrica

$$ tan 210^\circ = \frac{1}{\sqrt{3}}, \quad cot 30^\circ = \sqrt{3}, \quad sec 330^\circ = \frac{2}{\sqrt{3}}, \quad csc 150^\circ = 2 $$

Reemplazar:
$$ \frac{ \frac{1}{\sqrt{3}} + \sqrt{3} } { \left( \frac{2}{\sqrt{3}} \right)(2) } $$

Operar en el numerador y denominador:
$$ \frac{ \frac{1 + 3}{\sqrt{3}} } { \frac{4}{\sqrt{3}} } $$

Dividir las fracciones:
$$ \frac{ \frac{4}{\sqrt{3}} } { \frac{4}{\sqrt{3}} } $$
$$ 1 $$

Expresión dada y resultado

$$ \frac{tan 210^\circ + cot 30^\circ}{sec 330^\circ \cdot csc 150^\circ}=1 $$

Solución:

1 Sustitución de valores numéricos de las funciones trigonométricas:

$$ sen 45^\circ = \frac{\sqrt{2}}{2}, \quad cos 45^\circ = \frac{\sqrt{2}}{2}, \quad tan 45^\circ = 1 $$
$$ sen 60^\circ = \frac{\sqrt{3}}{2}, \quad cos 30^\circ = \frac{\sqrt{3}}{2}, \quad sen 30^\circ = \frac{1}{2} $$

2 Sustitución en la expresión original:

$$ \left[\frac{\left(\frac{\sqrt{2}}{2}\right)^2 – \left(\frac{\sqrt{2}}{2}\right)^2}{1^2}\right] \cdot \left(\frac{\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2}}{\frac{1}{2}}\right) $$

3 Simplificar potencias y sumas:

$$ \left[\frac{\frac{2}{4} – \frac{2}{4}}{1}\right] \cdot \left(\frac{\frac{2\sqrt{3}}{2}}{\frac{1}{2}}\right) $$

4 Simplificar cada factor:

$$ \left[\frac{0}{1}\right] \cdot \left(\frac{\sqrt{3}}{\frac{1}{2}}\right) $$ $$ 0 \cdot 2\sqrt{3} $$

5 Resultado

$$ \left[\frac{sen^2 45^\circ – cos^2 45^\circ}{tan^2 45^\circ}\right] \cdot \left(\frac{sen 60^\circ + cos 30^\circ}{sen 30^\circ}\right)=0 $$

Actividades

Determina el valor numérico de las siguientes expresiones:

1. $$sen 30^\circ + tan^2 60^\circ=$$
2. $$cos 45^\circ – sen 30^\circ=$$
3. $$2 sen 60^\circ – cos 60^\circ=$$
4. $$tan 45^\circ + sen^2 30^\circ=$$
5. $$\frac{cos 60^\circ}{sen 30^\circ}=$$
6. $$ \left(\frac{sec 210^\circ}{cos 330^\circ}\right) – \left(\frac{csc 150^\circ}{sen 30^\circ}\right)= $$
7. $$ \frac{ \left(sen 330^\circ \cdot sec 210^\circ\right) – \left(cos 150^\circ \cdot csc 30^\circ\right) } { tan 315^\circ + cot 60^\circ }= $$

© LaProfeMatematik · Aprender con amor de Dios y mucha pasión