¿Te has preguntado alguna vez cómo la circunferencia está presente en el diseño de pistas circulares que crean los ingenieros o en los logos perfectamente redondeados que elaboran los diseñadores gráficos?
¿Te has preguntado alguna vez cómo la circunferencia está presente en el diseño de pistas circulares que crean los ingenieros o en los logos perfectamente redondeados que elaboran los diseñadores gráficos?
Detrás de todas esas formas se encuentra la circunferencia, una figura fundamental en la geometría analítica que conecta el arte visual con el razonamiento matemático.
En este post aprenderás qué es la circunferencia, cómo se obtiene su ecuación y cómo aplicarla en contextos reales, de manera clara, práctica y paso a paso. 🧮
¿Qué es una circunferencia?
En geometría analítica, la circunferencia es definida como el conjunto de todos los puntos de un plano situado a una misma distancia de un punto fijo, llamado centro. Esa distancia constante recibe el nombre de radio, y determina el tamaño de la circunferencia.
En otras palabras, si todos los puntos están exactamente a la misma distancia del centro, forman una figura perfectamente redonda: la circunferencia.
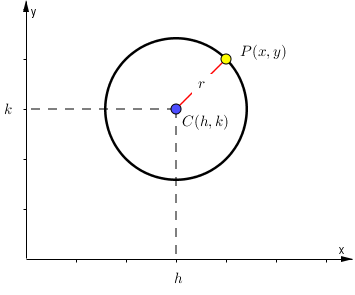
Donde:
C (h, k): Centro.
h y k : Coordenadas del centro.
P (x, y): Es el punto por donde pasa la circunferencia.
r : Radio.
Su ecuación más utilizada es llamada ecuación ordinaria:
$$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
Cuando el centro de la circunferencia está ubicado en el origen del plano cartesiano, su ecuación es: $$x^{2}+y^{2}=r^{2}$$
Ecuación ordinaria y ecuación general de la circunferencia
Al expandir la ecuación ordinaria, se obtiene la ecuación general de la circunferencia:
$$x^{2}+y^{2}+Dx+Ey+F=0$$
| Ecuación | Forma | Uso |
| $$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
| Ordinaria | Se usa cuando se conoce el centro y el radio. |
| $$x^{2}+y^{2}+Dx+Ey+F=0$$
| General | Es aplicado en cálculos y análisis algebraico. |
Cómo hallar el centro y el radio de una circunferencia en la ecuación general
A partir de la ecuación general$$x^{2}+y^{2}+Dx+Ey+F=0$$ Puedes obtener el centro y el radio, donde:
| $$D=-2h$$ $$E=-2k$$ $$F=h^{2}+k^{2}-r^{2}$$ |
Observación
Si $$D^{2}+E^{2}-4F> 0$$ La ecuación$$x^{2}+y^{2}+Dx+Ey+F=0$$ representa una circunferencia con centro (C) de coordenadas distintas a cero, es decir C (h, k).
Entonces, para calcular el centro (C) y el radio (r) debes aplicar:
| Centro | Radio |
| $$C\left ( h,k \right )$$ | $$r=\sqrt{h^{2}+k^{2}-F}$$ |
| $$C\left ( -\frac{D}{2}, -\frac{E}{2} \right )$$ | $$r=\frac{\sqrt{D^{2}+E^{2}-4F}}{2}$$ |
Aplicaciones de la circunferencia en la vida cotidiana
Las circunferencias no son solo figuras en la pizarra o en el cuaderno. En la vida cotidiana, aparecen en contextos que quizás no habías notado:
- Ingeniería civil: diseño de rotondas, túneles y estructuras circulares.
- Deportes: trazados en el campo de fútbol, análisis de trayectorias de pelotas o ruedas en movimiento.
- Astronomía: modelos de órbitas planetarias casi circulares.
- Diseño gráfico: construcción de logotipos y figuras simétricas.
Comprender esta figura plana te permite apreciar cómo las matemáticas está involucrada en muchas situaciones.
Ejercicios de la circunferencia resueltos paso a paso
Ejemplo # 1. ¿Cuál es la ecuación de la circunferencia con centro en el origen y radio de 4 unidades?
Solución:
Fórmula ordinaria: $$x^{2}+y^{2}=r^{2}$$
Al reemplazar:
$$x^{2}+y^{2}=4^{2}$$
$$x^{2}+y^{2}=16$$
$$x^{2}+y^{2}-16=0$$
Ejemplo # 2
Determine la ecuación de la circunferencia de centro en el origen y radio $$\frac{\sqrt{3}}{2}$$
Solución:
Fórmula ordinaria: $$x^{2}+y^{2}=r^{2}$$
Al sustituir:
$$x^{2}+y^{2}=\left ( \frac{\sqrt{3}}{2} \right )^{2}$$
$$x^{2}+y^{2}=\frac{3}{4}$$
Se transforma la expresión en forma lineal
$$4x^{2}+4y^{2}=3$$
Ecuación:
$$4x^{2}+4y^{2}-3=0$$
Ejemplo # 3
Determina la ecuación de la circunferencia de centro (1, −3) y radio de 2 unidades.
Solución:
Fórmula ordinaria:
$$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
Sustitución:
$$\left (x-1 \right )^{2}+\left ( y+3 \right )^{2}=2^{2}$$
Desarrollo:
$$x^{2}-2x+1+y^{2}+6y+9=4$$
$$x^{2}+y^{2}-2x+6y+6=0$$
Ecuación de la circunferencia
$$x^{2}+y^{2}-2x+6y+6=0$$
Ejemplo # 4
Calcular la ecuación de la circunferencia de centro en el plano (-1/2, -5/6) y radio 5/6 unidades.
Solución:
Fórmula ordinaria:
$$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
Al sustituir los valores queda así:
$$\left (x+\frac{1}{2} \right )^{2}+\left ( y+\frac{5}{6} \right )^{2}=\left ( \frac{5}{6} \right )^{2}$$
Se aplica productos notables, potenciación y se iguala a cero:
$$x^{2}+x+\frac{1}{4}+y^{2}+\frac{5y}{3}+\frac{25}{36}=\frac{25}{36}$$
$$x^{2}+y^{2}+x+\frac{5y}{3}+\frac{1}{4}=0$$
Se saca mínimo común múltiplo (m.c.m.) a los denominadores:
m.c.m.=12
$$\frac{12x^{2}+12y^{2}+12x+20y+3}{12}=0$$
Despeje:
$$12x^{2}+12y^{2}+12x+20y+3=0$$
Ecuación:
$$12x^{2}+12y^{2}+12x+20y+3=0$$
Ejemplo # 5
¿Cuál es la ecuación de la circunferencia de centro en el origen y que pasa por el punto (2, −3)?
Solución:
Calculo del radio aplicando la fórmula de la distancia entre dos puntos:
$$d=r=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$
Sustitución de las coordenadas del punto y centro:
$$d=r=\sqrt{(2-0)^{2}+(-3-0)^{2}}=\sqrt{13}$$
Cálculo de la ecuación:
$$x^{2}+y^{2}=r^{2}$$
$$x^{2}+y^{2}=\left ( \sqrt{13} \right )^{2}$$
$$x^{2}+y^{2}=13$$
$$x^{2}+y^{2}-13=0$$
Ecuación de la circunferencia:
$$x^{2}+y^{2}-13=0$$
Ejemplo # 6
Hallar la ecuación de la circunferencia de diámetro el segmento formado por los puntos A(−4,7) 𝑦 𝐵(6,−1).
Solución:
Punto medio del diámetro es igual al punto centro de la circunferencia:
$$C=\left ( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right )$$
Reemplazar las coordenadas de ambos puntos:
$$C=\left ( \frac{-4+6}{2},\frac{7-1}{2} \right )$$
Centro de la circunferencia:
$$C\left ( 1,3 \right )$$
Cálculo del radio:
B(6,-1); C(1,3)
$$r=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$
Ecuación ordinaria:
$$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
Sustitución:
$$\left (x-1 \right )^{2}+\left ( y-3 \right )^{2}=(\sqrt{41})^{2}$$
$$(x-1)^{2}+(y-3)^{2}=41$$
$$x^{2}+y^{2}-2x-6y-31=0$$
Gráfica:
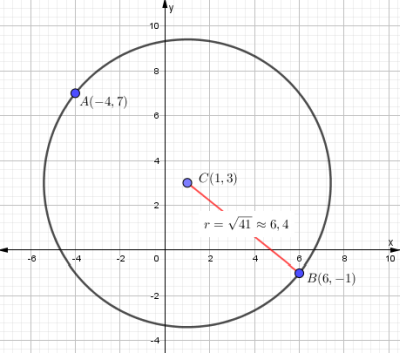
Ecuación de la circunferencia:
$$x^{2}+y^{2}-2x-6y-31=0$$
Ejemplo # 7
Determine la ecuación de la circunferencia de diámetro en el punto (−3,5) y (7, −3).
Solución:
Punto medio del diámetro es igual al punto centro de la circunferencia:
$$C=\left ( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right )$$
$$C=\left ( \frac{-3+7}{2},\frac{5-3}{2} \right )$$
$$C\left ( 2,1 \right )$$
Cálculo del radio:
A(−3,5); C(2,1)
$$r=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$
Ecuación ordinaria:
$$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
Sustitución:
$$\left (x-2 \right )^{2}+\left ( y-1 \right )^{2}=(\sqrt{41})^{2}$$
$$\left ( x-2 \right )^{2}+\left ( y-1 \right )^{2}=41$$
$$x^{2}+y^{2}-4x-2y-36=0$$
Ecuación de la circunferencia:
$$x^{2}+y^{2}-4x-2y-36=0$$
Ejemplo # 8
Determinar la ecuación de la circunferencia de centro en el punto (1, −3) que pasa por el punto (4,3).
Solución:
Se aplica la fórmula de la distancia entre dos puntos:
$$d=r=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$
Ecuación ordinaria:
$$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
$$\left (x-1 \right )^{2}+\left ( y+3 \right )^{2}=\left ( 3\sqrt{5} \right )^{2}$$
$$(x-1)^{2}+(y+3)^{2}=45$$
$$x^{2}+y^{2}-2x+6y-35=0$$
Ecuación de la circunferencia:
$$x^{2}+y^{2}-2x+6y-35=0$$
Ejemplo # 9
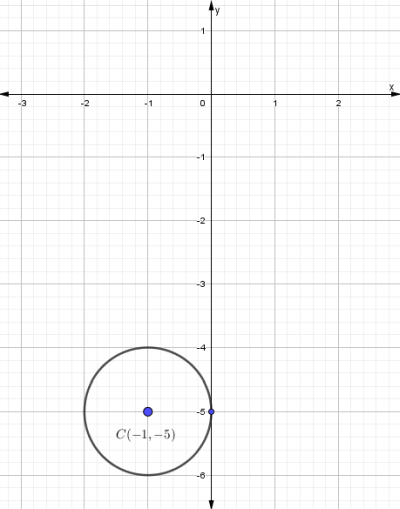
¿Cuál es la ecuación de la circunferencia cuyo centro está en C(−1, −5) y es tangente al eje «y»?
Solución:
Se grafica el centro C(-1,-5)
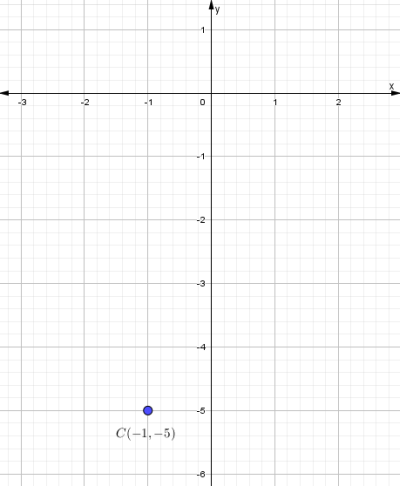
Como es tangente al eje “y” su radio es:$$r=1$$
Como se tiene el radio y centro, se aplica la ecuación ordinaria:
$$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
$$\left (x+1 \right )^{2}+\left ( y+5 \right )^{2}=1$$
$$x^{2}+y^{2}+2x+10y+25=0$$
Ecuación de la circunferencia:
$$x^{2}+y^{2}+2x+10y+25=0$$
Gráfica:
Ejemplo # 10
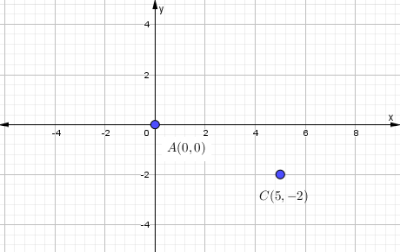
El centro de una circunferencia es el punto (5, −2) y pasa por el origen. ¿Cuál es su ecuación?
Solución:
Se grafican los datos dados:
Cálculo del radio:
$$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
$$\left (0-5 \right )^{2}+\left ( 0+2 \right )^{2}=r^{2}$$
$$25+4=r^{2}$$
$$r=\sqrt{29}$$
Cálculo de la ecuación:
$$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
$$(x-5)^{2}+(y+2)^{2}=29$$
$$x^{2}+y^{2}-10x+4y=0$$
Ecuación de la circunferencia:
$$x^{2}+y^{2}-10x+4y=0$$
Ejemplo # 11
Obtén la ecuación de la circunferencia de centro en el punto (−4,2) y diámetro 8 unidades.
Solución:
Radio:
$$r=\frac{d}{2}=\frac{8}{2}=4$$
Cálculo de la ecuación aplicando la ecuación ordinaria:
$$\left (x-h \right )^{2}+\left ( y-k \right )^{2}=r^{2}$$
$$\left (x+4 \right )^{2}+\left ( y-2 \right )^{2}=16$$
$$x^{2}+y^{2}+8x-4y+4=0$$
Ecuación de la circunferencia:
$$x^{2}+y^{2}+8x-4y+4=0$$
Ejemplo # 12
Una circunferencia tiene su centro en (0, −2) y es tangente a la recta 5𝑥 − 12𝑦 + 2 = 0 ¿Cuál es su ecuación?
Solución:
Graficar los puntos dados:
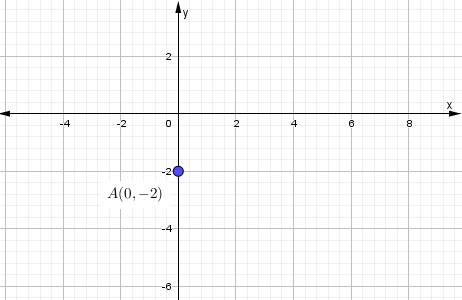
Conclusión: Como es tangente a una recta y se tiene el centro A(0,-2), se calcula el radio que va desde el centro hasta el punto tangente a la recta, es decir se aplica la fórmula de la distancia entre un punto a una recta.
Cálculo del radio, aplicando la fórmula de la distancia de un punto a una recta.
$$d=r=\frac{\left | Ax_{1}+By_{1}+C\right |}{\sqrt{A^{2}+B^{2}}}$$
Cálculo de la ecuación:
$$x^{2}+(y+2)^{2}=4$$
$$x^{2}+y^{2}+4y=0$$
Ecuación:
$$x^{2}+y^{2}+4y=0$$
Ejemplo # 13
Una circunferencia tiene su centro en (4, −3) y es tangente a la recta 3𝑥 + 4𝑦 − 10 = 0 ¿Cuál es su ecuación?
Solución:
Cálculo del radio aplicando la fórmula distancia de un punto a una recta:
$$d=r=\frac{\left | Ax_{1}+By_{1}+C\right |}{\sqrt{A^{2}+B^{2}}}$$
Cálculo de la ecuación aplicando la ecuación ordinaria:
$$(x-4)^{2}+(y+3)^{2}=4$$
$$x^{2}+y^{2}-8x+6y+21=0$$
Ecuación:
$$x^{2}+y^{2}-8x+6y+21=0$$
Ejemplo # 14
Una circunferencia tiene su centro en (−2,3) y es tangente a la recta 20𝑥 − 21𝑦 − 42 = 0 ¿Cuál es su ecuación?
Solución:
Radio:
$$ r=\frac{\left | Ax_{1}+By_{1}+C\right |}{\sqrt{A^{2}+B^{2}}}$$
Ecuación:
$$(x+2)^{2}+(y-3)^{2}=25$$
$$x^{2}+y^{2}+4x-6y-12=0$$
Ecuación:
$$x^{2}+y^{2}+4x-6y-12=0$$
Ejemplo # 15
Hallar la ecuación de una circunferencia que pasa por los puntos D(3,4); C(11,4) y B(7,-4)
Solución:
Como los tres puntos están en la circunferencia$$x^{2}+y^{2}+Dx+Ey+F=0$$Dicha ecuación se cumple para cada uno de los puntos.
Parte # 1
Sustitución de cada punto en la ecuación general:
D(3,4)
$$3^{2}+4^{2}+D(3)+E(4)+F=0$$
$$9+16+3D+4E+F=0$$
$$3D+4E+F=-25$$
C(11,4)
$$11^{2}+4^{2}+D(11)+E(4)+F=0$$
$$121+16+11D+4E+F=0$$
$$11D+4E+F=-137$$
B(7,-4)
$$7^{2}+(-4)^{2}+D(7)+E(-4)+F=0$$
$$49+16+7D-4E+F=0$$
$$7D-4E+F=-65$$
Parte # 2
Se forma un sistema de tres ecuaciones lineales, el cual se resuelve aplicando la Regla de Cramer para determinar los valores de 𝐷, 𝐸 y 𝐹.
Sistema de ecuaciones dado:
$$
\begin{cases}
3D + 4E + F = -25 \\[4pt]
11D + 4E + F = -137 \\[4pt]
7D – 4E + F = -65
\end{cases}
$$
1. Cálculo del determinante principal
$$
\Delta =
\begin{vmatrix}
3 & 4 & 1 \\
11 & 4 & 1 \\
7 & -4 & 1
\end{vmatrix}
$$
Aplicando la regla de Sarrus:
\begin{aligned}
\Delta &= 4\cdot11\cdot1 + 1\cdot4\cdot7 + 1\cdot(-4)\cdot3 \\[4pt]
&\quad -\big(4\cdot1\cdot7 + 3\cdot4\cdot1 + 11\cdot(-4)\cdot1\big) \\[4pt]
&= (44 + 28 – 12) – (28 +12-44 ) \\[4pt]
&= 60 +4 = 64
\end{aligned}
$$
$$\boxed{\Delta = 64}$$
2. Cálculo de ΔD
$$
\Delta_D =
\begin{vmatrix}
-25 & 4 & 1 \\
-137 & 4 & 1 \\
-65 & -4 & 1
\end{vmatrix}
$$
\begin{aligned}
\Delta_D &= 4\cdot(-137)\cdot1 + 1\cdot4\cdot(-65) + 1\cdot(-4)\cdot(-25) \\[4pt]
&\quad -\big(4\cdot1\cdot(-65) + (-25)\cdot4\cdot1 + (-137)\cdot(-4)\cdot1\big) \\[4pt]
&= (-548 – 260 + 100) – (-260 – 100 + 548) \\[4pt]
&= -708 – 188 = -896
\end{aligned}
$$
$$\boxed{\Delta_D = -896}$$
3. Cálculo de ΔE
$$
\Delta_E =
\begin{vmatrix}
3 & -25 & 1 \\
11 & -137 & 1 \\
7 & -65 & 1
\end{vmatrix}
$$
\begin{aligned}
\Delta_E &= -25\cdot11\cdot1 + 1\cdot(-137)\cdot7 + 1\cdot(-65)\cdot3 \\[4pt]
&\quad -\big(-25\cdot1\cdot7 + 3\cdot(-137)\cdot1 + 11\cdot(-65)\cdot1\big) \\[4pt]
&= (-275 -959 – 195) – (-175 – 411 – 715) \\[4pt]
&= -1429 +1301) = -128
\end{aligned}
$$
$$\boxed{\Delta_E = -128}$$
4. Cálculo de ΔF
$$
\Delta_F =
\begin{vmatrix}
3 & 4 & -25 \\
11 & 4 & -137 \\
7 & -4 & -65
\end{vmatrix}
$$
\begin{aligned}
\Delta_F &= 4\cdot11\cdot(-65) + (-25)\cdot4\cdot7 + (-137)\cdot(-4)\cdot3 \\[4pt]
&\quad -\big(4\cdot(-137)\cdot7 + 3\cdot4\cdot(-65) + 11\cdot(-4)\cdot(-25)\big) \\[4pt]
&= (-2860 – 700 + 1644) – (-3836 – 780 +1100) \\[4pt]
&= -1916 – (-3516) \\[4pt]
&= -1916 + 3516 = 1600
\end{aligned}
$$
$$\boxed{\Delta_F = 1600}$$
5. Aplicación de la Regla de Cramer
$$
D = \dfrac{\Delta_D}{\Delta}, \quad
E = \dfrac{\Delta_E}{\Delta}, \quad
F = \dfrac{\Delta_F}{\Delta}
$$
$$
\begin{aligned}
D &= \dfrac{-896}{64} = -14, \\[6pt]
E &= \dfrac{-128}{64} = -2, \\[6pt]
F &= \dfrac{1600}{64} = 25
\end{aligned}
$$
Se tiene que:
$$\boxed{D = -14, \quad E = -2, \quad F = 25}$$
Resultado
$$x^{2}+y^{2}-14x-2y+25=0$$
Ejemplo # 16
Hallar la ecuación de la circunferencia que pasa por los puntos A(2,5); B(6,3) y C(2,-5)
Solución:
Para hallar la ecuación de la circunferencia, se requieren el centro (h, k) y el radio $(r)$. Dado que el centro equidista de los puntos de la circunferencia, este se sitúa sobre la mediatriz de cualquier segmento (cuerda) que una dos de esos puntos. La intersección de las mediatrices de dos cuerdas distintas define el centro de la circunferencia.
Se grafica y se unen los puntos A y B, B y C para comprender mejor la situación.
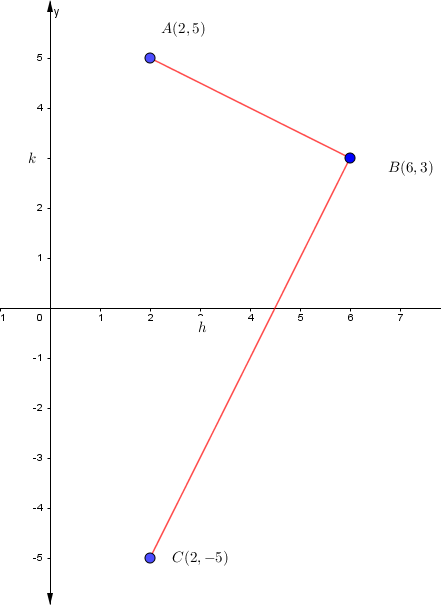
Calculo de la ecuación de la mediatriz del segmento AB
Determinar el punto medio:
A(2,5); B(6,3)
$$M=\left ( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right )$$
$$M=\left ( \frac{6+2}{2},\frac{3+5}{2} \right )=(4,4)$$
$$M(4,4)$$
Cálculo de la pendiente de la recta de la mediatriz:
Pendiente del segmento AB:
A(2,5); B(6,3)
$$m_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$m_{1}=\frac{3-5}{6-2}=\frac{-2}{4}=-\frac{1}{2}$$
$$m_{1}=-\frac{1}{2}$$
Pendiente de la mediatriz:
$$m_{2}=-\frac{1}{m_{1}}=-\frac{1}{-\frac{1}{2}}=2$$
$$m_{2}=2$$
Ecuación punto-pendiente
$$M(4,4);m=2$$
$$y-y_{1}=m(x-x_{1})$$
$$y-4=2(x-4)$$
$$y=2x-8+4$$
Resultado:
$$y=2x-4$$
Calculo de la ecuación de la mediatriz del segmento BC
Punto medio:
B(6,3); C(2,-5)
$$P=\left ( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right )$$
$$P=\left ( \frac{2+6}{2},\frac{-5+3}{2} \right )=(4,-1)$$
$$P(4,-1)$$
Pendiente de la mediatriz
Pendiente del segmento BC:
B(6,3); C(2,-5)
$$m_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$m_{1}=\frac{-5-3}{2-6}=\frac{-8}{-4}=2$$
$$m_{1}=2$$
Pendiente de la mediatriz:
$$m_{2}=-\frac{1}{m_{1}}=-\frac{1}{2}$$
$$m_{2}=-\frac{1}{2}$$
Ecuación punto-pendiente
$$P(4,-1);m=-\frac{1}{2}$$
$$y-y_{1}=m(x-x_{1})$$
$$y+1=-\frac{1}{2}(x-4)$$
$$y=-\frac{1}{2}x+2-1$$
$$y=-\frac{1}{2}x+1$$
Resultado:
$$y=-\frac{1}{2}x+1$$
Puntos medios graficados:
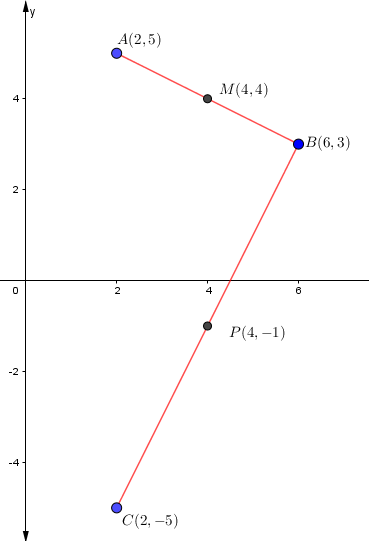
Establecer un sistema de ecuaciones para determinar el punto (centro de la circunferencia) donde se intersecan ambas mediatrices
Se aplica el método de reducción:
$$
\begin{array}{rl}
\!\!\!\!\!\!\!^{-1}\! &
\left\{
\begin{array}{l}
y = 2x – 4 \\
y = -\tfrac{1}{2}x + 1
\end{array}
\right.
\end{array}
$$
$$
\begin{array}{rcl}
-y &=& -2x + 4 \\[4pt]
\,y &=& -\tfrac{1}{2}x + 1 \\[4pt]
\hline
0 &=& -\tfrac{5}{2}x + 5
\end{array}
$$
$$\frac{5}{2}x=5$$
$$x=\frac{10}{5}$$
$$x=2$$
Reemplazar $$x=2$$En la primera ecuación y así obtener el valor de “y”
$$y=2(2)-4$$
$$y=0$$
Centro de la circunferencia$$I(2,0)$$
Cálculo del radio
$$I(2,0);C(2,-5)$$
$$r=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$
$$r=\sqrt{(2-2)^{2}+(-5-0)^{2}}=\sqrt{25}=5$$
Ecuación de la circunferencia
$$r^{2}=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$
$$5^{2}=\sqrt{(x-2)^{2}+(y-0)^{2}}$$
$$25=x^{2}-4x+4+y^{2}$$
$$x^{2}+y^{2}-4x+4-25=0$$
$$x^{2}+y^{2}-4x-21=0$$
Resultado:
$$x^{2}+y^{2}-4x-21=0$$
Gráfica:
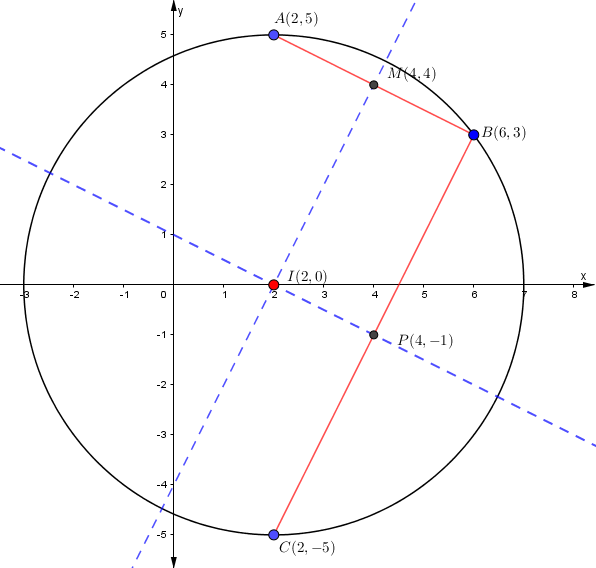
¿Quieres practicar más la circunferencia con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión