¿Sabías que graficar en el plano cartesiano puede ser tan fácil como medir el desempeño de un atleta? Imagina que un corredor participa en una competencia de 100 metros planos y, con ayuda de un cronómetro, registras el tiempo que tarda cada 5 metros. Al anotar esos datos y llevarlos al plano cartesiano, podrás representar visualmente su velocidad y analizar su rendimiento de forma clara y atractiva. ¡Así de sencillo es transformar números en una historia gráfica llena de movimiento!
¿Sabías que graficar en el plano cartesiano puede ser tan fácil como medir el desempeño de un atleta? Imagina que un corredor participa en una competencia de 100 metros planos y, con ayuda de un cronómetro, registras el tiempo que tarda cada 5 metros. Al anotar esos datos y llevarlos al plano cartesiano, podrás representar visualmente su velocidad y analizar su rendimiento de forma clara y atractiva. ¡Así de sencillo es transformar números en una historia gráfica llena de movimiento!
Plano cartesiano
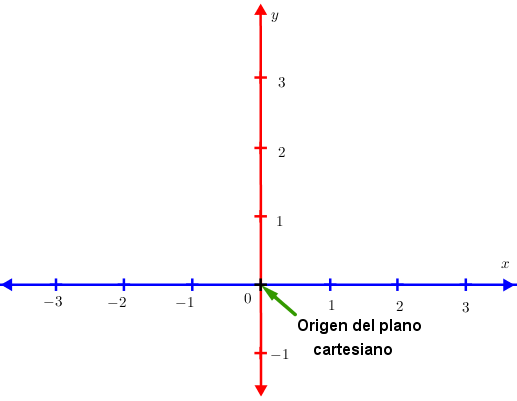
El plano cartesiano, también conocido como sistema de coordenadas rectangulares, es una herramienta fascinante que nos permite ubicar puntos y representar relaciones entre números de forma visual. Está formado por dos líneas que se cruzan en ángulo recto, llamadas ejes de coordenadas: una horizontal, conocida como eje X o de las abscisas, y otra vertical, llamada eje Y o de las ordenadas. Cada eje tiene una escala numérica, donde los valores positivos se ubican a la derecha y hacia arriba del origen, mientras que los negativos se sitúan a la izquierda y hacia abajo. Este sistema es la base para graficar funciones, representar movimientos y dar vida a los datos. ¡Observa la figura y descubre cómo se organiza este espacio matemático!

El punto donde se cruzan el eje X y el eje Y se conoce como el origen de coordenadas. Es el corazón del plano cartesiano, el lugar donde todo comienza y donde ambos ejes marcan el valor cero (0). A partir de este punto se ubican todos los demás valores positivos y negativos del plano. ¡Observa con atención y verás cómo desde el origen se construye todo el sistema de coordenadas!
Cuando los dos ejes se cruzan perpendicularmente, el plano se divide en cuatro regiones llamadas cuadrantes. Cada cuadrante tiene su propio conjunto de valores positivos y negativos, y se enumeran en sentido contrario a las agujas del reloj. Esta organización permite identificar con precisión la ubicación de cualquier punto dentro del plano cartesiano.

Resumen de las características del plano cartesiano
El plano cartesiano tiene varias características que lo hacen único y muy útil para representar relaciones matemáticas. Aquí te las explico de forma sencilla:
- Es un plano bidimensional (2D), ya que tiene dos dimensiones: ancho y alto.
- Está formado por dos ejes, uno horizontal (eje X) y otro vertical (eje Y).
- Ambos ejes se cruzan formando un ángulo recto de 90°.
- En el punto donde se interceptan los ejes se encuentra el origen del plano, representado con el número cero (0).
- La intersección de los ejes divide el plano en cuatro cuadrantes, que se enumeran en sentido contrario a las agujas del reloj.
- Cada eje debe tener una escala numérica para ubicar correctamente los puntos.
- Tomando como referencia el origen, en el eje X los números positivos se encuentran a la derecha y los negativos a la izquierda; mientras que en el eje Y los positivos están arriba y los negativos abajo.
Así, el plano cartesiano se convierte en una guía perfecta para explorar el mundo de las coordenadas y las representaciones gráficas.
¿Cómo construir un plano cartesiano?
Construir un plano cartesiano es el primer paso para entender cómo se representan los puntos, figuras y movimientos en el espacio. Solo necesitas trazar dos líneas que se crucen en ángulo recto: una horizontal, llamada eje X, y otra vertical, llamada eje Y. En el punto donde se encuentran, conocido como origen, todo comienza. A partir de allí, podrás dividir el plano en cuatro cuadrantes, asignar valores positivos y negativos y empezar a graficar relaciones y situaciones de la vida real. ¡Es como crear un mapa matemático donde cada punto tiene su lugar exacto!..
A continuación los pasos para su construcción:
Primero
Consigue una hoja de papel milimetrado o cuadriculado para facilitar la ubicación de los puntos.
Segundo
Ten a la mano una regla y, si lo deseas, un transportador para asegurar la perpendicularidad de los ejes.
Tercero
Coloca la regla en posición horizontal donde desees iniciar el trazo y dibuja una línea recta: será el eje de las abscisas (eje X).
Cuarto
Agrega una flecha en cada extremo del eje X para indicar su continuidad hacia la derecha y hacia la izquierda.

Quinto
Desde el punto central de la recta (que será el origen), marca una pequeña línea cada centímetro con ayuda de la regla, tanto a la derecha como a la izquierda.

Sexto
Escribe los números de la escala: los positivos hacia la derecha del origen y los negativos hacia la izquierda.

Séptimo
Ahora, coloca la regla verticalmente sobre el origen (0) y traza la línea del eje de las ordenadas (eje Y).

Si estás trabajando en una hoja blanca, utiliza el transportador: coloca su centro en el origen y marca un punto en 90° para garantizar la perpendicularidad.
Gira el transportador realiza el mismo procedimiento anterior.
Une los puntos con la regla para formar el eje Y.
Octavo
Marca los intervalos de un centímetro en ambos sentidos, enumera la escala positiva hacia arriba y la negativa hacia abajo y dibuja las flechas del eje Y en ambos extremos, hacia arriba y hacia abajo.

Noveno
Verifica que ambos ejes se crucen exactamente en el punto (0,0), conocido como origen del plano cartesiano.
Finalidad del plano cartesiano
La principal finalidad del plano cartesiano es ubicar y representar puntos mediante un par ordenado. Gracias a este sistema, podemos mostrar de forma visual la posición exacta de cualquier punto en el plano.
Cada punto se identifica con una letra mayúscula y se expresa con dos coordenadas entre paréntesis, por ejemplo: (x, y).
- La primera coordenada (x) indica la posición sobre el eje horizontal o eje X.
- La segunda coordenada (y) señala la ubicación sobre el eje vertical o eje Y.
Ejemplo:
Si tienes el punto P(-3, 5), su par ordenado es (-3, 5).
Esto significa que el punto P está ubicado 3 unidades a la izquierda del origen (por el -3 en el eje X) y 5 unidades hacia arriba (por el 5 en el eje Y).
¿Cómo graficar puntos en el plano cartesiano?
Para graficar puntos en el plano cartesiano, es importante observar con atención las coordenadas del par ordenado, ya que cada número indica una posición exacta en los ejes. Sigue estos pasos sencillos:
- Identifica la primera coordenada (x).
Desde el origen, muévete hacia la derecha si el valor es positivo o hacia la izquierda si es negativo. Luego, traza una línea segmentada vertical suave desde ese punto. - Ubica la segunda coordenada (y).
Desde el origen, sube si el valor es positivo o baja si es negativo, y traza una línea segmentada horizontal suave. - Marca el punto de intersección.
El lugar donde se cruzan ambas líneas corresponde a la ubicación del punto en el plano. - Escribe el nombre del punto.
Coloca junto al punto su letra mayúscula de identificación, por ejemplo A(x, y).
Así, podrás representar fácilmente cualquier punto y visualizar su posición dentro de los cuadrantes del plano cartesiano.
Ejemplos de gráfico de puntos paso a paso
1.Representa en el plano cartesiano los siguientes puntos:
| A(-2,2) | B(0,5) | C(-3,-3) |
- ¿Diga en qué cuadrante está cada uno de los puntos?
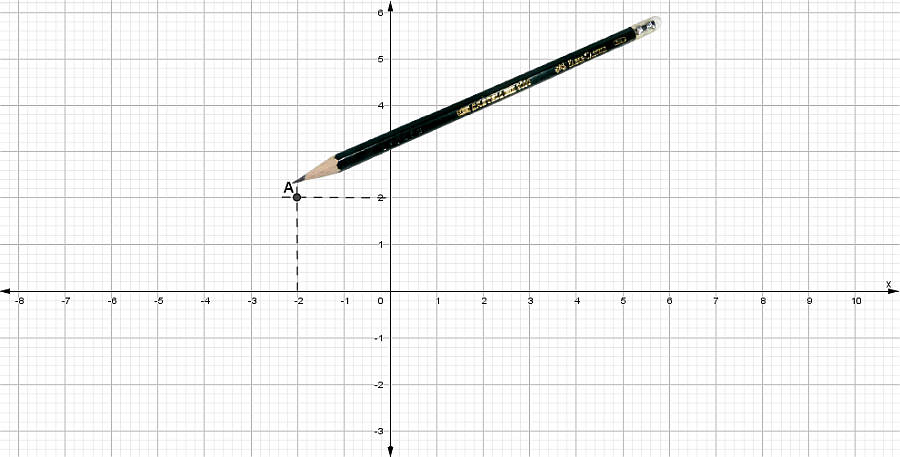
Primer Punto
A (-2,2)
- El valor de la primera componente es x = –2 .
Por ser valor de x se traza una línea vertical segmentada desde x = –2 hasta la cercanía de la otra coordenada y = 2

- El valor de la segunda componente es y = 2 .
Por ser valor de y se traza una línea horizontal segmentada desde y = 2 hasta la cercanía de la otra coordenada x = 2

- Marcar un punto donde ambas líneas se intersecan.
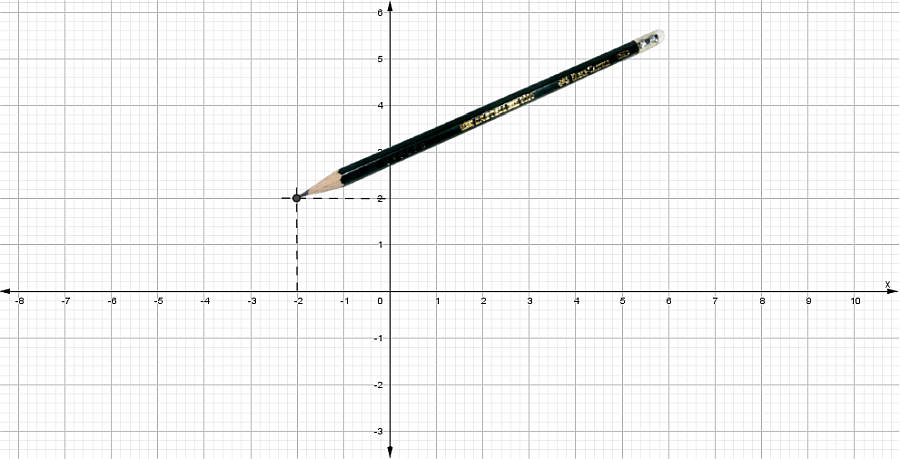
- Escribe el nombre del punto.
Segundo punto
B (0,5)
- El valor de la primera componente es x = 0
Por ser valor de x se traza una línea vertical segmentada desde x = 0 hasta la cercanía de la otra coordenada
y = 5, pero la línea coincidiría con el eje “y” por lo tanto se marca el punto en y = 5
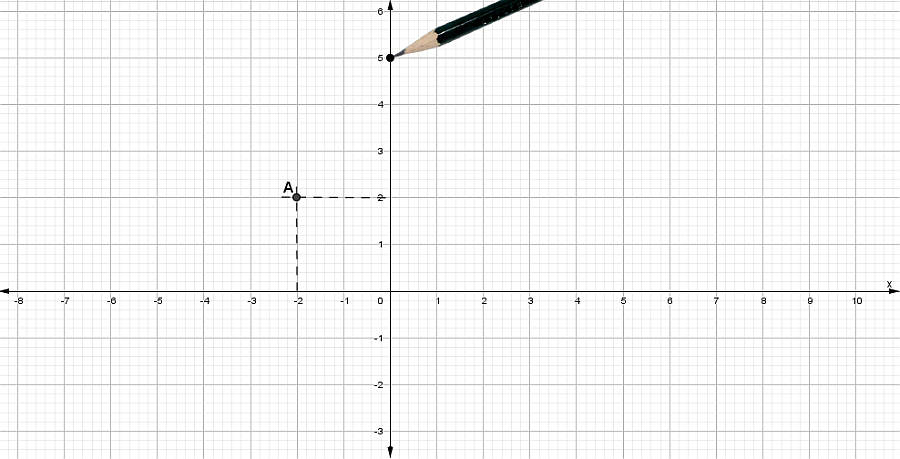
- Escribe el nombre del punto.

Tercer punto
C (-3,3)
- El valor de la primera componente es x = –3
Por ser valor de x se traza una línea vertical segmentada desde x = –3 hasta la cercanía de la otra coordenada
y = 3
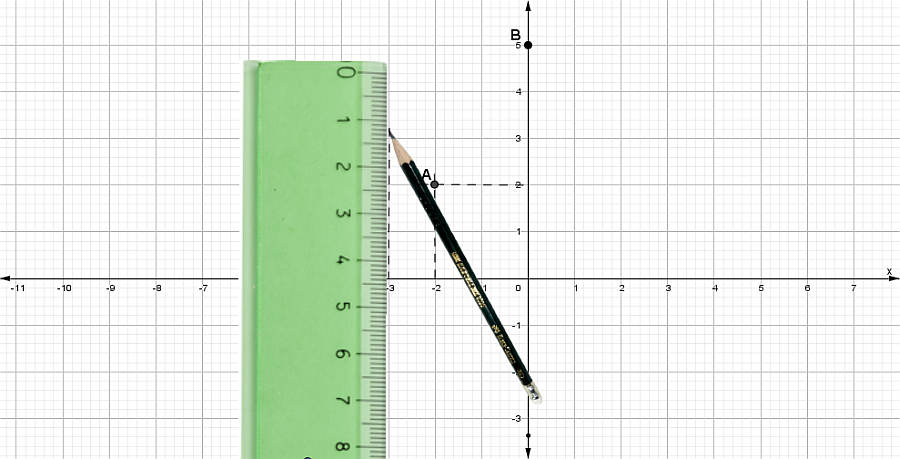
- El valor de la segunda componente es y = 3 .
Por ser valor de y se traza una línea horizontal segmentada desde y = 3 hasta la cercanía de la otra coordenada
x = -3
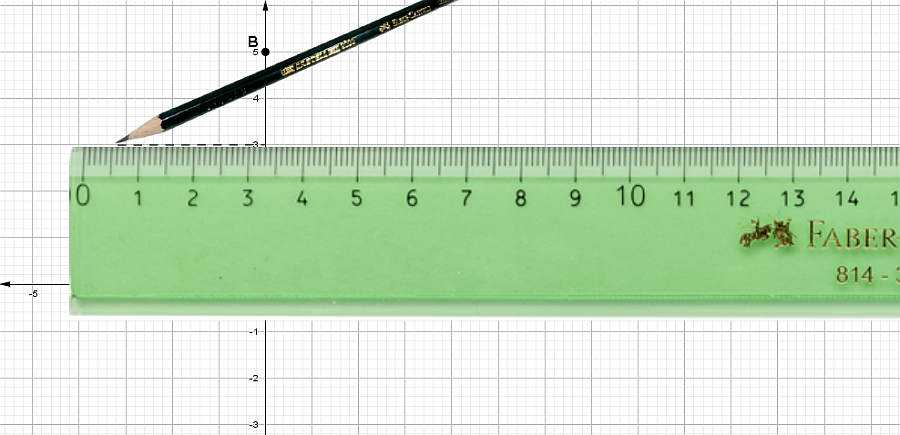
- Escribir el nombre del punto.

Finalmente los tres puntos graficados quedan así:
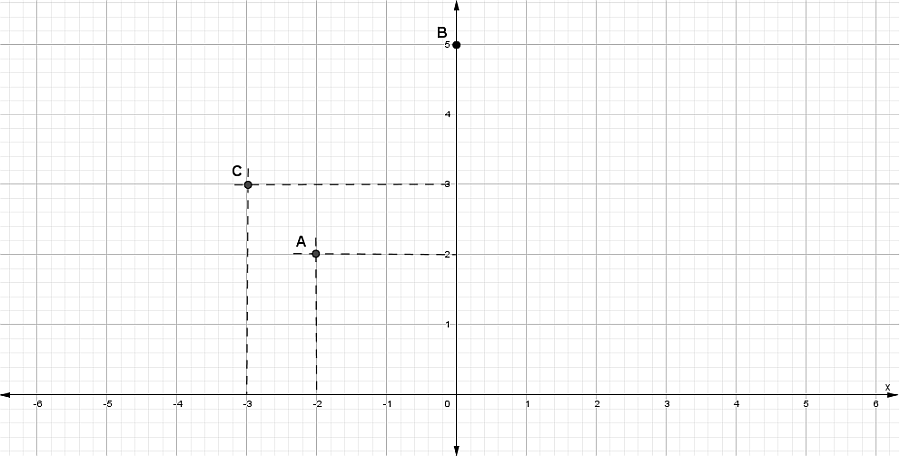
Los puntos A y C quedaron ubicados en el II cuadrante, mientras que el punto B quedó en todo el eje positivo de “y”
Video-Tutorial
En el siguiente video descubrirás, paso a paso, cómo graficar una figura con forma de bota utilizando puntos en el plano cartesiano. Aprenderás de manera visual y divertida cómo cada par ordenado da forma a un dibujo completo. ¡Prepárate para conectar las coordenadas y ver cómo los puntos cobran vida!
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
1.Representa en el plano cartesiano los siguientes puntos.
| A (-3,0) | B (0 ,-5) | C (-4 , 5) | D (-1 , 2) |
| E (4 , 1) | F (0,0) | G (1, -1) | H (-5 ,5) |
2.¿En cuál cuadrante está cada uno de los puntos de la actividad anterior?
3.Represente los siguientes puntos en el I cuadrante, luego una cada punto y diga que figura se formó.
| A(0,8) | B(0,12) | C(3,15) | D(5,15) | E(5,14) | F(3,12) | G(2,12) |
| H(2,9) | I(4,11) | J(6,11) | K(8,9) | L(8,13) | M(10,11) | N(14,11) |
| O(16,13) | P(16,7) | Q(15,6) | R(13,5) | S(11,5) | T(9,6) | U(8,7) |
| V(8,4) | W(9,4) | X(9,2) | Y(6,2) | Z(6,6) | AA(4,6) | AB(3,5) |
| AC(3,4) | AD(5,4) | AE(5,2) | AF(1,2) | AG(0,8) | AH(9,8) | AI(9,10) |
| AJ(11,10) | AK(11,8) | AL(9,8) | AM(13,10) | AN(15,10) | AO(15,8) | AP(13,8) |
| AQ(13,10) | AR(11,7) | AS(12,8) | AT(13,7) | AU(11,7) |
Si te gustó este contenido no olvides compartir, coméntanos y dinos qué te gustaría que añadiéramos a nuestro blog.
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión