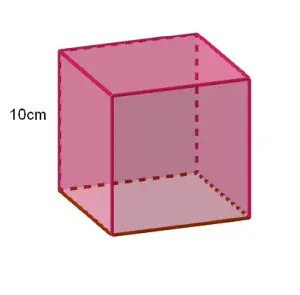
Si estás buscando las propiedades de la potenciación de números enteros has llegado al lugar indicado. En nuestra vida cotidiana el uso de estas propiedades se hace con mucha frecuencia. Aunque no lo notes, en este post te darás cuenta lo importante de saber su aplicación. Por ejemplo, al calcular el volumen de una caja debes aplicar la siguiente fórmula:
Si cada lado de la caja mide 10 cm, los pasos para calcular el volumen es el siguiente:
- Sustituir el valor de 10cm y se elevarlo a la tres:
- Aplica una propiedad de la potenciación:
- Como el 10 está elevado a la tres, se multiplica tres veces:
Finalmente el volumen de la caja es:
¿Qué propiedad de la potenciación de números enteros se aplicó en esta situación?
Propiedades de la potenciación de números enteros
La potenciación es una operación matemática que consiste en multiplicar un número por sí mismo llamado «base» según lo que exprese el exponente. La potenciación se puede presentar de diversas formas y para poderlas resolver correctamente, es fundamental aplicar las propiedades de la potenciación. A continuación, se detallan cada una de estas propiedades.
1. Multiplicación de potencias de igual base
En esta propiedad, se escribe la misma base y se suman los exponetes. En este caso las bases (a) son iguales y se multiplican, cada base posee un exponente (m) y (n) y el resultado es la misma base (a) y el exponente resultante es la sumatoria de los exponentes de cada base. Observe la expresión de la primera propiedad:
$$a^{m}.a^{n}=a^{m+n}$$
Ejemplo: A continuación se expresa una multiplicación de dos bases iguales de valor 3 con exponentes 5 y 3 . Se aplica entonces la primera propiedad de la potenciación y queda de la siguiente manera:
$$3^{5}.3^{3}=3^{5+3}=3^{8}$$
Finalmente se resuelve la potenciación:
$$3^{8}=3.3.3.3.3.3.3.3=6561$$
2. Potencia de una potencia
En este caso la base (a), posee un exponente (m) y a su vez este exponente posee otro exponente (n) el resultado es la base (a) y el exponente resultante es la multiplicación de los exponentes. Observe la expresión de la tercera propiedad:
$$(a^{m})^{n}=a^{n}$$
Ejemplo: A continuación se expresa una base igual a 4 elevado al cuadrado y a su vez es elevado al cubo. Se aplica entonces la tercera propiedad de la potenciación y queda de la siguiente manera:
$$(4^{2})^{3} = 4^{2.3} = 4^{6}$$
Finalmente se resuelve la potenciación
$$4^{6}=4.4.4.4.4.4 = 4096$$
3. Potencia de base 10
La forma de resolver esta situación es escribiendo la base diez y agregarle tantos ceros según lo indicado por el exponente.
Ejemplo:
Para resolver $$10^{2}$$ el procedimiento es multiplicar la base dos veces, es decir: $$10^{2}=10.10=100$$
$$10^{2}=100$$
4. Potencia de un producto
En este caso ambas bases (a y b) se multiplican son diferentes y están elevadas.
Para resolverlo debes multiplicar el exponente (n) por el exponente de cada base (a y b), finalmente resuelve ambas potencias y multiplicas ambos resultados.
Ejemplo:
5. Potencia de un cociente
En este caso las bases (a y b) son diferentes se dividen y elevados a un exponente (m), el resultado es que el exponente (m) multiplica con cada exponente de ambas bases. Observe la expresión de la sexta propiedad:
Ejemplo:
6. Potenciación de números enteros: Potencia de exponente cero (0)
En este caso toda base que esté elevada a la 0 (cero) siempre el resultado es 1 (uno), observe el siguiente ejemplo donde la base (a) representa la base.
a0 = 1
Ejemplo: 350 = 1
7. Potencia de exponente uno (1)
Cualquier número (base) que se encuentre elevado a la 1 el resultado siempre es el mismo valor inicial.
$$a^{1}=a$$
Ejemplo: 10451 = 1045
8. Potencia de exponente fraccionario
En este caso la base (a) tiene como exponente una fracción, al aplicarle la propiedad la base (a) queda como una cantidad subradical el numerador (m) queda como exponente entero de la base (a) y el denominador (n) pasa a ser el índice de la raíz. Observe la expresión de la octava propiedad:
Ejemplo:
9. Potencia de exponente negativo
Cuando la base (a) posee un exponente negativo (-m) la base (a) queda expresada en el denominador con el mismo denominador pero positivo (m)
Ejemplo:
Actividades de las propiedades de la potenciación de números enteros
I. Resuelva:
$$2^{3}.2^{2} = $$
$$5^{1}.5^{4}=$$
$$4^{2}.4^{3}=$$
- ¿Qué ocurre con los exponentes al multiplicar potencias con la misma base?
$$\frac{6^{4}}{6^{6}}=$$
$$\frac{10^{5}}{10^{3}}=$$
$$\frac{3^{6}}{3^{3}}=$$
- ¿Qué ocurre con los exponentes al dividir potencias con la misma base?
$$(-3^{3})^{4}=$$
$$(102^{3})^{0}=$$
$$(12^{2})^{2}=$$
- ¿Qué observas sobre los exponentes al aplicar la propiedad de la potencia de una potencia?
II. Aplicaciones de la potenciación de números enteros la vida cotidiana
➡ Calcula el volumen de las siguientes cajas usando la fórmula del volumen
$$V=l^{3}$$
- Una caja con lados de 3 cm.
- Una caja con lados de 5 cm.
- Una caja con lados de 7 cm.¿Cómo crece el volumen de una caja a medida que aumenta el tamaño del lado?
➡ Algunas bacterias se duplican cada hora, lo que significa que su crecimiento puede representarse con potencias de 2. Ejemplo: determinar las cantidades de bacterias después de 1, 2, 3, y 4 horas, sabiendo que:
1 hora: 21
2 horas 22 y así sucesivamente.
¿Cómo cambia la población de bacterias con cada hora que pasa? ¿Qué observas sobre el crecimiento?
➡ Investiga y representa en notación científica las siguientes distancias:
- Distancia de la Tierra al Sol: aproximadamente 149,600,000 km.
- Distancia de la Tierra a Marte: aproximadamente 225,000,000 km.
- Distancia de la Tierra a Júpiter: aproximadamente 778,000,000 km.
- ¿Por qué es útil usar potencias de 10 para representar estas distancias?
- ¿Cómo facilita esto la comparación entre diferentes distancias en el espacio?
Ahora que ya conoces las propiedades de la potenciación de números enteros es hora de poner manos a la obra, práctica cada uno de los casos y podrás mejorar tus habilidades con este contenido.
No olvides dejarnos tus comentarios, suscribirte y compartir nuestro contenido para seguir creciendo.
