
¿Alguna vez te has preguntado cómo los videojuegos logran que tus lanzamientos de granadas o tus tiros a distancia sean tan precisos?
Detrás de cada trayectoria perfecta en un videojuego, se esconde la matemática de los ángulos. Desde la precisión necesaria para un tiro en un simulador de francotirador hasta el ajuste del ángulo de un golpe de golf virtual, todo se basa en el sistema sexagesimal. Aprender a convertir y operar con grados, minutos y segundos no solo te hará mejor en geometría, sino que te dará una nueva perspectiva sobre la lógica que rige los mundos digitales que tanto nos gustan.
Medición de ángulos en el sistema sexagesimal
Al dividir una vuelta en 360 partes iguales, cada una de ellas tiene como medida un grado sexagesimal, es decir, la fracción 1/360 .
Si uno de dichos grados se divide en 60 partes iguales, cada una de las partes recibe el nombre de minuto. Es decir 1/60 de grado equivale a 1’, donde el símbolo ’ se lee minuto.
Al dividir cada minuto en 60 partes iguales, cada una de ellos recibe el nombre de segundo. Es decir, 1/60 de minuto equivale 1”, este símbolo se conoce como segundo.
Entonces, se concluye que: $$1^{\circ }=60’=3600^{\prime\prime}$$
Por lo tanto es muy importante que tengas siempre presente las siguientes relaciones:
$$1^{\circ }=60’$$
$$1^{\prime}=60^{\prime\prime}$$
$$1^{\circ }=3600^{\prime\prime}$$
Expresiones dentro del sistema sexagesimal
En el sistema sexagesimal, los ángulos pueden expresarse de dos maneras:
- Grados decimales.
- Grados, minutos y segundos.
Los grados decimales expresan una parte entera y otra decimal. Ejemplo: 62,35° y
Los grados sexagesimales tradicionales se representan en grados, minutos y segundos. Ejemplo: 62°21’0”
Transformación de grados decimales a grados, minutos y segundos
Transformar de grados decimales a grados, minutos y segundos es muy fácil, solo debes seguir el procedimiento paso a paso.
Ejemplo. Convertir 35,875° a grados, minutos y segundos.
Procedimiento
Primero. Igualar la medida del ángulo como la sumatoria de la parte entera y su parte decimal.
$$35,875^{\circ } = 35^{\circ } + 0,875^{\circ }$$
Segundo. Multiplicar la parte decimal por el factor \(\frac{60′}{1^{\circ }}\) para conseguir la cantidad de minutos.
$$35,875^{\circ } = 35^{\circ } + (0,875^{\circ } \cdot \frac{60′}{1^{\circ }})$$
$$35,875^{\circ } = 35^{\circ } + 52,5’$$
Si se obtiene una cantidad de minutos en decimales, nuevamente se expresa esa cantidad como la suma de su parte entera y su parte decimal multiplicándola por el factor \(\frac{60»}{1{‘}}\) .
$$35,875^{\circ } = 35^{\circ } + 52’+(0,5’\cdot \frac{60^{\prime\prime}}{1′})$$
$$35,875^{\circ } = 35^{\circ } + 52^{\prime}+30^{\prime\prime}$$
Finalmente, se concluye que la medida 35,875° = 35°52’30”.
Ejemplo. Expresar la medida del ángulo 15°12’25” en grados decimales.
Procedimiento
Primero. Descomponer la medida del ángulo como la suma de grados, minutos y segundos, convirtiendo cada uno en grados según su equivalencia.
$$15^{\circ }12^{\prime}25^{\prime\prime}=$$
Segundo. Realizar las operaciones indicadas, por lo que se obtiene:
$$15^{\circ }12^{\prime}25^{\prime\prime}= 15^{\circ } +0,2^{\circ }+0,006^{\circ }$$
$$15^{\circ }12^{\prime}25^{\prime\prime}= 15,206^{\circ }$$
Finalmente, se concluye que la medida angular 15°12’25” expresada en grados decimales es 15,206°.
Operaciones básicas
Las operaciones básicas en el sistema sexagesimal permiten sumar, restar, multiplicar y dividir ángulos expresados en grados, minutos y segundos. Para realizarlas correctamente, es necesario aplicar las siguientes equivalencias cuando superen su valor máximo.
$$1^{\circ }=60’$$
$$1^{\prime}=60^{\prime\prime}$$
$$1^{\circ }=3600^{\prime\prime}$$
Suma
Para poder llevar a cabo una suma de ángulos sexagesimales debes cumplir con los siguientes pasos:
- Ordenar ambos valores.
- Sumar.
- Si el resultado de los segundos es ≥ 60” o los minutos es ≥ de 60’ debes aplicar las equivalencias respectivas.
Caso # 1 : Cuando los minutos y segundos son menores que 60.
Ejemplo: Sume los ángulos α=15°12’25” y β = 12°21’10”
Ordene y sume.
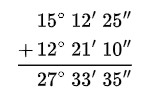
Explicación de suma de ángulos (video)
En este video de YouTube aprenderás cómo realizar la suma de ángulos sexagesimales paso a paso. Verás cómo se suman los grados, minutos y segundos de manera alineada, y qué hacer cuando los minutos o segundos superan los 60: transformarlos a la unidad superior. De esta forma comprenderás fácilmente cómo obtener el resultado correcto en el sistema sexagesimal.
Caso # 2 : Cuando los segundos son mayores o iguales a 60.
Este caso debes ordenar y sumar y si los segundos es mayor que 60” debes aplicar la equivalencia 1’ = 60”.
Ejemplo: Sume los siguientes ángulos α=49°24’32” y β = 63°21’42”
- Ordene y sume:

- Aplicar la relación 1´= 60´´
Como:
74´´= 60´´ + 14´´ . Se transforma 60´´ en 1´ , y queda 14´´.
Ese 1´ se suma con los 45´, dando 46´.
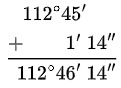
![]()
Caso # 3 : Cuando los minutos son mayores o iguales a 60.
Este caso debes ordenar y sumar y si los minutos es mayor que 60’ debes aplicar la equivalencia 1° = 60’ .
Ejemplo: Sume los siguientes ángulos α = 87°56’36” y β = 129°85’5”.
- Ordenar y sumar
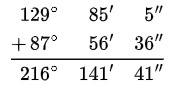
- Aplicar: 1° = 60´
Como 141´ = 60´ + 60´ +21´ . Se transforma 60´ +60´ = 120´ en 2° grado y quedan 21´.
Ese 2° se suma con los 216°, dando 218°.
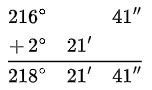
![]()
Caso # 4 : Cuando los minutos y segundos son menores o iguales a 60.
Este caso se realiza la equivalencia de segundos a minutos y luego de minutos a grados.
Ejemplo: Sume los siguientes ángulos α = 53°67’56” y β = 39°85’45”
- Ordenar y sumar
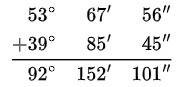
- Aplicar la equivalencia
Como 101´ ´= 60´´ + 41´´ . Se transforma y queda así: 1´ con 41´´.
Ese 1´ se suma con los 152´, dando 153´.
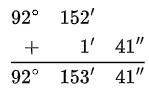
- Transformar los minutos a grados. 1°=60´
153´ = 60´ + 60´ + 33´´. Al transformarse la expresión es: 1° + 1° +33´
Esos 2° se suma a los 92°, resultando 94°.
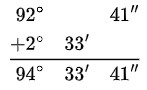
![]()
Resta
Para restar ángulos sexagesimales debes seguir estos pasos:
- Ordena ambos ángulos en columnas (grados, minutos y segundos).
- Realiza la resta correspondiente.
- Si el resultado de los segundos es ≥ 60” o los minutos es ≥ de 60’ aplica las equivalencias necesarias para convertirlos correctamente.
Caso # 1 : Cuando los minutos y segundos son menores que 60.
Ejemplo: Reste los ángulos 32°45’52” y 15°32’43”
- Ordenar y restar
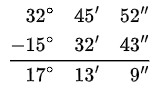
Caso # 2: Cuando el valor del ángulo menor posee segundos más elevados.
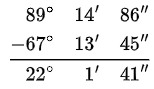
Ejemplo: Reste los ángulos 89°15´26´´y 67°13´45´´
- Ordenar. Observa que los segundos del ángulo menor es mayor que los segundos del ángulo mayor.

- Se le resta 1 minuto al mayor ángulo 89°15’26”, ese minuto se transforma a segundos y luego se suma a los 26 segundos. El fin de este procedimiento es lograr que los segundos sea mayor que los segundos del ángulo menor. Observa ahora:

- Reste:
Explicación de resta de ángulos (video)
En este video de YouTube aprenderás a realizar la resta de ángulos sexagesimales de forma sencilla. Te mostraré cómo restar grados, minutos y segundos en columnas y qué hacer cuando no es posible restar directamente: pedir prestado un grado y convertirlo en 60 minutos, o un minuto y transformarlo en 60 segundos. Así, paso a paso, lograrás obtener el resultado correcto dentro del sistema sexagesimal.
Caso # 3: Cuando la cifra mayor no posee minutos y segundos.
Ejemplo: Reste los ángulos 45° y 33° 45´34´´
- Ordenar:
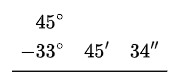
- Cuando un ángulo no presenta minutos ni segundos, se le resta 1° al valor de los grados. Ese grado se convierte en 60′. Luego, de esos 60′ se toma 1′ y se transforma en 60″ (1′ = 60″). De esta manera, el ángulo queda expresado con minutos y segundos suficientes para efectuar la resta. Observa:
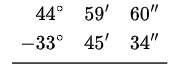
- Restar

Multiplicación
La multiplicación de ángulos sexagesimales se aplica cuando un ángulo debe repetirse varias veces, lo que equivale a multiplicarlo por un número entero o decimal. El procedimiento consiste en multiplicar el ángulo completo y expresar el resultado en grados, minutos y segundos. Según el caso, si los minutos y segundos obtenidos son menores que 60, se dejan como están; pero si son iguales o mayores que 60, se convierten a la unidad superior correspondiente.
Caso # 1: Cuando en el resultado los minutos y los segundos son menores que 60
Ejemplo: Multiplicar 4 y 4° 12’9”
- Ordenar y multiplicar
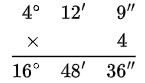
Caso # 2: Cuando en el resultado los minutos o los segundos son mayores o iguales a 60
Ejemplo: Multiplicar 15 y 3°12’14”
- Ordenar y multiplicar
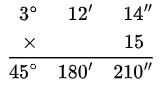
- Transformar los segundos y minutos que están fuera de su rango normal (≥ 60″ o ≥ 60′) a su equivalente en minutos y grados respectivamente, para expresar el ángulo de forma correcta.
210´´ =60´´ + 60´´ + 60´´ + 30´´ = 3´ + 30´´
3´ + 180´ = 183´
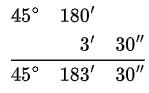
- Transformar los minutos a grados.
183´ = 60´ + 60´ + 60´ + 3´ = 3° + 3´
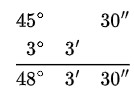
Observa que los minutos y segundos están por debajo de los 60.
División
La división de ángulos en el sistema sexagesimal consiste en repartir un ángulo dado en partes iguales. El procedimiento consiste en dividir entre el número indicado y, finalmente, transformar la parte decimal del resultado en minutos y segundos.
Ejemplo: Divida 42° 36´ 56´´ entre 4
- Dividir
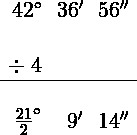
- Transformación de grados decimales a minutos.
21°/2 = 10,5°
$$10,5^{\circ } = 10^{\circ } + 0,5^{\circ }$$
$$10,5^{\circ } = 10^{\circ } + (0,5^{\circ } \cdot \frac{60^{\prime}}{1^{\circ }})$$
$$10,5^{\circ } = 10^{\circ } + 30^{\prime}$$
$$10,5^{\circ } = 10^{\circ } 30^{\prime}$$
- Sumar los minutos y segundos resultantes

Resultado: 10°39’14”.
Ejemplo: Divida 156° 26´ entre 8
- Ordenar y dividir

- Transformación de grados decimales a minutos.
$$19,5^{\circ } = 19^{\circ } + 0,5^{\circ }$$
$$19,5^{\circ } = 19^{\circ } + (0,5^{\circ } \cdot \frac{60^{\prime}}{1^{\circ }})$$
$$19,5^{\circ } = 19^{\circ } + 30^{\prime}$$
- Sumar los 30 minutos.

- Transformación de minutos decimales a segundos
$$33.25^{\prime } = 33^{\prime}+0,25^{\prime }$$
$$33.25^{\prime } = 33^{\prime} + (0,25^{\prime} \cdot \frac{60^{\prime\prime}}{1^{\prime }})$$
$$63.35^{\prime } = 33^{\prime}+ 15^{\prime\prime}$$
- Sumar los minutos y segundos.
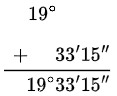
Resultado: 19°33’15”.
Actividades
Exprese cada ángulo decimales en grados, minutos y segundos sexagesimales.
| a. | 0,629° | e. | 38,20° | i. | 8,952° |
| b. | 15,289° | f. | 60,728° | j. | 45,235° |
| c. | 0,4791° | g. | 49,371° | k. | 119,35° |
| d. | 60,589° | h. | 89,99° | l. | 179,50° |
Resuelva las siguientes operaciones.
45°3´56´´ + 69°25´36´´
45°3´56´´ – 69°25´36´´
45 x 69°25´36´´
5°3´6´´ + 4°
Diga si es verdadero o falso los siguientes planteamientos.
- 60° es equivalente a 36000´´
- El resultado de 3°65´98´´ + 1°3´9´´ es 5°9°46´´
- Pedro afirma que 1° = 60´ = 3600´´
Dos tubos de una estructura forma un ángulo de 52°17´33´´. La medida en grados de dicho ángulo es:
- 52,85°
- 53,34°
- 52,29°
- 53,17°
