Comprender las conversiones de unidades brinda la posibilidad de poder comparar y conocer diferentes medidas no solo en la ciencia sino también en la vida diaria. ¿Sabías que un guepardo puede llegar alcanzar una velocidad de 120km/h comparable a la de un vehículo?. Sin embargo, puede ocurrir una variedad de situaciones donde se requiera efectuar cálculos científicos o un análisis se seguridad vial, haciendo uso de otras unidades como metros por segundos (m/s). Su finalidad es adaptar esa velocidad a distintos contextos.
Comprender las conversiones de unidades brinda la posibilidad de poder comparar y conocer diferentes medidas no solo en la ciencia sino también en la vida diaria. ¿Sabías que un guepardo puede llegar alcanzar una velocidad de 120km/h comparable a la de un vehículo?. Sin embargo, puede ocurrir una variedad de situaciones donde se requiera efectuar cálculos científicos o un análisis se seguridad vial, haciendo uso de otras unidades como metros por segundos (m/s). Su finalidad es adaptar esa velocidad a distintos contextos.
Las conversiones de unidades se da cuando cambias de una moneda a otra, por ejemplo de dólar a euros, o de litros a galones, de kilogramos a toneladas, pulgadas a milímetros. Convertir unidades te ayuda a resolver problemas en matemáticas, física, química y hasta en tu diario vivir.
Definición de conversiones de unidades
| Se refiere a un cambio de unidades pertenecientes a una misma magnitud. |
Sistema Internacional de medidas S.I.
 Es el sistema estándar más utilizado a nivel mundial, fue establecido en el año 1960 por la Conferencia General de Pesas y Medidas (CGPM). Basado en el sistema métrico introducido por Francia en 1795.
Es el sistema estándar más utilizado a nivel mundial, fue establecido en el año 1960 por la Conferencia General de Pesas y Medidas (CGPM). Basado en el sistema métrico introducido por Francia en 1795.
El Sistema Internacional (S.I.) hace uso de prefijos para expresar magnitudes a distintas escalas, desde las más pequeñas hasta las más grandes. Permitiendo simplificar y adaptar las medidas a distintas exigencias.
Prefijos del S.I.
El S.I. posee una gran variedad de prefijos y se aplica a las unidades de cada magnitud física. La razones para su utilización se debe a:
1. Permitir la expresión de valores muy grandes o muy pequeños a cifras compactadas y comprensibles.
2. Facilita la lectura de números con muchos ceros, manteniendo su precisión.
3. Se hace más fácil captar el valor y comunicar las medidas.
Cada magnitud física posee una unidad principal, esta unidad no debe poseer prefijo con la intención de poder combinarla con cada prefijo del S.I. quedando finalmente una variedad de unidades perteneciente a esa magnitud física.
Cabe destacar que en unidades de magnitudes de temperatura (Kelvin “K”), cantidad de sustancia (Mol “mol”) e intensidad lumínica (Candela “cd”) no se aplica la combinación con los prefijos ya que no es practico en la realidad.
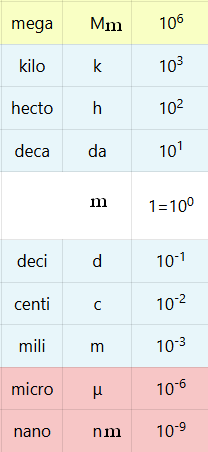
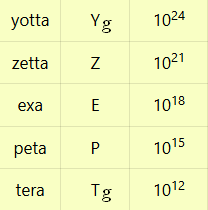
Tabla de prefijos del S.I.
En la tabla de prefijos podrás observar:
1. Posición (posición).
2. Prefijo.
3. Símbolo.
4. Orden de magnitud o factor.
Nota
La posición (P) se utiliza para identificar qué prefijos tienen un valor mayor que otros.
| P | Prefijo | Símbolo | Orden de magnitud | |
| 1 | yotta | Y | 1024 | M |
| 2 | zetta | Z | 1021 | |
| 3 | exa | E | 1018 | |
| 4 | peta | P | 1015 | |
| 5 | tera | T | 1012 | |
| 6 | giga | G | 109 | |
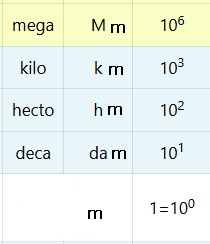
| 7 | mega | M | 106 | |
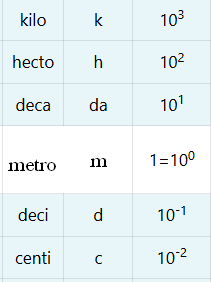
| 8 | kilo | k | 103 | |
| 9 | hecto | h | 102 | |
| 10 | deca | da | 101 | |
| 11 | Unidad sin prefijo | 1=100 | ||
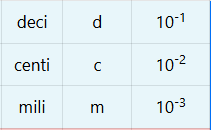
| 12 | deci | d | 10-1 | S u b m u l t i p l o s |
| 13 | centi | c | 10-2 | |
| 14 | mili | m | 10-3 | |
| 15 | micro | μ | 10-6 | |
| 16 | nano | n | 10-9 | |
| 17 | pico | p | 10-12 | |
| 18 | femto | f | 10-15 | |
| 19 | atto | a | 10-18 | |
| 20 | zepto | z | 10-21 | |
| 21 | yocto | y | 10-24 | |
Combinaciones de las unidades con prefijos S.I.
Es muy fácil realizar las combinaciones, solo debes tener la unidad sin prefijo de la magnitud física.
Combinaciones con la unidad de longitud
Para la magnitud longitud su unidad es el metro (m), la combinación queda expresada de la siguiente manera:
| Longitud | ||
| Prefijo | Símbolo | Combinación |
| yotta | Y | Ym |
| zetta | Z | Zm |
| exa | E | Em |
| peta | P | Pm |
| tera | T | Tm |
| giga | G | Gm |
| mega | M | Mm |
| kilo | k | km |
| hecto | h | hm |
| deca | da | dam |
| Unidad sin prefijo | m | |
| deci | d | dm |
| centi | c | cm |
| mili | m | mm |
| micro | μ | μm |
| nano | n | nm |
| pico | p | pm |
| femto | f | fm |
| atto | a | am |
| zepto | z | zm |
| yocto | y | ym |
La lectura de cada uno de ellos es mencionar el nombre del prefijo con tilde en la segunda sílaba + la unidad. Ejemplo:
Yottámetro (Ym); zettámetro (Zm); kilómetro (km); micrómetro (μm); nanómetro (nm); centímetro (cm); milímetro (mm); megámetro (Mm); Petámetro (Pm).
Combinaciones con la unidad de masa
Para la magnitud masa, la unidad principal es el kilogramo (kg). Pero como esta unidad posee prefijo la unidad usada para la combinación es el gramo (g). Entonces la combinación queda de la siguiente forma:
| Masa | ||
| Prefijo | Símbolo | Combinación |
| yotta | Y | Yg |
| zetta | Z | Zg |
| exa | E | Eg |
| peta | P | Pg |
| tera | T | Tg |
| giga | G | Gg |
| mega | M | Mg |
| kilo | k | kg |
| hecto | h | hg |
| deca | da | dag |
| Unidad sin prefijo | g | |
| deci | d | dg |
| centi | c | cg |
| mili | m | mg |
| micro | μ | μg |
| nano | n | ng |
| pico | p | pg |
| femto | f | fg |
| atto | a | ag |
| zepto | z | zg |
| yocto | y | yg |
Cómo pudiste notar es fácil realizar estas combinaciones, así como se hizo con estas dos magnitudes las puedes hacer también con otras como la de capacidad, volumen, área, tiempo, velocidad, aceleración, entre otras.
¿Cómo debo hacer las conversiones?
 Cuando se realiza una conversión siempre va existir dos unidades, una de partida y la otra de destino.
Cuando se realiza una conversión siempre va existir dos unidades, una de partida y la otra de destino.
La unidad de partida es la que se cambia, mientras que la unidad de destino es como finalmente se expresa una medida.
Por ejemplo: Convertir 5 km → m.
Unidad de partida = km y la unidad de destino = m.
Para poder hacer cualquier conversión debes cumplir con los siguientes pasos:
I.Identificar la unidad con mayor y menor orden de magnitud. Ver tabla # 1.
II.Dividir la orden de magnitud mayor entre la menor.
III.Construir el factor de conversión entre las dos unidades: se asigna el valor de 1 a la unidad de mayor orden de magnitud y se iguala al cociente obtenido en el paso anterior.
IV.Multiplicar el valor de la unidad de partida por el factor de conversión obtenido en el paso 3, expresado en forma de fracción para permitir la cancelación de la unidad inicial.
Ejercicios de conversiones de unidades de longitud
 Cada ejemplo se muestran con explicaciones paso a paso.
Cada ejemplo se muestran con explicaciones paso a paso.
Usa la tabla de prefijos del S.I. y comprobarás lo fácil que es convertir cualquier unidad de longitud.
Si deseas comprobar los resultados de forma rápida y segura puedes usar EduConvert
Dale clic allí ➡️ Ir a EduConvert
Ejemplo # 1: Convertir 10m → dm
Solución
 Unidad de partida = m Unidad de destino = dm
Unidad de partida = m Unidad de destino = dm
Primero. La unidad con mayor orden de magnitud es el metro.
Segundo. Dividir.$$\frac{10^{0}}{10^{-1}}=10^{1}$$
Tercero. Construcción del factor de conversión.$$1m=10^{1}dm$$
Cuarto. Multiplicar la magnitud dada con su factor de conversión construido.
![]()
$$\boxed{10m=100dm}$$
Ejemplo # 2: Convertir 8km → cm
Solución
 Unidad de partida = km Unidad de destino = cm
Unidad de partida = km Unidad de destino = cm
Uno. La unidad de mayor orden de magnitud es el kilómetro.
Dos. Dividir.$$\frac{10^{3}}{10^{-2}}=10^{5}$$
Tres. Crea el factor de conversión.$$1km=10^{5}cm$$
Cuarto. Multiplicar la magnitud dada con el factor de conversión.
![]()
Ejemplo # 3: Convertir 1500mm → dm
Solución
 Unidad de partida = mm Unidad de destino = dm
Unidad de partida = mm Unidad de destino = dm
- La unidad de mayor orden de magnitud es el decímetro.
- Dividir.$$\frac{10^{-1}}{10^{-3}}=10^{2}$$
- Factor de conversión.$$1dm=10^{2}mm$$
- Multiplicar.
![]()
Ejemplo # 4: Convertir 23Mm → m
Solución
 Unidad de partida = Mm Unidad de destino = m
Unidad de partida = Mm Unidad de destino = m
- Unidad de mayor orden de magnitud es el Megámetro.
- Dividir. $$\frac{10^{6}}{10^{0}}=10^{6}$$
- Factor de conversión.$$1Mm=10^{6}m$$
- Eliminar la unidad de partida.
![]()
En notación científica:$$=2,3\cdot 10^{1}\cdot 10^{6}m=2,3\cdot 10^{7}m$$
Ejemplo # 5: Convertir 105 000 nm → Mm
Solución
Se expresa 105 000 nm en notación científica quedando de la siguiente forma:
1,05.105nm
Unidad de partida = Mm Unidad de destino = nm
- La unidad de mayor orden de magnitud es el Megámetro.
- Dividir. $$\frac{10^{6}}{10^{-9}}=10^{15}$$
- Factor de conversión.$$1Mm=10^{15}nm$$
- Resultado.
![]()
$$=1,05\cdot 10^{-10}Mm$$
Conversiones de unidades de masa
El procedimiento es idéntico al de las unidades de longitud, la diferencia es que debes poseer la tabla de todos los prefijos para la magnitud de masa.
Dale clic allí ➡️ Ir a EduConvert y realiza conversiones de masa.
Ejemplo # 1: Convertir 36 Yg → Tg
Solución
 Unidad de partida = Yg Unidad de destino = Tg
Unidad de partida = Yg Unidad de destino = Tg
- Unidad de mayor orden de magnitud es Yottagramo.
- Dividir. $$\frac{10^{24}}{10^{12}}=10^{12}$$
- Factor de conversión.$$1Yg=10^{12}Tg$$
- Eliminación de unidades.
![]()
![]()
Ejemplo # 2: Convertir 15 000 kg → T
Solución
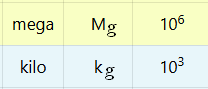 Unidad de partida = kg Unidad de destino = T (Tonelada)
Unidad de partida = kg Unidad de destino = T (Tonelada)
Observación: Tonelada se conoce también como Megagramo. Entonces: T=Mg
- La unidad de mayor orden de magnitud es el Megagramo.
- Dividir. $$\frac{10^{6}}{10^{3}}=10^{3}$$
- Factor de conversión.$$1Mg=10^{3}kg$$
- Eliminación de unidades de partida.
![]()
Conversiones de unidades del Sistema Internacional a otros sistemas y viceversa
Aquí la conversión resulta más sencilla, porque el factor de conversión no lo debes elaborar tú: ya está proporcionado.
Tabla de magnitudes: Longitud, masa, volumen, fuerza, presión, área y tiempo con su factor de conversión.
A continuación, la tabla:
| Magnitud | Unidad de otros sistemas | Factor de conversión |
| Longitud | Pulgada | 1 in = 2,54 cm |
| Pie | 1 ft = 30,48 cm | |
| Yarda | 1 yd = 0,914 m | |
| Milla | 1 mi = 1,609 km | |
| Masa | Libra | 1 lb = 453,6 g |
| Onza | 1 oz = 28,35 g | |
| Tonelada | 1 t = 1 000 kg | |
| Volumen | Galón | 1 gal = 3,785 L |
| Pie cúbico | 1 ft3 = 28,3168 L | |
| Metro cúbico | 1 m3 = 1 000L | |
| Fuerza | Kilogramo-fuerza | 1 kgf = 9,80665 N |
| Kilopondio | 1kp = 9,80665 N | |
| Dina | 1 dyn = 10-5 N | |
| Libra-fuerza | 1lbf = 4,44822 N | |
| Presión | Bar | 1bar = 100 000 Pa |
| Kilopascal | 1 kPa = 1 000 Pa 1kPa = 1 000N/m2 | |
| Libra por pulgada cuadrada | 1 psi = 6 894,76 Pa | |
| Área | Acre | 1 ac = 4 046,86 m2 |
| Yarda cuadrada | 1 yd2 = 0,836127 m2 | |
| Tiempo | Minuto | 1 min = 60 s |
| Hora | 1 h = 60 min | |
| Hora | 1 h = 3600 s | |
| Día | 1 d = 24 h | |
| Mes | 1 mes = 2 629 746 s | |
| Mes | 1 mes =43 824 min | |
| Mes | 1 mes ≈ 30,44 días | |
| Semana | 1 semana = 604 800 s | |
| Semana | 1 semana = 7 días | |
| Quincena | 1 quincena = 15 días | |
| Trimestre | 1 trimestre = 3 meses | |
| Año | 1 año ≈ 365,25 días | |
| Bimestre | 1 bimestre = 2 meses | |
| Semestre | 1 semestre = 6 meses | |
| Bienio | 1 bienio = 2 años | |
| Trienio | 1 trienio = 3 años | |
| Cuatrienio | 1 cuatrienio = 4 años | |
| Lustro | 1 lustro = 5 años | |
| Década | 1 década = 10 años |
Dale clic allí ➡️ Ir a EduConvert y conviertes fácil y rápido.
Ejemplo # 1: Convertir 3 in → cm
Solución
![]()
Ejemplo # 2: Convertir 4530 km → mi
Solución
![]()
Conversiones de unidades de velocidad
Las unidades de velocidad son unidades derivadas, compuesta por magnitudes de longitud y tiempo. Si la exigencia es transformar ambas unidades se crea 2 factores de conversión, pero todo depende de la situación porque puede presentarse con más de dos factores.
Dale clic allí ➡️ Ir a EduConvert y realiza conversiones de velocidad.
Ejemplo # 1: Convertir 3 m/s → cm/min
Solución
 Unidad de partida = m/s Unidad de destino = cm/min
Unidad de partida = m/s Unidad de destino = cm/min
Observación: Tanto las unidades de longitud y tiempo deben ser transformadas por lo tanto se debe crear 2 factores de conversión.
- La unidad de mayor orden de magnitud es el metro.
- Dividir. $$\frac{10^{0}}{10^{-2}}=10^{2}$$
- Factores de conversión.$$1m=10^{2}cm$$
$$1min=60s$$ - Multiplicar para eliminar las unidades dadas.
![]()
![]()
- En notación científica:
![]()
Ejemplo # 2: Convertir 10 dam/h → hm/μs
Solución
 Unidad de partida = dam/h Unidad de destino = hm/μs
Unidad de partida = dam/h Unidad de destino = hm/μs
Observación: En esta situación debe crearse 3 factores de conversión. El primero es para la longitud, el segundo de horas a segundo y el tercero de segundos a microsegundos.
- La unidad de longitud de mayor orden de magnitud es el hectómetro.
- Dividir.$$\frac{10^{2}}{10^{1}}=10^{1}$$
- Factores de conversión.
Longitud
1hm = 101dam
Tiempo
1h = 3600 s (tabla # 2)
1s = 10-6μs (tabla # 1)
- Multiplicar los tres factores.
![]()
- En notación científica:
![]()
Conversiones de unidades de aceleración
 El procedimiento es similar a las conversiones de unidades de velocidad, con la diferencia que el factor tiempo debe elevarse al cuadrado.
El procedimiento es similar a las conversiones de unidades de velocidad, con la diferencia que el factor tiempo debe elevarse al cuadrado.
Dale clic allí ➡️ Ir a EduConvert y realiza conversiones de aceleración.
Ejemplo # 1: Convertir 20 m/s2 → m/h2
Solución
Unidad de partida = m/s2 Unidad de destino = m/h2
Observación: La única unidad que se debe transforma es la de tiempo.
- Factor de conversión
Tiempo
1h = 3600 s (tabla # 2)
- Multiplicar
![]()
![]()
![]()
![]()
- En notación científica:
![]()
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
I. Convierta y exprese los resultados en notación científica.
- 0,000097.10-36 am → m
- 99,7.1015 Gm → dm
- 33,9.10-9 mg → kg
- 993,9.1012 T → kg
- 3 110,4.1052 s → meses
- 2 000 000 ps → semanas
- 432 000 km/h → m/s
- 97,64 cm/min → hm/s
II. Van tres personas caminando y un encuestador le pregunta: ¿Cuánto tiempo tardan desde sus casas a la iglesia? las tres personas responden respectivamente: un cuarto de hora, 7500s y 96min.
¿Qué persona llega de segunda y tercera a la iglesia?
III. La masa de un planeta es de 90718.1025mg ¿Cuál es la masa del planeta en libras?
IV. El diámetro de la rueda de una bicicleta es de 571,5mm ¿Cuánto es el diámetro en pulgadas (in)?
V. Un carro va con una velocidad de 97000dm/h. ¿Cuánto sería la velocidad expresada en m/s?
VI. La altura de un obrero es de 1,52m. Exprese su altura en pies (ft)
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión