 ¿Te has preguntado alguna vez qué tiene que ver la parábola con cosas que ves todos los días?
¿Te has preguntado alguna vez qué tiene que ver la parábola con cosas que ves todos los días?
Piensa en el chorro de agua que sale de una botella cuando la aprietas, en la trayectoria que hace un balón cuando lo pateas con un buen efecto, o en la forma curva de una lámpara que refleja la luz justo donde la necesitas. Aunque no lo notes, todas esas situaciones comparten la misma figura matemática.
Esa curva tan característica —suave, simétrica y fácil de reconocer— es la parábola. Conocerla te ayudará no solo en tus clases, sino también a entender por qué muchos objetos, diseños y movimientos del día a día tienen esa forma tan particular.
¿Qué es la parábola?
La parábola es el lugar geométrico de los puntos de un plano que mantienen la misma distancia a un punto fijo llamado foco (F) y de una recta fija denominada directriz.
En otras palabras la parábola es una curva cónica definida por la igualdad de distancia entre un punto fijo llamado foco (F) y una recta fija (directriz). Observa la imagen:
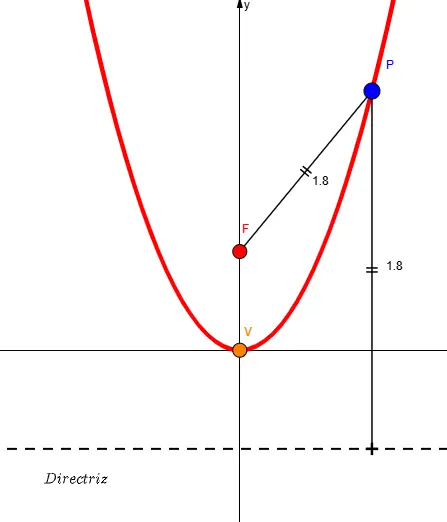
¿Es importante aprenderse la definición?
Si, cuando comprendes que cada punto de la parábola está a la misma distancia del foco y de la directriz, empiezas a ver que la curva no es un dibujo caprichoso: responde a una regla geométrica muy precisa. Esa idea te permite interpretar las ecuaciones, identificar una parábola en cualquier forma y resolver problemas con más seguridad, es decir ayuda a darle sentido geométrico y cuando comprendes el sentido los procedimientos dejan de ser complicados y comienza a tener lógica.
Compruébalo tú mismo la definición con este simulador interactivo
Mueve el punto P a lo largo de la curva y observa cómo siempre se mantiene la misma distancia al foco y a la directriz.
Es una forma sencilla y visual de entender que la definición no es solo teoría: realmente se cumple en cada punto de la curva. Mueve el punto y experimenta por ti mismo.
¿Para qué sirven las parábolas en la vida real?
La parábola aparece más seguido de lo que piensas. La ves en la forma de un reflector que concentra la luz en un punto, en las antenas parabólicas que reciben señales, en puentes colgantes, en chorros de agua, en la trayectoria de un balón e incluso en el diseño de lámparas o micrófonos.
Lo bonito es que entender la parábola no solo te sirve para resolver ejercicios: te ayuda a explicar por qué algunos objetos y movimientos del mundo funcionan de manera tan precisa.
¿Cómo puedes saber si una ecuación representa una parábola o no?
La pista más fácil es fijarte en los términos cuadrados.
- Si aparece solo un término cuadrado, por ejemplo:$$x^{2}\;\;o\;\;y^{2}$$ entonces es una parábola.
- Si aparecen dos términos cuadrados, ya puede ser una circunferencia, una elipse o una hipérbola, dependiendo de cómo estén.
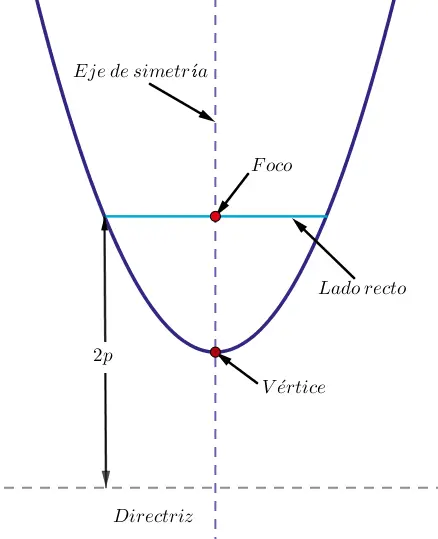
Elementos de la parábola
En la definición conociste dos elementos muy relevantes como la directriz y el foco, aquí nuevamente los mencionaré agregándole otras más.
 1. Foco
1. Foco
Es un punto fijo donde equidistan todos los puntos de la parábola.
2. Directriz
Es una recta fija respecto a la cual se mide la distancia de los puntos de la parábola.
3. Eje de simetría o eje focal
Es la recta que pasa por el foco y el vértice, partiendo en dos partes iguales a la parábola.
4. Vértice
Es un punto de intersección entre la parábola y el eje de simetría.
5. Lado recto
Es un segmento que pasa por el foco y cuyos dos extremos están sobre la curva cónica. Siempre es perpendicular al eje de simetría, formándose como una especia de puente que cruza la parábola.
Se calcula aplicando la siguiente expresión:$$Lr=|4\cdot p|$$
6. Parámetro
El parámetro de la curva cónica (2p) es la distancia del foco (F) a la directriz.
El semiparámetro es la distancia del foco al vértice denominado p y la distancia del vértice a la directriz también es p, es decir, que son las mismas distancias. Al sumarlas genera el parámetro de la parábola (2p)
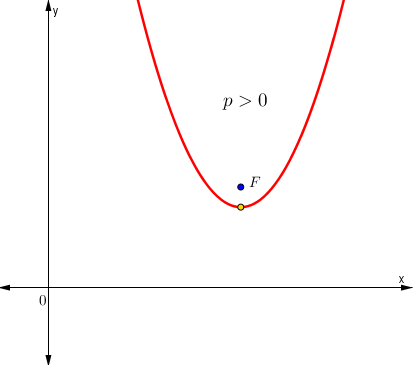
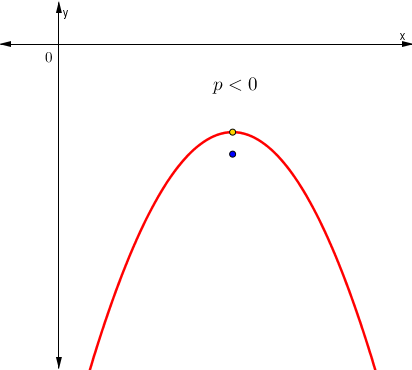
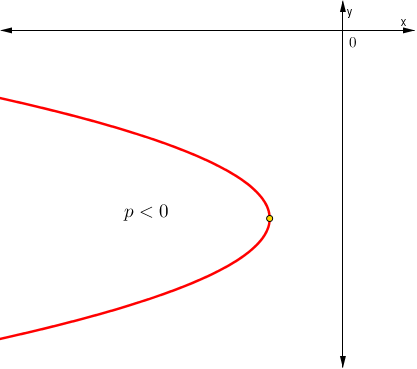
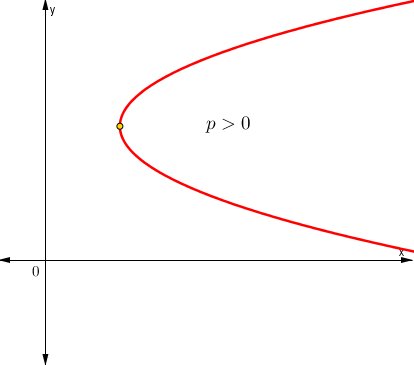
Características relevantes del parámetro cuando la parábola posee eje de simetría vertical:
- Sí p > 0 La parábola es cóncava hacia arriba.
- Sí p < 0 La parábola es cóncava hacia abajo.
Características relevantes del parámetro cuando la parábola posee eje de simetría horizontal:
- Sí p > 0 La parábola abre a la derecha.
- Sí p < 0 La parábola abre a izquierda.
Ecuación canónica con vértice en (0,0) y eje vertical
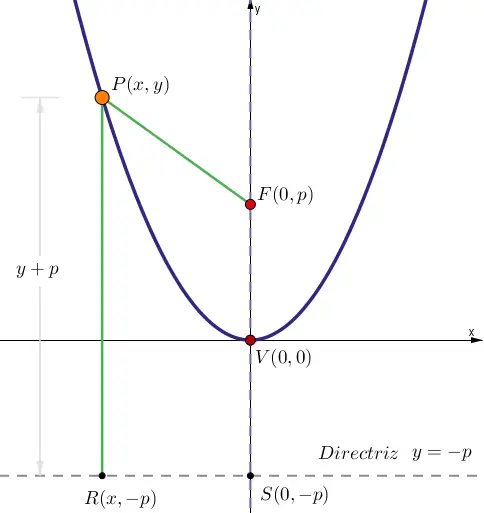 La figura muestra una parábola con vértice en el origen del plano cartesiano y con eje de simetría en el eje «y». para obtener la ecuación canónica debes aplicar la definición:
La figura muestra una parábola con vértice en el origen del plano cartesiano y con eje de simetría en el eje «y». para obtener la ecuación canónica debes aplicar la definición:
1. Distancia entre los puntos P(x,y) y F(p,0)
$$\overline{PF}=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$$
Reemplazar los valores:
$$\overline{PF}=\sqrt{(x-0)^{2}+(y-p)^{2}}$$
2. Distancia entre el P(x,y) a la directriz: y=-p
$$\overline{PR}=\frac{\left | Ax+By+C\right |}{\sqrt{A^{2}+B^{2}}}$$
Sustituir el punto P y la recta: y + p = 0
$$\overline{PR}=y+p$$
3. Aplicar la definición:$$\overline{PF}=\overline{PR}$$
$$\sqrt{(x-0)^{2}+(y-p)^{2}}=y+p$$
Elevar al cuadrado ambos miembros de la ecuación para eliminar la raíz cuadrada:
$$\left (\sqrt{x^{2}+y^{2}-2py+p^{2}} \right )^{2}=(y+p)^{2}$$
$$x^{2}+y^{2}-2py+p^{2}=y^{2}+2py+p^{2}$$
$$x^{2}+\not y^{2}-\not y^{2}-2py-2py+\not p^{2}-\not p^{2}=0$$
Ecuación de la parábola:
$$x^{2}-4py=0$$
Ecuación canónica:
$$x^{2}=4py$$
| $$x^{2}=4py$$ | |
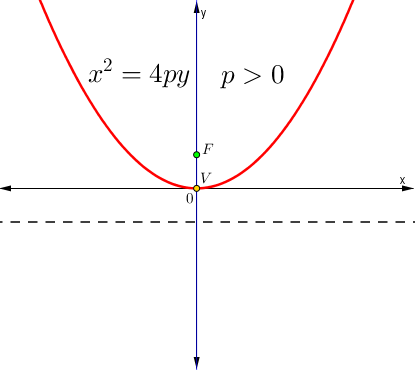 | 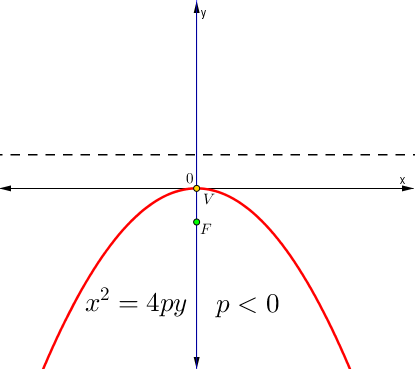 |
Foco y directriz
| Foco | Directriz |
| $$F(0,p)$$ | $$y+p=0$$ |
Ecuación canónica con vértice en (0,0) y eje horizontal
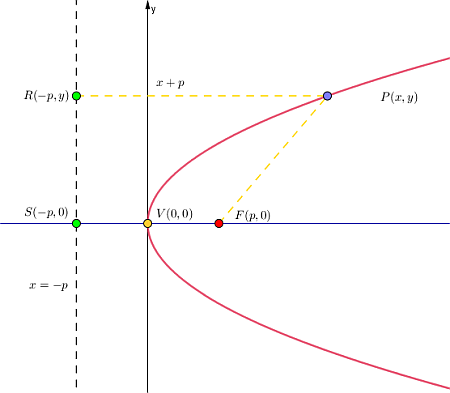 La figura muestra una parábola con vértice en (0,0) y con eje de simetría en el eje x, para obtener la ecuación canónica también debes aplicar también su definición:
La figura muestra una parábola con vértice en (0,0) y con eje de simetría en el eje x, para obtener la ecuación canónica también debes aplicar también su definición:
1. Distancia entre el punto P(x,y) y F(p,0).
$$\sqrt{(x-p)^{2}+(y-0)^{2}}$$
2. Ecuación de la directriz.
$$x+p=0$$
3. Distancia entre el punto P(x,y) a la directriz.
$$\overline{PR}=\frac{\left | Ax+By+C\right |}{\sqrt{A^{2}+B^{2}}}$$
Sustituir valores:
$$\frac{\left | x+p\right |}{\sqrt{1+0}}=x+p$$
4. Aplicar la definición de la parábola
$$\overline{PF}=\overline{PR}$$
Sustituyendo queda así:
$$\sqrt{(x-p)^{2}+(y-0)^{2}}=x+p$$
$$\left ( \sqrt{x^{2}-2px+p^{2}+y^{2}} \right )^{2}=(x+p)^{2}$$
$$x^{2}-2px+p^{2}+y^{2}=x^{2}+2px+p^{2}$$
$$\not x^{2}-2px+\not p^{2}+y^{2}-\not x^{2}-2px-\not p^{2}=0$$
Ecuación de la parábola:
$$y^{2}-4px=0$$
Ecuación canónica:
$$y^{2}=4px$$
| $$y^{2}=4px$$ | |
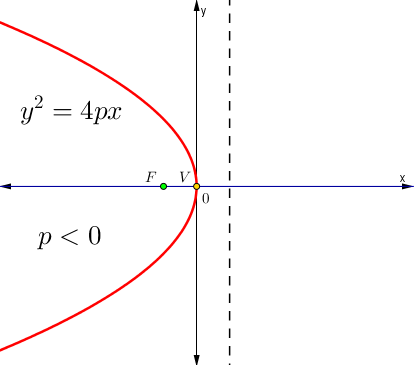 | 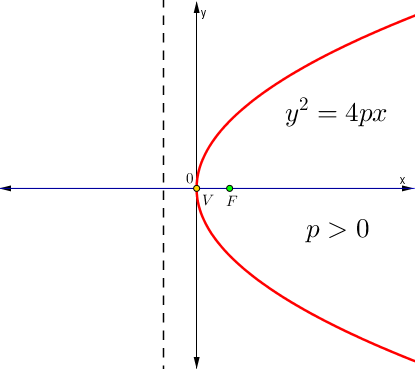 |
Foco y directriz
| Foco | Directriz |
| $$F(p,0)$$ | $$x+p=0$$ |
Ecuación canónica con vértice en (h,k) y eje de simetría paralelo al eje y
Para encontrar la ecuación canónica de una parábola con vértice (h,k) es conveniente efectuar una traslación de ejes, observa la imagen:
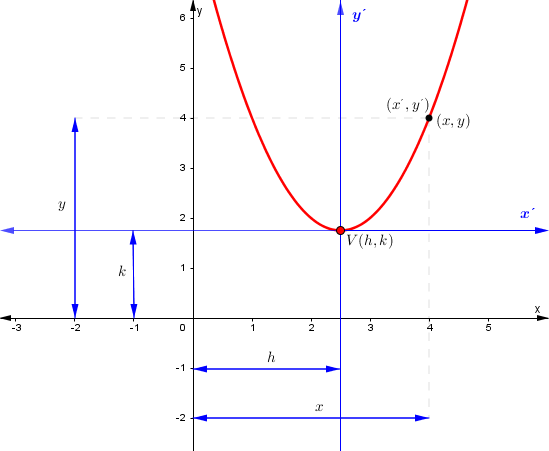
Esto es como trasladar la curva desde el origen del plano cartesiano a la posición (h, k). Quedando el sistema de coordenadas como x´- y´ y la ecuación de la misma así:$$x^{\prime 2} = 4p\,y^{\prime}$$
Luego:
$$x=x^{\prime }+h$$
$$y=y^{\prime}+k$$
Se tiene que:
$$x^{\prime}=x-h$$
$$y^{\prime}=y-k$$
Ecuación canónica:
$$(x-h)^{2}=4p(y-k)$$
| $$(x-h)^{2}=4p(y-k)$$ | |
 |  |
Elementos
| Vértice | $$(h,k)$$ |
| Ecuación de la directriz | $$y=k-p$$ |
| Foco | $$F(h,k+p)$$ |
| Ecuación del eje de simetría | $$x=h$$ |
Explora la Parábola: mueve el vértice, cambia el foco y domina su ecuación
¿Quieres entender realmente qué es una parábola sin memorizar largas definiciones?
En este simulador interactivo podrás mover el vértice (h,k), modificar el parámetro p ver cómo cambia el foco, la directriz y hasta la ecuación de la parábola… ¡todo en tiempo real!
Es una forma visual, dinámica y súper intuitiva de comprender cómo cada elemento afecta la forma y posición de la parábola. Solo arrastra, observa y deja que la gráfica te hable.
Ecuación canónica con vértice en (h,k) y eje de simetría paralelo al eje x
Para encontrar la ecuación canónica se trabaja de la misma manera como cuando su eje de simetría es paralelo al eje y.
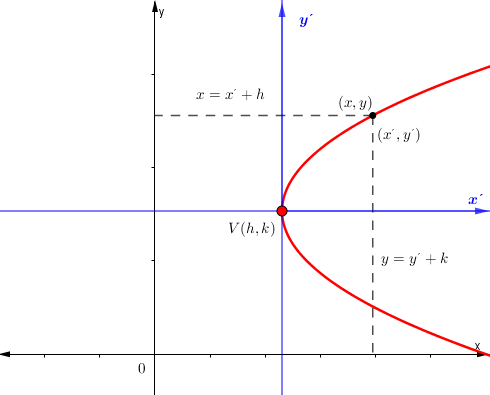
Sistema de coordenadas: x´- y´
Ecuación:$$y^{\prime 2} = 4p\,x^{\prime}$$
Luego:
$$x=x^{\prime }+h$$
$$y=y^{\prime}+k$$
Se tiene:
$$x^{\prime}=x-h$$
$$y^{\prime}=y-k$$
Ecuación canónica:
$$(y-k)^{2}=4p(x-h)$$
| $$(y-k)^{2}=4p(x-h)$$ | |
 |  |
Elementos
| Vértice | $$V(h,k)$$ |
| Ecuación de la directriz | $$x=h-p$$ |
| Foco | $$F(h+p,k)$$ |
| Eje de simetría | $$y=k$$ |
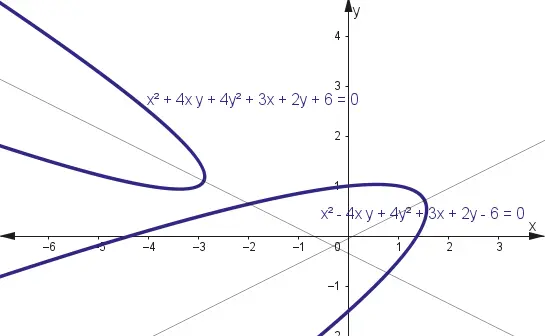
Ecuación general de la parábola
La ecuación general de la parábola es:
$$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$$
Esta ecuación incluye todas las parábolas como las cóncavas hacia arriba, cócavas hacia abajo, abiertas a la derecha, abiertas a la izquierda e incluso las que poseen ejes de simetría oblicuas o inclinadas. Observa la siguiente imagen de parábolas con ejes inclinados:
Características resaltantes
1. Cuando el término xy (B=0) no existe es porque la curva cónica posee eje de simetría vertical o horizontal la orientación depende de los coeficientes A y C. Observa la tabla:
| Coeficientes | $$A\neq 0\;\; y\;\; C=0$$ | $$C\neq 0\;\; y\;\; A=0$$ |
| Término cuadrático | $$Ax^{2}$$ | $$Cy^{2}$$ |
| Eje de simetría | Vertical | Horizontal |
| Abertura | Hacia ariiba o abajo. | Hacia los lados. |
2. Cuando existe el término xy (B≠0) la curva cónica posee un eje de simetría oblicua.
3. Cuando los coeficientes D, E o F posee valores diferentes de cero, la parábola deja de estar centrada en el origen y su vértice se desplaza a otro punto del plano cartesiano.
4. Para distinguir si la ecuación general corresponde a una parábola, debe cumplirse la siguiente condición:
$$B^{2}=4AC$$
Ecuación de la tangente a la parábola
La ecuación de la tangente a una parábola permite obtener la recta que toca la curva cónica en un solo punto sin cortarla, es muy importante determinarla ya que sirve para analizar pendientes, identificar máximos o mínimos y resolver problemas de geometría y física relacionados con la parábola.
| Caso | Ecuación de la parábola | Ecuación de la tangente |
| Vértice en el origen, eje (y) (abre hacia arriba/abajo) | $$x^{2}=4py$$ | $$x\cdot x_1=2p(y + y_1)$$ |
| Vértice en el origen, (x) (abre a la derecha/izquierda) | $$y^{2}=4px$$ | $$y\cdot y_1=2p(x + x_1)$$ |
| Vértice en (h,k), eje paralelo a (y) (trasladada) | $$(x-h)^{2}=4p(y-k)$$ | $$(x-h)(x_1-h)=2p\big[(y-k)+(y_1-k)\big]$$ |
| Vértice en (h,k), eje paralelo a (x) (trasladada) | $$(y-k)^{2}=4p(x-h)$$ | $$(y-k)(y_1-k)=2p\big[(x-h)+(x_1-h)\big]$$ |
Ecuación de la tangente de pendiente m a la curva cónica
A continuación, te muestro la tabla donde se encuentran las ecuaciones de la tangente con pendiente m.
Donde m≠0
| Tipo | Tangente de pendiente m |
| Horizontal | $$y=mx+\left ( k-mh-\frac{p}{m} \right )$$ |
| Vertical | $$y=mx+(k-mh-pm^{2})$$ |
Transformación de la función cuadrática a su forma canónica con vértice (h,k) eje vertical
Cuando la función cuadrática se expresa de la siguiente forma:$$y=ax^{2}+bx+c$$
Su eje de simetría es paralelo al eje «y».
Para transformar la función cuadrática a su forma canónica con vértice (h,k) debes utilizar el método de completar cuadrados.
A continuación, su procedimiento:
$$y=ax^{2}+bx+c$$
1. Factorizar para que el primer término cuadrático sea uno.
$$y=a(x^{2}+\frac{b}{a}x)+c$$
2. Escoger el coeficiente del término lineal dividirlo entre dos y elevarlo al cuadrado.
$$\left ( \frac{\frac{b}{a}}{2} \right )^{2}=\frac{b^{2}}{4a^{2}}$$
3. El resultado anterior debe sumarse y restarse dentro de la expresión.
$$y=a\left ( x^{2}+\frac{b}{a}x+\frac{b^{2}}{4a^{2}}-\frac{b^{2}}{4a^{2}} \right )+c$$
4. Expresión obtenida.
$$y=a\left ( x^{2}+\frac{b}{a}x+\frac{b^{2}}{4a^{2}}\right )-\frac{\not ab^{2}}{4a^{\not 2}}+c$$
$$y=a\left ( x+\frac{b}{2a} \right )^{2}+\left ( c-\frac{b^{2}}{4a} \right )$$
5. Despejar para obtener la ecuación canónica
$$a\left ( x+\frac{b}{2a} \right )^{2}=y-\left ( c-\frac{b^{2}}{4a} \right )$$
$$a\left ( x+\frac{b}{2a} \right )^{2}=y-\left ( \frac{4ac-b^{2}}{4a} \right )$$
$$a\left ( x+\frac{b}{2a} \right )^{2}=y+\left ( \frac{b^{2}-4ac}{4a} \right )$$
$$\left ( x+\frac{b}{2a} \right )^{2}=\frac{1}{a}\left ( y+\frac{b^{2}-4ac}{4a} \right )$$
6. Comparar la ecuación canónica obtenida y la ecuación canónica de vértice (h,k).
Se comparan para poder obtener el parámetro y el vértice.
| Ecuación canónica obtenida | Ecuación canónica de vértice (h,k) |
| $$\left ( x+\frac{b}{2a} \right )^{2}=\frac{1}{a}\left ( y+\frac{b^{2}-4ac}{4a} \right )$$ | $$(x-h)^{2}=4p(y-k)$$ |
7. Coordenas del vértice y parámetro.
| Ecuación canónica obtenida | Ecuación canónica de vértice (h,k) |
| $$-h=\frac{b}{2a}\Rightarrow h=-\frac{b}{2a}$$ | $$4p=\frac{1}{4a}\Rightarrow p=\frac{1}{4a}$$ |
| $$-k=\frac{b-4ac}{4a}\Rightarrow k=\frac{4ac-b}{4a}$$ |
8. Vértice.
$$V\left (-\frac{b}{2a},\frac{4ac-b}{4a} \right )$$
9. Cóncavidad
| $$a> 0$$ | Cóncava hacia arriba y su vértice es un punto mínimo. |
| $$a< 0$$ | Cóncava hacia abajo y su vértice es un punto máximo. |
Resumen general
A continuación, te presento dos tablas con un resumen práctico que te será útil para que puedas comprender con facilidad los cálculos en los ejercicios explicados paso a paso.
Tabla resumen con vértice en (0,0)
| Eje de simetría horizontal | Eje de simetría vertical | |
| Ecuación general canónica | $$y^{2}=4px$$ | $$x^{2}=4py$$ |
| Foco | $$F(p,0)$$ | $$F(0,p)$$ |
| Directriz | $$x+p=0$$ | $$y+p=0$$ |
| Longitud del lado recto | $$Lr=|4\cdot p|$$ | $$Lr=|4\cdot p|$$ |
| Ecuación del eje de simetría | $$y=0$$ | $$x=0$$ |
Tabla resumen con vértice en (h,k)
| Eje de simetría horizontal | Eje de simetría vertical | |
| Ecuación general canónica | $$ (y-k)^{2} = 4p(x-h) $$< | $$ (x-h)^{2} = 4p(y-k) $$ |
| Foco | $$ F(h+p,k) $$ | $$ F(h,k+p) $$ |
| Directriz | $$ x = h – p $$ | $$ y = k – p $$ |
| Longitud del lado recto | $$ Lr = \lvert 4p \rvert $$ | $$ Lr = \lvert 4p \rvert $$ |
| Ecuación del eje de simetría | $$ y = k $$ | $$ x = h $$ |
Ejercicios explicados paso a paso
A continuación, 10 ejercicios explicados con un lenguaje sencillo y realizado paso a paso.
Ejercicio # 1
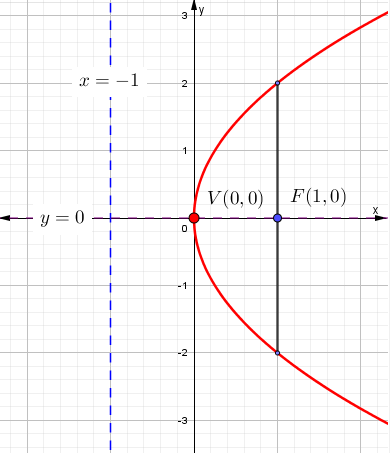
Encuentra los elementos y grafica cuya ecuación es:
$$y^{2}-4x=0$$
Solución
1. Transformar la ecuación a canónica.
$$y^{2}=4x$$
Es una curva cónica con eje de simetría en el eje «x»
2. Cálculo del parámetro (p).
Igualar la ecuación canónica y la canónica dada
| $$y^{2}=4px$$ | $$y^{2}=4x$$ |
$$4px=4x$$
Despejar
$$p=\frac{4x}{4x}$$
$$p=1$$
Como:
$$p>0$$
Es cóncava hacia la derecha o abre hacia la derecha.
3. Coordenadas del foco (F).
$$F(p,0)$$
Reemplazando el valor de p.
$$F(1,0)$$
4. Ecuación de la directriz.
$$x=-p$$
Reemplazar p
$$x=-1$$
5. Lado recto.
$$Lr=|4\cdot p|$$
Reemplazar el valor de p
$$Lr=|4\cdot 1|$$
$$Lr=4$$
6. Eje de simetría.
$$y=0$$
7. Gráfica
Ejercicio # 2
Encuentra los elementos y grafica cuya ecuación es: $$4x^{2}-8y=0$$
Solución
1. Transformar la ecuación a canónica.
Despejar ecuación dada lo cual resulta:
$$x^{2}=2y$$
Es una curva cónica con eje de simetría en el eje «y»
2. Cálculo del parámetro (p).
Igualar la ecuación canónica y la canónica dada
| $$x^{2}=4py$$ | $$x^{2}=2y$$ |
$$4py=2y$$
Despejar
$$p=\frac{2x}{4x}$$
$$p=\frac{1}{2}$$
Como:
$$p>0$$
Es cóncava hacia arriba o abre hacia arriba.
3. Coordenadas del foco (F).
$$F(0,p)$$
Reemplazando el valor de p.
$$F\left ( 0,\frac{1}{2} \right )$$
4. Ecuación de la directriz.
$$y=-p$$
Reemplazar p
$$x=-\frac{1}{2}$$
5. Lado recto.
$$Lr=|4p|$$
Reemplazar el valor de p
$$Lr=\left | 4\cdot \frac{1}{2}\right |$$
$$Lr=2$$
6. Eje de simetría.
$$x=0$$
7. Gráfica
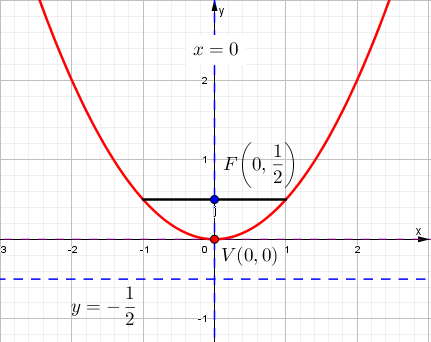
Ejercicio # 3
Graficar y determinar la ecuación de la parábola.
1. Vértice en el origen.
2. Foco (-5,0)
Solución:
1. Graficar el vértice, foco y trazado del eje de simetría
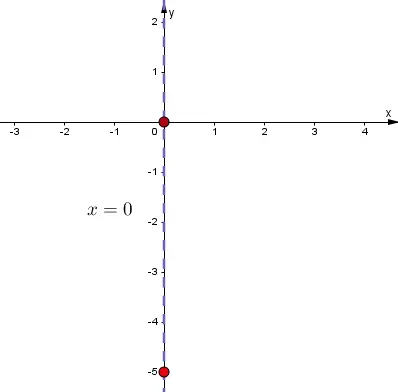
Nota:
- El eje de simetría coincide con el eje «y».
- Ecuación del eje de simetría:$$x=0$$
- Como el eje de simetría coincide con el eje «y» se utiliza la ecuación:$$x^{2}=4py$$
2. Definición de parámetro
$$p=-5$$
Por ser negativo (p<0) la parábola es cóncava hacia abajo.
3. Hallar la longitud del lado recto
$$Lr=|4\cdot p|$$
$$Lr=|4\cdot (-5)|$$
$$Lr=20$$
4. Ecuaciones
Parábola
$$x^{2}=4py$$
$$x^{2}=4\cdot (-5)y$$
$$x^{2}+20y=0$$
Canónica
$$x^{2}=-20y$$
Directriz
$$y=-p$$
$$y=-(-5)$$
$$y=5$$
5. Gráfica
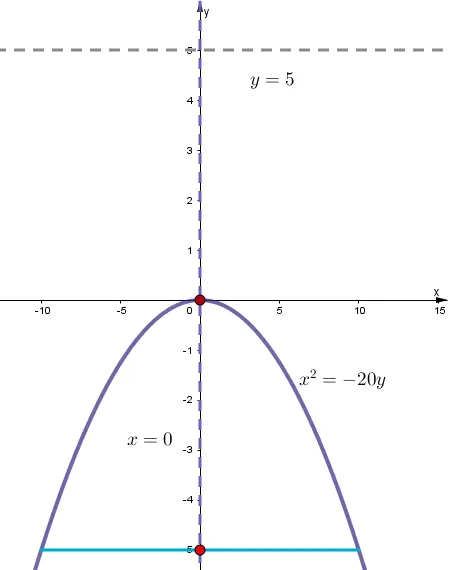
Ejercicio # 4
Graficar y determinar la ecuación de la parábola.
1. Vértice en el origen.
2. Directriz en la recta $$2y-5=0$$
Solución
1. Graficar el vértice, directriz y eje de simetría
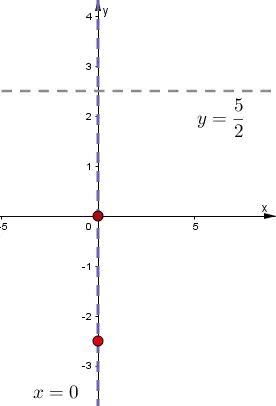 Nota:
Nota:
- El eje de simetría coincide con el eje «y».
- Ecuación del eje de simetría:$$x=0$$
- Para determinar ecuación se utiliza:$$x^{2}=4py$$
- Ecuación de la directriz:$$y=\frac{5}{2}$$
2. Definición del parámetro
$$p=-\frac{5}{2}$$
Es cóncava hacia abajo por$$p<0$$
3. Coordenadas del foco
$$F\left ( 0,-\frac{5}{2} \right )$$
4. Lado recto
$$Lr=\left | 4\cdot \left ( -\frac{5}{2} \right )\right |$$
$$Lr=10$$
5. Ecuación de la parábola y canónica
$$x^{2}=4py$$
Parábola
$$x^{2}=4\cdot \left ( -\frac{5}{2} \right )y$$
$$x^{2}+10y=0$$
Canónica
$$x^{2}=-10y$$
6. Gráfica
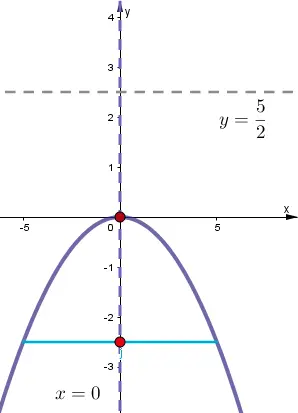
Ejercicio # 5
Graficar y determinar la ecuación de la parábola.
Directriz:$$3x+4=0$$
Solución
1. Cálculo del parámetro.
Como la ecuación de la directriz es:$$x+p=0$$
Se deduce que:
$$3x+4=0$$
$$3x=-4$$
$$x=-\frac{4}{3}$$
$$x+\frac{4}{3}=0$$
Por lo tanto el parámetro es:$$p=\frac{4}{3}$$
Cóncava hacia la derecha.
Con eje de simetría «x», entonces la forma de la ecuación es:$$y^{2}=4px$$
2. Cálculo de la ecuación.
$$y^{2}=4\cdot \frac{4}{3}x$$
$$y^{2}=\frac{16x}{3}$$
3. Foco.
$$F(p,0)$$
$$F\left ( \frac{4}{3},0 \right )$$
4. Lado recto.
$$Lr=\left | 4\cdot \left ( \frac{4}{3} \right )\right |$$
$$Lr=\frac{16}{3}$$
5. Gráfico
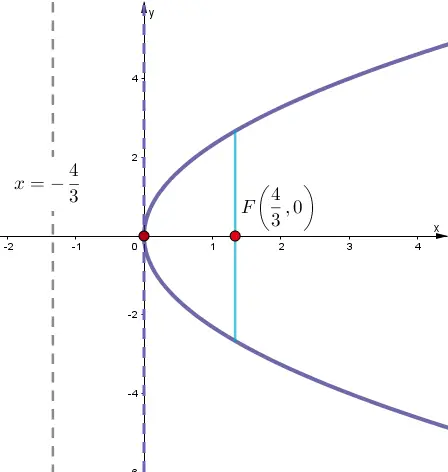
Ejercicio # 6
Dada la expresión:$$y^{2}=12x$$
Hallar: La ecuación de la tangente que pasa por el punto (3,-6)
Solución
- Según la ecuación dada el eje de simetría es horizontal.
- Antes de hallar la ecuación se comprueba que el punto está en la curva cónica.
1. Comprobación. Sustituir el punto en la ecuación dada
$$y^{2}=12x$$
$$(-6)^{2}=12\cdot 3$$
$$36=36$$
El punto se encuentra en la curva cónica.
2. Calculo del parámetro.
Se toma la ecuación dada y se iguala con la ecuación general canónica de una parábola.
$$y^{2}=12x$$
$$y^{2}=4px$$
$$12x=4px$$
$$p=3$$
3. Cáculo de la ecuación de la tangente:$$y\cdot y_1=2p(x + x_1)$$
Sustituir el punto (3,-6)
$$y\cdot (-6)=2\cdot 3(x + 3)$$
$$-6y=6(x + 3)$$
$$-6y=6x + 18$$
$$-6y-6x-18=0$$
Ejercicio # 7
Dada la expresión:$$x^{2}=8y$$
Hallar: La ecuación de la tangente de pendiente m=-2 y graficar.
Solución
- Según la ecuación dada el eje de simetría es vertical y con vértice en el origen.
1. Calculo del parámetro.
Se escoge la ecuación dada y se iguala con la ecuación general canónica de una parábola.
$$x^{2}=8y$$
$$y^{2}=4px$$
$$8y=4px$$
$$p=2$$
2. Calcular la ecuación tangente:$$y=mx+(k-mh-pm^{2})$$
Como el vértice está ubicado en el origen, la expresión se reduce a:$$y=mx+(-pm^{2})$$
Al sustituir los valores del parámetro y la pendiente dada, queda de esta forma:
$$y=-2x+(-2\cdot (-2)^{2})$$
$$y=-2x+(-8)$$
$$y=-2x-8$$
3. Gráfica
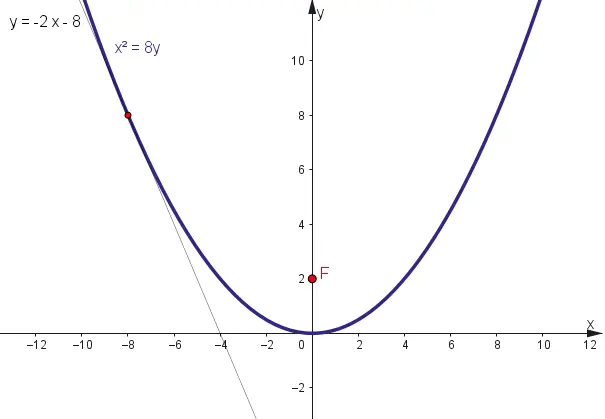
Ejercicio # 8
Dada la expresión:$$y^{2}+6x+6y=0$$
Hallar:
- Vértice.
- El eje.
- Foco.
- Lado recto.
- Ecuación de la directriz.
- Grafica.
Solución
La expresión dada es la ecuación general de la parábola de la forma:$$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$$
Donde:$$A=0;\; C\neq 0;\; D\neq 0$$
Haz clic aquí características resaltantes para que veas datos clave como eje de simetría, coeficientes, entre otros que te ayudará a comprender y ver la situación mucho más fácil.
Las características resaltantes recopiladas es la siguiente:
- Eje de simetría es horizontal es decir, paralelo al eje «x».
- Los coeficientes D y E distintos a ceros, demuestran que el vértice esta ubicado fuera del origen del plano cartesiano.
1. Transformar la ecuación dada a la forma canónica completando cuadrados.
$$y^{2}+6x+6y=0$$
$$y^{2}+6y=-6x$$
$$y^{2}+6y+9=-6x+9$$
$$y^{2}+6y+9=-6x+9$$
$$(y+3)^{2}=-6\left ( x-\frac{3}{2} \right )$$
2. Comparar con la general.
$$(y-k)^{2}=4p(x-h)$$
$$-k=3\Rightarrow k=-3$$
$$-h=-\frac{3}{2}\Rightarrow h=\frac{3}{2}$$
$$4p=-6\ \Rightarrow p=-\frac{3}{2}$$
$$k=-3;\;h=\frac{3}{2};\;p=-\frac{3}{2}$$
3. Elementos.
Vértice.$$V(h,k)=V\left ( \frac{3}{2},-3 \right )$$
Eje de simetría. Como pasa por el vértice:$$y=-3$$
Foco. El foco siempre se encuentra en el mismo eje que el vértice, para hallar sus coordenadas se suma la coordenada «x» del vertice y p.
$$F\left ( \frac{3}{2}-\frac{3}{2},-3 \right )$$
$$F(0,-3)$$
Lado recto.
$$Lr=\left | 4p\right |$$
$$Lr=\left | 4\cdot \left ( -\frac{3}{2} \right )\right |$$
$$Lr=6$$
Directriz. Como el eje de simetría es horizontal su ecuación a utilizar es: $$x+p=0$$
$$x=h-p$$
$$x=\frac{3}{2}–\frac{3}{2}$$
$$x=3$$
4. Gráfica.
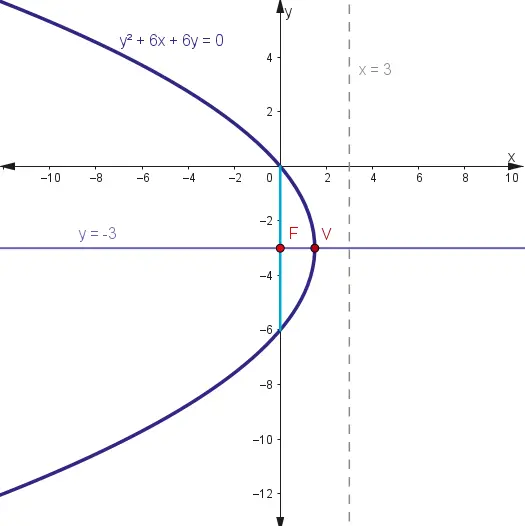
Ejercicio # 9
Dada la expresión:$$y=x^{2}+4x-6$$
Determinar:
- Vértice.
- Ecuación del eje de simetría.
- Foco.
- Lado recto.
- Directriz.
- Gráfico
Solución
La expresión dada es una función cuadrática de la forma:$$y=ax^{2}+bx+c$$
Donde:
$$a=1;\;b=4;\;c=-6$$
$$h=-\frac{b}{2a};\;k=\frac{4ac-b}{4a}$$
1. Cálculo del vértice.
$$V(h,k)$$
$$V\left ( -\frac{b}{2a},\frac{4ac-b^{2}}{4a} \right )$$
$$V\left ( -\frac{4}{2\cdot 1},\frac{4\cdot 1\cdot (-6)-(4)^{2}}{4\cdot 1} \right )$$
$$V\left ( -2,\frac{-40}{4} \right )$$
$$V\left ( -2,-10 \right )$$
2. Eje de simetría.
El eje es una recta paralela al eje «y» según la función dada.
$$x=-2$$
3. Cálculo del parámetro.
$$p=\frac{1}{4a}$$
$$p=\frac{1}{4\cdot 1}$$
$$p=\frac{1}{4}$$
4. Foco.
$$ F(h,\ k+p) $$
$$ F(-2,-10+p) $$
$$F\left ( -2, -10+\frac{1}{4} \right )$$
$$F\left ( -2,-\frac{39}{4} \right )$$
5. Lado recto.
$$ Lr = \lvert 4p \rvert $$
$$ Lr =\left | 4\cdot \frac{1}{4}\right |$$
$$Lr=1$$
6. Ecuación de la directriz.
$$ y = k – p $$
$$ y = -10 – \frac{1}{4} $$
$$y=-\frac{41}{4}$$
7. Gráfico.
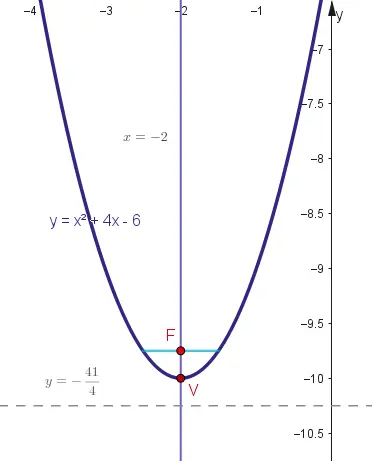
Ejercicio # 10
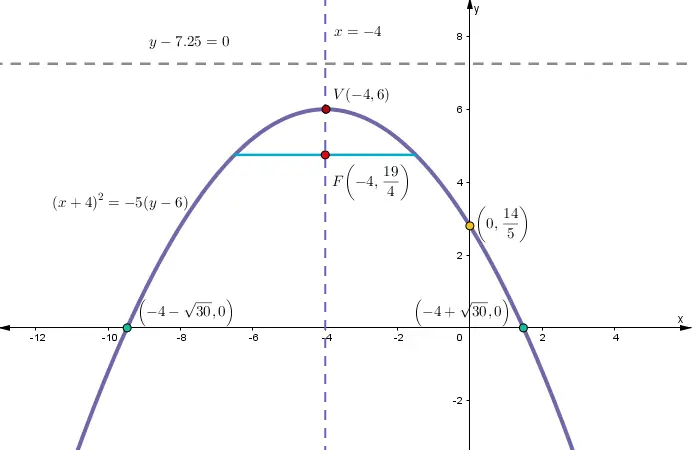
Dada la ecuación:$$(x + 4)^{2} = -5 (y – 6)$$
Determinar:
- Vértice.
- Ecuación del eje de simetría.
- Foco.
- Lado recto.
- Ecuación de la directriz.
- Interceptos eje «x» e «y».
- Gráfico.
Solución:
1. Comparar la ecuación dada con las de vértice (h,k).
Haz clic aquí para que veas la tabla resumen del vértice con (h, k) y seguir el proceso de forma más clara.
Al realizar la comparación se observa que su eje de simetría es paralelo al eje «y».
| Ecuación dada | Ecuación con vértice (h,k) |
| $$(x + 4)^{2} = -5 (y – 6)$$ | $$ (x-h)^{2} = 4p(y-k) $$ |
2. Coordenadas (h,k).
$$-h=4\Rightarrow h=-4$$
$$-k=-6\Rightarrow k=6$$
3. Vértice.
$$V(-4,6)$$
4. Ecuación del eje de simetría.
$$x=-4$$
5. Parámetro.
Gracias a la comparación se puede igualar y hallar el valor de p:$$4p=-5\Rightarrow p=-\frac{5}{4}$$
Como:$$p<0$$
Es cóncava hacia abajo.
6. Foco.
$$ F(h,k+p) $$
$$ F\left ( -4,6+\left ( -\frac{5}{4} \right ) \right ) $$
$$ F\left ( -4,\frac{19}{4} \right ) $$
7. Lado recto.
$$ Lr = \lvert 4p \rvert $$
$$Lr=\left | 4\cdot \left ( -\frac{5}{4} \right )\right |$$
$$Lr=5$$
8. Ecuación de la directriz.
$$ y = k – p $$
$$y=6-\left ( -\frac{5}{4} \right )$$
$$y=\frac{29}{4}$$
9. Cálculo de los interceptos
Dale clic aquí interceptos y allí verás su procedimiento.
Intercepto en «y»
$$(0 + 4)^{2} = -5 (y – 6)$$
$$16=-5y+30$$
$$y=\frac{14}{5}$$
Intercepto en «x»
$$(x + 4)^{2} = -5 (0 – 6)$$
$$(x + 4)^{2} = 30$$
$$x+4=\pm \sqrt{30}$$
$$\boxed{x=-4\pm \sqrt{30}}$$
$$x\approx 1,5$$
$$x\approx -9,5$$
9. Gráfico.
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
Modelación.
1. Determina la ecuación del lugar geométrico de todos los puntos del plano que equidistan del punto 𝑭(𝟎,𝟑) y de la recta 𝒚 + 𝟑 = 𝟎. Graficar.
2. Encuentra los elementos y grafica la parábola cuya ecuación es:$$y^{2}-8x=0$$
3. Hallar los elementos y construir la grafica cuya ecuación es:$$3x^{2}- 12y = 0$$
4. Hallar la ecuación de la parábola con vértice en el origen y directriz en la recta 𝒙 − 7 = 0. Graficar
5. Una parábola de vértice en el origen pasa por el punto (2,3) y su eje coincide con el eje «Y». Determine la ecuación y grafique.
6. Determinar los elementos de cada parábola y represéntalos gráficamente.
| $$\left ( y-\frac{7}{3}\right )^{2}=-3x$$ | $$\left ( x-4 \right )^{2}=9(y-3)$$ |
7. Determinar los elementos de cada parábola y grafícalas a partir de sus ecuaciones:
| $$\left ( x-h \right )^{2}=4p(y-k)$$ | $$\left ( y-k \right )^{2}=4p(x-h)$$ |
Razonamiento: Identifica los elementos correctos de la parábola
En cada caso, marca los elementos que NO correspondan a la parábola dada.
Caso 1
Ecuación:
(y - 2)² = 8(x + 1)Solución correcta
El único elemento incorrecto es el eje de simetría (debería ser y = 2).
Caso 2
Ecuación:
(x + 3)² = 12(y - 1)Solución correcta
El único elemento incorrecto es el eje de simetría (debería ser x = -3).
Caso 3
Ecuación:
(y + 1)² = -16(x - 2)Solución correcta
El único elemento incorrecto es el eje de simetría (debería ser y = -1).
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión

 1. Foco
1. Foco