¿Sabes cómo las funciones se aplica en la vida diaria? Un ejemplo sencillo lo vemos en una frutería:
¿Sabes cómo las funciones se aplica en la vida diaria? Un ejemplo sencillo lo vemos en una frutería:
Imagina que cada paquete de 4 manzanas se vende por un precio fijo. En este caso, el beneficio económico del negocio es una función de la cantidad de paquetes vendidos. Esto significa que la ganancia que se obtiene (y) depende directamente del número de paquetes que se vendan (x).
Función
| Es una relación que debe cumplir las siguientes condiciones: I- Todos los elementos del conjunto de partida deben poseer imágenes en el conjunto de llegada. II- Cada elemento del conjunto de partida sólo debe tener una imagen en el conjunto de llegada. |
Ejemplo.
Observa la figura y determina si las relaciones mostradas son funciones. justifica tu respuesta.
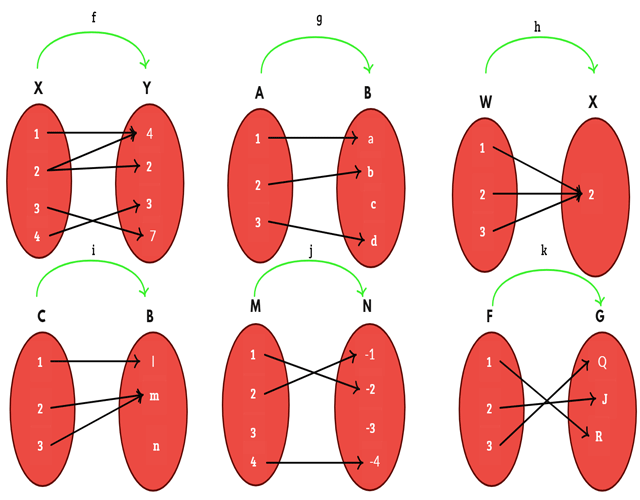
Respuesta:
a. En la relación f no es función porque el elemento 2 del conjunto de partida posee dos imágenes, 4 y 2, en el conjunto de llegada. Los pares ordenados formados son: f {(1,4),(2,4),(2,2),(3,7),(4,3)}
b. En la relación g a pesar que el elemento c del conjunto de llegada no esté relacionado si es función porque todos los elementos del conjunto de partida tienen una sola imagen. Los pares ordenados son: g {(1,a),(2,b),(3,d)}
c. En la relación h si es función porque todos los elementos del conjunto de partida tienen una sola imagen. Los pares ordenados son: h {(1,2),(2,2),(3,2)}
d. En la relación i es función porque todos los elementos del conjunto de partida tienen una sola imagen, a pesar que el elemento n del conjunto de llegada no esté relacionado. Los pares ordenados son: i {(1,l),(2,m),(3,m)}
e. En la relación j no es función porque el elemento 3 del conjunto de partida no está relacionado. Los pares ordenados son: j {(1,-2),(2,-1),(4,-4)}
f. En la relación k si es función porque todos los elementos del conjunto de partida tienen una sola imagen. Los pares ordenados son: j {(1,R),(2,J),(3,Q)}
Variable independiente y dependiente
En este caso, una variable es la cantidad o valor que puede cambiar. En el ejemplo de la frutería, tenemos dos variables en juego: la variable independiente y la variable dependiente.
La variable independiente (x) es la cantidad de paquetes de manzanas que los clientes compran, ya que su valor puede ser cualquier número. La variable dependiente (y) es el beneficio económico, porque su valor depende directamente de la cantidad de paquetes vendidos. Así, la ganancia es una función del número de paquetes que se venden.
Entonces:
x = variable independiente
f ( x ) = y = variable dependiente
Supongamos que en la frutería mencionada anteriormente colocan una promoción de la siguiente manera:
1 paquete de 4 manzanas por el precio de $5000
La expresión matemática:
f ( x ) = 5000x o y = 5000x
Donde:
“ x ” es el paquete de 4 manzanas, es decir, es la variable independiente.
“ y ” es el dinero por la venta que depende de las cantidades de paquetes de manzanas vendidas, entonces a esta letra se le llama variable dependiente.
“ f ( x ) ” esta expresión significa que la variable dependiente está en función a la variable independiente.
Para resumir todo:
La variable independiente la llamamos “variable” y
La variable dependiente “ función ”
Dominio y rango
El dominio de una función es el conjunto de todas las primeras componentes (x) de los pares ordenados, mientras que el rango es el conjunto de todas las segundas componentes (y).

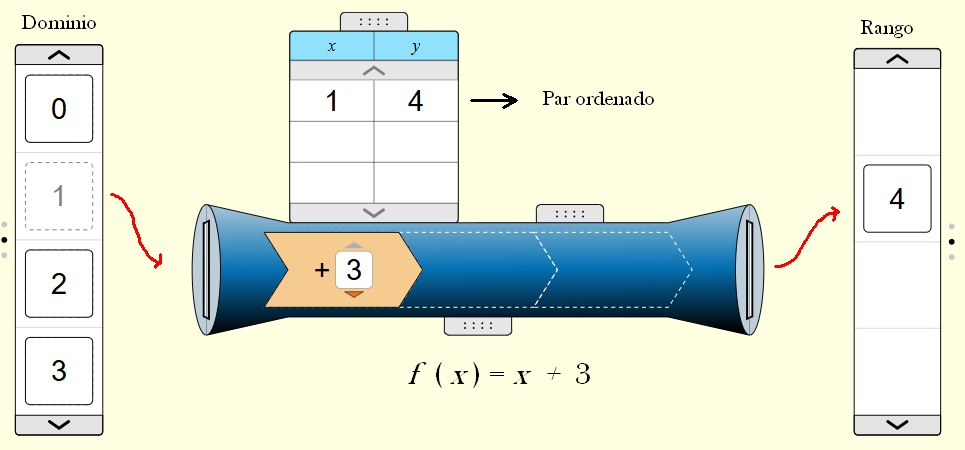
Observa la siguiente imagen. Allí se ilustra cómo la función, representada como un conducto, toma un valor del dominio (el conjunto de entrada) y lo transforma en un valor del rango (el conjunto de salida). El resultado de esta transformación es un par ordenado.
Función real de variable real
Es una relación matemática en la que tanto la variable independiente (x) como la variable dependiente (y) solo pueden tomar valores que pertenecen al conjunto de los números reales (R). En otras palabras, el dominio y el rango de la función son subconjuntos de los números reales.
Cuando se evalúa una función y el resultado no es un número real, entonces es indeterminada o indefinida en un punto específico. Esto ocurre en casos como la división por cero o la raíz cuadrada de un número negativo, que no tienen una solución dentro del conjunto de los números reales (R). Por ejemplo:$$f(x)=\sqrt{-3}$$
Laboratorio de las funciones
¡Llegó el momento de poner toda la teoría en práctica! Prepárate para experimentar con las funciones como si estuvieras en un laboratorio. A continuación, encontrarás una simulación interactiva de PhET, el Generador de Funciones, que te permitirá aprender jugando. Podrás manipular variables, observar cómo cambia la gráfica en tiempo real y entender la relación entre una fórmula y su representación visual. ¡Es la herramienta perfecta para dominar las funciones de una forma divertida y totalmente visual!
Restricciones del dominio
El dominio de una función se restringe cuando existen valores de la variable independiente (x) que, al ser evaluados, producen un resultado indeterminado o que no pertenece al conjunto de los números reales (R). En otras palabras, estos valores no son parte del dominio porque la función no está definida para ellos
Existen 3 tipos de restricciones en el dominio, ellos son:
I. Raíces de índices par
Para que la función$$f(x)=\sqrt{x+2}$$
Sea un número real, la expresión dentro de la raíz cuadrada no puede ser negativa.
Una raíz con índice par solo está definida para valores mayores o iguales a cero. Por lo tanto, para que el resultado no sea indeterminado, la cantidad subradical debe cumplir con la siguiente condición:
$$x+2\geq 0$$
$$x\geq -2$$
Dominio de la función$$D_{f}=[-2,\infty ]$$
II. Fracciones donde se anula el denominador
En la función$$f(x)=\frac{5}{x+1}$$
Existe una restricción en el denominador, ya que este debe ser diferente a cero. $$x+1\neq 0$$
$$x\neq -1$$
El dominio de la función es:
![]()
III. Fracciones donde se anula el denominador con raíces de índices par
Para estos de expresiones$$f(x)=\frac{\sqrt{x+1}}{x}$$
Debes considerar dos reglas tipos de restricciones:
- La raíz cuadrada con índice par.
- Fracciones que anulan el denominador.
Restricción del numerador:$$x+1\geq 0$$
$$x\geq -1$$
Restricción del denominador:$$x\neq 0$$
La solución es combinar las restricciones.
El dominio de la función es$$D_{f}=[-1,\infty )$$
Ejemplo.
Graficar las siguientes relaciones teniendo en cuenta el intervalo especificado para “x” y determinar el dominio, rango e indicar cuáles de ellas son funciones
a. F = {(x,y) / y = x2 ∧ 0 ≤ x < 3}
b. G = {(x,y) / y2 – x =2}
Solución
![]()
Tabla de valores
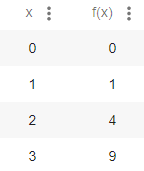
Para graficarla, primero traza cada par ordenado en el plano cartesiano y luego une los puntos para formar una curva suave. Para que la curva quede correctamente puedes utilizar la plantilla de Burmester.
Una vez que tengas la gráfica, aplica la prueba de la línea vertical para verificar si la expresión es una función. Si cualquier línea vertical que traces sobre la curva la toca en un solo punto, entonces la expresión dada es una función.
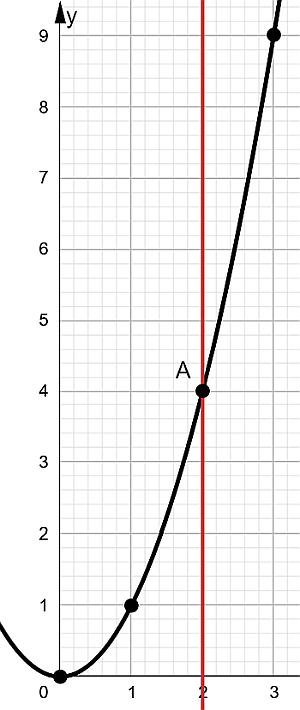
El dominio de la función es:$$D_{f} =[0,3)$$
Rango:$$R_{f} =[0,9)$$
Solución
![]()
$$y=\pm \sqrt{x+2}$$
Tabla de valores

Se grafica cada punto y luego se aplica la prueba de la línea vertical para saber si es función.
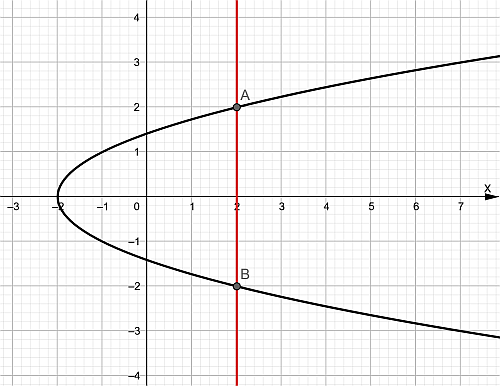
No es función porque la línea vertical toca dos puntos de la curva.
Dominio$$D_{f} =[-2,\infty )$$
Rango$$R_{f} =\mathbb{R}$$
Clasificación de las funciones
Las funciones se pueden clasificar según cómo se relacionan los elementos de su dominio con los de su rango. Esta clasificación permite conocer el comportamiento de una función y se clasifican en 3:
I. Inyectivas
Llamadas también uno a uno. Este tipo de función los elementos de partida deben ser distintos y también sus imágenes.
Ejemplo, observa el siguientes conjunto de pares ordenados: F{ ( 8 , 9 ) , ( 6 , 10 ) }.
Respuesta: Es una función inyectiva ya que los elementos del conjunto de partida comparten distintas imágenes.
Otro ejemplo de inyectiva es la expresada en la siguiente imagen
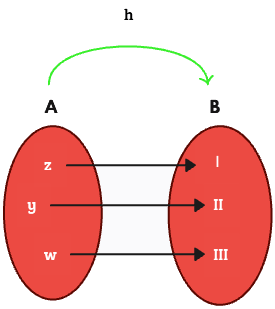
II. Sobreyectivas
Si el rango de la función es el mismo que el codominio es sobreyectiva.
Ejemplo:
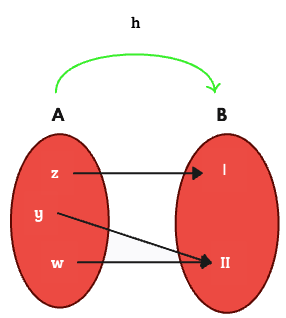
III. Biyectivas
Si es inyectiva y sobreyectiva a la vez.
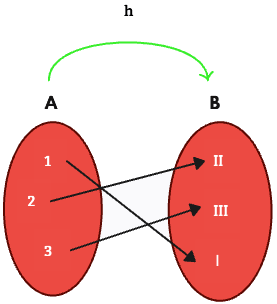
Ejemplo.
Indica el tipo de función, dominio y rango
f : [ 2 , ∞ ) → [ -1 , ∞ )
f ( x ) = x2 – 4x + 3
Solución:
$$f(x)=ax^{2}+bx+c$$
Donde:
a = 1 b = -4 c = 3
Cálculo del vértice
$$V(x,f(x))$$
$$V\left ( -\frac{b}{2a},f(x) \right )$$
$$x=-\frac{-4}{2\cdot 1}=2$$
$$f(2)=2^{2}-4\cdot 2+3=-1$$
$$f(2)=-1$$
$$V(2-1)$$
Cálculo de las intersecciones respecto al eje “x”$$y=0$$
$$f(x)=y$$
$$0=x^{2}-4x+3$$
Se factoriza y se iguala a cero los factores, finalmente se obtiene los valores de:
$$x_{1}=1$$
$$x_{2}=3$$
Gráfica
Se grafican los puntos y se aplica el criterio de la línea vertical y horizontal.
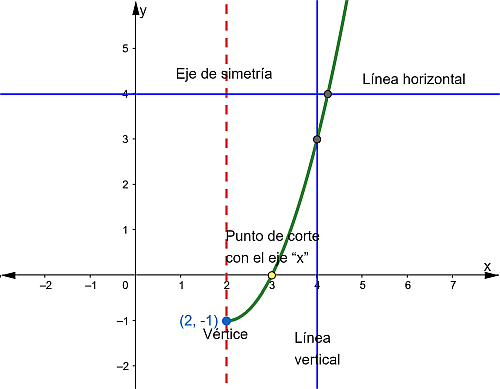
Cómo la línea vertical toca un punto de la curva, la expresión dada es función.
La línea horizontal toca un solo punto, entonces es inyectiva.
Dominio
$$D_{f}=[2,\infty )$$
Rango
$$R_{f}=[-1,\infty )$$
Codominio
$$C_{f}=R_{f}$$
Tipo de función
Biyectiva.
Características de las funciones
 Más allá de su clasificación, las funciones poseen características que dan a conocer su comportamiento y su forma gráfica.
Más allá de su clasificación, las funciones poseen características que dan a conocer su comportamiento y su forma gráfica.
Entre las más importantes se encuentran la simetría, su crecimiento y el decrecimiento, lo cual indica si sus valores aumentan o disminuyen a medida que se mueve de izquierda a derecha en el eje horizontal.
Simetría
La simetría es una de las características más interesantes de las funciones ya que revela si la curva posee una simetría axial (respecto a un eje) o central (respecto a un punto). Existe dos tipos de simetría y son llamadas:
I. Función par
Una función es par cuando la curva es simétrica respecto al eje y. Esta simetría es comprobable cuando se sustituye la variable x por -x en la función dada, generando la misma función original. Esto se expresa como:$$f(x)=f(-x)$$
Ejemplo. Determine si es par la siguiente función
$$f(x)=x^{2}+1$$
Solución:
Sustituir ( -x ) en la función:
f ( –x ) = ( -x )2 +1
f ( –x ) = x2 +1
Compara el resultado x2 +1 y la función dada. Ambas expresiones son iguales.$$x^{2}+1=x^{2}+1$$
Por lo tanto la función f ( x ) = x2 +1 es Par.
II. Función impar
Es una simetría central ya que es con respecto al origen del plano cartesiano. Analíticamente al sustituir “ -x ” la función debe dar negativa, satisfaciendo la relación:$$f(-x)=-f(x)$$
Ejemplo. Dada la función f ( x ) = x3, determine si es una función impar.
Solución:
Sustituir ( -x ) en la función, quedando:
f ( –x ) = ( -x )3
f ( –x ) = –x3
Es es una función Impar, ya que cumple la relación:$$f(-x)=-f(x)$$
Crecientes
Es creciente en un intervalo, si:
x1 < x2 por lo tanto f (x1) < f (x2)
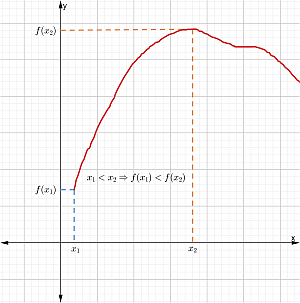
Entonces, si en un intervalo aumenta el dominio y el rango o disminuyen ambos, la función es creciente específicamente en ese intervalo.
Decrecientes
Una función es decreciente en un intervalo si, a medida que los valores de x aumentan, los valores de y (o f(x)) disminuyen.
x1 < x2 por lo tanto f (x1) > f (x2)
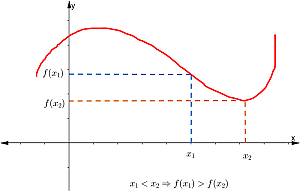
Funciones elementales
Las funciones elementales son las herramientas básicas de la matemática. A partir de ellas, se construyen funciones más complejas a través de operaciones como la suma, resta, multiplicación, división, potencias y raíces. Por esta razón, son esenciales para modelar una gran variedad de fenómenos en campos como la ciencia, la ingeniería y la economía. Ellas son:
- Funciones polinómicas
- Funciones racionales
- Funciones radicales
- Funciones trascendentes.
- Funciones especiales
Funciones racionales
Cuando se presenta de la siguiente manera f ( x ) = P ( x ) / Q ( x ) es una función racional, donde P ( x ) y Q ( x ) son polinomios.
Pasos para graficarla
- Factorizar si se puede.
- Determinar las raíces ( o cero) del numerador y del denominador los valores para lo cual la función no está definida.
- Hallar las asíntotas verticales, si existen.
- Hallar el intercepto con el eje “ y ”, es decir x = 0
- Determinar la asíntota horizontal, si existe.
- Crear la tabla de valores para obtener los puntos suficientes y así dibujar una buena curva.
Ejemplo.
Grafica y determina el dominio y rango de la función racional$$f(x)=\frac{x^{2}+x-2}{x^{2}+3x+2}$$
Solución
Factorización
$$f(x)=\frac{(x-1)\cdot (x+2)}{(x+1)\cdot (x+2)}$$
$$f(x)=\frac{x-1}{x+1}$$
La función posee un hueco (discontinuidad removible o evitable) en x = -2
El punto del hueco es P(-2,3)
Raíces (numerador y denominador)
x – 1 = 0 ⇒ x = 1
x + 1 = 0 ⇒ x = -1
Asíntotas verticales
x = -1
Intercepto con el eje “y”
x = 0
$$f(x)=y$$
$$y=\frac{0-1}{0+1}=-1$$
$$y=-1$$
Asíntota horizontal
Como el grado del polinomio del numerador y del denominador son iguales a 1, entonces la función f tiene una asíntota horizontal.
y = 1
Tabla de valores
Partiendo del dato de la asíntota vertical x = -1 se crea la tabla de valores

Gráfica
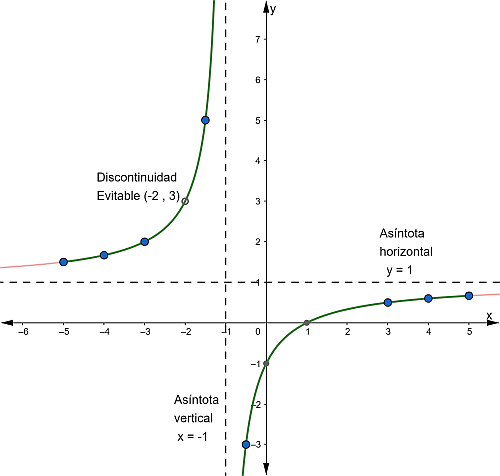
Dominio
Dom f = ℜ – { -2, -1 }
Rango
Rgo f = ℜ – { 1, 3 }
Funciones radicales
Son funciones que están expresadas por medio de una raíz. El dominio de este tipo de funciones depende directamente del índice de la raíz, lo que las clasifica en dos tipos principales:
Sí el índice es un número par, la función no está definida en los valores de x para los cuales el radicando es negativo. Para que la esté definida es necesario que la cantidad subradical sea mayor o igual a cero es decir aplicar una restricción del dominio.
Sí el índice es un número impar, el radicando puede ser cualquier número real (positivo, negativo o cero). La función está definida para todo el conjunto de los números reales. Sin embargo, se deben considerar las restricciones que existan dentro del radicando (por ejemplo, si este contiene un polinomio en el denominador).
Pasos para graficar una función radical
I. Se evalúa si posee índice par o impar.
Si la expresión viene dada en forma racional se determina en el numerador las raíces o los intercepto con el eje “ x ” y en el denominador los valores para los cuales la función no está definida.
Si es un radical con índice par y con una cantidad subradical en forma racional polinómica, se tiene que determinar el intervalo donde la función no está definida, para esto la expresión subradical debe ser mayor o igual que cero, luego el siguiente paso es resolver la inecuación racional.
II. Determina las asíntotas verticales, si existe.
III. Hallar el intercepto con el eje “ y ”.
IV. Determinar las asíntotas horizontales, si existe.
V. Crear la tabla de valores para obtener los puntos suficientes y así dibujar una buena curva.
Ejemplo 1.
Graficar y determinar dominio y rango de la función radical$$f(x)=\sqrt{\frac{2x+1}{3}}$$
Solución
Se aplica restricción para determinar el dominio.
$$\frac{2x+1}{3}\geq 0$$
$$2x+1\geq 0$$
$$2x\geq -1$$
$$x\geq -\frac{1}{2}$$
Dominio
Dom f = [ -1/2, ∞ )
Intercepto con el eje y
x = 0
$$y=\sqrt{\frac{2.0+1}{3}}$$
$$y=\sqrt{\frac{1}{3}}$$
$$y=\frac{1}{\sqrt{3}\cdot}\cdot \frac{\sqrt{3}}{\sqrt{3}}=$$
$$y=\frac{\sqrt{3}}{3}$$
Tabla de valores

Gráfica
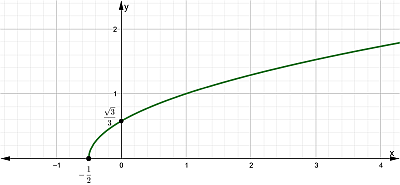
Rango
Rgo f = [ 0, ∞ )
Ejemplo 2.
Graficar y determinar el dominio y rango de la función radical$$f(x)=\frac{2}{\sqrt[4]{x+3}}$$
Es una función racional, con una raíz en el denominador de índice par.
Por estar en el denominador debe ser mayor que cero.
Y se evalúa los valores para los cuales la función no está definida
$$x+3> 0$$
$$x> -3$$
Es una función racional, pero el denominador es un radical por lo tanto no posee asíntotas verticales.
Intercepto con el eje y
x = 0
$$f(x)=y$$
$$y=\frac{2}{\sqrt[4]{0+3}}$$
$$y=\frac{2}{\sqrt[4]{3}}\cdot \frac{\sqrt[4]{3^{3}}}{\sqrt[4]{3^{3}}}$$
$$y=\frac{2\cdot \sqrt[4]{3^{3}}}{3}$$
$$y=\frac{2\cdot \sqrt[4]{27}}{3}$$
$$y\approx 1,52$$
Asíntota horizontal
Posee una asíntota horizontal ya que el grado del polinomio de la cantidad subradical es mayor que la del numerador.
Tabla de valores
| $$x$$ | $$f(x)$$ |
| $$-2$$ | $$2$$ |
| $$-1$$ | $$\sqrt[4]{8}$$ |
| $$0$$ | $$y=\frac{2\cdot \sqrt[4]{27}}{3}$$ |
| $$1$$ | $$\sqrt{2}$$ |
Gráfica
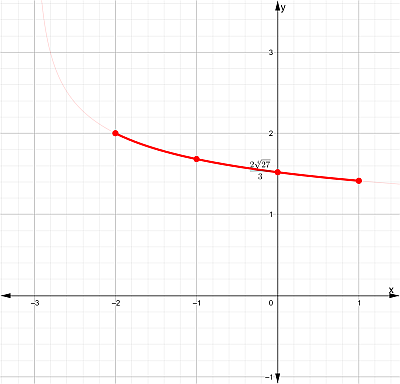
Dominio
Dom f = ( -3, ∞ )
Rango
Rgo f = ( 0, ∞ )
Ejemplo 3.
Graficar y determinar el dominio y rango de la función radical$$f(x)=\frac{\sqrt[3]{3x-1}}{x^{2}-1}$$
Solución
- Es una función racional, con una raíz en el numerador de índice impar.
- Se evalúa los valores para los cuales la función no está definida
$$x^{2}-1\neq 0$$
$$x^{2}\neq 1$$
$$x\neq \sqrt{1}$$
$$x\neq \pm 1$$
No esta definida para valores$$x\neq \pm 1$$
Intercepto con el eje “ x ” y = 0
$$f(x)=y=0$$
$$0=\frac{\sqrt[3]{3x-1}}{x^{2}-1}$$
$$0=\sqrt[3]{3x-1}$$
$$0=3x-1$$
$$x=\frac{1}{3}$$
Intercepto con el eje “ y ” x = 0
$$f(x)=y$$
$$y=\frac{\sqrt[3]{3\cdot 0-1}}{0^{2}-1}$$
$$y=1$$
Asíntotas verticales
$$x = 1$$
$$x = -1$$
Asíntota horizontal
Posee una asíntota horizontal en el eje “ x ” ya que el grado del polinomio de la cantidad subradical del numerador es menor que el grado del polinomio del denominador.$$y=0$$
Dominio
Dom f = ℜ – { – 1, 1 }
Rango
Rgo f = ℜ
Tabla de valores
| $$x$$ | $$f(x)$$ |
| $$-4$$ | $$\frac{\sqrt[3]{-13}}{15}$$ |
| $$-3$$ | $$\frac{\sqrt[3]{-10}}{8}$$ |
| $$-2$$ | $$\frac{\sqrt[3]{-7}}{3}$$ |
| $$-\frac{6}{5}$$ | $$\frac{25\sqrt[3]{-\frac{23}{5}}}{11}$$ |
| $$-\frac{4}{5}$$ | $$-\frac{25\sqrt[3]{-\frac{17}{5}}}{9}$$ |
| $$0$$ | $$1$$ |
| $$\frac{4}{5}$$ | $$-\frac{25\sqrt[3]{\frac{7}{5}}}{9}$$ |
| $$\frac{6}{5}$$ | $$\frac{25\sqrt[3]{\frac{13}{5}}}{11}$$ |
| $$2$$ | $$\frac{\sqrt[3]{5}}{3}$$ |
| $$3$$ | $$\frac{\sqrt[3]{8}}{3}$$ |
Gráfica
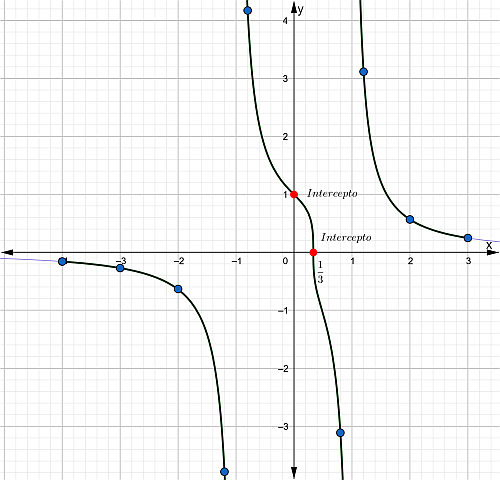
Ejemplo 4.
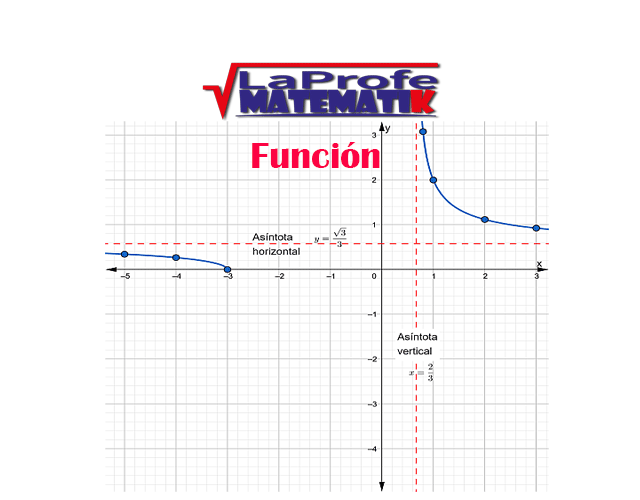
Grafique y determina el dominio y rango$$f(x)=\sqrt{\frac{x+3}{3x-2}}$$
Solución:
Se evalúa los valores para los cuales la función no está definida
$$\frac{x+3}{3x-2}\geq 0$$
$$3x-2\neq 0$$
Igualar el numerador y el denominador a cero para encontrar los puntos críticos que dividen la recta real en intervalos
$$x+3=0$$
$$x=-3$$
$$3x-2=0$$
$$x=\frac{2}{3}$$
Estudio del signo

Asíntota vertical
$$x=\frac{2}{3}$$
Asíntota horizontal
Posee asíntota horizontal (Cuando el grado del numerador = grado del denominador)
$$y=\frac{\sqrt{3}}{3}$$
Intercepto con el eje y
$$f(x)=y$$
$$y=\sqrt{\frac{0+3}{3\cdot 0-2}}$$
$$y=\infty $$
La curva no toca el eje y
Intercepto con el eje x
$$f(x)=y=0$$
$$0=\sqrt{\frac{x+3}{3x-2}}$$
$$x+3=0$$
$$x=-3$$
La curva toca el eje x por el punto (-3,0)
Dominio
$$D_{f}=( -\infty , -3]\cup ( 2/3 , \infty )$$
Rango
$$R_{f}=\left [ 0,\frac{\sqrt{3}}{3} \right )\cup \left ( \frac{\sqrt{3}}{3},\infty \right )$$
Tabla de valores
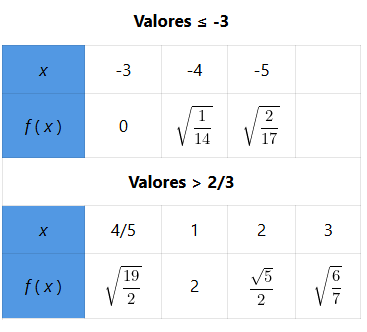
Gráfica
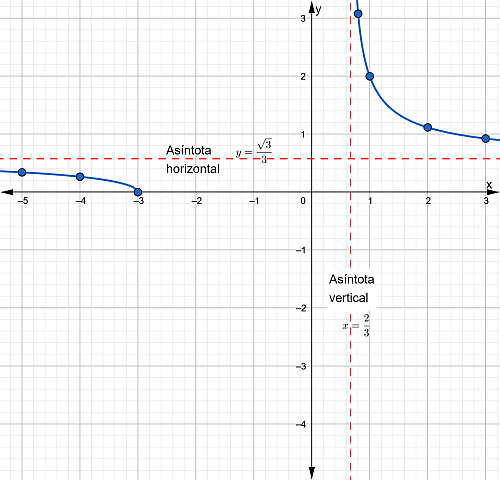
Operaciones con funciones
Las funciones pueden combinarse una con otras a través de las operaciones de la aritmética como la adición, sustracción, multiplicación y división y producir nuevas funciones.
Suma: ( f + g )( x ) = f ( x ) + g ( x )
Su dominio es:
Dom ( f + g ) = ( Dom f ∩ Dom g )
Resta: ( f – g )( x ) = f ( x ) – g ( x )
Su dominio es:
Dom ( f – g ) = ( Dom f ∩ Dom g )
Multiplicación: ( f . g )( x ) = f ( x ) . g ( x )
Su dominio es:
Dom ( f . g ) = ( Dom f ∩ Dom g )
División: ( f / g )( x ) = f ( x ) / g ( x )
Su dominio es:
Dom ( f / g ) = { x ∈ ( Dom f ∩ Dom g) / g ( x ) ≠ 0 }
Ejemplo.
Calcule la suma, diferencia, producto y el cociente de f y g y el dominio de cada función resultante.
![]()
![]()
![]()
![]()
![]()
Dominios resultante de cada operación:
Suma: Dom ( f + g ) = [ -3/2 , ∞ )
Resta: Dom ( f – g ) = [ -3/2 , ∞ )
Multiplicación: Dom ( f . g ) = [ -3/2 , ∞ )
División: Dom ( f / g ) = [ -3/2 , ∞ )
Actividades
Parte I
I. Determine si en cada planteamiento es una función. En caso de no serlo, proponer un ejemplo que muestre la situación.
a. El comportamiento de una bacteria está determinado por la expresión:
$$y=5e^{x}$$
b. Las muestras de sangre de un cultivo se describen por las parejas:
( 2 , 4), ( 4 , 8 ), ( 5 , 10), ( 6 , 12), ( 7 , 14 )
c. El valor de la producción cierta cantidad de cuadernos está dado por las parejas:
( 1 , 500 ), (2,600), ( 3 , 700 ), ( 4 , 800).
d. El movimiento de un cuerpo está dado por la expresión:
$$f=\frac{-47t^{2}}{2}$$
e. La cantidad de hombres que realizan un trabajo en cierto número de días es determinado por la expresión:
$$y=\frac{45}{x}$$
II. Construir una tabla de valores para cada función y su gráfica.
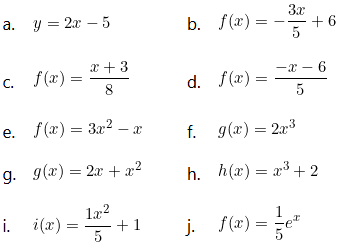
III. Diga cuáles de las siguientes curvas representan una función.
Gráfica # 1
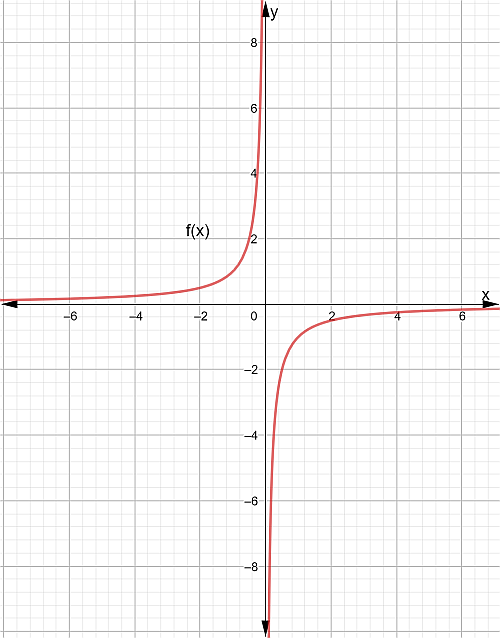
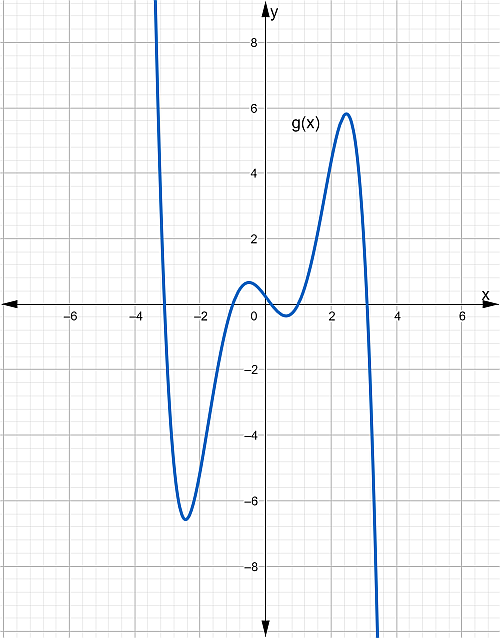
Gráfica # 2
IV. Calcula el valor de la función$$f(x)=\frac{3}{2}x^{2}-6$$
Para cada valor x dado
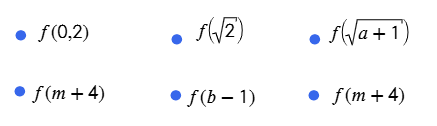
Parte II
I. Determine el dominio, rango, vértice, puntos de cortes, tabla de valores y gráfica de las siguientes funciones:
$$f(x)=6x^{2}-7x-3$$
$$f(x)=2x^{2}+3x-2$$
$$f(x)=x^{2}-9x+8$$
$$f(x)=-x^{2}-x+3$
II. Hallar el dominio, rango, interceptos, asíntotas, tabla de valores y gráfica de las siguiente funciones
$$f(x)=\frac{1}{x^{2}+1}$$
$$f(x)=\frac{x+4}{x+3}$$
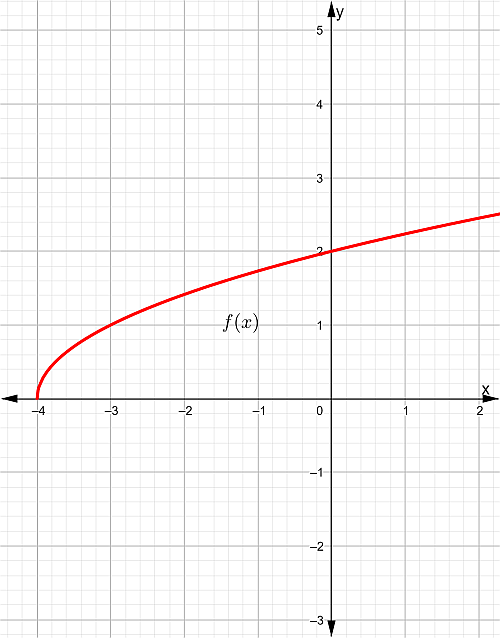
III. Hallar el dominio y el rango de las funciones cuyas gráficas se muestran a continuación. Determinar la ecuación que corresponda con cada gráfica.
Gráfica # 1
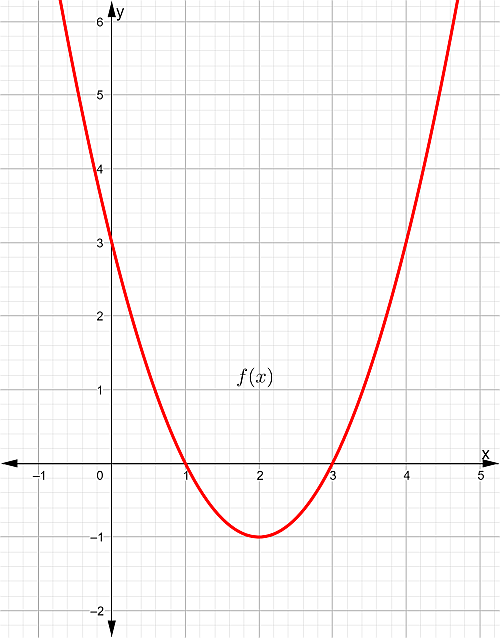
Gráfica # 2
Parte III
I. El valor de cada lápiz en un establecimiento es de $1500.
a. ¿La situación planteada describe una función?
b. Escribe la expresión algebraica que representa la función
c. Hallar el dominio y el rango de la función y explicar si los valores hallados tienen sentido.
II. El cargo básico del agua es de $60 y por cada m3 utilizados se cobran $2.
a. Escribe la expresión algebraica que describe el costo que se debe pagar en función a los m3 utilizados.
b. Hallar el dominio y el rango de la función
III. A continuación, se presentan diferentes formas de representación de funciones presentadas en tabla de valores, gráfica, pares ordenados. Determinar si es inyectiva, sobreyectiva o biyectiva
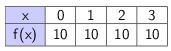
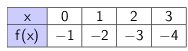
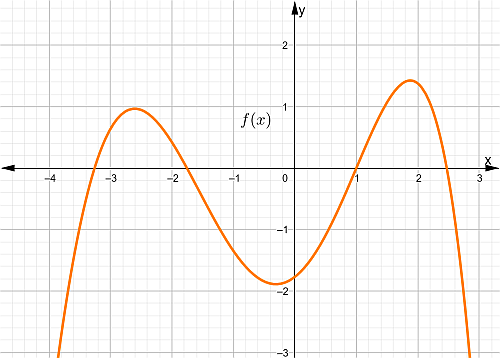
$$ \left{ (0,1),(2,3),(3,4),(4,5),(5,6)\right}$$
$$y=-x^{2}$$
Parte IV
I. Determinar cuáles de las siguientes funciones son inyectivas.
$$f(x)=3x-4$$
$$f(x)=x^{2}+2$$
$$f(x)=\frac{1}{x}$$
II. Problema.
Una fábrica de gaseosas define su producción a partir de la función f (x) = 5x, donde x representa los litros de gaseosas y f (x) es la cantidad de unidades por litro.
a. ¿La función de producción es biyectiva?
III. El costo que establece una fábrica de zapatos está determinado mediante la función:
$$f(x)=200x^{2}+150$$
donde x es la cantidad de zapatos fabricados y f (x) es el costo en pesos de la producción.
a. Determinar si f (x) es una función inyectiva.
b. Determinar si la función es biyectiva.
c. Graficar la función.
IV. Problema.
La distancia recorrida por una moto viene dada por la función f (t) = 10 + 3t2, donde t es el tiempo en segundos.
a. Determinar si la función es inyectiva
b. Determinar si es sobreyectiva
Parte V
I. Completa la siguiente tabla

II. Analiza y elabora la gráfica, especificando dominio, rango, puntos de cortes y asíntotas
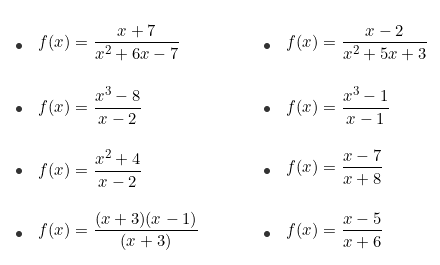
III. Analiza y elabora la gráfica, especificando dominio, rango, puntos de cortes
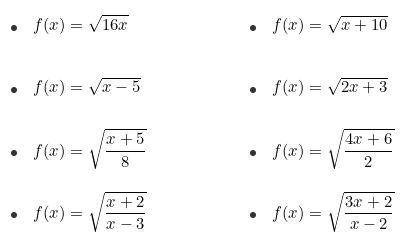
Parte VI
I. Para cada caso, determinar el dominio de todas las funciones
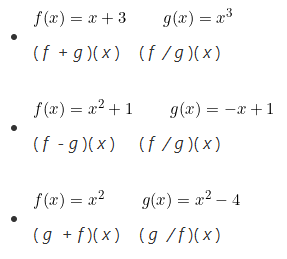
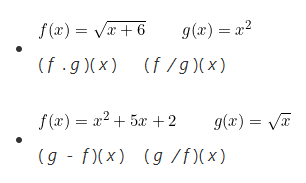
II. Dadas las funciones: f ( x ) = 4x + 3 ∧ g ( x ) = 4x2
Graficar:
- ( f + g )( x )
- ( f . g )( x )
- ( g / f )( x )
- ( g – f )( x )
- ( f – g )( x )
- ( f / g )( x )