¿Cómo resolver triángulos oblicuángulos? Aprende a usar la Ley del Seno y Coseno

4.4/5 - (5 votos)

¿Sabes qué son los triángulos oblicuángulos y cuáles son las leyes para solucionarlos? Esas leyes se llaman Ley del Seno y Ley del Coseno los dúos dinámicos diseñados para solucionar triángulos oblicuángulos.

Estas leyes son mucho más que fórmulas; son la base para calcular distancias en topografía, determinar la posición de un barco en el mar o diseñar estructuras arquitectónicas complejas. Dominar su aplicación te abre las puertas a campos fascinantes, dándote la capacidad de encontrar medidas y ángulos que no pueden ser calculados de forma directa.

Contenido del tema

¿Qué son los triángulos oblicuángulos?

Es una familia de triángulos compuesta únicamente por los obtusángulos y acutángulos. Esto quiere decir que los triángulos rectángulos no pertenecen a esta gran familia.

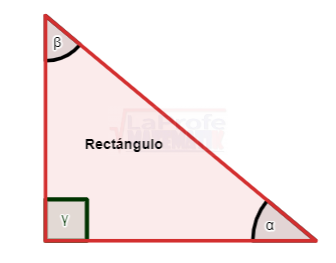Los triángulos rectángulos se solucionan aplicando tres métodos principales: el teorema de Pitágoras, razones trigonométricas y la propiedad de los ángulos complementarios ( α + β = 90° ).

Para solucionar los triángulos oblicuángulos debes determinar las medidas de sus tres lados y de sus tres ángulos internos. Para realizar esta gran hazaña debes adquirir unas herramientas súper poderosas llamadas: Ley del seno y Ley del coseno.

A continuación, te muestro a la honorable familia oblicuángulos:

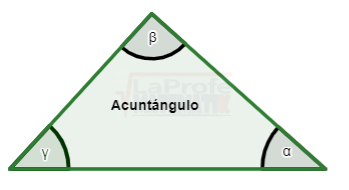
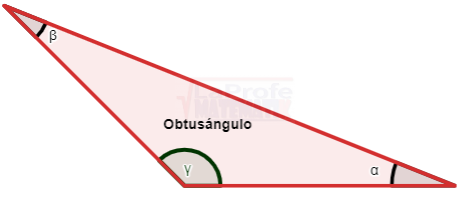
Casos para la resolución de triángulos oblicuángulos

Para la resolución de triángulos oblicuángulos se considera las medidas consecutivas y conocidas, por esta razón se hace posible identificar la resolución de estos tipos de triángulos en los siguientes cuatro casos:

1. Ángulo-Lado-Ángulo (A-L-A) o Lado-Ángulo-Ángulo (L-A-A)

Cuando un triángulo se conocen la medida de un lado y dos de sus ángulos, puede aparecer de la siguiente forma: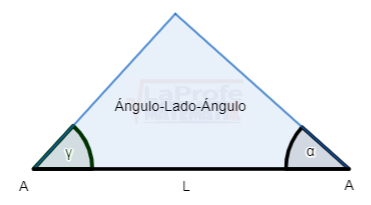

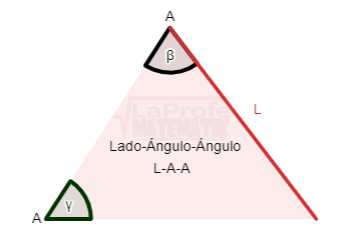
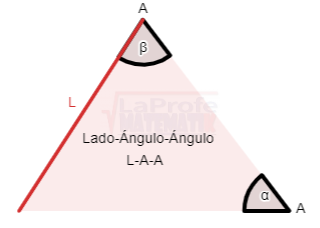
2. Lado-Lado-Ángulo (L-L-A)

Cuando un triángulo posee la medida de dos lados y un ángulo opuesto a algunos de ellos puede presentarse de la siguiente manera:

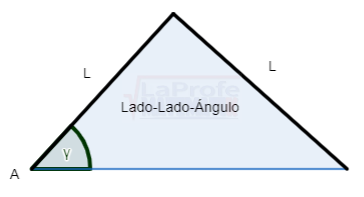
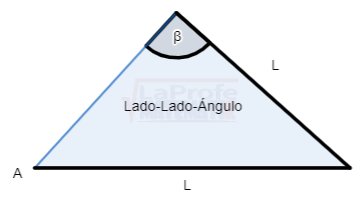
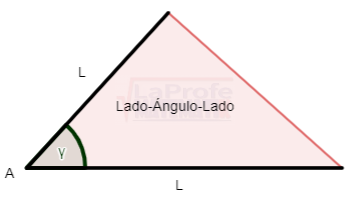
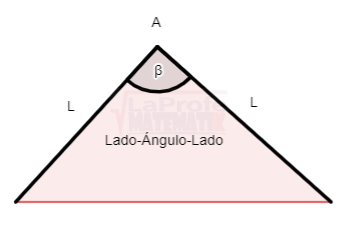
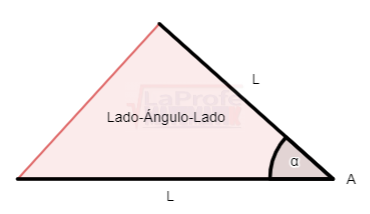
3. Lado-Ángulo-Lado (L-A-L)

Al conocer las dimensiones de dos lados y el ángulo comprendido entre ellos, los triángulos pueden presentarse de esta forma:

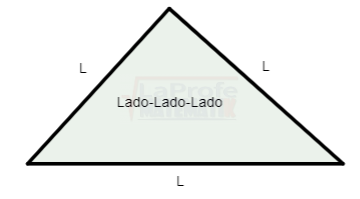
4. Lado-Lado-Lado (L-L-L)

Cuando se conocen las dimensiones de los tres lados del triángulo, solo aparece de esta manera:

Leyes para solucionar triángulos oblicuángulos

Para resolver los cuatro casos de triángulos oblicuángulos, es necesario aplicar dos leyes fundamentales: la Ley del Seno y la Ley del Coseno.

Ley del seno

La ley del seno permite determinar triángulos oblicuángulos, usando los casos # 1, y # 2. Es decir (A-L-A) (L-A-A) y (L-L-A)

La razón existente entre un lado del triángulo oblicuángulo y el seno de su ángulo opuesto a ese lado es proporcional a la misma razón con los otros lados y ángulos faltantes.

Ejemplo. Resuelva el siguiente triángulo acutángulo.

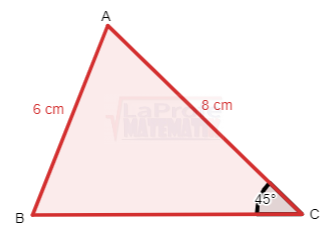
Solución:

Datos:

Tipo de caso: (L-L-A)

Ley del seno.

Lado a = ? → Ángulo opuesto α = ?

Lado b = 8cm. → Ángulo opuesto β = ?

Lado c = 6cm. → Ángulo opuesto δ = 45°

Procedimiento:

Determinar el valor del ángulo β.

Con los ángulos y , se determina el valor del ángulo α.

Se calcula el lado a

Problema.

Un estudiante diseñó un sistema biela-manivela para accionar un pistón. El largo de la manivela es de 2,2 in y 4,4 la longitud de la biela. Determine la distancia desde el centro (O) hasta el pistón (P). Ver la figura.

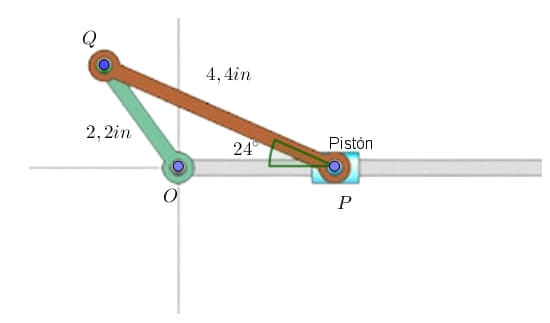
Solución:

Según la figura el triángulo formado es del tipo obtusángulo, los valores emitidos por el problema se ajusta a un tipo (L-A-L). Por lo tanto se aplica la ley del Seno.

$$\frac{a}{sen\alpha }=\frac{b}{sen\beta }=\frac{c}{sen\delta }$$

Datos:

$$a=2,2in$$

$$b=4,4in$$

$$\alpha = 24^{\circ }$$

I. Se determina el ángulo del centro (O) $\beta$

$$\frac{a}{sen\alpha }=\frac{b}{sen\beta }$$

$$sen\beta=\frac{b\cdot sen\alpha}{a}$$
$$sen\beta =\frac{4,4in\cdot sen24^{\circ }}{2,2in}$$
$$sen\approx 0,813$$

$$\beta =sen^{-1}\, 0,813\approx 54,39^{\circ }$$

Según la figura el ángulo opuesto del lado 4,4 in es del tipo obtuso, y el resultado obtenido es un ángulo agudo. Para este tipo de situaciones se determina su suplementario, quedando de la siguiente manera:

$$180^{\circ }=\beta+x\Rightarrow x=180^{\circ }-\beta$$

$$x=180^{\circ }-54,39^{\circ }=125,61^{\circ }$$

Por lo tanto el ángulo en el centro (O) es de $125,61^{\circ }$

II. Calculo de la distacia $\overline{OP}$

Aplicar la propiedad # 1 (suma de los ángulos internos) del triángulo para obtener el ángulo $\delta$

$$180^{\circ }=\alpha +\beta +\delta \Rightarrow$$
$$ \delta=180^{\circ }-\alpha -\beta$$

$$ \delta=180^{\circ }-24^{\circ } -125,61^{\circ }$$
$$\boxed{\delta= 30,39^{\circ }}$$

$$\frac{c}{sen\delta }=\frac{a}{sen\alpha }\Rightarrow $$
$$c=\frac{a\cdot sen\delta }{sen\alpha }$$
$$=\frac{2,2in\cdot sen30,39^{\circ }}{sen24^{\circ }}$$
$$\boxed{c\approx 2,7in}$$

La distancia del centro (O) hasta el pistón (P) es de 2,7 in.

Ley del coseno

La ley del coseno permite determinar triángulos oblicuángulos, usando únicamente los casos # 3 y # 4. Es decir (L-A-L) y (L-L-L).

El cuadrado de la longitud de uno de sus lados es igual a la suma de los cuadrados de sus longitudes de los otros dos lados menos el doble producto de esas longitudes por el coseno del ángulo comprendido entre ellos.$$a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot cos\alpha $$

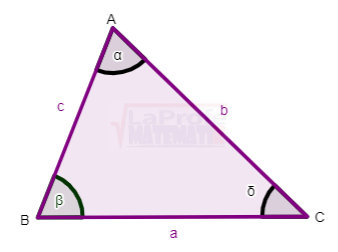
Fórmulas

A continuación, las fórmulas para determinar los lados y ángulos:

Lados

$$a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot cos\alpha $$

$$b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot cos\beta $$

$$c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot cos\delta $$

Ángulos

$$\alpha = cos^{-1}\cdot \left ( \frac{b^2 + c^2 – a^2}{2bc} \right )$$

$$\beta = cos^{-1}\cdot \left ( \frac{a^2 + c^2 – b^2}{2ac} \right )$$

$$\delta = cos^{-1}\cdot \left ( \frac{a^2 + b^2 – c^2}{2ab} \right )$$

Ejemplo. Resuelva el siguiente triángulo.

Solución

Datos

Obtusángulo.

Caso: (L-A-L).

Ley del coseno.

Lado a = 5cm → Ángulo opuesto α = ?

Lado b = ? → Ángulo opuesto β = 120°

Lado c = 10cm. → Ángulo opuesto δ = ?

Procedimiento:

Determinar el valor del lado b

Sustituir todos los valores de los lados en la fórmula y luego se determina el ángulo α.

Determinar el ángulo δ

Actividades

Solucione los siguientes triángulos y ¿Qué ley debes aplicar?

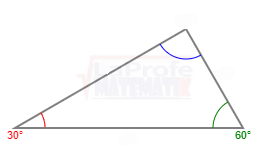
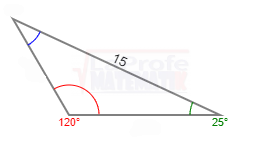
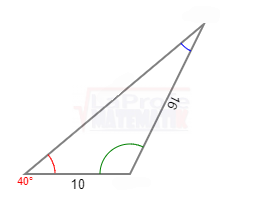
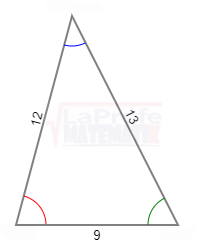
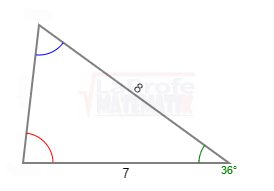
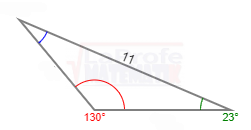
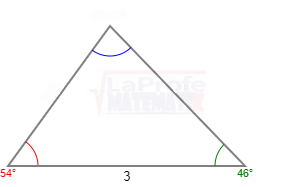
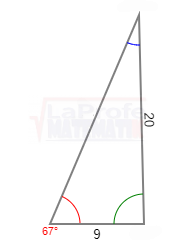
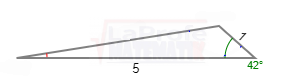
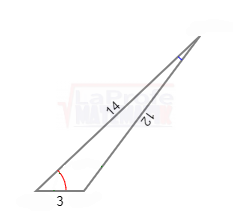
Un avión partió de la ciudad «X» con destino a la ciudad «Z», que se encuentra a una distancia de 150 millas, y luego se dirige hacia la ciudad «Y», que está a 100 millas de distancia. Consulte la imagen adjunta.