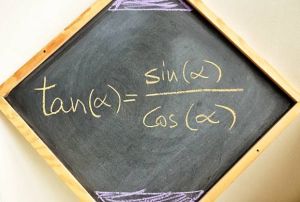
¿Alguna vez te has preguntado cómo las razones trigonométricas se usan para calcular la altura de un edificio o la distancia a un objeto sin tener que medirlos directamente? La solución a este tipo de desafíos se encuentra en la trigonometría. El origen y el valor de estas razones se comprenden mejor al visualizar la circunferencia trigonométrica.
En este post no solo aprenderás a aplicar las razones trigonométricas de manera sencilla, sino que también te mostraremos los diferentes casos para resolver triángulos rectángulos con ejemplos prácticos.
Identificación de los catetos
Los ángulos en posición normal son aquellos que son utilizados en las razones trigonométricas.
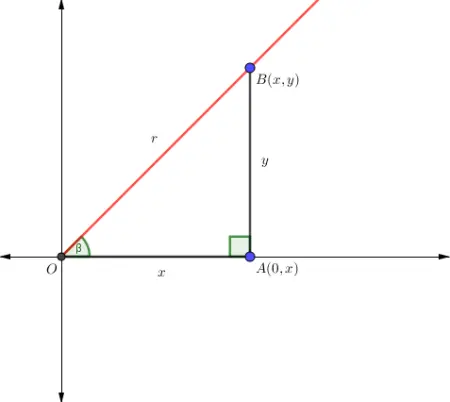
1. Se tiene un ángulo β en posición normal, el punto de coordenada B(x,y) ubicado en el lado final del ángulo (I Cuadrante), el punto de coordenada A(0,x) ubicado en el lado inicial del ángulo, entonces el segmento 
es perpendicular al eje “x”, obteniéndose un triángulo 
rectángulo.
2. El segmento 
es la hipotenusa = r , el segmento 
es el cateto adyacente al ángulo β y el segmento 
es el cateto opuesto al ángulo β, la medida del cateto adyacente = x y la medida del cateto opuesto = y .
3. Para darle el nombre a los catetos se debe tomar en cuenta su posición con respecto al ángulo β, el cateto adyacente es el lado del triángulo que está mas cerca al ángulo β y el cateto opuesto es el lado del triángulo que está al frente del ángulo β.
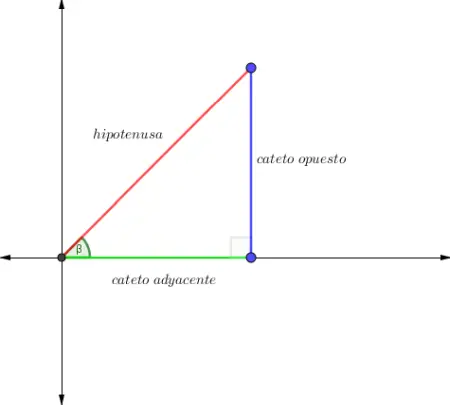
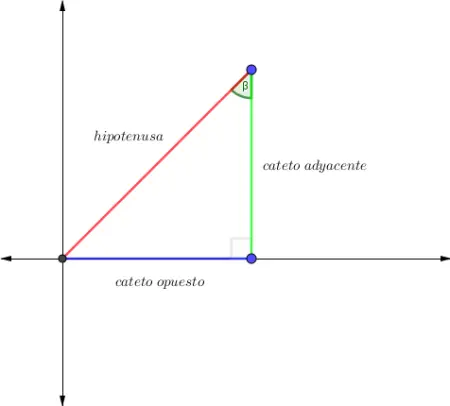
Mira las imágenes de abajo el ángulo β se posiciona en dos vértices del triángulo por lo tanto los catetos opuesto y adyacente cambian de posición.
 |  |
Razones trigonométricas en el triángulo rectángulo
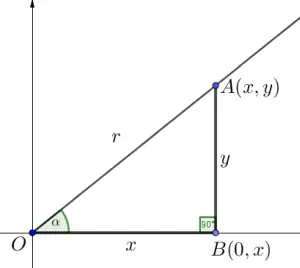
En el triángulo rectángulo se definen las 3 razones trigonométricas y sus recíprocas, tenga en cuenta que:
| Cateto opuesto = y |
| Cateto adyacente = x |
| Hipotenusa = r |
Las 3 razones trigonométricas y sus recíprocas (inversas) son las siguientes:
- Seno (sen) → Cosecante (csc)
- Coseno (cos) → Secante (sec)
- Tangente (tan) → Cotangente (cot)
¿Qué es el seno?
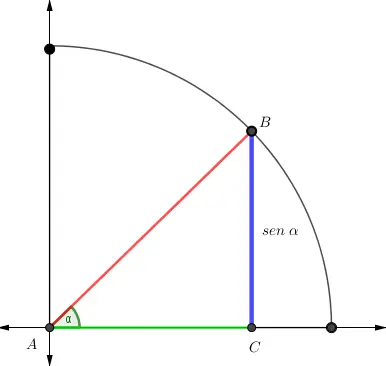
El seno del ángulo α es la razón entre la altura (cateto opuesto) y la hipotenusa del triángulo rectángulo. Es decir, el seno mide qué tan alta es la figura en comparación con la longitud de la hipotenusa.
$$sen\alpha =\frac{cateto\; opuesto}{hipotenusa}=\frac{y}{r}$$
Representación geométrica del seno
Su representación geométrica es la siguiente:
¿Qué es el coseno?
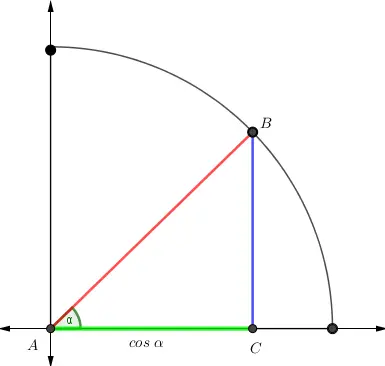
El coseno del ángulo α es la razón entre la base (cateto adyacente) y la hipotenusa. Es decir, el coseno mide qué tan largo es la base en comparación con la longitud de la hipotenusa.
$$cos\alpha =\frac{cateto\; adyacente}{hipotenusa}=\frac{x}{r}$$
Representación geométrica del coseno
Geométricamente, el coseno indica qué parte de la hipotenusa corresponde a la base del triángulo rectángulo.
¿Qué es la tangente?
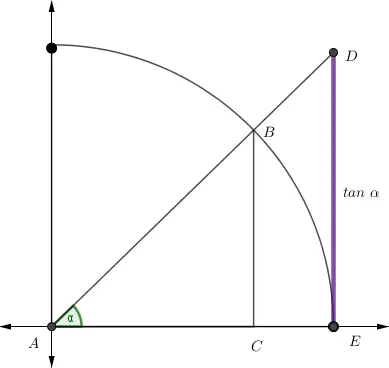
La tangente del ángulo α es la razón entre el cateto opuesto y el cateto adyacente, es decir, compara la altura con la base del triángulo rectángulo.
$$tan\alpha =\frac{cateto\; opuesto}{cateto \; adyacente}=\frac{y}{x}$$
Esta razón permite determinar qué tan inclinada está la recta que forma el ángulo α con la horizontal. En el triángulo, dicha recta corresponde a la hipotenusa ( r ); al prolongarla, su inclinación se interpreta como la pendiente de la recta. Por ello, la tangente indica cuánto se eleva verticalmente una recta por cada unidad que avanza horizontalmente: cuanto mayor es la tangente, más empinada es la recta.
Representación geométrica de la tangente
Al prolongar la hipotenusa, su inclinación puede interpretarse como la pendiente de la recta; por ello, la tangente indica cuánto se eleva verticalmente la recta por cada unidad que avanza horizontalmente.
Tangente = pendiente = cuánto sube por cada unidad que avanza.
¿Qué es la cosecante?
La cosecante del ángulo α es la razón entre la hipotenusa y el cateto opuesto.
$$csc\alpha =\frac{hipotenusa}{cateto \; opuesto}=\frac{r}{y}$$
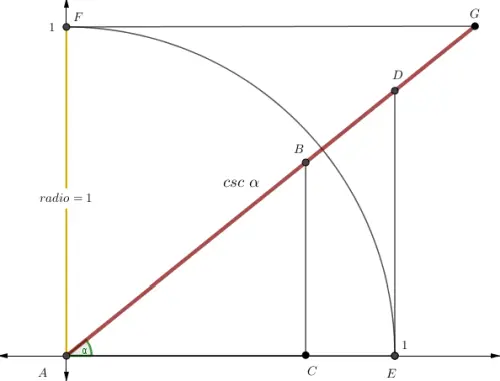
Geométricamente, la cosecante indica cuánto debe estirarse la hipotenusa ( r ) que forma el ángulo α para alcanzar una altura de una unidad, por lo que se interpreta como la inversa del seno.
$$csc\: \alpha =\frac{1}{sen\: \alpha }$$
Representación geométrica de la cosecante
Mientras el seno muestra la altura que se alcanza con una hipotenusa de longitud 1, la cosecante indica qué longitud debe tener la hipotenusa para alcanzar una altura de 1.
¿Qué es la secante?
La secante de un ángulo es la razón entre la hipotenusa y el cateto adyacente.
$$sec\alpha =\frac{hipotenusa}{cateto \; adyacente}=\frac{r}{x}$$
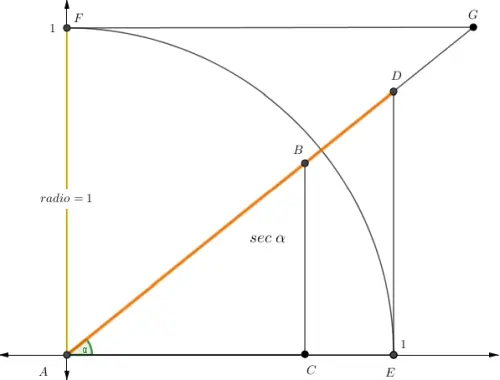
En términos geométricos, la secante indica cuánto debe alargarse la hipotenusa que forma el ángulo α para alcanzar una base de una unidad, por lo que se interpreta como el inverso del coseno.
$$sec\: \alpha =\frac{1}{cos\: \alpha }$$
Representación geométrica de la secante
Mientras el coseno muestra un cateto adyacente que se obtiene con una hipotenusa de longitud 1, la secante indica qué longitud debe tener la hipotenusa para obtener un cateto adyacente de 1.
¿Qué es la cotangente?
La cotangente de un ángulo es la razón entre el cateto adyacente y el cateto opuesto, es decir, compara la base con la altura del triángulo rectángulo.
$$cot\alpha =\frac{cateto\;adyacente}{cateto \; opuesto}=\frac{x}{y}$$
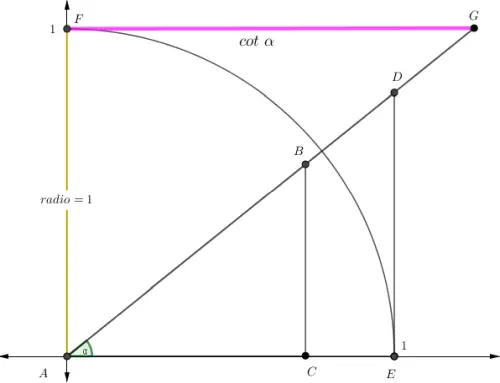
Esta razón indica cuánto se avanza horizontalmente por cada unidad que se eleva verticalmente. Por ello, la cotangente describe la inclinación horizontal de la recta que forma el ángulo α con la horizontal, y puede interpretarse como la inversa de la pendiente o simplemente la inversa de la tangente.
$$tan\: \alpha =\frac{1}{cot\: \alpha }$$
Representación geométrica de la cotangente
Mientras la tangente muestra cuánto se sube por cada unidad que se avanza, la cotangente indica cuánto se avanza para subir una unidad.
Ejemplos resueltos
Determinar los valores de las razones trigonométricas sen α, cos α y tan α en el triángulo
Solución:
Datos:
Se aplica Pitágoras para determinar el valor de la hipotenusa 
Se calcula las 3 razones trigonométricas del ángulo α
$$sen\alpha =\frac{y}{r}=\frac{3}{5}$$
$$cos\alpha =\frac{x}{r}=\frac{4}{5}$$
$$tan\alpha =\frac{y}{x}=\frac{3}{4}$$
Razones trigonométricas para ángulos complementarios
Los ángulos α y β son complementarios, ya que 
. Esto quiere decir que α es el complemento de β y β es el complemento de α.
En el triángulo BAC, los ángulos α y β son complementarios y se cumple que:
sen α = cos β tan α = cot β sec α = csc β
sen β = cos α tan β = cot α sec β = csc α
Las relaciones entre este tipo de razones trigonométricas se conocen como cofuncionalidad.
¿Qué son las cofunciones?
El prefijo “co” significa “complemento”, entonces:
Coseno = seno del ángulo complementario.
Cotangente = tangente del ángulo complementario.
Cosecante = secante del ángulo complementario.
Dos funciones trigonométricas son cofunciones cuando una se obtiene evaluando la otra en el ángulo complementario. Dicho de otra manera: Es la relación que existe entre dos funciones trigonométricas cuando el valor de una función evaluada en un ángulo es igual al valor de su cofunción evaluada en el ángulo complementario. |
Como la relación de ángulos complementarios es: α + β = 90° el valor de β y α queda de la siguiente forma:
$$\beta =90^{\circ }-\alpha $$
$$\alpha =90^{\circ }-\beta $$
Razón trigonométrica α (Rtα) = Razón trigonométrica opuesta β (Rtoβ).
sen α = cos β
$$sen\, \alpha =cos\left ( 90^{\circ } – \alpha \right )$$
Rt ( β ) = Rto ( α ) , con β = 90° – α
$$sen(90^{\circ }-\alpha )=cos\alpha $$
$$tan(90^{\circ }-\alpha )=cot\alpha $$
$$sec(90^{\circ }-\alpha )=csc\alpha $$
Debes tener en cuenta, para los ejercicios que verás más adelante, la siguiente forma de escritura:
cateto opuesto = co
cateto adyacente = ca
hipotenusa = h
El cateto adyacente del ángulo α es el cateto opuesto del ángulo β y el cateto opuesto del ángulo α es el cateto adyacente del ángulo β.
Esto quiere decir que el valor de una razón trigonométrica de un ángulo en un triángulo rectángulo es lo mismo que la razón trigonométrica opuesta del ángulo complementario.
Ejercicios prácticos
Primero. Mira las siguientes relaciones.
Segundo. Dados dos ángulos complementarios, hallar las razones trigonométricas cuyo valores sean los mismos.
- El ángulo de α = 60° y el ángulo de β = 30° son complementarios, el valor de$$sen30^{\circ }=cos60^{\circ }=\frac{1}{2}$$
- También los ángulos de β = 45° y α = 45° son complementarios, esto quiere decir que$$tan45^{\circ }=ctg45^{\circ }=1$$
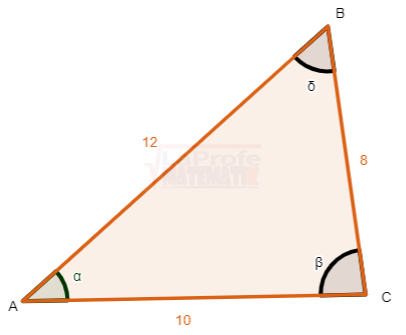
Tercero: Determina, las razones trigonométricas del seno α, coseno δ del siguiente triángulo rectángulo.
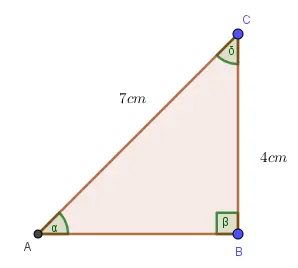
Como los ángulos δ y α son complementarios, el sen α = cos δ . Se tiene lo siguiente:
Sumando ambos ángulos para comprobar:
Se puede observar claramente que la sumatoria de los ángulos α y ð son complementarios.
Laboratorio de las razones trigonométricas
¡Ha llegado el momento de la verdad! Prepárate para poner a prueba todo lo que has aprendido. A continuación, encontrarás un simulador de razones trigonométricas, una herramienta fantástica para que aprendas jugando y fortalezcas tus conocimientos de una forma interactiva y divertida. ¡Es la oportunidad perfecta para llevar tus habilidades al siguiente nivel!
Casos para resolver triángulos rectángulos
Resolver un triángulo significa buscar todas sus dimensiones, es decir conocer las medidas de los tres lados y los tres ángulos.
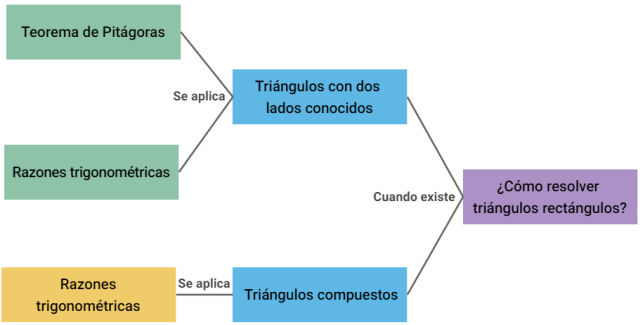
Triángulos con dos lados conocidos
Existen dos formas para resolver este tipo de casos: aplicando el teorema de Pitágoras o las razones trigonométricas.
Teorema de Pitágoras
Para determinar el lado faltante debes aplicar el teorema de Pitágoras.
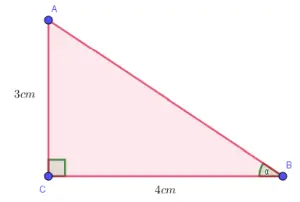
Ejemplo. Resolver el triángulo ABC cuyos valores de los catetos se muestran en la imagen.
Solución:
Observa que en el triángulo se desconoce el valor de la hipotenusa y de los ángulos α y β
Se aplica el teorema de Pitágoras para determinar la hipotenusa
Se aplica las razones trigonométricas para hallar los ángulos α y β.
Como α y β son complementarios se aplica:
Ejemplo: Resolver el triángulo usando solo las razones trigonométricas
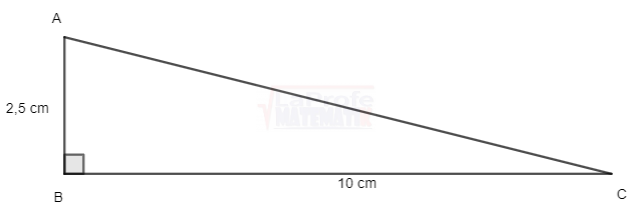Observa que en el triángulo se desconoce los valores de la hipotenusa y los ángulos del vértice A y C
Se posee dos catetos del triángulo, entonces la razón trigonométrica que se va aplicar es la tangente, haciendo uso del ángulo 
Se aplica la inversa para obtener el valor del ángulo:
Como la sumatoria de los ángulos 
, por ser complementarios
Se calcula la hipotenusa aplicando la razón trigonométrica del del seno
Ejemplo. Resolver el triángulo compuesto usando solo las razones trigonométricas.
Los triángulos compuestos son triángulos rectángulos compuestos por dos o más triángulos.
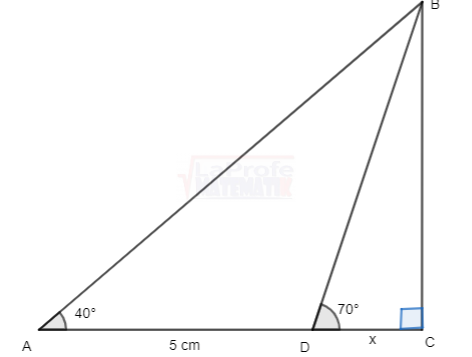Observa existen tres triángulos, en el triángulo 
se desconoce el valor del cateto adyacente 
del ángulo de 70°, entonces se aplica la razón trigonométrica de la tangente
En el triángulo 
su cateto adyacente al ángulo de 40° es el lado 
, entonces se aplica la razón de la tangente y así se relacionan el cateto del triángulo y el cateto del triángulo
Entonces se iguala los dos valores del lado 
obtenidos en ambos triángulos con el fin de determinar el valor de 
cateto adyacente del triángulo
y
El valor del cateto adyacente del triángulo es
Se calcula el cateto opuesto del triángulo , aplicando la razón trigonométrica de la tangente
Se calcula la hipotenusa del triángulo , se puede aplicar la razón trigonométrica del seno o coseno, en este caso se aplica la del seno
Calcular el ángulo del vértice B es decir 
La sumatoria interna de los ángulos de un triángulo es igual 180°
Actividades
Determina en los 6 triángulos 
los valores de las 6 razones trigonométricas
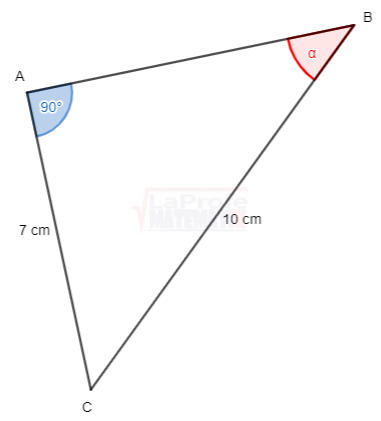
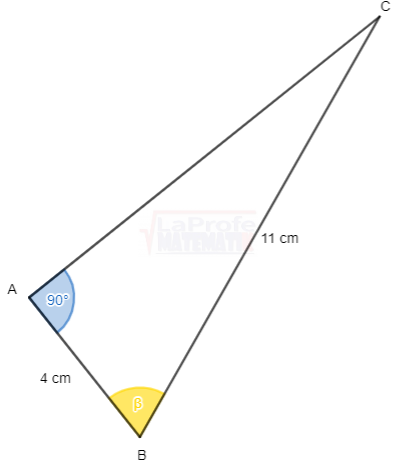
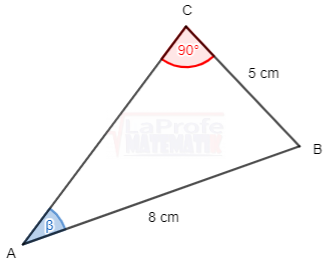
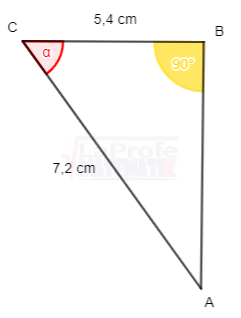
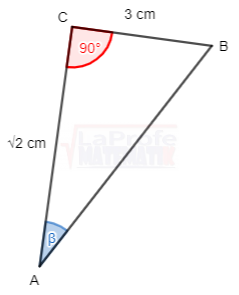
Construir un triángulo rectángulo, que cumpla con la condición dada para el ángulo β
Hallar el valor de las siguientes expresiones
Calcula las otras razones trigonométricas del ángulo θ, dado el valor de una razón en un triángulo rectángulo
Escribe la razón trigonométrica cuyo valor sea el mismo a la razón trigonométrica dado el ángulo complementario en cada caso.
Calcula las siguientes razones trigonométricas del triángulo
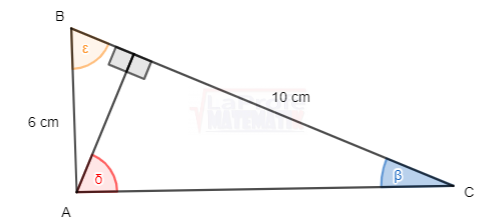
Determine aplicando el teorema de Pitágoras
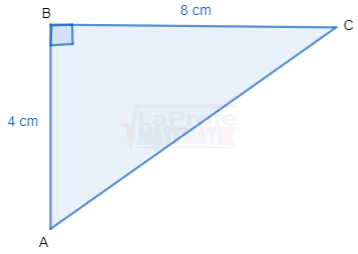
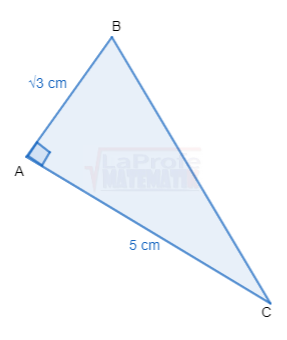
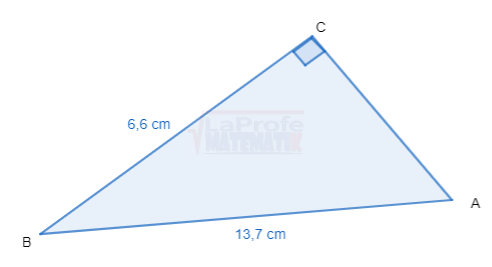
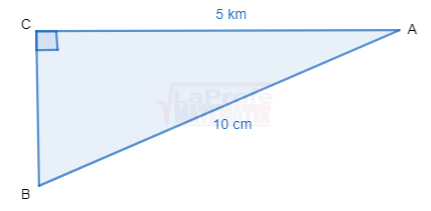Dibuja cada triángulo rectángulo y resuelve aplicando las razones trigonométricas considerando que a y b son las medidas de los catetos y c la medida de la hipotenusa
a = 6,4 cm y c = 11,7 cm
a = 4,5 cm y b = 4,5 cm
b = 7,3 cm y c = 13,6 cm
a = 12 cm y b = 10 cm
a = 2,5 cm y c = 5 cm
b = 9,6 cm y c = 14,5 cm
Determina los triángulos rectángulos
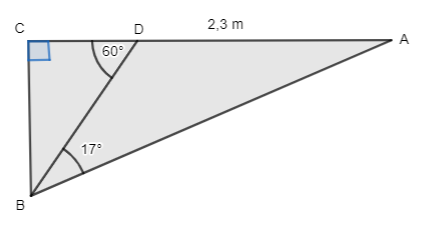
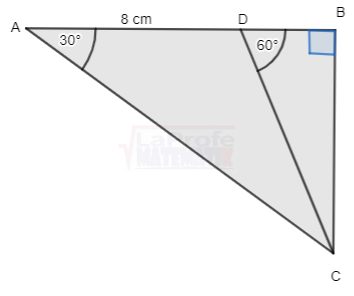
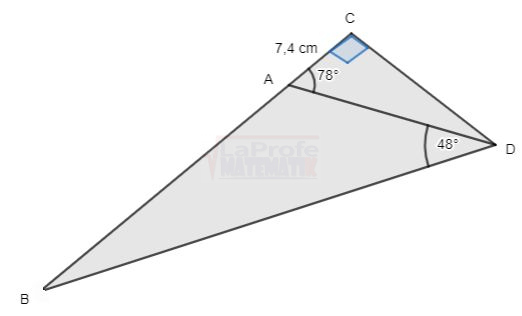
Calcula el área de los siguientes triángulos, las longitudes de los lados cada uno de ellos deben expresarse en centímetros
