 ¿Sabías que la suma y resta de monomios están presentes en problemas reales de ingeniería, economía e incluso tecnología?
¿Sabías que la suma y resta de monomios están presentes en problemas reales de ingeniería, economía e incluso tecnología?
Aprender a sumar y restar monomios no solo te ayudará a simplificar expresiones algebraicas, sino también a desarrollar el razonamiento lógico que usan los profesionales para modelar y resolver situaciones cotidianas.
Para dominar este tema, primero debes reconocer los monomios semejantes —aquellos que tienen las mismas variables y exponentes— y luego aplicar correctamente las propiedades de la potenciación.
Prepárate para descubrir lo fácil que puede ser manejar el álgebra cuando entiendes su lógica paso a paso.
Suma y resta de monomios
| Los monomios deben ser semejantes para poder sumarlos o restarlos, escribiendo siempre la misma parte literal. Todo este procedimiento es llamado reducción de términos semejantes. |
Ejemplo
 Determinar el perímetro del siguiente romboide.
Determinar el perímetro del siguiente romboide.
Para calcular el perímetro (P) de este cuadrilátero debes sumar todas las medidas de sus lados. Según la propiedad del romboide, sus lados opuestos son congruentes, es decir, poseen las mismas dimensiones.
P = 15x2y3 + 27x2y3 + 15x2y3 + 27x2y3
Se aplica factor común:
P = (15 + 27 + 15 + 27)x2y3
Finalmente se suma todos los términos
P = 84x2y3
El perímetro del romboide es 84x2y3 unidades.
Ejemplo
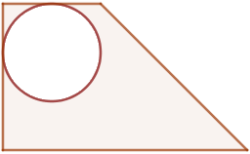 Determinar el área de la región coloreada, sabiendo que el área del trapecio rectangular es AT = 10,5 d4e6 y el área del círculo AC = 3,14 d4e6.
Determinar el área de la región coloreada, sabiendo que el área del trapecio rectangular es AT = 10,5 d4e6 y el área del círculo AC = 3,14 d4e6.
La figura está compuesta por un trapecio rectangular y un círculo, para hallar el área coloreada se requiere restar los sectores de ambas figuras.
AS = AT – AC
Se sustituye los valores del área del trapecio rectangular y el área del círculo.
AS = 10,5 d4e6 – 3,14 d4e6
Se aplica factor común:
AS = (10,5 – 3,14)d4e6
Se resta para obtener el área coloreada.
AS = 7,36 d4e6
El área coloreada es de 7,36 d4e6 unidades cuadradas.
Ejemplo#3
Calcula la suma y la resta de los siguientes monomios ![]() y
y ![]()
Al sumar:
![]()
Al restar:
![]()
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades de suma y resta de monomios
Parte I
Determina la suma de cada grupo de monomios.
-5a, 8a
-34e4, -56e4
25y, -54y, -45y
-4m2y, 17m2y, -2m2y, 6m2y
-56t5e, 65t5e, 15t5e, -10t5e, -2t5e, 20t5e, 16t5e, –t5e, 7t5e, t5e
w8, 5w8, –w8, 8w8, -5w8, 4w8, -8w8, -4w8, 0w8, -11w8, 12w8
8xzy, -18xzy, 6xzy, -13xzy, 7xzy, -3xzy, 4xzy
1.2y, 6.74y, -5.87y, -4.25y, 14.8y, -5.13y, 9y, -34y, 5y, 6.7y, y, -2y, -3y
![]()
![]()
Parte II
Calcula el área total de cada imagen teniendo en consideración el valor de las distintas zonas.
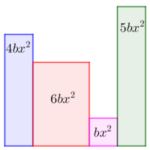
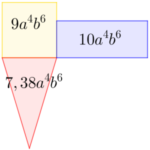
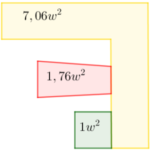
Haz uso de una expresión algebraica para que representes el perímetro de la figura.
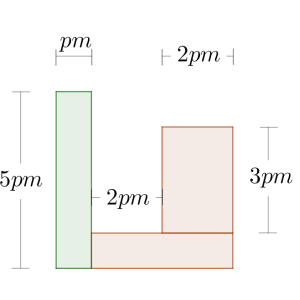
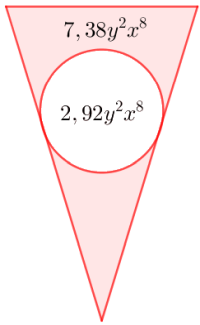
Determina el área de la parte coloreada
Parte III
Diga qué opciones son verdaderas o falsas, en caso de ser incorrecta, justifica.
- Para sumar se requiere que los monomios sean semejantes, en la resta no es necesario que se cumpla esa condición.
- La reducción de términos semejantes significa sumar o restar los coeficientes de cada monomio, y también los exponentes de cada parte literal.
- Al sumar o restar monomios no semejantes se deja indicada la operación.
Problemas:
- El perímetro de un triángulo escaleno es 18.18ab, uno de sus lados mide 8.06ab y el otro 6ab. Determina la longitud del tercero.
 El área total de la siguiente imagen es de 27m2y2. Calcula la región desconocida y selecciona la opción correcta.
El área total de la siguiente imagen es de 27m2y2. Calcula la región desconocida y selecciona la opción correcta.
Opciones:
- AT = 27m2y2 + 18m2y2 – 3m2y2
- AT = 27m2y2 – 18m2y2 + 3m2y2
- AT = 27m2y2 + (18m2y2 + 3m2y2)
- AT = 27m2y2 – (18m2y2 + 3m2y2)
Ahora que conoces un poco más acerca de la suma y resta de monomios es hora de poner en práctica lo aprendido. No olvides calificar, comentar y compartir esta información que será de gran ayuda para otros. Te invitamos a ver el artículo introducción a los polinomios. 😉

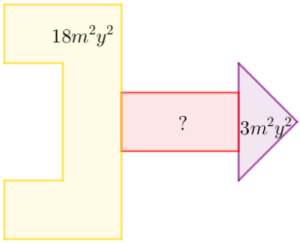 El área total de la siguiente imagen es de 27m2y2. Calcula la región desconocida y selecciona la opción correcta.
El área total de la siguiente imagen es de 27m2y2. Calcula la región desconocida y selecciona la opción correcta.
Muy buen contenido!