 ¿Sabías que las operaciones con fracciones son más comunes de lo que imaginas? No solo aparecen en los cuadernos de matemáticas: también están presentes cuando cocinas, haces compras o repartes algo entre tus amigos. Las fracciones nos ayudan a tomar decisiones con lógica y precisión.
¿Sabías que las operaciones con fracciones son más comunes de lo que imaginas? No solo aparecen en los cuadernos de matemáticas: también están presentes cuando cocinas, haces compras o repartes algo entre tus amigos. Las fracciones nos ayudan a tomar decisiones con lógica y precisión.
Imagina esta situación: Javier va a la frutería a comprar granadilla. El precio por libra es de $3.750, pero él solo tiene $2.000. ¿Qué hace? Sencillo: calcula ½ × 3.750 = 1.875. Así descubre que puede comprar media libra y aún le sobra dinero.
Este pequeño cálculo muestra cómo las operaciones con fracciones —suma, resta, multiplicación y división— no solo son parte de las clases de matemáticas, sino también herramientas útiles para la vida diaria. Si dominas estas operaciones, podrás entender mejor tu entorno, planificar tus gastos y tomar decisiones más inteligentes.
Ruta de aprendizaje para dominar las fracciones
Las fracciones pueden parecer complicadas al comienzo, y eso es completamente normal. Pero cuando se aprenden paso a paso y en el orden correcto, todo empieza a tener sentido.
En esta ruta encontrarás un camino claro que va desde lo más básico hasta las operaciones completas, para que puedas avanzar con seguridad y ganar confianza en cada tema.
¿Qué es una fracción?

Una fracción es una forma sencilla de representar una parte de un todo. Aparece cuando algo —como un objeto, una cantidad o una unidad— se divide en partes iguales y quieres expresar cuántas de esas partes se toman.
Por ejemplo, imagina una pizza cortada en 4 porciones iguales. Si comes una de ellas, has comido 1/4 de la pizza. Ese 1/4 es una fracción: el número de arriba indica cuántas partes tomas y el de abajo muestra en cuántas partes iguales se dividió el total.
Las fracciones ayudan a explicar con claridad cuánto una persona usa, comparte o cuánto le falta de algo en la vida diaria.
Partes de una fracción
Una fracción esta compuesta por dos números separados por una línea horizontal o diagonal si la expresión se escribe linealmente. A continuación, te muestro las dos formas:$$\frac{a}{b}$$
$$a/b$$
Donde:
a = Numerador.
b = Denominador.
Ejemplo:$$\frac{4}{7}$$
¿Qué significa esa fracción?
Significa que se toma 4 porciones o partes de un total dividido en 7.
¿Qué son las fracciones equivalentes?
Las fracciones equivalentes son aquellas que pueden verse distintas, pero en el fondo representan exactamente la misma cantidad.
Piensa en una barra de chocolate. Si la divides en 2 partes iguales y comes una, has comido 1/2. Ahora imagina que esa misma barra la cortas en 4 partes iguales y comes dos. En ese caso, has comido 2/4.
Aunque los números cambian, la cantidad que comiste es la misma. Por eso decimos que 1/2 y 2/4 son fracciones equivalentes.
En realidad, son diferentes maneras de expresar lo mismo. Los números se transforman, pero el valor no cambia.
Un detalle importante: podemos obtener fracciones equivalentes si multiplicamos o dividimos el numerador y el denominador por el mismo número.
Por ejemplo:
1/3 × 2/2 = 2/6
Esto nos muestra que 1/3 y 2/6 también representan la misma cantidad.
Entender las fracciones equivalentes facilita comparar, simplificar y resolver operaciones con mayor seguridad. Es como tomar rutas diferentes que, al final, te llevan al mismo destino.
¿Listo para poner a prueba lo que aprendiste?
Antes de avanzar a las operaciones con fracciones, asegúrate de dominar las fracciones equivalentes.
Esta evaluación interactiva te ayudará a detectar errores y fortalecer tu comprensión paso a paso.
👉 Haz clic y comienza ahora.
Cuestionario de fracciones equivalentes
Simplificación de fracciones
Antes de empezar a sumar, restar, multiplicar o dividir, es importante aprender a simplificar fracciones a su mínima expresión.
Para hacerlo, puedes:
- Dividir el numerador y el denominador entre un mismo número que ambos tengan en común.
- Utilizar el Máximo Común Divisor (M.C.D.) para encontrar la forma más rápida de reducirla.
Cuando una fracción está simplificada, los cálculos se vuelven más fáciles y los resultados más claros. Es como ordenar el camino antes de avanzar.
Dividir el numerador y el denominador entre un mismo número que ambos tengan en común
Para hacerlo, puedes seguir este proceso:
Primero, busca un número (preferiblemente primo) que divida exactamente tanto al numerador como al denominador.
Luego, divide ambos números entre ese mismo valor.
Si todavía pueden seguir dividiéndose entre otro número común, repite el procedimiento.
Continúa así hasta que ya no exista ningún número que los divida a los dos al mismo tiempo. En ese momento, habrás llegado a una fracción irreducible, es decir, a su forma más simple.
Ejemplo. Simplifica la siguiente expresión
$$\frac{12}{18}$$
Solución:
$$\frac{12\div 2}{18\div 2}=\frac{6\div 3}{9\div 3}=\frac{2}{3}$$
Con Máximo Común Divisor (M.C.D.)
Otra forma práctica de simplificar una fracción es utilizando el Máximo Común Divisor. Este método te permite llegar más rápido a la forma más sencilla de la fracción.
Primero, debes encontrar el M.C.D. del numerador y el denominador, es decir, el número más grande que divide exactamente a ambos.
Después, divide tanto el numerador como el denominador entre ese mismo número.
Al hacerlo, obtendrás directamente la fracción reducida a su mínima expresión, sin necesidad de dividir varias veces.
Ejemplo. Simplificar aplicando (M.C.D.)
$$\frac{144}{82}$$
Solución:
1- Descomponer en sus factores primos al numerador y denominador y aplicar M.C.D.
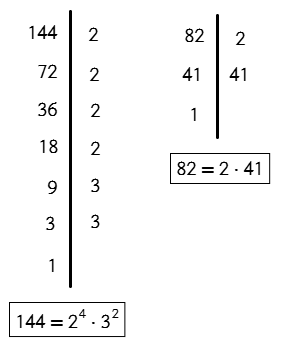
$$M.C.D.(144,82)=2$$
2- Dividir el numerador y el denominador por M.C.D.$$\frac{144\div 2}{82\div 2}=\frac{72}{41}$$
Fracción simplificada:
$$\frac{72}{41}$$
Aprende a sumar y restar fracciones con igual y diferentes denominadores
En este video vas a ver de forma clara y paso a paso cómo sumar y restar fracciones, tanto cuando tienen el mismo denominador como cuando son diferentes. Es una explicación visual que te ayudará a comprender mejor el proceso, especialmente el uso del mínimo común múltiplo para unificar denominadores.
Aprende con ejemplos simples cómo identificar denominadores iguales y distintos, cómo encontrar el mínimo común múltiplo y cómo aplicar estos pasos para sumar y restar fracciones sin errores.
Después de ver el video, a continuación encontrarás la explicación teórica desarrollada paso a paso, junto con ejemplos resueltos que te ayudarán a entender con mayor claridad cada procedimiento. Aquí reforzarás lo aprendido, resolverás posibles dudas y verás tanto el método del mínimo común múltiplo como el método cruzado explicados de forma detallada, para que puedas resolver ejercicios con seguridad y confianza.
Suma y resta de fracciones
Sumar y restar fracciones no es complicado si entiendes una idea clave: todo depende del denominador.
El denominador nos dice en cuántas partes se dividió el total. Si esas partes son iguales, la operación es más sencilla.
Cuando tienen el mismo denominador
Aquí todo es más fácil. Como las partes son del mismo tamaño, solo debes:
- Sumar o restar los numeradores.
- Dejar el mismo denominador.
- Simplificar si es posible.
Ejemplo # 1.
$$\frac{2}{5}+\frac{1}{5}=$$
Solución:
$$\frac{2}{5}+\frac{1}{5}=\frac{2+1}{5}=\frac{3}{5}$$
Ejemplo # 2.
$$\frac{2}{5}-\frac{1}{5}=$$
Solución:
$$\frac{2}{5}-\frac{1}{5}=\frac{2-1}{5}=\frac{1}{5}$$
Cuando tienen distintos denominador
Cuando las fracciones tienen denominadores diferentes, las partes no son del mismo tamaño. Y no se pueden sumar o restar partes que no son equivalentes. Primero es necesario igualarlas.
Para hacerlo, puedes usar dos métodos:
- En forma cruzada, funciona cuando solo estás trabajando con dos fracciones.
- Aplicando el Mínimo Común Múltiplo (M.C.M.), ideal cuando tienen dos o más fracciones.
Ambos métodos buscan lo mismo: convertir las fracciones en otras equivalentes que tengan el mismo denominador, para que la suma o la resta se pueda hacer correctamente.
En forma cruzada
Aplicada para operar dos fracciones.
A continuación, observa el ejemplo. Allí podrás ver el procedimiento explicado paso a paso para que entiendas cómo funciona y puedas aplicarlo con seguridad.
Sumar
$$\frac{5}{8}+\frac{15}{16}=$$
Solución:
Pasos:
1- Trazar una línea de fracción.

2- Multiplicar el numerador de la primera fracción por el denominador de la segunda fracción, el resultado ubicarlo en el numerador.
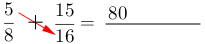
3- Escribir el signo (positivo o negativo) de la operación.
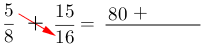
4- Multiplicar el denominador de la primera fracción por el numerador de la segunda fracción, y ubicarlo después del signo.

5- Multiplicar ambos denominadores y el resultado escribirlo como denominador.
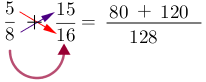
6- Escribe otra igualdad y trazar una línea de fracción.
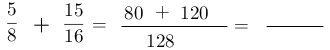
7- Operar la suma o la resta de los numeradores y escribir el resultado. En este caso se efectúa la suma.
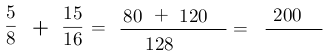
8. Escriba el mismo denominador.
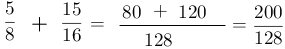
9- Sacar el Máximo Común Divisor (M.C.D). $$M.C.D. (200,128) = 8$$
10- Simplificar la fracción.
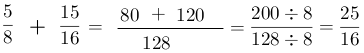
Resultado:$$\frac{25}{16}$$
Con Mínimo Común Múltiplo
Método aplicado para operaciones de sumas o restas desde dos fracciones en adelante.
La idea es encontrar un denominador común que permita convertir todas las fracciones en equivalentes con el mismo tamaño de partes. Así, la operación se vuelve mucho más clara y ordenada.
A continuación, observa el procedimiento a través de un ejemplo para entender cómo aplicarlo paso a paso.
Sumar las siguientes fracciones
$$\frac{5}{8}+\frac{15}{16}=$$
Solución:
1- Sacar el mínimo común múltiplo de los denominadores 8 y 16.$$m.c.m. (8,16) = 16$$
2- Trace una línea de fracción y en esta misma fracción escribir el resultado del m.c.m. en el denominador.
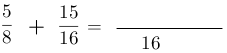
3- Dividir el denominador (m.c.m.) entre el denominador de la primera fracción, luego el resultado multiplicarlo por el numerador de la fracción, posteriormente escribirlo en el numerador de la nueva fracción.
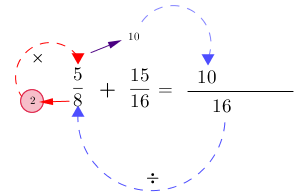
4- Escribir el signo (positivo o negativo) correspondiente. En este caso el positivo (+).
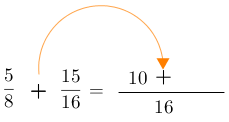
5- Repetir el mismo paso # 3 con la siguiente fracción.
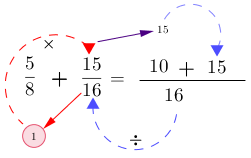
6- Sumar o restar los numeradores dejando el mismo denominador, en este caso se suma.
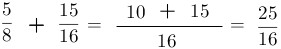
Resultado:$$\frac{25}{16}$$
Multiplicación de fracciones
Multiplicar fracciones es más sencillo de lo que parece. Solo debes multiplicar el numerador de una fracción por el numerador de la otra, y hacer lo mismo con los denominadores.
Es decir:
numerador × numerador
denominador × denominador
Después de obtener el resultado, revisa si la fracción se puede simplificar. Si es posible reducirla, hazlo para dejarla en su forma más sencilla (irreducible).
Multiplicar
$$\frac{1}{16}\times \frac{3}{128}\times \frac{5}{32}=$$
Solución:
1- Multiplique numerador con denominador y denominador con denominador.
![]()
2- La fracción obtenida es irreducible, por lo tanto el resultado es:$$\frac{15}{65 536}$$
División de fracciones
La división de fracciones puede resolverse de dos maneras: utilizando el método del inverso (multiplicar por el recíproco) o trabajando en forma cruzada. Ambas conducen al mismo resultado; lo importante es comprender el procedimiento.
A continuación, observa el ejemplo aplicando la forma cruzada para ver cómo se aplica paso a paso.
Dividir
$$\frac{13}{16}\div \frac{5}{4}=$$
Solución:
1. Multiplicar numerador de la primera fracción con el denominador de la segunda fracción.
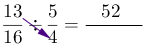
2- Multiplicar el denominador de la primera fracción con el numerador de la segunda fracción.
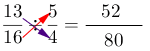
3- Sacar el M.C.D. del numerador y denominador.$$M.C.D.(52,80) = 4$$
4- Simplificar.$$\frac{52\div 4}{80\div 4}=\frac{13}{20}$$
⚠️ Errores comunes al trabajar con fracciones
Al aprender fracciones es normal cometer errores. Lo importante es identificarlos para no repetirlos. Aquí te muestro los más frecuentes:
❌ 1. Sumar o restar los denominadores
Un error muy común es hacer esto:
$$\frac{2}{3} + \frac{1}{4} = \frac{3}{7}$$
✔ Esto es incorrecto.
No se suman los denominadores.
Primero hay que buscar un denominador común y luego sumar los numeradores.
❌ 2. Restar solo los numeradores cuando los denominadores son distintos
Ejemplo incorrecto:
$$\frac{5}{6} – \frac{1}{4} = \frac{4}{6}$$
✔ Incorrecto porque los denominadores son diferentes.
Antes de restar, deben convertirse en fracciones con el mismo denominador.
❌ 3. Olvidar simplificar el resultado
Ejemplo:
$$\frac{4}{8}$$
Muchos estudiantes lo dejan así, pero puede simplificarse:
$$\frac{4}{8}=\frac{1}{2}$$
Siempre revisa si tu resultado puede simplificarse.
❌ 4. Dividir como si fuera multiplicación
Un error frecuente es intentar dividir numerador con numerador y denominador con denominador.
Por ejemplo, pensar que:
$$\frac{1}{2}\div \frac{3}{4}=\frac{1÷3}{2÷4}$$
✔ Esto es incorrecto.
En la división de fracciones no se divide cada parte por separado.
Se debe trabajar en forma cruzada: se multiplica el numerador de la primera fracción por el denominador de la segunda, y el denominador de la primera por el numerador de la segunda.
Luego, si es posible, se simplifica el resultado.
❌ 5. Cambiar solo un número al buscar fracciones equivalentes
Algunos estudiantes multiplican solo el numerador o solo el denominador.
Eso cambia el valor de la fracción.
Para obtener fracciones equivalentes, debes multiplicar o dividir ambos números por el mismo valor.
Problemas con fracciones en la vida real
Las fracciones no solo aparecen cuando el profesor lo explica en clase; también forman parte de situaciones cotidianas como cocinar, repartir comida, administrar el tiempo o calcular descuentos. A continuación encontrarás cinco problemas basados en la vida real que te ayudarán a aplicar lo aprendido y a entender cómo las fracciones se usan en situaciones concretas del día a día.
Una receta necesita 3/4 de taza de harina y tú solo tienes 1/2 taza. ¿Cuánta harina te falta para completar la receta?
Solución:
Se crea una fracción equivalente (amplificar) de 1/2 para obtener un denominador 4:
$$\frac{1}{2}=\frac{2}{4}$$
Ahora se resta:
$$\frac{3}{4}-\frac{2}{4}=\frac{1}{4}$$
Respuesta: Falta 1/4 de taza de harina.
Una pizza se divide en 8 partes iguales. Si te comes 3/8 y luego comes 2/8 más, ¿qué fracción de la pizza comiste en total?
Solución:
Sumar las fracciones porque se comieron en dos momentos:
$$\frac{3}{8}+\frac{2}{8}=\frac{5}{8}$$
Respuesta: Comiste 5/8 de la pizza.
Camila estudió 2/3 de hora por la mañana y 1/6 de hora por la tarde. ¿Cuánto tiempo estudió en total?
Solución:
$$\frac{2}{3}+\frac{1}{6}=\frac{12+3}{18}=\frac{15}{18}$$
Simplificar la fracción entre 3:
$$\frac{15}{18}=\frac{5}{6}$$
Respuesta: Camila estudió 5/6 de hora en total.
Una camiseta tiene un descuento de 1/5 de su precio. Si el precio original es $50.000, ¿cuánto dinero te descuentan?
Solución:
$$\frac{1}{5}×50.000=10.000$$
Respuesta: Te descuentan $10.000.
Un chocolate está dividido en 12 partes iguales. Si repartes 3/12 a un amigo y 4/12 a otro, ¿qué fracción del chocolate entregaste en total?
¿Te quedó más o menos de la mitad?
Solución:
$$\frac{3}{12}+\frac{4}{12}=\frac{7}{12}$$
Ahora se compara con la mitad (crear fracción equivalente):
$$\frac{1}{2}=\frac{6}{12}$$
Como:
$$\frac{7}{12}>\frac{6}{12}$$
Respuesta: Entregaste 7/12 del chocolate.
Repartiste más de la mitad.
Aplicaciones en la vida real
Las fracciones están presentes en más momentos de los que imaginamos, aunque muchas veces no nos demos cuenta.
Por ejemplo, cuando sigues una receta que indica “½ taza de azúcar”, ya estás usando una fracción. Lo mismo ocurre cuando compartes una pizza entre amigos: cada persona recibe una parte del total, es decir, una fracción.
También aparecen en áreas como la física y la geometría, donde se utilizan para medir longitudes, áreas y proporciones con mayor precisión. Y en la vida diaria son clave para calcular descuentos, impuestos o porcentajes al hacer compras.
Dominar las fracciones no solo ayuda a resolver ejercicios en el cuaderno; también fortalece el razonamiento lógico y facilita la comprensión de proporciones, razones y porcentajes. Además, son la base para temas más avanzados como el álgebra y la estadística.
¿Quieres practicar más operaciones con fracciones con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades de operaciones con fracciones
1. Determinar las siguientes sumas y restas aplicando el método cruzado y el m.c.m. Simplificar.
| a. | b. | c. | |||
| d. | e. | f. | |||
| g. | h. | i. |
2. Determinar las siguientes sumas y restas. Simplificar
| a. | b. | c. | |||
| d. | e. | f. |
3. Determinar y expresar el resultado simplificado.
| a. | b. | c. | |||
| d. | e. | f. | |||
| g. | h. | i. |
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión
