 ¿Te has preguntado alguna vez qué son realmente los polígonos y por qué los encontramos en tantas formas a nuestro alrededor?
¿Te has preguntado alguna vez qué son realmente los polígonos y por qué los encontramos en tantas formas a nuestro alrededor?
Desde la pantalla de tu celular hasta la puerta del aula, los polígonos están presentes en objetos cotidianos con formas cuadradas, rectangulares o incluso irregulares. En este post descubrirás cómo reconocerlos y comprender sus características principales.
Además, podrás interactuar con un simulador educativo que te permitirá familiarizarte con los elementos de los polígonos, explorar sus lados, ángulos y vértices, y observar cómo cambian al modificar sus figuras. ¡Prepárate para ver la geometría cobrar vida!
Polígonos
| Los polígonos son figuras planas o de dos dimensiones, formado a partir de tres segmentos en adelante, de tal forma que dos segmentos quedan unidos en un punto y cada segmento se ubica exactamente a otros dos segmentos. |
Elementos de los polígonos
Son cinco y se llaman:
1.Lados.
2.Vértices.
3.Ángulos internos.
4.Ángulos externos
5.Diagonales.

Conceptos
A continuación, los conceptos de cada uno de ellos.
Lados
| Son los segmentos del polígono. Cuando se dibuja o se traza un lado y luego el otro, ambos lados se les da el nombre de lados consecutivos. |
Vértices
| Son los puntos que unen dos lados consecutivos del polígono. |
Ángulos internos
| Son aquellos que se ubican entre dos lados consecutivos del polígono. |
Ángulos externos
| Son los ángulos suplementarios a los ángulos internos. |
Diagonales
| Son segmentos que unen dos vértices no consecutivos. |
Cálculo de las diagonales por vértice
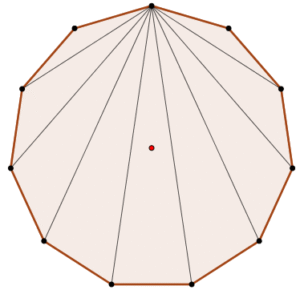 Se puede determinar a través de la siguiente fórmula:
Se puede determinar a través de la siguiente fórmula:
![]()
Cálculo del total de diagonales del polígono
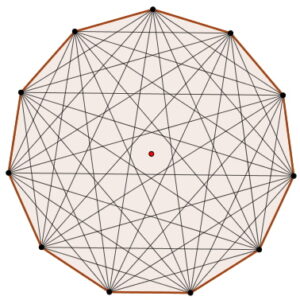 Para calcular el total de diagonales se debe aplicar la siguiente relación:
Para calcular el total de diagonales se debe aplicar la siguiente relación:
![]()
Clasificación de los polígonos
Los polígonos se clasifican según:
1.Cantidad de lados.
2.Medida de sus ángulos internos y de sus lados.
3.Tipo de convexidad.
Cantidad de lados
Según la cantidad de lados el polígono tiene establecido un nombre, a continuación los nombres de algunos de ellos:
| Nombre | Lados |
| Triángulo | 3 |
| Cuadrilátero | 4 |
| Pentágono | 5 |
| Hexágono | 6 |
| Heptágono | 7 |
| Octágono | 8 |
| Eneágono | 9 |
| Decágono | 10 |
| Undecágono | 11 |
| Dodecágono | 12 |
| Pentadecágono | 15 |
| Icoságono | 20 |
Juega con los cuadriláteros
¿Sabías que con solo mover algunos vértices puedes descubrir qué hace únicos a los cuadriláteros?
En esta simulación interactiva podrás explorar las propiedades de figuras como el cuadrado, el rombo, el trapecio y el paralelogramo, observando cómo cambian sus lados y ángulos. Es una forma divertida y visual de comprender las características geométricas que diferencian cada figura.
Medida de sus ángulos internos y de sus lados
Cuando todas las medidas de los ángulos internos de un polígono son iguales, todas las medidas de sus lados también lo es. Por lo tanto recibe el nombre de polígono regular.
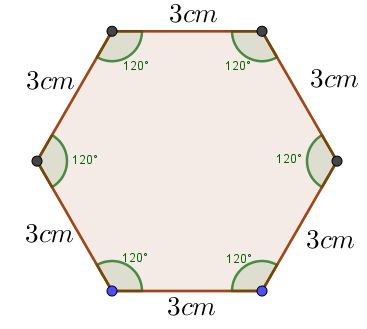
Pero cuando al menos la medida de uno de sus ángulos internos o uno de sus lados es distinto a todos, es llamado polígono irregular.
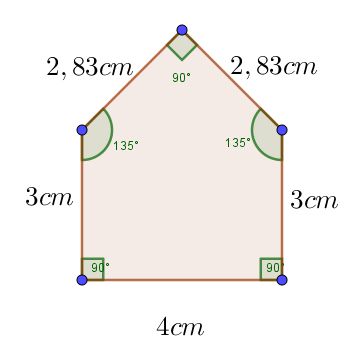
Tipo de convexidad
Existen dos tipos de polígonos según su convexidad y son llamados:
- Convexos y
- Cóncavos.
Un polígono convexo es cuando las medidas de todos sus ángulos internos son menores a 180°.

Un polígono cóncavo es cuando existe algún ángulo interno mayor de 180°

¿Sabes el nombre que le darás al polígono de “n” lados?
¿Qué sucedería si en algún momento te piden el nombre de un polígono de 123 lados? ¿lo respondería con facilidad?.
Para darle el nombre a un polígono debes estar segur construirlo, y para poder realizarlo lo primero es aprender la técnica para que puedas dar el nombre de cualquier polígono. Aquí se comenzará desde las unidades (1 hasta el 9), las decenas
Nombres de polígonos 3 a 9 lados
La fórmula es unir:
Unidades + gono
| Lados | Unidades | Indicador de polígono | Escritura |
|---|---|---|---|
| 3 | Trí | gono | Trígono |
| 4 | Tetrá | gono | Tetrágono |
| 5 | Pentá | gono | Pentágono |
| 6 | Hexá | gono | Hexágono |
| 7 | Heptá | gono | Heptágono |
| 8 | Octá / Octó | gono | Octágono |
| 9 | Eneá / Nona | gono | Eneágono |
Existen polígonos que comúnmente se conocen con el nombre de triángulos y cuadrados, pero su nombre real según la fórmula es: trígono y tetrágono respectivamente.
Nombres de polígonos 10 a 19 lados
La fórmula es unir:
Unidades + Decá + gono
| Lado | Unidades | Primera decena | Indicador de polígono | Escritura |
|---|---|---|---|---|
| 10 | – | Decá | gono | Decágono |
| 11 | En | Decá | gono | Endecágono |
| 12 | Do | Decá | gono | Dodecágono |
| 13 | Tri | Decá | gono | Tridecágono |
| 14 | Tetra | Decá | gono | Tetradecágono |
| 15 | Penta | Decá | gono | Pentadecágono |
| 16 | Hexa | Decá | gono | Hexadecágono |
| 17 | Hepta | Decá | gono | Heptadecágono |
| 18 | Octa | Decá | gono | Octadecágono |
| 19 | Enea | Decá | gono | Eneadecágono |
Nombres de polígonos 20 a 29 lados
A partir de aquí se usa la siguiente fórmula:
Decena + kai + Unidades + gono
| Lado | Segunda decena | Conjunción | Unidades | Indicador de polígono | Escritura |
|---|---|---|---|---|---|
| 20 | Icosa | – | – | gono | Icosagono |
| 21 | Icosa | kai | Hená | gono | Icosakaihenagono |
| 22 | Icosa | kai | Dí | gono | Icosakaidigono |
| 23 | Icosa | kai | Trí | gono | Icosakaitrígono |
| 24 | Icosa | kai | Tetrá | gono | Icosakaitetrágono |
| 25 | Icosa | kai | Pentá | gono | Icosakaipentágono |
| 26 | Icosa | kai | Hexá | gono | Icosakaihexágono |
| 27 | Icosa | kai | Heptá | gono | Icosakaiheptágono |
| 28 | Icosa | kai | Octá | gono | Icosakaioctágono |
| 29 | Icosa | kai | Eneá | gono | Icosakaieneágono |
Nombres de polígonos 30 a 39 lados
Fórmula:
Decena + kai + Unidades + gono
| Lado | Tercera decena | Conjunción | Unidades | Indicador de polígono | Escritura |
|---|---|---|---|---|---|
| 30 | Triaconta | – | – | gono | Triacontagono |
| 31 | Triaconta | kai | Hená | gono | Triacontakaihenagono |
| 32 | Triaconta | kai | Dí | gono | Triacontakaidigono |
| 33 | Triaconta | kai | Trí | gono | Triacontakaitrígono |
| 34 | Triaconta | kai | Tetrá | gono | Triacontakaitetrágono |
| 35 | Triaconta | kai | Pentá | gono | Triacontakaipentágono |
| 36 | Triaconta | kai | Hexá | gono | Triacontakaihexágono |
| 37 | Triaconta | kai | Heptá | gono | Triacontakaiheptágono |
| 38 | Triaconta | kai | Octá | gono | Triacontakaioctágono |
| 39 | Triaconta | kai | Eneá | gono | Triacontakaieneágono |
Nombres de polígonos 40 a 49 lados
Fórmula:
Decena + kai + Unidades + gono
| Lado | Cuarta decena | Conjunción | Unidades | Indicador de polígono | Escritura |
|---|---|---|---|---|---|
| 40 | Tetraconta | – | – | gono | Tetracontagono |
| 41 | Tetraconta | kai | Hená | gono | Tetracontakaihenagono |
| 42 | Tetraconta | kai | Dí | gono | Tetracontakaidigono |
| 43 | Tetraconta | kai | Trí | gono | Tetracontakaitrígono |
| 44 | Tetraconta | kai | Tetrá | gono | Tetracontakaitetrágono |
| 45 | Tetraconta | kai | Pentá | gono | Tetracontakaipentágono |
| 46 | Tetraconta | kai | Hexá | gono | Tetracontakaihexágono |
| 47 | Tetraconta | kai | Heptá | gono | Tetracontakaiheptágono |
| 48 | Tetraconta | kai | Octá | gono | Tetracontakaioctágono |
| 49 | Tetraconta | kai | Eneá | gono | Tetracontakaieneágono |
Nombres de polígonos 50 a 59 lados
Fórmula:
Decena + kai + Unidades + gono
| Lado | Quinta decena | Conjunción | Unidades | Indicador de polígono | Escritura |
|---|---|---|---|---|---|
| 50 | Pentaconta | – | – | gono | Pentacontagono |
| 51 | Pentaconta | kai | Hená | gono | Pentacontakaihenágono |
| 52 | Pentaconta | kai | Dí | gono | Pentacontakaidígono |
| 53 | Pentaconta | kai | Trí | gono | Pentacontakaitrígono |
| 54 | Pentaconta | kai | Tetrá | gono | Pentacontakaitetrágono |
| 55 | Pentaconta | kai | Pentá | gono | Pentacontakaipentágono |
| 56 | Pentaconta | kai | Hexá | gono | Pentacontakaihexágono |
| 57 | Pentaconta | kai | Heptá | gono | Pentacontakaiheptágono |
| 58 | Pentaconta | kai | Octá | gono | Pentacontakaioctágono |
| 59 | Pentaconta | kai | Eneá | gono | Pentacontakaieneágono |
Nombres de polígonos 60 a 69 lados
Fórmula:
Decena + kai + Unidades + gono
| Lado | Sexta decena | Conjunción | Unidades | Indicador de polígono | Escritura |
|---|---|---|---|---|---|
| 60 | Hexaconta | – | – | gono | Hexacontagono |
| 61 | Hexaconta | kai | Hená | gono | Hexacontakaihenágono |
| 62 | Hexaconta | kai | Dí | gono | Hexacontakaidígono |
| 63 | Hexaconta | kai | Trí | gono | Hexacontakaitrígono |
| 64 | Hexaconta | kai | Tetrá | gono | Hexacontakaitetrágono |
| 65 | Hexaconta | kai | Pentá | gono | Hexacontakaipentágono |
| 66 | Hexaconta | kai | Hexá | gono | Hexacontakaihexágono |
| 67 | Hexaconta | kai | Heptá | gono | Hexacontakaiheptágono |
| 68 | Hexaconta | kai | Octá | gono | Hexacontakaioctágono |
| 69 | Hexaconta | kai | Eneá | gono | Hexacontakaieneágono |
Nombres de polígonos 70 a 79 lados
Fórmula:
Decena + kai + Unidades + gono
| Lado | Séptima decena | Conjunción | Unidades | Indicador de polígono | Escritura |
|---|---|---|---|---|---|
| 70 | Heptaconta | – | – | gono | Heptacontagono |
| 71 | Heptaconta | kai | Hená | gono | Heptacontakaihenágono |
| 72 | Heptaconta | kai | Dí | gono | Heptacontakaidígono |
| 73 | Heptaconta | kai | Trí | gono | Heptacontakaitrígono |
| 74 | Heptaconta | kai | Tetrá | gono | Heptacontakaitetrágono |
| 75 | Heptaconta | kai | Pentá | gono | Heptacontakaipentágono |
| 76 | Heptaconta | kai | Hexá | gono | Heptacontakaihexágono |
| 77 | Heptaconta | kai | Heptá | gono | Heptacontakaiheptágono |
| 78 | Heptaconta | kai | Octá | gono | Heptacontakaioctágono |
| 79 | Heptaconta | kai | Eneá | gono | Heptacontakaieneágono |
Nombres de polígonos 80 a 89 lados
Fórmula:
Decena + kai + Unidades + gono
| Lado | Octava decena | Conjunción | Unidades | Indicador de polígono | Escritura |
|---|---|---|---|---|---|
| 80 | Octaconta | – | – | gono | Octacontagono |
| 81 | Octaconta | kai | Hená | gono | Octacontakaihenágono |
| 82 | Octaconta | kai | Dí | gono | Octacontakaidígono |
| 83 | Octaconta | kai | Trí | gono | Octacontakaitrígono |
| 84 | Octaconta | kai | Tetrá | gono | Octacontakaitetrágono |
| 85 | Octaconta | kai | Pentá | gono | Octacontakaipentágono |
| 86 | Octaconta | kai | Hexá | gono | Octacontakaihexágono |
| 87 | Octaconta | kai | Heptá | gono | Octacontakaiheptágono |
| 88 | Octaconta | kai | Octá | gono | Octacontakaioctágono |
| 89 | Octaconta | kai | Eneá | gono | Octacontakaieneágono |
Nombres de polígonos 90 a 99 lados
Fórmula:
Decena + kai + Unidades + gono
| Lado | Novena decena | Conjunción | Unidades | Indicador de polígono | Escritura |
|---|---|---|---|---|---|
| 90 | Eneaconta | – | – | gono | Eneacontagono |
| 91 | Eneaconta | kai | Hená | gono | Eneacontakaihenágono |
| 92 | Eneaconta | kai | Dí | gono | Eneacontakaidígono |
| 93 | Eneaconta | kai | Trí | gono | Eneacontakaitrígono |
| 94 | Eneaconta | kai | Tetrá | gono | Eneacontakaitetrágono |
| 95 | Eneaconta | kai | Pentá | gono | Eneacontakaipentágono |
| 96 | Eneaconta | kai | Hexá | gono | Eneacontakaihexágono |
| 97 | Eneaconta | kai | Heptá | gono | Eneacontakaiheptágono |
| 98 | Eneaconta | kai | Octá | gono | Eneacontakaioctágono |
| 99 | Eneaconta | kai | Eneá | gono | Eneacontakaieneágono |
Nombres de polígonos 100 a 999 lados
La fórmula es la misma:
Centena + gono
Con unidades y decenas, la fórmula es la siguiente:
Centena + decena + kai + unidades + gono
| Lado | Centena | Indicador de polígono | Escritura |
|---|---|---|---|
| 100 | Hectá | gono | Hectágono |
| 200 | Dohectá | gono | Dohectágono |
| 300 | Trihectá | gono | Trihectágono |
| 400 | Tetrahectá | gono | Tetrahectágono |
| 500 | Pentahectá | gono | Pentahectágono |
| 600 | Hexahectá | gono | Hexahectágono |
| 700 | Heptahectá | gono | Heptahectágono |
| 800 | Octahectá | gono | Octahectágono |
| 900 | Eneahectá | gono | Eneahectágono |
Otras decenas
| Lado | Centena | Decena | y | Unidades | Indicador de polígono | Escritura |
|---|---|---|---|---|---|---|
| 123 | Hectá | icosa | kai | tri | gono | Hectáicosakaitrigono |
| 278 | Dohectá | heptaconta | kai | octa | gono | Dohectáheptacontakaioctagono |
| 435 | Tetrahectá | triaconta | kai | penta | gono | Tetrahectátriacontakaipentagono |
| 756 | Heptahectá | pentaconta | kai | hexa | gono | Heptahectápentacontakaihexagono |
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
Completa la tabla

Observa la siguiente imagen y responde cada pregunta

- ¿Qué cantidad de vértices tiene la figura?
- Escriba cada vértice
- ¿Cuántos lados tiene?
- Escriba cada lado
- ¿Cuántas diagonales tiene?
- Diga el nombre del polígono según el número de lados.
- Mencione el tipo de polígono según el tipo de convexidad
- Tipo de polígono según las medidas de sus lados
Determina por medio de la fórmula la cantidad de diagonales de cada uno de los siguientes polígonos.
- Eneágono.
- Pentadecágono.
- Tetradecágono o cuadrilátero.
- Icoságono.
- Triaconta.
La figura a continuación es un dodecágono regular, el número de diagonales que tiene es:

- Igual a 12.
- Igual a 6.
- Mayor que 12.
- Menor que 6.
Si te gustó este contenido, comparte con tus amigos 😉 seguramente será de gran ayuda para ellos. También nos encantaría leer tus comentarios acerca de este tema. No olvides que si necesitas refuerzo en este tema puedes contactarnos, con gusto te agendaremos una clase.

Hola, me gusta este contenido. Gracias.