¿Te complican los ángulos mayores a 90°? 📐 ¡Hay una forma sencilla de dominarlos!

5/5 - (1 voto)

¿Quieres aprender a dominar tus videojuegos favoritos sabiendo cómo reducir ángulos al primer cuadrante? Imagina que tienes que hacer un lanzamiento perfecto, pero el objetivo está en un ángulo de 300°. En lugar de memorizar todos los valores para cada ángulo, existe un «truco» matemático que simplifica ese 300° a un ángulo mucho más fácil de manejar: 60°. Con esta técnica, podrás descifrar cualquier ángulo, sin importar qué tan grande sea, ¡y subir de nivel en tus habilidades de cálculo!

Contenido del tema

Signos de las funciones trigonométricas

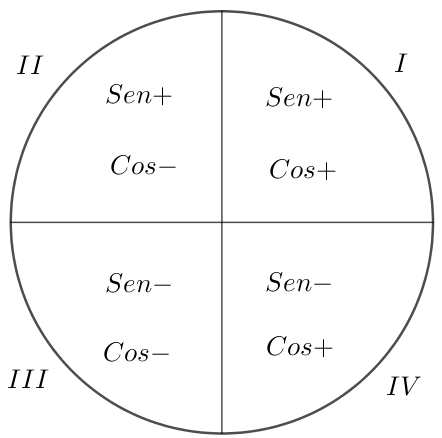
Según el cuadrante donde se ubique el ángulo las funciones trigonométricas puede ser positivas o negativas, por ejemplo si el ángulo es 150° este está ubicado en el segundo cuadrante por lo tanto la función trigonométrica del seno de 150° es positivo y la función trigonométrica del coseno de 150° es negativo.

$$\sin 150^{\circ} = \frac{1}{2}$$

$$\cos 150^{\circ} = -\frac{\sqrt{3}}{2}$$

Para los signos de la tangente debes dividir el signo del seno entre el signo del coseno.

Los signos de las funciones inversas son los mismos signos de sus funciones directas.

Cómo obtener los valores de las funciones trigonométricas sin calculadora

Para obtener los valores de las funciones trigonométricas (ejemplo: sin150°=1/2) de ángulos notables (30°, 45°, 60°, 120°, 135°, 150°, 210°, 225°, 240°, 300°, 315°, 330°) no hace falta que utilices la calculadora, solo debes hacer uso del siguiente truco matemático, observa la imagen: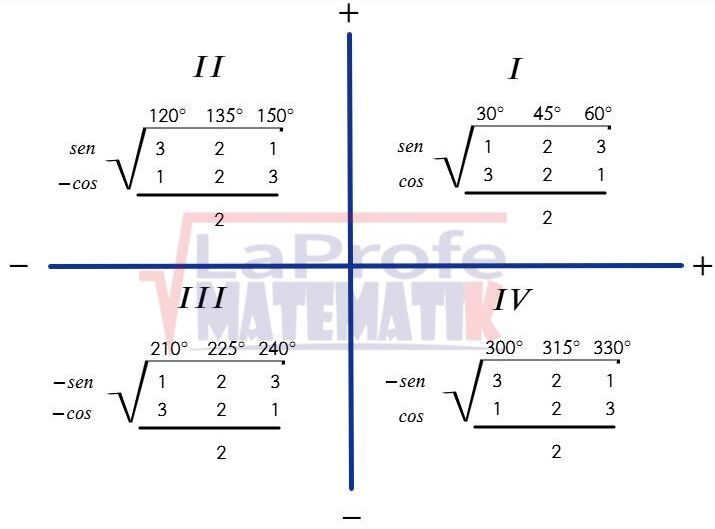

Ejemplo # 1. Determine sen30°

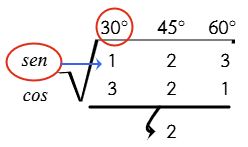
Resultado: $$sen30^{\circ }=\frac{{1}}{2}$$

Ejemplo # 2. Calcular cos210°

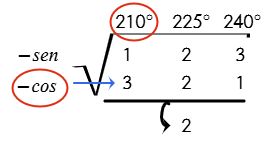
Resultado: $$cos210^{\circ }=-\frac{\sqrt{3}}{2}$$

Para conseguir los valores de la función tangente debes aplicar la razón trigonométrica:

$$tan\alpha=\frac{sen\alpha }{cos\alpha }$$

Por ejemplo, hallar el valor de la tan150°

$$tan150^{\circ }=\frac{\frac{1}{2} }{-\frac{\sqrt{3}}{2} }$$

$$tan150^{\circ }=-\frac{\sqrt{3}}{3}$$

Fórmulas para convertir ángulos del IV,III,II al I cuadrante

¿Cómo reducir ángulos al primer cuadrante? No te preocupes, a continuación, te muestro tres fórmulas sencillas que son el atajo que estabas buscando. Con ellas, podrás convertir de manera rápida y sin complicaciones cualquier ángulo del segundo, tercer o cuarto cuadrante a su valor equivalente en el primer cuadrante. Dominar esta herramienta es clave para simplificar tus cálculos y resolver cualquier problema de trigonometría.

	Cuadrante	Fórmula
1	II al I	$$\alpha = 180^{\circ} – \beta$$
2	III al I	$$\alpha = \beta – 180^{\circ}$$
3	IV al I	$$\alpha = 360^{\circ} – \beta$$

Caso#1: Convertir ángulos del II cuadrante al I cuadrante

Ejemplo#1: Convertir el ángulo 120° al primer cuadrante y determinar todas las funciones trigonométricas y sus inversas

Solución#1:

Identificar el cuadrante del ángulo, en este caso el ángulo 120° se encuentra en el cuadrante II
Seleccionar la fórmula, por estar el ángulo (120°) en el II cuadrante se aplica la primera fórmula: $$\alpha = 180^{\circ} – \beta$$
Cálculo del ángulo en el primer cuadrante, se sustituye el valor del ángulo 120° en la fórmula: $$\alpha = 180^{\circ} – 120^{\circ} = 60^{\circ}$$
Ángulo coterminal = 60°

Solución#2:

Determinar todas las funciones trigonométricas. El ángulo de 120° es del II cuadrante por lo tanto el resultado de los signos de las funciones trigonométricas del seno es +, del coseno es -, y el de la tangente es -, y los signos de sus inversas son los mismos.

$$\sin 120^{\circ} = \sin 60^{\circ} = \frac{\sqrt{3}}{2}$$

$$\cos 120^{\circ} = -\cos 60^{\circ} = -\frac{1}{2}$$

$$\tan 120^{\circ} = -\tan 60^{\circ} = -\sqrt{3}$$

$$\csc 120^{\circ} = \csc 60^{\circ} = \frac{2}{\sqrt{3}}$$

Por estar el radical en el denominador se racionaliza y su procedimiento es el siguiente:

$$\csc 120^{\circ} = \csc 60^{\circ} =$$
$$ =\frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{2\sqrt{3}}{(\sqrt{3})^{2}} = \frac{2\sqrt{3}}{3}$$

$$\sec 120^{\circ} = -\sec 60^{\circ} = -2$$

$$\cot 120^{\circ} = -\cot 60^{\circ} = -\frac{\sqrt{3}}{3}$$

Caso#2: Convertir ángulos del III cuadrante al I cuadrante

Ejemplo#2: Convertir el ángulo 225° al primer cuadrante y determinar todas las funciones trigonométricas e inversas.

Solución#1:

Identificar el cuadrante del ángulo, el ángulo 225° se encuentra en el III cuadrante
Seleccionar la fórmula, se aplica la segunda fórmula $\alpha = \beta - 180^{\circ}$
Cálculo del ángulo, se sustituye el valor del ángulo 225° en la fórmula: $$\alpha = 225^{\circ} – 180^{\circ} = 45^{\circ}$$
Ángulo coterminal = 45°

Solución#2:

Determinar todas las funciones trigonométricas tomando en cuenta sus signos en el III cuadrante

$$\sin 225^{\circ} = -\sin 45^{\circ} = -\frac{\sqrt{2}}{2}$$

$$\cos 225^{\circ} = -\cos 45^{\circ} = -\frac{\sqrt{2}}{2}$$

$$\tan 225^{\circ} = \tan 45^{\circ} = 1$$

$$\csc 225^{\circ} = -\csc 45^{\circ} = $$
$$=-\frac{1}{\frac{\sqrt{2}}{2}} = -\frac{2}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = -\sqrt{2}$$

$$\sec 225^{\circ} = -\sec 45^{\circ} =$$
$$= -\frac{1}{\frac{\sqrt{2}}{2}} = -\frac{2}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = -\sqrt{2}$$

$$\cot 225^{\circ} = \cot 45^{\circ} = 1$$

Caso#3: Convertir ángulos del IV cuadrante al I cuadrante

Ejemplo#3: Convertir el ángulo 330° al primer cuadrante y determinar todas las funciones trigonométricas e inversas

Solución#1:

Identificar el cuadrante del ángulo, el ángulo 330° se encuentra en el IV cuadrante
Seleccionar la fórmula, se aplica la tercera fórmula $\alpha = 360^{\circ} - \beta$
Cálculo del ángulo, sustituir el valor del ángulo 330° en la fórmula: $$\alpha = 360^{\circ} – 330^{\circ} = 30^{\circ}$$
Ángulo coterminal = 30°

Solución#2:

Determinar todas las funciones trigonométricas tomando en cuenta sus signos en el IV cuadrante

$$\sin 330^{\circ} = -\sin 30^{\circ} = -\frac{1}{2}$$

$$\cos 330^{\circ} = \cos 30^{\circ} = \frac{\sqrt{3}}{2}$$

$$\tan 330^{\circ} = -\tan 30^{\circ} = -\frac{\sqrt{3}}{3}$$

$$\csc 330^{\circ} = -\csc 30^{\circ} = -\frac{1}{\frac{1}{2}} = -2$$

$$\sec 330^{\circ} = \sec 30^{\circ} =$$
$$= \frac{1}{\frac{\sqrt{3}}{2}} = \frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{2\sqrt{3}}{3}$$

$$\cot 330^{\circ} = -\cot 30^{\circ} =$$
$$= -\frac{1}{\frac{\sqrt{3}}{3}} = -\frac{3}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = -\sqrt{3}$$

Caso#4: Convertir ángulos mayores de 360° al I cuadrante

Cuando son ángulos mayores de 360° se realiza una división de ese ángulo entre 360° y se escoge el residuo.

Ejemplo#4: Determine el valor del seno de 2025°

Para determinar la reducción de este ángulo al I cuadrante debes cumplir con los siguientes pasos:

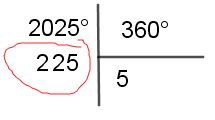
Dividir el ángulo 2025° entre 360°, se toma el resto como ángulo reducido
El ángulo 225° está en el III cuadrante, se aplica todos los 4 pasos de los casos anteriores para obtener el ángulo coterminal en el I cuadrante
$\alpha = 225^{\circ} - 180^{\circ} = 45^{\circ}$