 Resolver triángulos rectángulos es una de las habilidades más importantes dentro de la geometría y la trigonometría. Este conocimiento permite calcular alturas, distancias y longitudes que no pueden medirse directamente. Por ejemplo, se utiliza para determinar la altura de un edificio, la distancia entre dos puntos inaccesibles o la inclinación de una rampa.
Resolver triángulos rectángulos es una de las habilidades más importantes dentro de la geometría y la trigonometría. Este conocimiento permite calcular alturas, distancias y longitudes que no pueden medirse directamente. Por ejemplo, se utiliza para determinar la altura de un edificio, la distancia entre dos puntos inaccesibles o la inclinación de una rampa.
Dominar este procedimiento no solo es fundamental en matemáticas, sino también en áreas como la física, la ingeniería, la arquitectura y el diseño digital. En esta guía se explica paso a paso cómo resolver triángulos rectángulos utilizando el teorema de Pitágoras y las razones trigonométricas, con ejemplos claros y aplicables.
Qué es un triángulo rectángulo
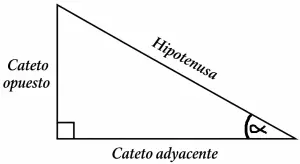 Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90°.
Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90°.
Este tipo de triángulo posee tres lados fundamentales:
- Hipotenusa
- Cateto opuesto
- Cateto adyacente
Estos elementos forman la base para definir las razones trigonométricas y resolver una gran variedad de problemas geométricos.
Elementos de un triángulo rectángulo
Hipotenusa
Es el lado más largo del triángulo y siempre se encuentra opuesto al ángulo recto.
Se representa comúnmente con la letra: h
Cateto opuesto
Es el lado que se encuentra frente al ángulo de referencia.
Se representa como: co
Cateto adyacente
Es el lado que se encuentra junto al ángulo de referencia.
Se representa como: ca
Fórmulas para resolver triángulos rectángulos
Existen dos herramientas principales.
1. Teorema de Pitágoras
Se utiliza cuando se conocen dos lados y se desea encontrar el tercero.
$$h^{2}=co^{2}+ca^{2}$$
2. Razones trigonométricas
Se utilizan cuando se conoce un ángulo agudo y uno de los lados del triángulo.
Seno:
$$sen\beta =\frac{co}{h}$$
Coseno:
$$cos\beta =\frac{ca}{h}$$
Tangente:
$$tan\beta =\frac{co}{ca}$$
Cómo resolver un triángulo rectángulo paso a paso
Para resolver correctamente un triángulo rectángulo, se recomienda seguir este procedimiento:
1. Identificar los datos conocidos.
2. Identificar la incógnita.
3. Seleccionar la fórmula adecuada.
4. Sustituir los valores.
5. Realizar los cálculos.
6. Verificar el resultado obtenido.
Este proceso garantiza una solución ordenada y precisa.
Ejercicios resueltos paso a paso
Los ejercicios resueltos permiten comprender el procedimiento completo y desarrollar la capacidad de resolver problemas de forma independiente. Cuando el estudiante entiende el proceso, puede aplicar el mismo método en nuevas situaciones con mayor confianza.
Problema 1 (nivel básico)
Calcular el valor de x
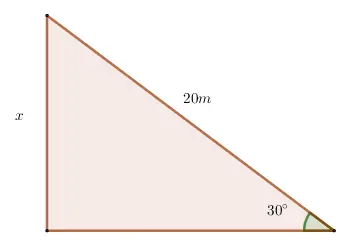
Solución:
Como x es el cateto opuesto y se conoce la hipotenusa, se utiliza la razón seno:
$$sen\beta =\frac{co}{h}\Rightarrow co=h\cdot sen\beta $$
Despejando:
$$co=h\cdot sen\beta$$
Sustituyendo:
$$co=20m\cdot sen30^{\circ}$$
$$co=20m\cdot \frac{1}{2}$$
Resultado:
$$ \boxed{co=10m}$$
Problema 2 (nivel intermedio)
Determinar los lados desconocidos del triángulo.
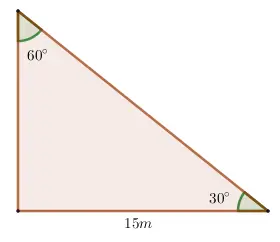
Solución:
Paso 1: Calcular la hipotenusa
Se aplica la razón seno de 60° y se despeja:
$$sen60^{\circ} =\frac{co}{h}\Rightarrow h=\frac{co}{sen60^{\circ}} $$
$$h=\frac{co}{sen60^{\circ}}$$
Sustituyendo:
$$h=\frac{15m}{\frac{\sqrt{3}}{2}}$$
Racionalizando:
$$h=\frac{30}{\sqrt{3}}\cdot\frac{\sqrt{3}}{\sqrt{3}}=\frac{30\sqrt{3}}{3}$$
$$\boxed{h=10\sqrt{3}m}$$
Paso 2: Calcular el cateto opuesto.
Aplicando seno de 30°.
$$sen30^{\circ}=\frac{co}{10\sqrt{3}}$$
Despejando y sustituyendo valores:
$$co=10\sqrt{3}\cdot \frac{1}{2}$$
Resultado:
$$ \boxed{co=5\sqrt{3}m}$$
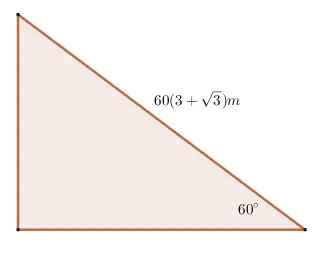
Problema 3 (nivel avanzado)
Calcular el perímetro y el área del triángulo.
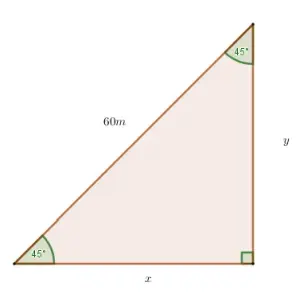
Solución:
Paso 1: Calcular el cateto opuesto
$$sen45^{\circ}=\frac{co}{h}\Rightarrow co=h\cdot sen45^{\circ}$$
$$co=60m\cdot \frac{\sqrt{2}}{2}$$
$$ \boxed{co=30\sqrt{2}m}$$
Paso 2: Calcular el cateto adyacente
$$tan45^{\circ}=\frac{co}{ca}\Rightarrow ca=\frac{co}{tan45^{\circ}}$$
$$ca=\frac{30\sqrt{2}m}{1}$$
$$ \boxed{ca=30\sqrt{2}m}$$
Paso 3: Calcular el perímetro
$$P=h+co+ca$$
$$P=60m+30\sqrt{2}m+30\sqrt{2}m$$
$$P=60+60\sqrt{2}m$$
Se factoriza y el perímetro es:
$$ \boxed{P=60(\sqrt{2}+1)}$$
Paso 4: Calcular el área
$$A_{\bigtriangleup }=\frac{b.h}{2}=\frac{ca\cdot co}{2}$$
Sustitución de valores:
$$A_{\bigtriangleup }=\frac{30\sqrt{2}m\cdot 30\sqrt{2}m}{2}$$
Multiplicación de los dos factores:
$$A_{\bigtriangleup }=\frac{\left ( 30\sqrt{2}m \right )^{2}}{2}$$
Aplicación de potencias:
$$A_{\bigtriangleup }=\frac{900m^{2}\cdot 2}{2}$$
Resultado:
$$\boxed{A_{\bigtriangleup }=900m^{2}}$$
Errores comunes al resolver triángulos rectángulos
Reconocer estos errores permite evitarlos y mejorar la precisión.
1: Confundir cateto opuesto y adyacente.
2: Utilizar una razón trigonométrica incorrecta.
3: No identificar correctamente el ángulo de referencia.
4: Usar la calculadora en modo incorrecto (grados en lugar de radianes o viceversa).
5: Aplicar incorrectamente el teorema de Pitágoras.
¿Para qué sirve resolver triángulos rectángulos?
Resolver triángulos rectángulos tiene aplicaciones reales en múltiples áreas. Se utiliza en arquitectura para calcular alturas, en ingeniería para medir distancias, en física para analizar fuerzas y en desarrollo de videojuegos para calcular posiciones y movimientos.
Además, este proceso fortalece el pensamiento lógico. El estudiante aprende a analizar información, seleccionar una estrategia y resolver problemas de forma estructurada. Esta habilidad es útil no solo en matemáticas, sino en cualquier situación que requiera razonamiento y toma de decisiones.
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
Resuelve cada ejercicio utilizando razones trigonométricas para determinar el triángulo rectángulo y simplifica los resultados mediante racionalización y factorización.
1. Determinar la altura del triángulo.
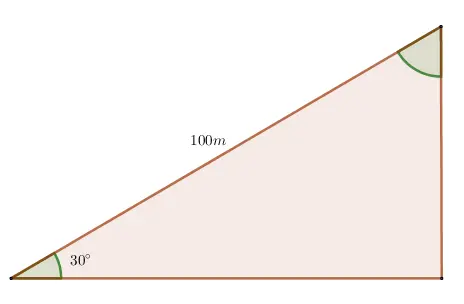
2. Hallar los valores de los catetos.
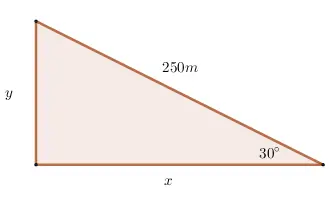
3. Calcular los lados faltantes.
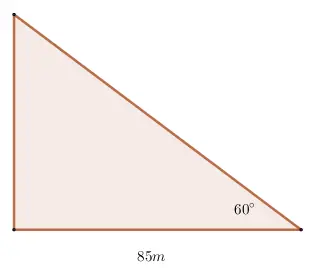
4. Determinar el perímetro.
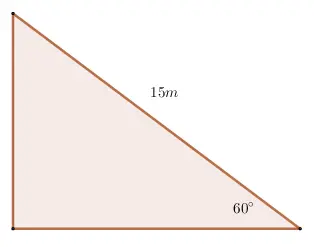
5. Calcule el área.
Respuestas:
| 1 | $$co=50\,m$$ |
| 2 | $$x = 125\sqrt{3}\,m$$ |
| $$y = 125\,m$$ | |
| 3 | $$h=170\,m \quad \text{y} \quad co=85\sqrt{3}\,m$$ |
| 4 | $$P=\frac{15(3+\sqrt{3})}{2}\,m$$ |
| 5 | $$A=2700(2\sqrt{3}+3)\,m^{2}$$ |
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión

Encontre un error en el ejercicio 3, da 170m la hipotenusa, mientrás que aquí dicen que es 85m. También encontre un error en el ejercicio 5, me dio 2700m2 (2 Raiz de 3 + 3), mientrás que aquí dice otro resultado.
Me parecico muy buena la dinámica que se uso, ya que al mostrar la respuestas de los ejercicios, ayuda mucho a conseguir un error en nuestro procedimiento y analizarlo más
Muchas gracias por tomarte el tiempo de revisar los ejercicios y compartir tu observación. Efectivamente, después de verificar nuevamente los procedimientos, confirmo que los resultados de los ejercicios 3 y 5 presentaban un error. Ya han sido corregidos para garantizar la precisión del contenido.
Comentarios como el tuyo son muy valiosos, ya que contribuyen a mejorar la calidad del material y también reflejan un excelente nivel de análisis y compromiso con el aprendizaje.
Me alegra saber que la dinámica de mostrar las respuestas te resulta útil, pues el objetivo es precisamente fomentar la verificación, la reflexión y el desarrollo del pensamiento matemático.
¡Gracias nuevamente por tu aporte y por ser parte activa de este proceso de aprendizaje!