Si estás buscando rectas y puntos notables de un triángulo, no te vayas, este es el lugar correcto para profundizar en este tema. Para ello, comenzaremos con este ejemplo de la vida diaria: Pedro es un hacendado que tiene una casa y una granja donde cría ganado, vacas, caballos, ovejas y cerdos, actualmente la población es cada vez más elevada y requiere de tres veterinario y dos ayudantes.
Para esta situación, piensa crear dos casas, una para los médicos y otra para los ayudantes. Pero desea que todas las casas estén a la misma distancia respecto a la granja, para que todos lleguen al mismo tiempo y atiendan a sus animales. Para esto contrata un ingeniero y este soluciona esta situación aplicando el circuncentro, este circuncentro es donde ubica a la granja para que las tres casas lleguen a tener las mismas distancias.
¿Qué son la rectas notables de un triángulo?
Son rectas concurrentes que expresan varias particularidades específicas, como sus puntos de concurrencia o puntos notables, propiedades geométricas, relaciones con la circunferencia y el tipo de triángulo.
¿Cuántos tipos de rectas notables existen en un triángulo?
Existen cuatro tipos de rectas nobles, cada una con características y funciones geométricas específicas, ellas son llamadas:
- Medianas,
- Bisectrices,
- Alturas y
- Mediatrices.
Truco de memoria # 1
Para facilitar tu aprendizaje y la memorización, a lo largo de este post se identificará a este conjunto de rectas con las siglas MBAM, formada por la inicial de cada una:
M → Medianas.
B → Bisectrices.
A → Alturas.
M → Mediatrices.
Recuerda la palabra MBAM como una clave rápida para no olvidar ninguna de las rectas notables del triángulo.
¿Qué son los puntos notables de un triángulo?
En un triángulo existen cuatro puntos notables, los cuales se obtienen a partir de la intersección de las rectas notables. Estos puntos concentran propiedades interesantes lo cual ayuda analizar el equilibrio, la simetría y el comportamiento geométrico del triángulo.
¿Qué nombre reciben estos puntos?
Son denominados con el nombre de:
- Baricentro.
- Incentro.
- Ortocentro.
- Circuncentro.
Truco de memoria # 2
Para facilitar tu aprendizaje y la memorización, el conjunto de estos puntos se identificará con las siglas MBAM, formada por la inicial de cada uno:
B → Baricentro.
I → Incentro.
O → Ortocentro
C → Circuncentro.
¿Cómo se obtiene el baricentro y para qué sirve?
Se obtiene al trazar las tres medianas del triángulo, las cuales se intersecan en un punto común denominado baricentro y sirve para:
- Representar el equilibrio o centro de gravedad del triángulo
- Divide cada mediana en una razón 2:1.
¿Cómo se forma el incentro y qué finalidad tiene?
Se forma cuando se intersecan las tres bisectrices. Su finalidad es:
- Representa el centro de la circunferencia inscrita, este punto siempre esta posicionado dentro de cualquier triángulo.
¿Cómo se construye el ortocentro y qué función cumple?
Se construye cuando se intersecan las tres alturas del triángulo. Su función es:
- Estudiar triángulos acutángulos, rectángulos y obtusángulos.
¿Cómo se origina el circuncentro y cuál es su utilidad?
Cuando se trazan las tres mediatrices se forma un punto llamado circuncentro. Su utilidad es la siguiente:
- Ser el centro de la circunferencia circunscrita. Este punto puede estar dentro, sobre o fuera del triángulo.
Truco de memoria # 3
Para memorizar las rectas y sus puntos notables originados se recomienda este pequeño bloque:
M → B
B → I
A → O
M → C
Explicación sencilla de las rectas notables
A continuación, te presento una explicación sencilla de cada recta y sus propiedades
Medianas de un triángulo
Lo primero que debes saber, es que son tres segmentos trazados desde los puntos medios de cada lado del triángulo hasta sus vértices opuestos.
Al dibujar las tres medianas en el triángulo estas líneas llegan a concurrir en un punto llamado baricentro.
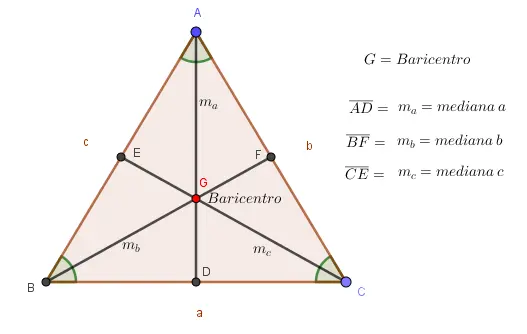
Propiedades de las medianas
Las medianas de un triángulo presentan varias propiedades geométricas importantes que es fundamental conocer y comprender, ya que permiten analizar la estructura del triángulo y resolver diversos problemas geométricos. A continuación, las principales propiedades de las medianas:
I. Cada mediana dibujada divide al triángulo en dos áreas iguales. Observa la imagen:
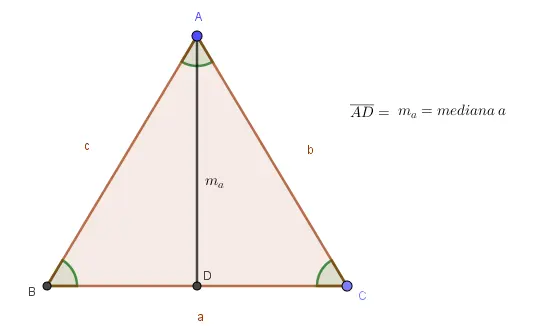
II. El punto donde concurren las tres medianas es llamado baricentro representando el centro de masa del triángulo.
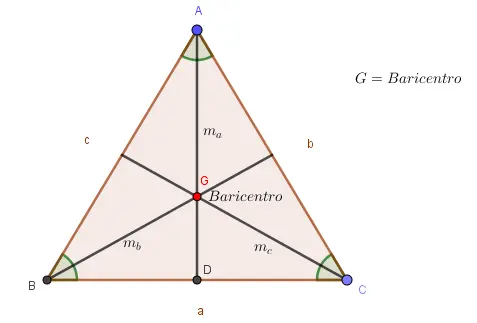
III. Para todo tipo de triángulo el baricentro es localizado en el interior del triángulo.
IV. El baricentro divide en dos segmentos a la mediana, donde uno de ellos es el doble que el otro. La parte del segmento dirigida del vértice del triángulo al baricentro siempre es el doble que la otra que va del baricentro a la mitad del lado opuesto del vértice.
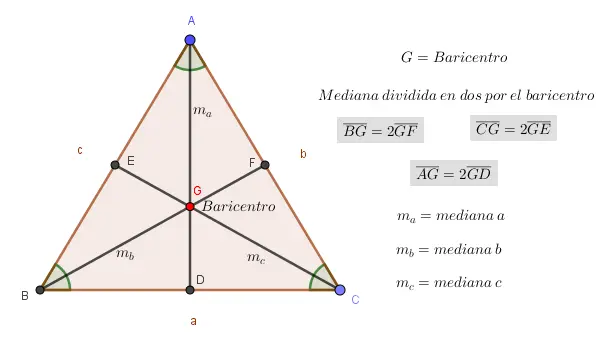
V. Si el triángulo posee el valor de todos los lados, se puede determinar la longitud de cada mediana aplicando las siguientes fórmulas:
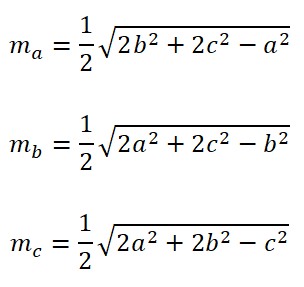
Donde:
- Longitud de la mediana correspondiente al lado a: ma
- Esta longitud de la mediana corresponde al lado b: mb
- Longitud de la mediana correspondiente al lado c: mc
Mediatrices de un triángulo
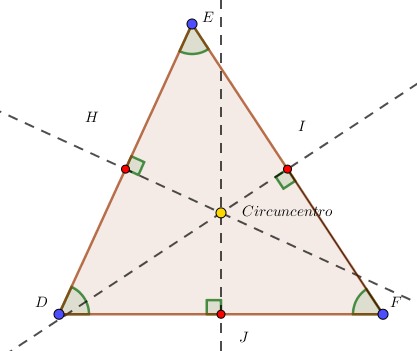Son rectas perpendiculares trazadas desde el punto medio de cada lado del triángulo. Estas tres mediatrices concurren en un punto llamado circuncentro.
Propiedades de las mediatrices
Las propiedades de las mediatrices son:
I. En primer lugar, el punto circuncentro representa el centro de una circunferencia circunscrita que pasa por los vértices del triángulo.
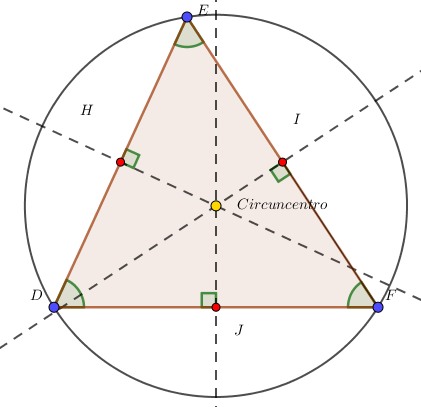
II. Posteriormente, el circuncentro equidista de los tres vértices del triángulo, es decir es la misma distancia del circuncentro a cualquier vértice del triángulo.
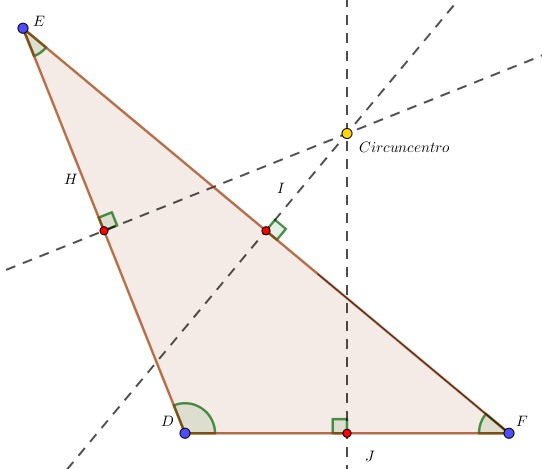
III. Por último, hay que tener en cuenta que las ubicaciones del circuncentro varía dependiendo del tipo de triángulo:
Lo primero, es que para el acutángulo, el circuncentro se ubica en la zona interna del triángulo.
Por consiguiente, para el rectángulo, la ubicación del circuncentro es en la mitad de la hipotenusa.
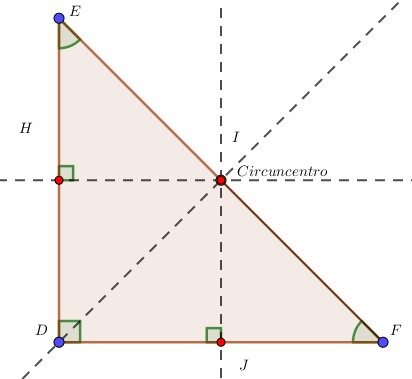
Asimismo, en el obtusángulo, el circuncentro es posicionado en el exterior del triángulo.
Alturas de un triángulo
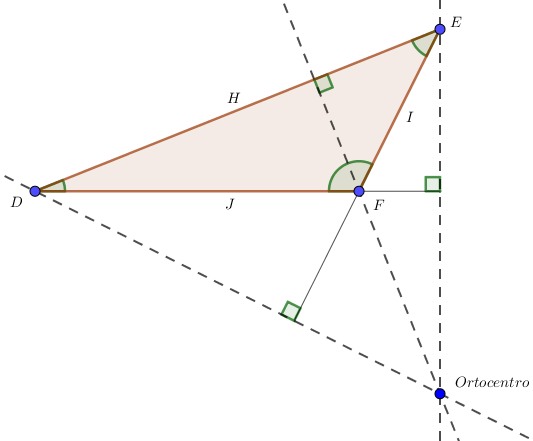Son segmentos trazados perpendicularmente respecto a cada lado del triángulo hasta su vértice opuesto.
Como resultado, estas 3 alturas del triángulo concurren en un punto llamado ortocentro.
Propiedades de las alturas
Asimismo, aquí tienes las propiedades de las alturas son:
I. En primer lugar, se encuentra el ortocentro, el cual es ubicado dependiendo el tipo de triángulo:
Lo primero, es saber que en el acutángulo, el ortocentro es ubicado en el interior del triángulo.
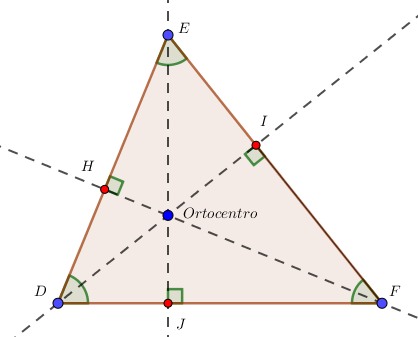
Asimismo, en el rectángulo, el ortocentro se encuentra en el vértice del ángulo recto.
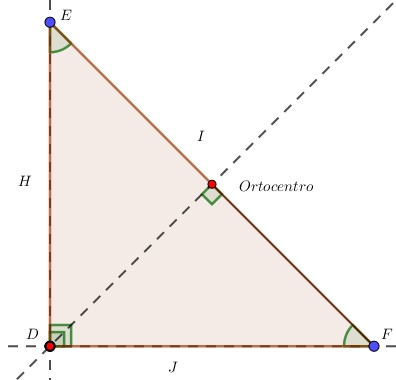
Por último, en el obtusángulo, el circuncentro está en el exterior del triángulo.
II. Posteriormente, hay que tener en cuenta las alturas son esenciales para el cálculo del área de un triángulo.
Bisectrices de un triángulo
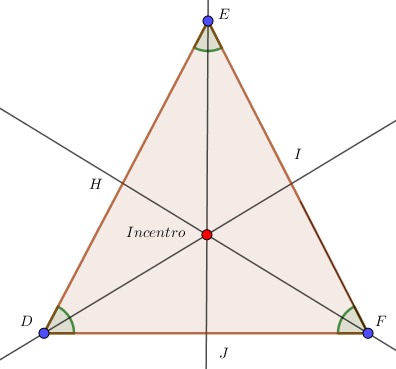Mientras tanto, las bisectrices son rectas que dividen al ángulo en dos partes iguales, al formarse las tres rectas concurren en un punto llamado incentro.
Propiedades de las bisectrices
Son varias las propiedades de las bisectrices ellas son:
I. En primer lugar, se encuentra el incentro siempre es ubicado en el interior de cualquier triángulo.
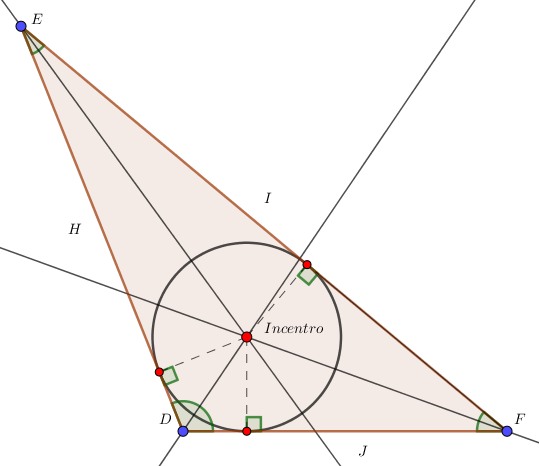
II. Además, la segunda propiedad es el punto incentro, es el centro de una circunferencia inscrita en el triángulo. Claro está, esta circunferencia siempre toca cada lado del triángulo, es decir que es tangente a cada uno de ellos.
III. Finalmente, la distancia es igual desde el incentro hasta cada lado del triángulo midiéndose de forma perpendicular.
Cuestionario
¿Te animas a comprobar qué tanto dominas las rectas y los puntos notables del triángulo? 📐
Te invito a que presentes un cuestionario corto y dinámico te ayudará a reforzar lo aprendido, aclarar dudas y ganar seguridad en geometría. No es solo para evaluar, sino para aprender mientras practicas. Haz clic, respóndelo con calma y descubre tu nivel. ¡Tú puedes!
Tabla resumen
Aquí te muestro una tabla para que memorices fácilmente cada recta y su punto notable con una característica resaltante.
Rectas | Sigla | Puntos | Sigla | Combinación de la iniciales | Características resaltantes |
Medianas | MBAM | Baricentro | BIOC | M → B | Se logra el centro de gravedad en el triángulo. |
Bisectrices | Incentro | B → I | Representa el centro de una circunferencia inscrita en el triángulo. | ||
Alturas | Ortocentro | A → O | Las alturas son fundamentales en el cálculo de áreas. | ||
Mediatrices | Circuncentro | M → C | Representa el centro de una circunferencia circunscrita en el triángulo. |
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
Por último, aquí te dejo algunas actividades para que refuerces el contenido aprendido. Por lo tanto, no esperes más y pon manos a la obra.
I. Construye un triángulo isósceles y encuentra el circuncentro, baricentro, y el incentro ¿Dónde quedan ubicados los puntos?
II. Dibuja un triángulo equilátero y encuentra todos los puntos notables. ¿Qué pasa con los puntos?
III. La distancia del baricentro de un triángulo al punto medio de un lado es de 7cm. ¿Cuánto mide la mediana?
IV. La distancia del baricentro a un vértice es 10cm. ¿Cuál es el valor de la mediana?
V. Una de las medianas de un triángulo mide 20cm. ¿Cuál es la distancia del vértice al baricentro?
Finalmente, ahora que ya conoces más acerca de las rectas y puntos notables de un triángulo es momento que profundices en el tema con la práctica. También comenta y comparte este contenido, de esta manera nos ayudas a crecer.