28 ecuaciones trigonométricas resueltas paso a paso

¿Quieres ver y aprender el procedimiento de 28 ecuaciones trigonométricas resueltas paso a paso?
En esta guía encontrarás cada ejercicio desarrollado con claridad: despejes ordenados, aplicación de identidades trigonométricas y comprobaciones finales para que no solo obtengas la respuesta, sino que entiendas por qué funciona. Ideal para reforzar clases, preparar exámenes o practicar con confianza. Sigue los pasos y transforma la resolución de ecuaciones trigonométricas en algo lógico y manejable.

Ecuaciones trigonométricas

Las ecuaciones trigonométricas son igualdades que poseen una o varias funciones trigonométricas donde la incógnita es el ángulo del cual depende la función.

¿Cómo resolver una ecuación trigonométrica?

Para resolver una ecuación trigonométrica debes transformar las funciones a una sola expresión, utilizando identidades trigonométricas. Una vez que la ecuación está en términos de una sola función, se aplican técnicas algebraicas para despejarla y, finalmente, resuelves la parte trigonométrica para encontrar el ángulo.

Aquí te presento los pasos generales a seguir:

1.Simplificar la ecuación:

1. Utilizar identidades trigonométricas para reescribir la ecuación de manera que contenga la menor cantidad de funciones trigonométricas diferentes posible, idealmente una sola.
2. Aplicar diferencia de cuadrados o factorización.
3. Si es necesario, sustituir la expresión trigonométrica con una variable simple (como x o u) para que la ecuación se asemeje a una ecuación algebraica (por ejemplo, una cuadrática).

2.Despejar la función trigonométrica para encontrar el valor del ángulo.

3.Como las funciones trigonométricas son periódicas, siempre habrá múltiples soluciones. Para determinar las soluciones es importante tener en cuenta el círculo unitario y los signos de las funciones en cada cuadrante para hallar todas las soluciones en el intervalo deseado (frecuentemente [0,2]).

Identidades de cofuncionalidad

Para resolver las ecuaciones trigonométricas también es aplicable las identidades de cofuncionalidad, ellas son:

$$\text{En grados sexagesimales:}$$

$$sin(90^\circ-x)=cosx$$

$$cos(90^\circ-x)=senx$$

$$tan(90^\circ-x)=cotx$$

$$cot(90^\circ-x)=tanx$$

$$sec(90^\circ-x)=cscx$$

$$csc(90^\circ-x)=secx$$

$$\text{O en radianes:}$$

$$sin\left(\frac{\pi}{2} – x\right)= cos x$$

$$cos\left(\frac{\pi}{2} – x\right)= sen x$$

$$tan\left(\frac{\pi}{2} – x\right)= cot x$$

$$cot\left(\frac{\pi}{2} – x\right)= tan x$$

$$sec\left(\frac{\pi}{2} – x\right)= csc x$$

$$csc\left(\frac{\pi}{2} – x\right)= sec x$$

Identidad trigonométrica de combinación lineal

Es la combinación lineal de senos y cosenos en una única función trigonométrica. Es una herramienta clave para la solución de ecuaciones trigonométricas.

Su forma es la siguiente:

$$a\cdot cosx+b\cdot senx$$

Al estar así puede ser transformado en una única función de seno o coseno.

La combinación lineal de seno y coseno se puede escribir así:

$$a\cdot cosx+b\cdot senx=R\cdot cos(x-\alpha )$$

$$a\cdot cosx+b\cdot senx=R\cdot sen(x+\beta )$$

Donde R representa la amplitud del coseno o seno, R es la longitud del vector resultante de las componentes a y b en el plano cartesiano.

Fórmulas

R: Magnitud de la combinación o amplitud resultante.

$$R=\sqrt{a^{2}+b^{2}}$$

α y β = Ángulo de fase.

Para el coseno

$$tan\alpha =\frac{b}{a}$$

Se aplica:

$$a\cdot cosx+b\cdot senx=R\cdot cos(x-\alpha )$$

Para el seno

$$tan\beta =\frac{a}{b}$$

Se aplica:

$$a\cdot cosx+b\cdot senx=R\cdot sen(x+\beta )$$

Relación entre ángulos:

$$R\cdot cos(x-\alpha )=R\cdot sen(x+\beta )$$

$$\beta =90^{\circ }-\alpha $$

Guía de 28 ecuaciones trigonométricas resueltas paso a paso para fortalecer tus habilidades

A continuación, te presento 28 ecuaciones trigonométricas resueltas paso a paso. Te recomiendo que intentes resolver cada una por tu cuenta antes de mirar la solución. ¡Así es como realmente se aprende y se consolida el conocimiento! Con práctica y dedicación, te sorprenderá lo rápido que te conviertes en un experto en la resolución de estas ecuaciones esenciales.

Ejercicio 1:

$$\tan x – \sqrt{3} = 0$$
$$\tan x – \sqrt{3} = 0$$
$$\tan x = \sqrt{3}$$
$$x=tang^{-1}\sqrt{3}=60^{\circ }$$

Análisis: Como la tangente es positiva, la solución se encuentra en el cuadrante I y III.

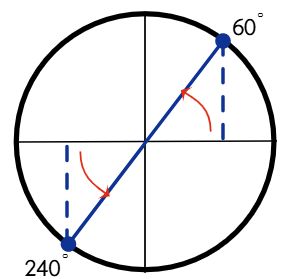
Solución:

$$x = 60^\circ, 240^\circ$$

Ejercicio 2:

$$\tan x + \sqrt{3} = 0$$
$$\tan x = -\sqrt{3}$$
$$x = \tan^{-1}(-\sqrt{3}) = 120^\circ$$

Análisis: La tangente es negativa, por lo tanto la solución está en los cuadrantes II y IV

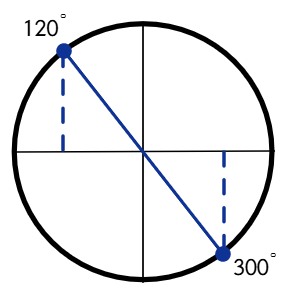
Solución:

$$x = 120^\circ, 300^\circ$$

Ejercicio 3:

$$\cot x – 1 = 0$$
$$\cot x = 1$$
$$x = \cot^{-1} 1 = 45^\circ$$

Análisis: La cotangente es positiva y su solución está en los cuadrantes I y III.

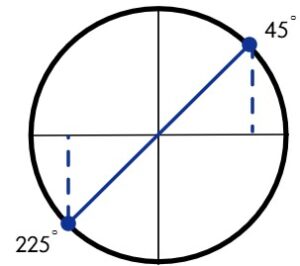
Solución:

$$x = 45^\circ, 225^\circ$$

Ejercicio 4:

$$\cot x + 1 = 0$$
$$\cot x = -1$$
$$x = \cot^{-1}(-1) = 135^\circ$$

Análisis: La cotangente es negativa y su solución está en los cuadrantes II y IV

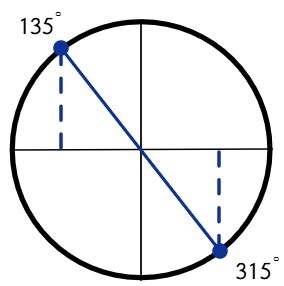
Solución:

$$x = 135^\circ, 315^\circ$$

Ejercicio 5:

$$\sec x – 2 = 0$$
$$\sec x = 2$$
$$x = \sec^{-1} 2 = 60^\circ$$

Análisis: La secante es positiva, su solución es el cuadrante I y IV.

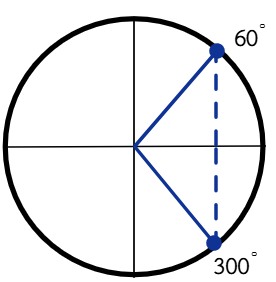
Solución:

$$x = 60^\circ, 300^\circ$$

Ejercicio 6:

$$\sec x + 2 = 0$$
$$\sec x = -2$$
$$\frac{1}{cosx}=-2$$
$$1=-2cosx$$
$$cosx=-\frac{1}{2}$$
$$x=cos^{-1}-\frac{1}{2}$$
$$x=120^{\circ }$$

Análisis: La secante es negativa, entonces su solución está en el cuadrante II y III.

Solución:

$$x = 120^\circ, 240^\circ$$

Ejercicio 7:

$$2sen x + \sqrt{1} = 0$$
$$2sen x + 1 = 0$$
$$sen x = -\frac{1}{2}$$

Solución:

$$x = 210^\circ, 330^\circ$$

Ejercicio 8:

$$2\cos x – \sqrt{12} = 0$$
$$\cos x = \frac{\sqrt{12}}{2} = \sqrt{3}$$

Solución:

$$\text{Sin solución (}\cos x = \sqrt{3} > 1\text{)}$$

Ejercicio 9:

$$8sen x + \sqrt{48} = 0$$
$$sen x = -\frac{\sqrt{48}}{8} = -\frac{4\sqrt{3}}{8} = -\frac{\sqrt{3}}{2}$$

Solución:

$$x = 240^\circ, 300^\circ$$

Ejercicio 10:

$$2\sec x – 6 = 0$$
$$\sec x = 3$$
$$\cos x = \frac{1}{3}$$

Solución:

$$x \approx 70.53^\circ, 289.47^\circ$$

Ejercicio 11:

$$2\cot x = 3$$
$$\cot x = \frac{3}{2}$$
$$x \approx 33.69^\circ, 213.69^\circ$$

Solución:

$$x \approx 33.69^\circ, 213.69^\circ$$

Ejercicio 12:

$$\sec x = \sqrt{2}$$
$$\cos x = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$$

Solución:

$$x = 45^\circ, 315^\circ$$

Ejercicio 13:

$$\sqrt{3}\cot x = -1$$
$$\cot x = -\frac{1}{\sqrt{3}} = -\frac{\sqrt{3}}{3}$$
$$\tan x = -\sqrt{3}$$

Solución:

$$x = 120^\circ, 300^\circ$$

Ejercicio 14:

$$(2sen x – \sqrt{3})(2\cos x – \sqrt{2}) = 0$$

Se iguala ambos factores a cero.

Primera ecuación:

Segunda ecuación:

Solución:

$$x = 45^\circ, 60^\circ, 120^\circ, 315^\circ$$

Ejercicio 15:

$$2sen x – cos x = -sen x$$
$$3sen x = cos x$$
$$tan x = \frac{1}{3}$$

Solución:

$$x \approx 18.43^\circ, 198.43^\circ$$

Ejercicio 16:

$$(\tan x – \sqrt{3})(\tan^2 x – 1) = 0$$

Se igualan ambos factores a cero, quedando de la siguiente manera:

Primera ecuación:

$$\tan x = \sqrt{3} \Rightarrow x = 60^\circ, 240^\circ$$

Segunda ecuación:

Solución:

$$x = 45^\circ, 60^\circ, 135^\circ, 225^\circ, 240^\circ, 315^\circ$$

Ejercicio 17:

$$2sen^2 x + sen x = +1$$
$$2sen^2 x + sen x – 1 = 0$$

Resolver con la fórmula general:

$$senx=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$$

Donde:

$$a=2;b=1;c=-1$$

Solución:

$$sen x = \frac{1}{2} \Rightarrow x = 30^\circ, 150^\circ$$
$$sen x = -1 \Rightarrow x = 270^\circ$$

Entonces:

$$x = 30^\circ, 150^\circ, 270^\circ$$

Ejercicio 18:

Se lleva todo a un lado de la ecuación:

$$3\tan^2 x – 2\sqrt{3}\tan x – 3 = 0$$

Fórmula general:

$$t=tanx$$

$$t= \frac{2\sqrt{3} \pm \sqrt{(-2\sqrt{3})^2 – 4(3)(-3)}}{2(3)}$$

$$t = \frac{6\sqrt{3}}{6} = \sqrt{3}, \quad t = \frac{-2\sqrt{3}}{6} = -\frac{\sqrt{3}}{3}$$

Entonces:

$$\tan x = \sqrt{3} \Rightarrow x = 60^\circ, 240^\circ$$
$$\tan x = -\frac{\sqrt{3}}{3} \Rightarrow x = 150^\circ, 330^\circ$$

Solución:

$$x = 60^\circ, 150^\circ, 240^\circ, 330^\circ$$

Ejercicio 19:

$$2\cos^2 x – 3\cos x – 2 = 0$$

$$2y^2 – 3y – 2 = 0$$

$$\text{Paso 3: Usar la fórmula general:}$$

$$y = \frac{3 \pm 5}{4}$$

$$y_2 = \frac{-2}{4} = -\frac{1}{2} \quad (\text{válida})$$

$$\text{Paso 4: Volver a } \cos x: \quad \cos x = -\frac{1}{2}$$

Solución:

$$\boxed{x = 120^\circ,\ 240^\circ}$$

Ejercicio 20:

$$\Rightarrow \sin x = \cos x$$

$$\tan x = 1$$

Solución:

$$\boxed{x = 45^\circ,\ 225^\circ}$$

Ejercicio 21:

$$3\cos^2 x + sen^2 x = 3$$

Se aplica la identidad pitagórica:
$$sen^2 x = 1 – \cos^2 x$$

Sustitución:
$$3\cos^2 x + (1 – \cos^2 x) = 3$$
$$2\cos^2 x + 1 = 3 \Rightarrow 2\cos^2 x = 2$$
$$\cos^2 x = 1 \Rightarrow \cos x = \pm1$$

Solución:

$$x = 0^\circ, 180^\circ$$

Ejercicio 22:

$$sec x (2sen x + 1) – 2(2sen x + 1) = 0$$
Factor común:

$$(2sen x + 1)(sec x – 2) = 0$$

Caso 1:

Caso 2:

Solución:

$$x = 60^\circ, 210^\circ, 300^\circ, 330^\circ$$

Ejercicio 23:

$$2cos^2 x + 3sen x = 0$$

Aplicación de la identidad pitagórica: $$cos^2 x = 1 – sen^2 x$$

$$2(1 – sen^2 x) + 3sen x = 0$$
$$2 – 2sen^2 x + 3sen x = 0$$
Se multiplica por -1:

$$2sen^2 x – 3sen x – 2 = 0$$

Resolver con la fórmula general:

Solución:

$$x = 210^\circ, 330^\circ$$

Ejercicio 24:

$$4\cos x – 2 = 2\left( \frac{\sin x}{\cos x} \cdot \frac{\cos x}{\sin x} \right) – \frac{1}{\cos x}$$

Solución:

$$x= 60^\circ \quad \text{y} \quad x = 300^\circ$$

$$\boxed{x = 60^\circ \quad \text{y} \quad x = 300^\circ}$$

Ejercicio 25:

$$(2 – \sqrt{3})sen x + (2 – \sqrt{3}) = 2cos^2 x$$
Se aplica la identidad pitagórica para que todo quede expresado en función a senx
$$(2 – \sqrt{3})sen x + (2 – \sqrt{3}) = 2(1 – sen^2 x)$$
Propiedad distributiva en el segundo miembro de la ecuación:
$$(2 – \sqrt{3})sen x + (2 – \sqrt{3}) = 2 – 2sen^2 x$$
Se iguala a cero:

Ecuación de 2° grado en senx
$$2sen^2 x + (2 – \sqrt{3})sen x – \sqrt{3} = 0$$

Sustitución en la fórmula general:

Cálculo del discriminante:

$$(2 – \sqrt{3})^2 = 4 – 4\sqrt{3} + 3 = 7 – 4\sqrt{3}$$
$$4ac = 4(2)(-\sqrt{3}) = -8\sqrt{3}$$
Discriminante total:
$$7 – 4\sqrt{3} + 8\sqrt{3} = 7 + 4\sqrt{3}$$

Entonces:

$$sen x = \frac{-(2 – \sqrt{3}) \pm \sqrt{7 + 4\sqrt{3}}}{4}$$

Valor de:
$$sen x_1 \approx 0.866 \Rightarrow x = 60^\circ, 120^\circ$$
$$sen x_2 \approx -1 \Rightarrow x = 270^\circ$$

Solución:

$$\boxed{60^\circ, 120^\circ, 270^\circ}$$

Ejercicio 26:

$$\sqrt{2} cos x – \sqrt{2} sen x = -\sqrt{3}$$

$$a cos x + b sen x = R \cos(x – \alpha)$$

$$\textbf{2.1. Calculo de } R:$$

$$\textbf{2.2. Calcular del ángulo } \alpha:$$

$$\tan \alpha = \frac{b}{a} = \frac{-\sqrt{2}}{\sqrt{2}} = -1$$

$$\textbf{Paso 3: Reescribir la ecuación}$$

$$\sqrt{2} cos x – \sqrt{2} sen x = 2 cos(x + 45^\circ)$$

$$2 \cos(x + 45^\circ) = -\sqrt{3}$$

$$\textbf{Paso 4: Despejar}$$

$$\cos(x + 45^\circ) = -\frac{\sqrt{3}}{2}$$

$$x + 45^\circ = 150^\circ \Rightarrow x = 105^\circ$$

$$x + 45^\circ = 210^\circ \Rightarrow x = 165^\circ$$

Solución

Ejercicio 27:

$$\frac{1}{\cot^2 x} + \sqrt{3} \tan x = 0$$
$$\frac{1}{\cot^2 x} = \tan^2 x$$
Entonces:

$$\tan^2 x + \sqrt{3}\tan x = 0$$
$$\tan x (\tan x + \sqrt{3}) = 0$$

$$\tan x = 0 \Rightarrow x = 0^\circ, 180^\circ$$
$$\tan x = -\sqrt{3} \Rightarrow x = 120^\circ, 300^\circ$$

Solución:

$$x = 0^\circ, 120^\circ, 180^\circ, 300^\circ$$

Ejercicio 28:

$$2cos\left( \frac{\pi}{4} – x \right) = 1$$

$$\text{Paso 1: Conversión a grados: } \frac{\pi}{4} = 45^\circ$$

$$\Rightarrow \cos(45^\circ – x) = \frac{1}{2}$$

$$\text{Paso 3: Se determina los valores de x:}$$

$$45^\circ-x=60^\circ$$

$$x=-15^\circ$$

$$45^\circ-x=300^\circ$$

$$x=-255^\circ$$

$$x=-15^\circ+360^\circ$$

$$x=345^\circ$$

$$x=-255^\circ+360^\circ$$

$$x=105^\circ$$

Solución

$$\boxed{x = 105^\circ,\ 345^\circ}$$

¿Tienes dudas o quieres compartir tu propio ejercicio?

¿Te gustaron los 28 ecuaciones trigonométricas resueltas paso a paso?

Si tienes un ejercicio de ecuaciones trigonométricas que te gustaría que resolviera, ¡escríbelo en los comentarios! También puedes dejar tus sugerencias, dudas o ideas para mejorar este contenido.

¿Aceptas el reto? Suscríbete y envía 28 ecuaciones trigonométricas resueltas paso a paso y recibirás una revisión completa: correcciones, métodos alternativos y consejos prácticos.

¡Estoy atento a tus aportes para seguir creando recursos que te ayuden a aprender mejor!

© LaProfeMatematik · Aprender con amor de Dios y mucha pasión