Circunferencia trigonométrica

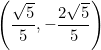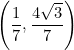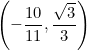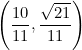
¿Has escuchado el término circunferencia trigonométrica y te has preguntado por qué la llaman así? La respuesta es simple: gracias a su forma, es posible dibujar una serie de triángulos rectángulos. A partir de esta geometría, se definen las razones trigonométricas como el seno, el coseno y la tangente. Debido al surgimiento de estas razones, a la circunferencia se le da el nombre de Circunferencia Trigonométrica.

La circunferencia trigonométrica, también conocida como círculo unitario, es una herramienta fundamental en matemáticas, con aplicaciones directas en la vida real. Desde la ingeniería y la física, para calcular la trayectoria de un péndulo o la propagación de una onda de sonido, hasta la navegación y los videojuegos, donde se utiliza para determinar posiciones y rotaciones, este simple círculo es la base para entender cómo los ángulos se relacionan con el movimiento y las fuerzas.

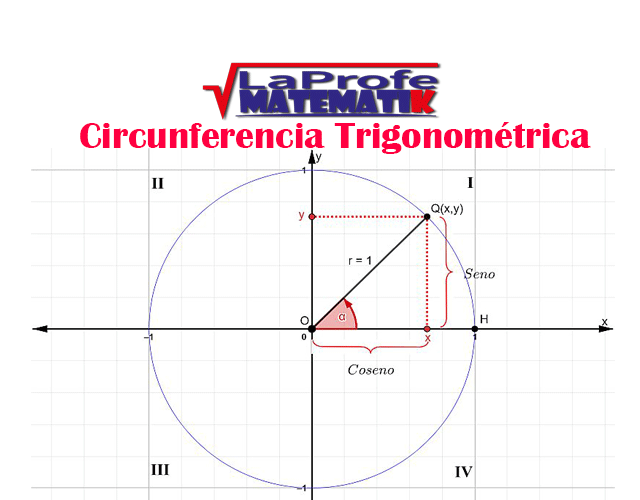
Circunferencia trigonométrica

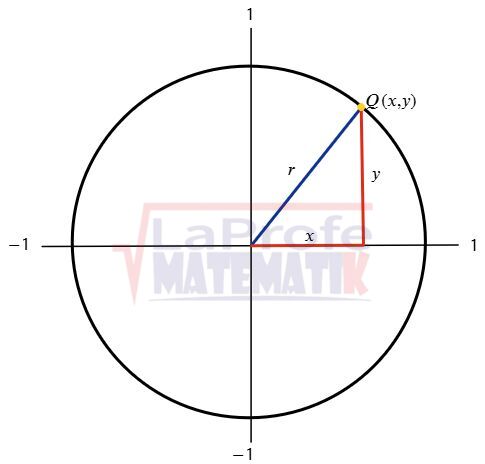
La siguiente imagen, muestra el ángulo α cuyo lado inicial es   y cuyo lado final es , ambos segmentos son radios de la circunferencia. Cuando el lado final en posición normal termina en el punto Q(x, y), estas coordenadas se proyectan sobre los ejes cartesianos, formando un triángulo rectángulo, cuya hipotenusa es el radio (o sea, 1). A medida que el lado final del ángulo gira, se forman más triángulos rectángulos.

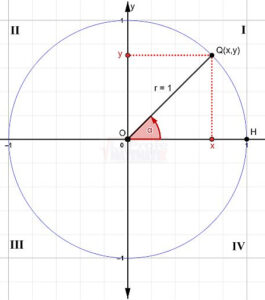
En la circunferencia trigonométrica, el teorema de Pitágoras es siempre aplicable. Dado que cualquier punto Q ( x, y ) en la circunferencia unitaria forma un triángulo rectángulo con el origen del plano cartesiano y sus coordenadas deben satisfacer la expresión:$$x^{2}+y^{2}=1$$
Sabiendo que:

“x”es la longitud del cateto adyacente  y  “y”es la longitud del cateto opuesto.

Ejemplo#1.

Determine si el punto M pertenece a la circunferencia unitaria.

$$M\left ( -\frac{3}{5},\frac{4}{5} \right )$$

Solución

Coordenadas:
$$x=-\frac{3}{5}$$
$$y=\frac{4}{5}$$

Se aplica: x² + y² = 1

$$\left ( -\frac{3}{5} \right )^{2}+\left ( \frac{4}{5} \right )^{2}=1$$
$$\frac{9}{25}+\frac{16}{25}=1$$
$$\frac{25}{25}=1$$
$$1=1$$

Esto quiere decir que el punto$$M\left ( -\frac{3}{5},\frac{4}{5} \right )$$pertenece a la circunferencia unitaria. 😀

El punto M ∈ Circunferencia unitaria.

Ejemplo#2.

Determinar si el punto N pertenecen o no a la circunferencia unitaria.
$$N\left ( 2,3 \right )$$

Coordenadas:
$$x=2$$
$$y=3$$

Se aplica Pitágoras:  x² + y² = 1
$$2^{2}+3^{2}=1$$
$$4+9=1$$
$$13\neq 1$$

Al dar como resultado 13 ≠ 1 el punto N  NO pertenece a la circunferencia unitaria. 🙁

Ángulos positivos y negativos

Desde el punto ( 1,0 ) se mide una distancia s a lo largo de la circunferencia unitaria, cada valor de s le toca un punto Q( x, y ). Por lo tanto, s establece un arco donde sus extremos son ( 1,0 ) y Q( x, y ).

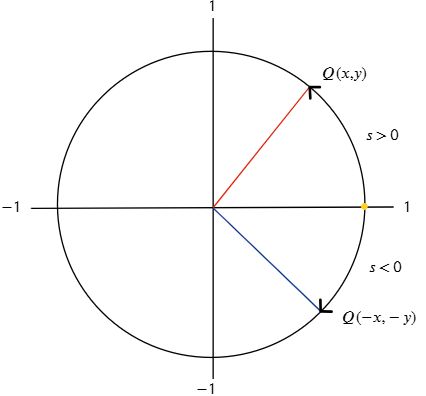
Cuando:

• s es positivo ( s > 0 ), el arco apunta en sentido contrario a las agujas del reloj.
• s resulta negativo ( s < 0 ), el arco apunta en el sentido de las agujas del reloj.

Ángulos en posición normal 

Se les denomina ángulos de posición normal ( o estándar) cuando el vértice del ángulo se dibuja con el origen ( 0,0 ) del plano cartesiano, su lado inicial es coincidente con el semi lado del eje “x” y su lado final puede girar en sentido antihorario o horario.

Esta denominación se hace para poder relacionar los ángulos con las coordenadas de un punto en la circunferencia.

Ángulos cuadrantales

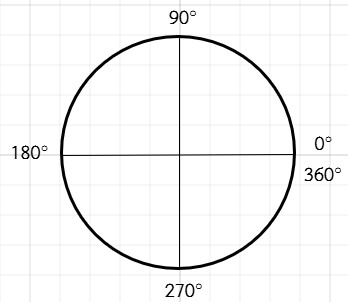
La circunferencia trigonométrica posee Ángulos cuadrantales y son aquellos ángulos en posición normal cuyo lado final coincide con uno de los semi ejes del plano. Estos ángulos son múltiplos de 90° o π/2 (radianes) y son 0°, 90°,180°, 270° y 360°.

Razones trigonométricas definidas en la circunferencia unitaria

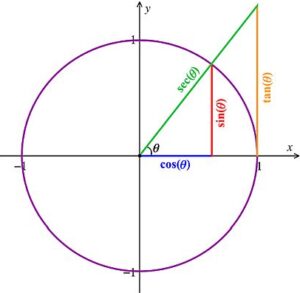
En la figura a continuación, se muestra la circunferencia unitaria. Observa que el radio tiene una longitud de 1 y que el ángulo α define el arco .

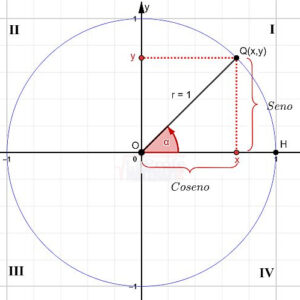
Entonces se obtienen seis razones trigonométricas

$$sen\alpha =\frac{y}{r}=\frac{y}{1}=y$$
$$cos\alpha =\frac{x}{r}=\frac{x}{1}=x$$
$$tan\alpha =\frac{y}{x}$$

$$csc\alpha =\frac{r}{y}=\frac{1}{y}$$
$$sec\alpha =\frac{r}{x}=\frac{1}{x}$$
$$ctg\alpha =\frac{x}{y}$$

De las relaciones anteriores, se deducen las siguientes relaciones:

$$csc\alpha =\frac{1}{y}=\frac{1}{sen\alpha }$$
$$sec\alpha =\frac{1}{x}=\frac{1}{cos\alpha }$$
$$tan\alpha =\frac{y}{x}=\frac{sen\alpha }{cos\alpha }$$
$$ctg\alpha =\frac{x}{y}=\frac{cos\alpha }{sen\alpha }$$

 ➡  Ejemplo

Determine las razones trigonométricas de α ∈ , si α es la medida del arco que describe los extremos (1,0) y el punto$$Q\left ( \frac{1}{2},-\frac{\sqrt{3}}{2} \right )$$

Solución

Coordenadas:

$$y=-\frac{\sqrt{3}}{2}$$
$$x=\frac{1}{2}$$

Razones trigonométricas:

$$sen\alpha =y=-\frac{\sqrt{3}}{2}$$
$$\boxed{sen\alpha =-\frac{\sqrt{3}}{2}}$$
$$cos\alpha =x=\frac{1}{2}$$
$$\boxed{cos\alpha =\frac{{1}}{2}}$$
$$tan\alpha =\frac{y}{x}=\frac{-\frac{\sqrt{3}}{2}}{\frac{1}{2}}$$
$$\boxed{tan\alpha =\sqrt{3}}$$
$$csc\alpha =\frac{1}{y}=\frac{1}{-\frac{\sqrt{3}}{2}}$$
$$=-\frac{2}{\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}}=-\frac{2\sqrt{3}}{3}$$
$$\boxed{csc\alpha =-\frac{2\sqrt{3}}{3}}$$
$$sec\alpha =\frac{1}{x}=\frac{1}{\frac{1}{2}}=2$$
$$\boxed{sec\alpha =2}$$
$$ctg\alpha =\frac{\frac{1}{2}}{-\frac{\sqrt{3}}{2}}=-\frac{1}{\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}}$$
$$\boxed{ctg\alpha =-\frac{\sqrt{3}}{3}}$$

Signo de las razones trigonométricas

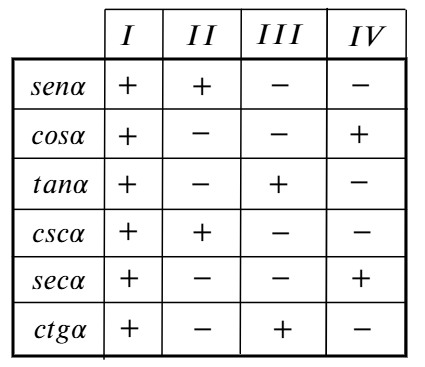
El signo de las razones trigonométricas depende de los valores x  e  y, según sus valores se ubican en cualquiera de los cuadrantes de la circunferencia unitaria, entonces los signos según la ubicación del lado final del ángulo es la siguiente:

Ángulos notables

Los ángulos notables se basan en un patrón que se repite en cada cuadrante. Por ejemplo:

I = 30°, 45°, 60°.

II = 120°, 135°, 150°.

III = 210°, 225°, 240°.

IV = 300°, 315°, 330°.

Se les llama así porque sus razones trigonométricas (como el seno, coseno, tangente, etc.) tienen valores exactos. Esto permite resolver problemas de forma rápida, sin necesidad de usar una calculadora.

Simulador de la circunferencia trigonométrica

Explora el simulador de la circunferencia trigonométrica. Desliza el punto rojo y observa cómo cambian los signos de las funciones para cada ángulo. La construcción muestra los lados de un triángulo rectángulo inscrito en la circunferencia, lo que te ayudará a comprender mejor la relación entre ángulos y razones trigonométricas.

Actividades

Determine si cada punto pertenece a la circunferencia unitaria.

A(-3,2)

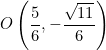
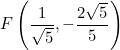
B(-5,0)

C(0,2)

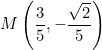
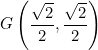
Determine el valor de la coordenada que falta, si el punto Q pertenece a la circunferencia unitaria. Al lado de cada punto indica el cuadrante.

  I cuadrante

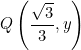IV cuadrante

III cuadrante

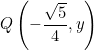II cuadrante

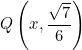I cuadrante

Determine el valor de las razones trigonométricas para α ∈ , si α es la medida del arco que describe los extremos (1,0) y el punto dado.