¿Sabes qué son las funciones trigonométricas? Considera las matemáticas como una caja de herramientas con la que puedes representar y estudiar cualquier forma o patrón.
Así como las funciones elementales (constante, afín, cuadrática, etc.) te permiten representar formas básicas como una rampa o un arco, las funciones trigonométricas son un tipo de herramienta más avanzada.
Se utilizan para modelar y describir fenómenos de la vida real que tienen un comportamiento cíclico u ondulatorio, como las ondas de sonido, el movimiento de un péndulo, o las mareas del océano.
Funciones trigonométricas
Las funciones trigonométricas son parte de las funciones trascendentes y son basadas en la circunferencia unitaria o trigonométrica.
Cuando la circunferencia trigonométrica se relaciona con las funciones trigonométricas (seno, coseno y tangente), el radio de la circunferencia actúa como la hipotenusa de un triángulo rectángulo, y las líneas trigonométricas son los catetos de ese triángulo.
Para el seno es la línea vertical que representa el cateto opuesto del triángulo, su valor corresponde a la coordenada “y” del punto en la circunferencia.
Para el coseno es la línea horizontal representante del cateto adyacente, su valor es la coordenada “x”.
La tangente se representa como una línea vertical que es tangente a la circunferencia en el punto (1,0).
La circunferencia trigonométrica es la herramienta idónea para comprender cómo se construyen las gráficas de las funciones trigonométricas.
Función seno
La función seno es de la forma$$f(x)=senx$$y es una función real de variable real. Esto se debe a que toma cada ángulo expresado en radianes (números reales) y se le asigna un único número real como resultado.
Gráfica de la función seno
El valor del seno de un ángulo corresponde a la coordenada “y” es decir la línea vertical (altura = cateto opuesto) en la circunferencia trigonométrica.
El procedimiento para graficar es siguiente:
Primero. Dibuja una circunferencia y marca cada amplitud (0, π/6, π/3, π/2, 2π/3, 5π/6, π, 7π/6, 4π/3, 3π/2, 5π/3, 11π/6, 2π) con puntos.
Segundo. Dibujar el plano cartesiano con los cuadrantes I y IV. Expresar en radianes el eje “x”.
Tercero. Cada ángulo adquiere el valor de “y” es decir una altura, esa altura es la línea trigonométrica que debe ser trasladada hasta hacerla coincidir con el ángulo trazado en el eje “x”.
Cuarto. Une los puntos para formar la curva de la función seno.
Observa:
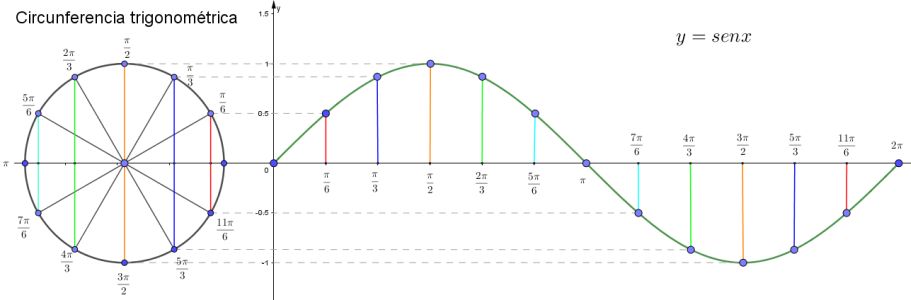
Haciéndole un acercamiento a la función:
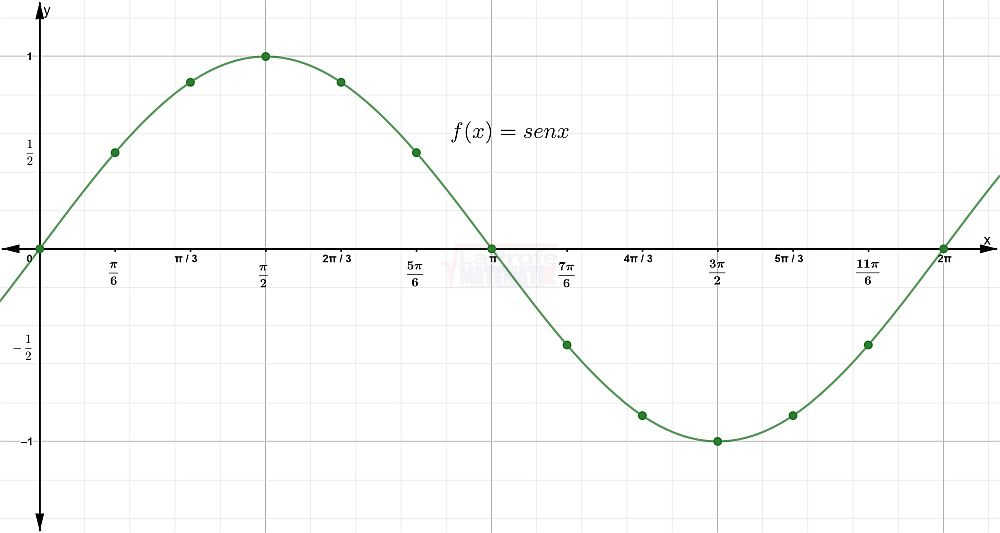
Características de la función seno
Las características de la función seno son las siguientes:
Dominio: R.
Rango: [-1, 1].
Periodo: 2π.
Continuidad: Continua ∀ x ∈ R (para todo “x” que pertenece a los reales).
Creciente: …∪ (-π/2, π/2), ∪ (3π/2, 5π/2) ∪ …
Decreciente: …∪ (π/2, 3π/2), ∪ (5π/2, 7π/2) ∪ …
Máximos: (π/2 + 2π.k, 1 ) k ∈ Z.
Mínimos: (3π/2 + 2π.k, -1 ) k ∈ Z.
Impar: sen(-x) = -sen x.
Intersección con el eje x : x = { 0 + π.k}.
Intersección con el eje y : ( 0, 0 )
Función coseno
El valor del coseno de un ángulo corresponde a la coordenada “x” es decir la línea horizontal (cateto adyacente) en la circunferencia trigonométrica. Esa línea horizontal es la línea trigonométrica para obtener la gráfica de la función seno.
Gráfica de la función coseno
Para construir la curva de la función coseno se debe:
Primero. Seguir el mismo proceso que con el seno, pero en esta ocasión debes considerar la línea trigonométrica horizontal de cada punto.
Segundo. Dibujar en el plano cartesiano cada línea trigonométrica de la circunferencia trigonométrica con la misma longitud y verticalmente.
Tercero. Unir todos los puntos para formar la función del coseno.
Observa la gráfica:
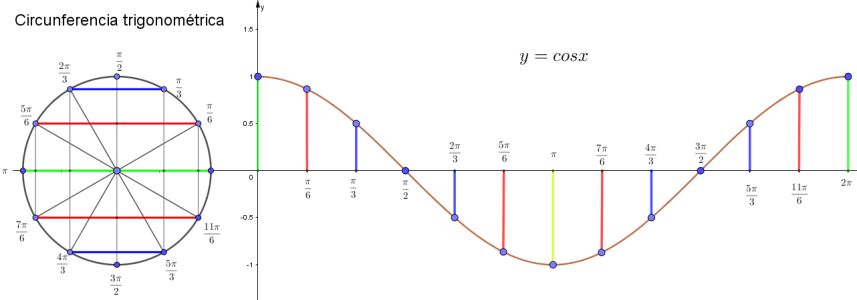
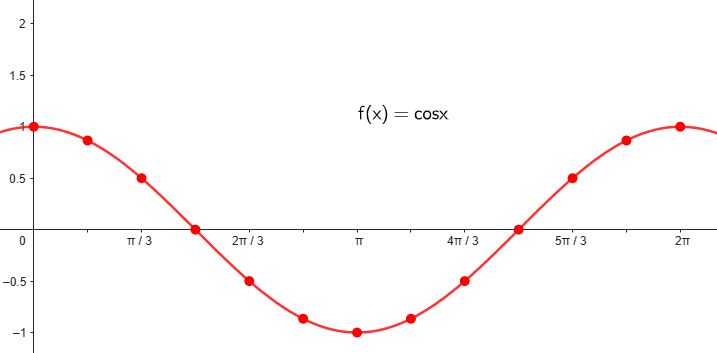
Función coseno
Características de la función coseno
La función coseno es muy utilizada para modelar fenómenos cíclicos ya que es una función periódica, como ondas de sonido, movimiento de péndulo y oscilaciones. A continuación sus características:
Dominio: R.
Rango: [-1, 1].
Periodo: 2π.
Continuidad: Continua ∀ x ∈ R (para todo “x” que pertenece a los reales).
Creciente: …∪ (-π, 0), ∪ (π, 2π) ∪ …
Decreciente: …∪ (0, π), ∪ (2π, 3π) ∪ …
Máximos: (2π.k, 1 ) k ∈ Z.
Mínimos: (k.(2k + 1 ), -1 k ∈ Z.
Par: cos(-x) = cos x.
Intersección con el eje x : x = { π/2 + k}.
Intersección con el eje y : ( 0, 1 )
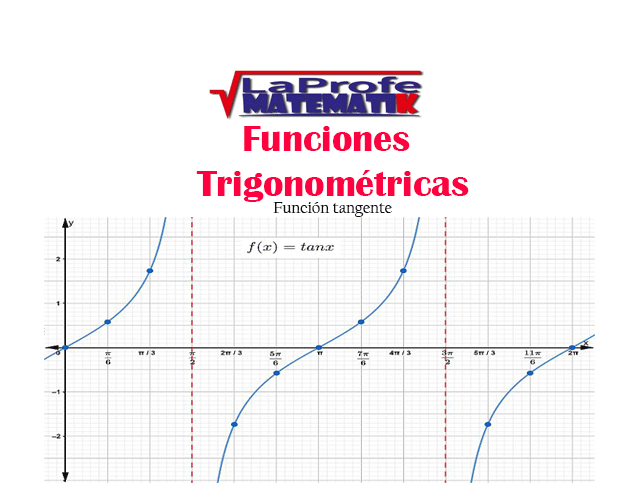
Función tangente
La función tangente es una función real de variable real, definida como$$f(x)=\frac{senx}{cosx}$$donde$$cosx\neq 0$$, es decir la función tangente es de la forma$$f(x)=tanx$$de tal forma que cada ángulo expresado en radianes se le hace corresponder un número real denotado como$$tanx$$
Gráfica de la función tangente
La tangente es la razón entre el seno y el coseno ( y / x ). Su valor se representa con una línea vertical que es la tangente de la circunferencia en el punto (1,0).
Para desarrollarla debes:
Uno: Trazar rectas tangentes a la circunferencia en posición vertical (perpendiculares respecto al eje horizontal).
Dos: Dibujar cada línea final del ángulo (desde el origen del plano cartesiano) hasta la recta tangente (línea vertical) y trazar un punto.
Tres: Identificar con un color cada línea vertical.
Cuatro: Trasladar paralelamente cada línea vertical.
Cinco: Unir los puntos para obtener la función tangente.
Gráfica de la tangente:
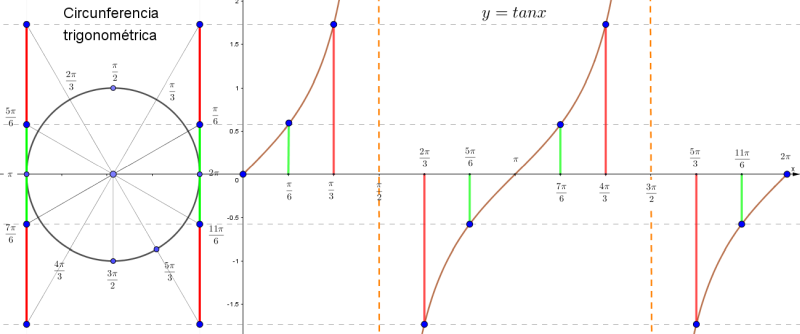
Acercamiento de la función tangente:
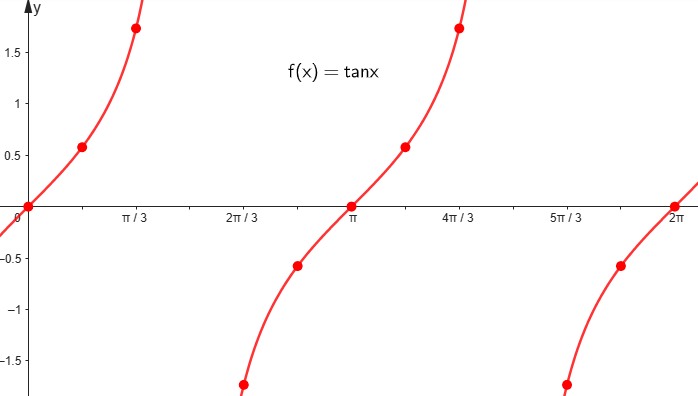
Características de la función tangente
Las características de la función tangente son las siguientes:
Dominio: R-{(2k + 1). π/2, k ∈ Z} = R-{ …, -π/2, π/2, 3π/2, … }.
Rango: R.
Periodo: π rad.
Continuidad: Continua ∀ x ∈ R – { (π/2 + π.k) }.
Creciente: R – { …, -9π/2, -π/2, π/2, 9π/2,…}.
Decreciente: …∪ (0, π), ∪ (2π, 3π) ∪ …
Máximos: No posee.
Mínimos: No posee.
Impar: tan(-x) = -tan x.
Intersección con el eje x : x = { 0 + πk} k ∈ Z.
Intersección con el eje y : ( 0, 0 ).
Simulador de las funciones trigonométricas
¡Bienvenido! Ha llegado el momento de poner en práctica todo lo aprendido. En este simulador descubrirás diversas características de las funciones trigonométricas que te permitirán fortalecer y profundizar tus conocimientos. Lo mejor de todo es que aprenderás mientras juegas.
Actividades
I.Representa gráficamente la función y = sen x en el intervalo [-π, π]. Construye la tabla de valores
II.Representa gráficamente las siguientes funciones:
$$f(x)=sen3x$$
$$f(x)=-senx$$
$$f(x)=sen4x$$
$$f(x)=sen(x-2)$$
III.Graficar la función y = cos x en el intervalo [-2π, 2π]. Construye la tabla de valores
IV.Representar gráficamente las siguientes funciones:
$$f(x)=cos(x)+1$$
$$f(x)=cos\left ( x-\frac{\pi }{4} \right )$$
$$f(x)=cos(x-2)$$
$$f(x)=cos\left ( x+\frac{\pi }{3} \right )$$
V.Representar gráficamente las siguientes funciones:
$$f(x)=-cosx$$
$$f(x)=cos6x$$
$$f(x)=cos2x$$
VI.Mencionar 3 intervalos decreciente de la función coseno.
VII.Mencionar 2 intervalos crecientes de la función tangente.
Descubre más desde LaProfematematiK "Dios es Bueno"
Suscríbete y recibe las últimas entradas en tu correo electrónico.