¿Quieres profundizar más acerca de regla de tres simple inversa? ¿Sabías qué… hasta en tus juegos favoritos o cuando pides pizza se esconde la matemática? Así es, la regla de tres simple inversa no es solo cosa de exámenes; también aparece en tu vida diaria, como cuando calculas cuánto tiempo tardas en terminar un videojuego con más amigos, o cuánto menos tarda el domiciliario o repartidor si hay menos pedidos. Si quieres mejorar en la solución de problemas, te invito a leer este tema.
¿Qué es una regla de tres simple inversa?
Es un método utilizado en situaciones donde las magnitudes que intervienen son inversamente proporcionales.
¿Cómo resolver un problema?
Para solucionarlo debes llevar a cabo los siguientes pasos:
- Análisis.
- Organización los datos por cada magnitudes.
- Crear las razones.
- Plantear una proporción invirtiendo las razones.
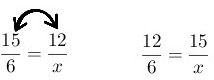
- Solucionar.
Problemas resueltos
Ahora verás, problemas resueltos paso a paso para que sepas cómo aplicar la regla de tres simple inversa en situaciones reales.
a. Una empresa de producción poseen brazos robóticos para efectuar tareas de pintado, estos brazos cuentan con un sistema de ruedas dentadas llamados tren de engranajes.
El engranaje (#1) es el que recibe el movimiento del motor llamado rueda motora, este posee 32 dientes, el engranaje (#2) 60 dientes y el engranaje (#3) 80 dientes. Si la rueda motora gira 16 vueltas ¿Cuántas vueltas dan las ruedas #2 y #3?.
Primero: Análisis.
Cuánto más dientes menor son las vueltas.
Segundo: Organización (Ruedas).
Uno = 32 dientes, da 16 vueltas.
Dos = 60 dientes, se desconoce sus vueltas.
Tres = 80 dientes, se desconoce sus vueltas.
Tercero: Razones.
| Engranaje # 1 | Engranaje # 2 | Engranaje # 3 |
 |  |  |
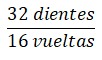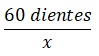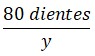Cuarto: Proporciones inversas
| Proporciones directas | Proporciones inversas | ||
 |  |  |  |
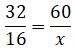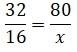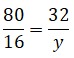Quinto: Solución.
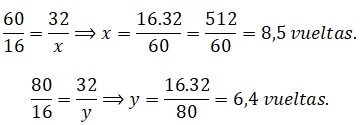
b. Un granjero tiene una cantidad de alimento suficiente para alimentar a sus pollos durante cierto tiempo. Un día vendió 90 pollos, y con eso logró que la comida durara 27 días. Si no hubiera vendido los pollos, la comida solo habría alcanzado para 18 días. ¿Cuántos pollos tenía originalmente?
Análisis. Si tiene pocos pollos la comida dura mucho más. Es decir a menor cantidad de pollos, mayor son las cantidades de días de duración de la comida.
Organización.
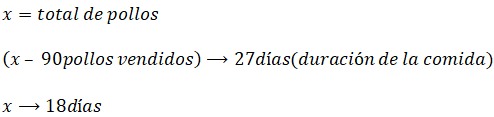
Razones.
Proporción inversa.
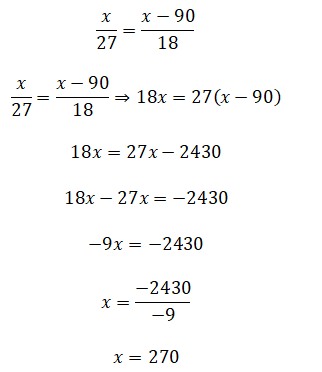
Conclusión: Inicialmente contaba con 270 pollos.
Desafío Inverso: ¡El Juego de la Proporcionalidad!
¡Bienvenidos a nuestra nueva simulación interactiva! A menudo, ya tu sabes que si una cantidad aumenta, otra también lo hará. Pero, ¿qué sucede cuando la relación es justo lo contrario? Es decir, si una cantidad crece, la otra disminuye en la misma proporción. Eso es precisamente la proporcionalidad inversa y la puedes encontrar en situaciones tan variadas como la planificación de un viaje, distribuir tareas, etc.
En esta simulación, encontrarás diferentes escenarios donde la proporcionalidad inversa es la protagonista. Prepárate para observar cómo un cambio en una variable impacta de forma opuesta a la otra, y cómo puedes utilizar este conocimiento para resolver problemas de la vida real.
¿Qué te ha pareció la simulación?
¡Nos encantaría saber tu opinión en los comentarios que está al final de este post!
¿Se te ocurre algún ejemplo de proporcionalidad inversa en tu día a día que quieras compartir? ¡Anímate a participar!
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
Resuelve los siguientes problemas.
- El gasoil utilizado para 8 tractores dura para 5,4 días. ¿Cuántos días alcanza la misma cantidad de combustible si solo se utilizan 4 máquinas?.
- Un señor tiene un negocio de ventas de cachorros, tienen alimento para 15 días. ¿Cuánto tiempo le alcanzará la comida si ahora tiene 3 cachorro más?. Nota: cada cachorro se alimenta con la misma cantidad de comida diaria.
- En una fábrica de salsa abastecen diariamente 1600 botellas con una capacidad de 1,25L. Si se quiere envasar la misma cantidad total de salsa en envases de 4L. ¿Cuántas botellas son necesarias?
Identifica qué situaciones pueden resolverse aplicando regla de tres simple inversa. Justifica tu respuesta.
- Se necesita suministrar 240mg por 4mL de agua de un medicamento en polvo. ¿Qué cantidad de agua se requiere para mezclarse con 1200mg del medicamento?
- Una gasolinera posee 2 bombas, una nueva y la otra vieja. La nueva abastece un tanque de un automóvil en 4 minutos con un rapidez de 15L/min. ¿Qué tiempo se toma la bomba vieja en llenar el tanque del mismo vehículo, si lo ejecuta a razón de 11 Litros por minutos.
- Una constructora necesita 8 trabajadores para construir una casa en 50 días. ¿Cuántos trabajadores se requieren para construir la misma casa en 20 días?
Comparte esto:
Descubre más desde LaProfematematiK "Dios es Bueno"
Suscríbete y recibe las últimas entradas en tu correo electrónico.