 ¿Alguna vez te has preguntado cómo un robot sabe el ángulo exacto para extender su brazo y recoger un objeto, o cómo tu GPS calcula el ángulo de giro para llevarte a tu destino?
¿Alguna vez te has preguntado cómo un robot sabe el ángulo exacto para extender su brazo y recoger un objeto, o cómo tu GPS calcula el ángulo de giro para llevarte a tu destino?
Detrás de estas acciones, hay una matemática fascinante: las funciones trigonométricas inversas. A diferencia de las funciones normales que usan un ángulo para darte un valor, estas funciones hacen lo opuesto: usan un valor para darte un ángulo. Son la clave para que un dron calcule su ángulo de aterrizaje, para que un personaje de videojuego apunte con precisión, o para que un brazo robótico se posicione. Dominar este tema te permitirá entender la ciencia que hace posible la tecnología que usamos a diario.
Funciones inversas
Una función es una regla de correspondencia que relaciona los elementos de dos conjuntos M y N. Cada elemento del conjunto M se relaciona únicamente con un elemento del conjunto N.
Se escribe de dos formas:
$$f: M\to N$$
o
$$f(x)=y$$
Donde:
“x” pertenece al conjunto M (dominio)
“y” pertenece al conjunto N (codominio)
Ahora si la función está definida como:$$g:N\to M$$
es una función inversa de: $$f: M\to N$$
Entonces f debe ser biyectiva.
| Si una función f es biyectiva $$f : M\to N$$ entonces existe una función inversa, denotada como: $$f^{-1} (f^{-1}: N \to M)$$ Esta función se caracteriza por deshacer el efecto de la función original. |
Dicho de forma más simple, si una función f asocia cada valor de entrada (x) con un único valor de salida (y), la función inversa f -1 hace lo opuesto, asociando (y) de vuelta a (x). Entonces, se cumple que:
$$f(f^{-1}(x))=x$$
y
$$f^{-1}(f(x))=x$$
¿Qué significado tiene esas funciones?
 Imagínate una máquina con un avance a la derecha y el otro a la inversa.
Imagínate una máquina con un avance a la derecha y el otro a la inversa.
f = Avance a la derecha.$$f(f^{-1}(x))=x$$
f -1 = Avance inverso.$$f^{-1}(f(x))=x$$
Cuando el operador desea avanzar la carga a la derecha desplaza la palanca a la derecha y cuando requiere a la inversa la mueve a la izquierda.
f (avance a la derecha) : es “sumar 2”
f -1 (avance a la inversa) : es “restar 2”
Avance a la derecha ( f )
$$f(f^{-1}(x))=x$$
- Selecciona un número cualquiera, para este ejemplo, x = 8.
- Aplicar función inversa ( f -1 ) : 8 – 2 = 6.
- Aplica función original ( f ): 6 + 2 = 8.
Observa que regresó a su número original ( x = 8 ).
Avance a inversa ( f -1 )
$$f^{-1}(f(x))=x$$
- x = 8.
- f : 8 + 2 = 10
- f -1 : 10 – 2 = 8
Nuevamente regresó al número original ( x = 8 ).
¿Cómo se obtiene una función inversa?
Para obtener la función inversa debes aplicar los siguientes pasos:
|
Ejemplos prácticos
Ahora que has dominado la teoría, es momento de poner a prueba tus habilidades. A continuación, encontrarás una serie de ejercicios prácticos que te ayudarán a afianzar tus conocimientos sobre las funciones inversas y las restricciones de dominio. ¡Intenta resolverlos por tu cuenta antes de ver las respuestas!
Ejemplo#1. Hallar la función inversa de
$$f(x)=2x-3$$
Solución
Primero. Es una función afín por lo tanto es biyectiva.
Segundo. Igualar f ( x ) = y.
$$y=2x-3$$
Tercero. Despejar x.
$$y=2x-3$$
$$2x=3+y$$
$$x=\frac{3+y}{2}$$
Cuarto. Intercambiar x por y.
$$y=\frac{3+x}{2}$$
Quinto. Sustituir “y” por f -1( x ).
$$f^{-1}(x)=\frac{3+x}{2}$$
Ejemplo#2. Determinar la función inversa de
$$f(x)=e^{x}$$
Solución
Paso 1: Verificar si es biyectiva.
Se determina si la función es inyectiva
$$f(x_{1})=f(x_{2})$$
$$f(x)=e^{x}$$
$$e^{x_{1}}=e^{x_{2}}$$
$$ln(e^{x_{1}})=ln(e^{x_{2}})$$
$$x_{1}=x_{2}$$
La función es inyectiva.
No es sobreyectiva porque, al calcular el rango, se observa que no coincide con el codominio. Rango$$y> 0$$
Aquí el rango es un subconjunto del codominio.
Paso 2: Se restringe el codominio para que sea igual al rango.
codominio restringido: $$y> 0$$
Paso 3: f ( x ) = y
$$y=e^{x}$$
Paso 4: Despejar x.
$$x=ln(y)$$
Paso 5: Intercambio de x por y.
$$y=ln(x)$$
Paso 6: “y” por f -1( x )
$$f^{-1}(x)=ln(x)$$
Ejemplo#3. Consigue la función inversa de
$$f(x)=x^{2}$$
Solución
Uno. Verificar si es biyectiva.
Determinar analíticamente si la función es inyectiva.
$$f(x_{1})=f(x_{2})$$
$$f(x)=x^{2}$$
$$x_{1}^{2}=x_{2}^{2}$$
$$x_{1}=\sqrt{x_{2}^{2}}$$
$$x_{1}=\pm x_{2}$$
La función no es inyectiva porque dos valores de entrada distintos pueden dar el mismo valor de salida.
La función no es sobreyectiva ya al determinar el rango$$y\geq 0$$
Dos. Se aplica restricción al dominio.
Dominio restringido:$$x> 0$$
Tres. Restricción al codominio.
codominio restringido: $$y\geq 0$$
Para igualarlo al rango.
Cuatro. f ( x ) = y
$$y=x^{2}$$
Quinto. Despejar x .
$$x=\sqrt{y}$$
Sexto. Intercambiar x por y.
$$y=\sqrt{x}$$
Séptimo. Cambiar “y” por f -1( x ).
$$f^{-1}(x)=\sqrt{x}$$
Funciones trigonométricas inversas
Las funciones trigonométricas no tienen una función inversa porque, al ser periódicas, sus valores se repiten. Esta característica impide que sean inyectivas (uno a uno) y, por lo tanto, no cumplen con el requisito fundamental para tener una función inversa.
Pero se le aplica restricciones en ciertos intervalos para que la función quede inyectiva, y en esos intervalos define una función inversa.
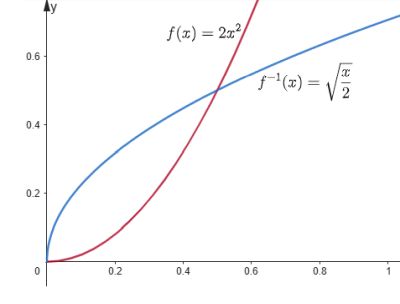
La imagen muestra la función$$f(x)=2x^{2}$$ restringida en el dominio (0,∞) y su inversa$$f^{-1}(x)=\sqrt{\frac{x}{2}}$$
Escritura y lectura de las funciones trigonométricas inversas
Leer y escribir las funciones trigonométricas inversas es sencillo, cuando trabajas con estos tipos de funciones, es relevante escribirlas correctamente para evitar confusiones. Hay dos maneras comunes de escribir y leerlas. A continuación, te muestro cada de ellas:
seno se escribe:$$sen^{-1}x$$Se lee: seno inverso de x$$arcsenx$$Lectura: arcoseno de x.
El mismo procedimiento se aplica para todas las demás.»
⚠️Cuidado con esta escritura
Se debe tener en cuenta que:
![]()
![]()
![]()
![]()
Recomendaciones para graficar funciones trigonométricas inversas
Las primeras recomendaciones es que te asegures que tu calculadora esté configurada en radianes, limita el dominio y el rango de la función original para que sea biyectiva. Al graficar su inversa, verás que los ejes se invierten: el dominio de la función original se convierte en el rango de la inversa y el rango se convierte en el dominio. Aquí tienes más recomendaciones que, espero, te sean de gran ayuda.
- Dibujar el plano cartesiano.
- Establecer en el eje “x” una escala 1:1.
- Establecer en el eje “y” los ángulos en radianes.
- Crear la tabla de valores.
- Graficar cada par ordenado y trazar la curva.
Inversa de la función seno
El dominio de la función del seno es el conjunto de los números reales ![]() y su rango está comprendido por el intervalo [-1,1].
y su rango está comprendido por el intervalo [-1,1].
Como se dijo anteriormente, las funciones trigonométricas son periódicas entonces no son inyectivas, pero quiero que veas que al aplicarle el criterio de la recta horizontal a la función seno se puede apreciar gráficamente que no es inyectiva ya que la recta toca en más de 1 punto.
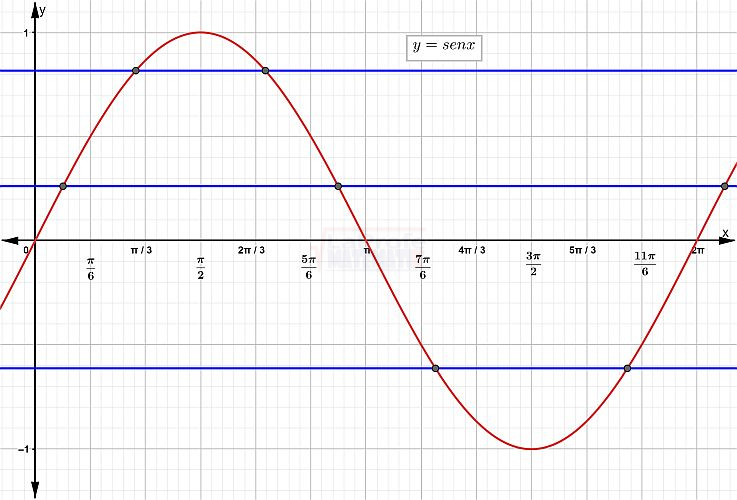
Entonces no es biyectiva.
Al no ser biyectiva la función seno no permite inversa en todo el conjunto de los números reales.
Aquí es donde se aplica la restricción con la única intención que la función seno permita inversa, el intervalo a restringir es ![]() su nuevo dominio, y el rango se limita al intervalo [-1,1] es aquí donde la función seno es biyectiva, y por lo tanto, admite una función inversa llamada arcoseno. Ver la imagen de la gráfica de la función seno con la restricción.
su nuevo dominio, y el rango se limita al intervalo [-1,1] es aquí donde la función seno es biyectiva, y por lo tanto, admite una función inversa llamada arcoseno. Ver la imagen de la gráfica de la función seno con la restricción.
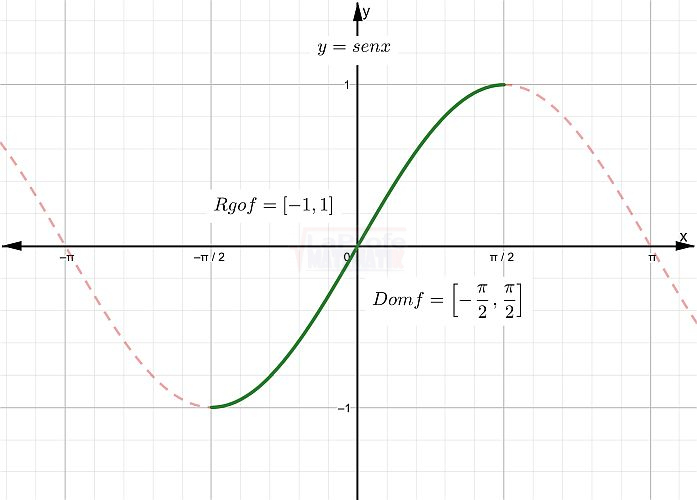
La inversa de la función seno, es la función que asigna un valor al ángulo cuando se tiene el valor del seno. sen x = y ⇒ arcsen y = x Su dominio es [-1,1] Su rango es: |
Entonces la interpretación de la definición del arcoseno de un valor x como el ángulo y en el intervalo ![]() tal que el seno del ángulo es x
tal que el seno del ángulo es x
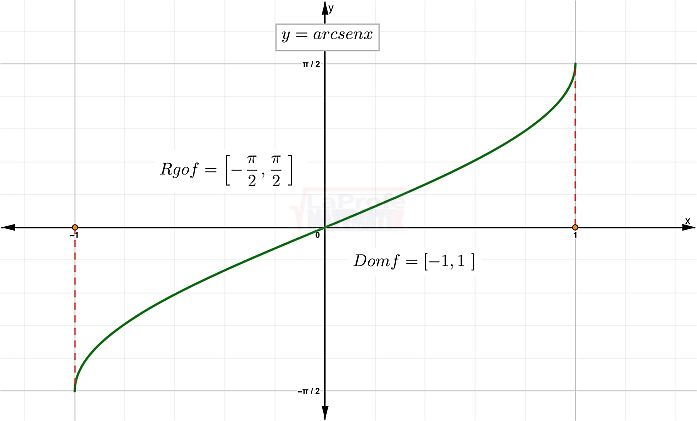
Gráfica de la función arcoseno
Ha llegado el momento de graficar la función del arcoseno, 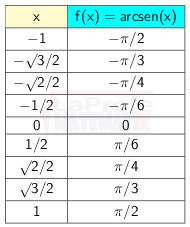 Allí tienes la tabla de valores, te recuerdo que el dominio está comprendido en el intervalo [-1,1]
Allí tienes la tabla de valores, te recuerdo que el dominio está comprendido en el intervalo [-1,1]
Observa que para x = 1/2
![]()
El ángulo obtenido en radianes es ![]() y en grados sexagesimales es 30°
y en grados sexagesimales es 30°
Al graficar cada par ordenado generado por la tabla de valores, se obtiene la curva de la función arcoseno.
🔭Observación: Si tu profesor no te permite usar calculadora, es porque el ejercicio se resuelve con ángulos notables. Haz clic aquí y te mostraré un truco matemático que te permitirá resolverlos sin necesidad de calculadora.
Relación entre la función seno y la función arcoseno
La relación entre la función seno y la función arcoseno, es que la función seno toma un ángulo para dar un valor entre -1 y 1, el arcoseno hace lo contrario: toma un valor entre -1 y 1 para darte el ángulo correspondiente.
Por esta razón, el dominio del arcoseno es el rango del seno, y el rango del arcoseno es el dominio restringido del seno.
| Función seno con restricción | Función arcoseno | |
| Intervalo en el dominio eje “x” | ||
| Intervalo en el rango eje “y” |
Características de la función arcoseno
- El dominio es el intervalo [ -1, 1]
- El rango es el intervalo [π/2, -π/2]
- No es periódica
- Es una función impar. Es decir, es simétrica respecto al origen del plano cartesiano.
- Valor máximo es = π/2 (90°) cuando x = 1.
- Valor mínimo = -π/2 (-90°) cuando x = -1.
- Valor donde la función corta al eje x e y es en el origen del plano cartesiano. Es decir, x = 0; y = 0.
Inversa de la función coseno
La función del coseno su dominio es también el conjunto de los números reales ![]() y el rango es el intervalo [-1,1].
y el rango es el intervalo [-1,1].
La función coseno es periódica por lo tanto no es inyectiva y por ende tampoco biyectiva.
Se aplica la restricción al dominio en el intervalo ![]() la cual le corresponde un rango de [-1,1], y el nombre de esta función inversa del coseno es llamada arcocoseno. Ver la gráfica de la función coseno con restricción en el dominio.
la cual le corresponde un rango de [-1,1], y el nombre de esta función inversa del coseno es llamada arcocoseno. Ver la gráfica de la función coseno con restricción en el dominio.
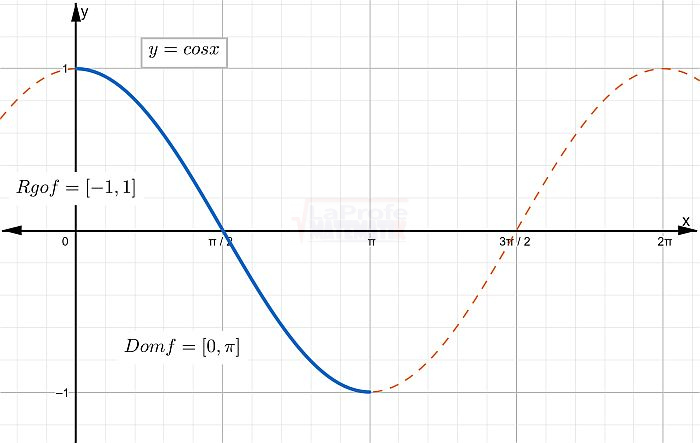
La inversa de la función coseno, permite determinar el ángulo conocido el valor del coseno. cosx = y ⇒ arccos y = x Su dominio es [-1,1] Su rango es: [0,π]. |
Relación entre la función coseno y la función arcocoseno
| Función coseno con restricción | Función arcocoseno | |
| Intervalo en el dominio eje “x” | ||
| Intervalo en el rango eje “y” |
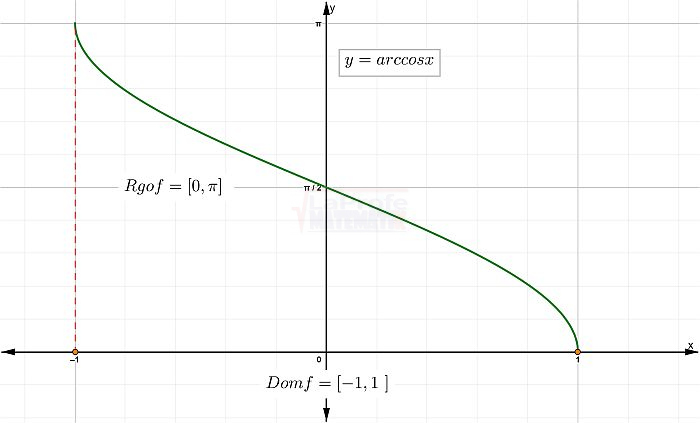
Gráfica de la función arcocoseno
Al igual que la función arcoseno se realiza la tabla de valores y el dominio usado para la variable independiente es el intervalo [-1,1]. Observa la gráfica de la función arcocoseno.
Características de la función arcocoseno
- El dominio es [ -1, 1].
- El rango es el intervalo
 .
. - No es periódica.
- No es una función par ni impar.
- Valor máximo o altura máxima es π cuando x = -1.
- Valor minino es 0 cuando x = 1.
- La función corta al eje y en π/2, cuando x = 0.
Inversa de la función tangente
Para definir la función tangente inversa, se debe restringir el dominio de la función tangente al intervalo ![]() y su rango quedaría como el conjunto de los números reales Rgo
y su rango quedaría como el conjunto de los números reales Rgo ![]() . Observe la gráfica con restricción en el dominio.
. Observe la gráfica con restricción en el dominio.
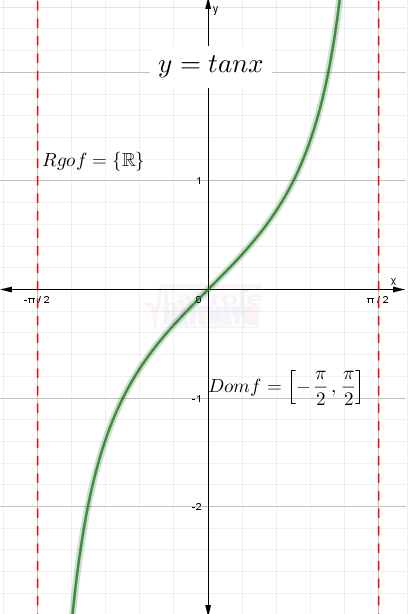
| La inversa de la función tangente, permite determinar el ángulo conocido el valor de la tangente. tan x = y ⇒ arctan y = x Su dominio es el conjunto de los números reales Su rango es: |
Relación entre la función tangente y la función arcotangente
| Función tangente con restricción | Función arcotangente | |
| Intervalo del dominio eje “x” | ||
| Intervalo del rango eje “y” |
Gráfica de la función arcotangente
Para realizar el gráfico de la función arcotangente, lo primero es realizar la tabla de valores y el dominio usado para la variable independiente es el conjunto de los ![]() . Observe la gráfica
. Observe la gráfica
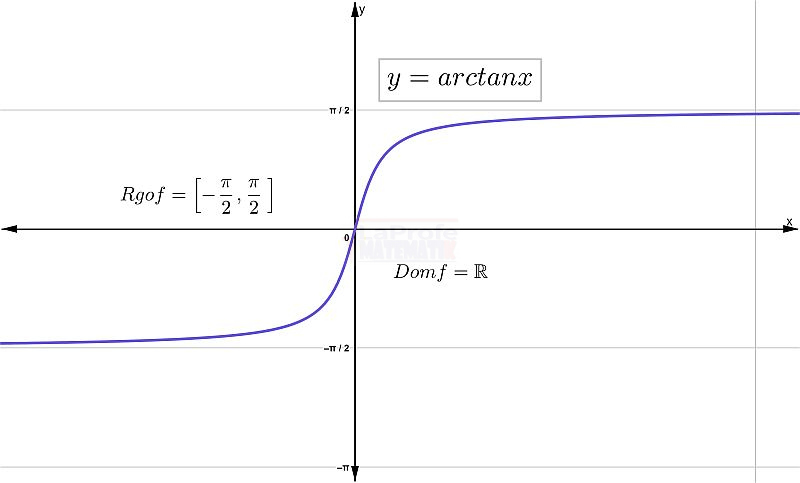
Características de la función arcotangente
- El dominio es
 .
. - El rango es el intervalo

- No es periódica.
- Es una función impar.
- No tiene valores máximos ni mínimos.
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
I. Construye la gráfica de la función arcotangente, los ángulos de la tabla de valores debe estar expresada en radianes. Usa estos valores para la variable independiente
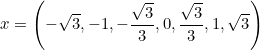
Recomendación: trabaja todo en grados sexagesimales, luego lo transforma a radianes.
II. Construya la gráfica del arcocoseno, los ángulos de la tabla de valores debe estar expresada en radianes. Los valores que vas a utilizar para la variable independiente son:
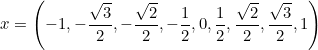
Recomendación: trabaja todo en grados sexagesimales, luego lo transforma a radianes.
III. Determina el valor exacto de cada ejercicio. Debes expresarlo en radianes y en grados sexagesimales
![]()
![]()
![]()
![]()
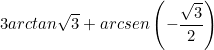
![]()
![]()
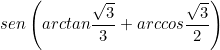
![]()
![]()
IV. Hallar el valor de x de las siguientes expresiones
![]()
![]()
![]()
![]()
![]()
![]()
V. Investiga las siguientes características de las funciones inversas:
¿Existen valores máximos y mínimos en la función del arcoseno? Si la respuesta es afirmativa indique las coordenadas?
¿La función arcoseno es biyectiva? y ¿Porqué?
¿Existen valores máximos y mínimos en la función del arcocoseno? Si la respuesta es afirmativa indica las coordenadas?
¿La función arcocoseno es sobreyectiva? y ¿Porqué?
¿Existen valores máximos y mínimos en la función del arcotangente? Si la respuesta es afirmativa indica las coordenadas?
¿La función arcotangente es sobreyectiva? y ¿Porqué?
