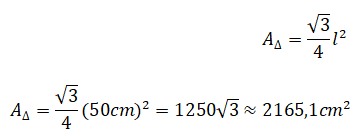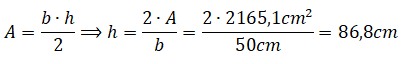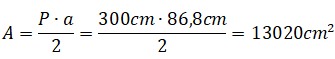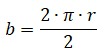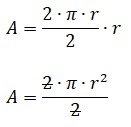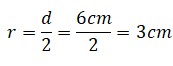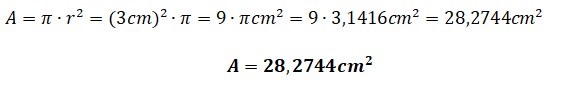La radicación es una operación matemática esencial que se utiliza tanto en aritmética como en álgebra.
La radicación es una operación matemática esencial que se utiliza tanto en aritmética como en álgebra.
Es la operación inversa de la potenciación: mientras la potenciación eleva un número a una potencia, la radicación busca un número que, al elevarlo a cierto exponente, dé como resultado otro número determinado.
En este post didáctico aprenderás qué son las propiedades de la radicación, cómo aplicarlas paso a paso y verás ejemplos concretos para que los puedas usar en tus estudios o explicaciones.
¿Qué es la radicación?
Antes que veas las propiedades, es bueno recordar que:
- La raíz n-ésima de un número a se escribe como $$\sqrt[n]{a}$$
- Significa encontrar un número que, elevado a la potencia n, da como resultado el radicando a.
Por ejemplo: $$\sqrt[3]{27}=3$$
Porque: $$3^{3}=27$$
Propiedades principales de la radicación
Las propiedades de la radicación son las siguientes:
1. Raíz de un producto.
2. Raíz de un cociente.
3. Raíz de una raíz.
4. Raíz de una potencia.
Raíz de un producto
La raíz de un producto es igual al producto de las raíces de cada factor. $$\sqrt[n]{a\cdot b}=\sqrt[n]{a}\cdot \sqrt[n]{b}$$
Ejemplo:
$$\sqrt[]{16\cdot 9}=\sqrt[]{16}\cdot \sqrt[]{9}=4\cdot 3=12$$
Esto simplifica cálculos cuando el radicando es producto de números con raíces exactas.
Raíz de un cociente
La raíz de una fracción es igual al cociente entre las raíces del numerador y del denominador.
$$\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=$$
Ejemplo: $$\sqrt[]{\frac{36}{4}}=\frac{\sqrt[]{36}}{\sqrt[]{4}}=\frac{6}{2}=3$$
Esta propiedad facilita simplificar raíces que contienen divisiones.
Raíz de una raíz
Si se calcula la raíz de una raíz, se puede simplificar multiplicando los índices.
$$\sqrt[m]{\sqrt[n]{a}}=\sqrt[m\cdot n]{a}$$
Ejemplo: $$\sqrt[4]{\sqrt[]{16}}=\sqrt[4\cdot 2]{16}=\sqrt[8]{16}$$
En forma de potencia queda así: $$16^{\frac{1}{8}}$$
Raíz de una potencia
Cuando una raíz está elevada a una potencia, se puede simplificar aplicando la relación entre radicación y potenciación.
Propiedad
La potencia de una raíz es igual a la raíz del radicando elevada a esa potencia:
$$\left ( \sqrt[n]{a} \right )^{m}=\sqrt[n]{a^{m}}$$
También puede interpretarse usando exponentes fraccionarios
$$\left ( \sqrt[n]{a} \right )^{m}=\left ( a^{\frac{1}{n}} \right )^{m}=a^{\frac{m}{n}}$$
Ejemplo 1: $$\left ( \sqrt{5} \right )^{2}=$$
Aplicar la propiedad
$$\left ( \sqrt{5} \right )^{2}= \sqrt{5^{2}}=5$$
Ejemplo 2: $$\left ( \sqrt[3]{2} \right )^{4}$$
Se expresa en forma de potencia: $$\left ( \sqrt[3]{2} \right )^{4}=\left ( 2^{\frac{1}{3}} \right )^{4}=2^{\frac{4}{3}}$$
Expresando en forma radical queda: $$2^{\frac{4}{3}}=\sqrt[3]{2^{4}}=\sqrt[3]{16}$$
Ejemplo 3: Con otro factor $$(3\sqrt{2})^{2}$$
Elevar cada factor al cuadrado $$(3\sqrt{2})^{2}=3^{2}\cdot (\sqrt{2})^{2}=9\cdot 2=18$$
ATENCIÓN
Esta propiedad no es válida si dentro del radical existe suma o resta: $$\sqrt{a+b}=\sqrt{a}+\sqrt{b}$$
Ejemplo de una situación incorrecta: $$\sqrt{25+9}=\sqrt{25}+\sqrt{9}=5+3=8$$
¿Para qué sirve la radicación?

La radicación sirve para que domines sus propiedades y puedas simplificar expresiones complejas, lo que te permitirá resolver problemas matemáticos con mayor claridad y fluidez.
Saber identificar cuándo aplicar estas propiedades —y cuándo no hacerlo, como ocurre en el caso de sumas o restas dentro de una raíz— es fundamental para construir un aprendizaje sólido en álgebra y en análisis matemático.
Las propiedades de la radicación no son reglas aisladas; tienen aplicaciones concretas en diferentes áreas de las matemáticas y las ciencias. Por ejemplo, se utilizan en:
- Simplificación de expresiones algebraicas.
- Resolución de ecuaciones que contienen raíces.
- Cálculo de longitudes y medidas en geometría.
- Modelos de crecimiento y decrecimiento en ciencias e ingeniería
Comprender la radicación no solo mejora tu manejo algebraico, sino que también fortalece tu capacidad de analizar y modelar situaciones reales.
Aprende las propiedades de la radicación fácil y rápido
Antes de comenzar con los ejercicios, te invito a ver el siguiente video donde se explica, de manera clara y progresiva, las propiedades de la radicación y cómo aplicarlas correctamente. A lo largo de mi experiencia enseñando matemáticas, he comprobado que comprender el “por qué” detrás de cada propiedad facilita enormemente la resolución de problemas y evita errores comunes, especialmente cuando trabajas con productos, cocientes y potencias dentro de raíces. Observa con atención cada paso y luego intenta resolver los ejemplos por tu cuenta.
En este video aprenderás cómo aplicar la raíz de un producto, cociente y potencia con ejemplos resueltos paso a paso para fortalecer tu comprensión.
Ahora que has visto la explicación, es momento de poner en práctica lo aprendido resolviendo los ejercicios siguientes.
Ejemplos explicados paso a paso aplicando las propiedades de la radicación
Los ejercicios a continuación, integran las propiedades de la radicación: producto, cociente, raíz de una raíz, potencia de una raíz y su relación con exponentes fraccionarios.
La clave está en identificar la propiedad adecuada antes de operar.
Raíz de un producto.
$$\sqrt{18}$$
Solución:
Antes de aplicar la propiedad, debes descomponer el número en factores y buscar cuadrados perfectos.
Para este caso que es el número 18
¿Qué números multiplicados dan 18?
¿Alguno de ellos es un cuadrado perfecto?
👉 Si aún te cuesta descomponer números, puedes apoyarte en la calculadora de descomposición para que veas el proceso paso a paso.
Usar la calculadora de descomposición
$$ 18 = 3^{2} \cdot 2 $$
$$ \sqrt{18} = \sqrt{3^{2} \cdot 2} = \sqrt{3^{2}}\cdot \sqrt{2} = 3\sqrt{2} $$
Raíz de un cociente.
$$\sqrt{\frac{49}{16}}=$$
Solución:
Descomposición en sus factores primos.
$$49=7^{2}\:\: y\: \: 16=2^{4}$$
$$ \sqrt{\frac{49}{16}} = \frac{\sqrt{7^{2}}}{\sqrt{2^{4}}} = \frac{7}{4} $$
Raíz de una raíz.
$$\sqrt{\sqrt[3]{64}}=$$
Solución:
Descomposición en sus factores primos al número 64.
$$64=2^{6}$$
$$ \sqrt{\sqrt[3]{64}} = \sqrt[6]{2^{6}} $$
Expresando en forma de potencia queda finalmente así:
$$=2^{\frac{6}{6}}=2$$
Raíz de una potencia.
$$(\sqrt{7})^2=$$
Solución:
$$ (\sqrt{7})^2 = 7 $$
Relación con exponentes fraccionarios.
$$\sqrt[4]{x^3}=$$
Solución:
Se expresa como potencia al ejercicio dado$$ \sqrt[4]{x^3} = x^{3/4} $$
Producto de radicales.
$$\sqrt{5}\cdot\sqrt{20} =$$
Solución:
$$ \sqrt{5}\cdot\sqrt{20} = \sqrt{100} = \sqrt{2^{2}\cdot 5^{2}}=10 $$
Radical con coeficiente y potencia.
$$(2\sqrt{3})^2=$$
Solución:
$$ (2\sqrt{3})^2 = 2^2\cdot \sqrt{3^{2}} = 4 \cdot 3 = 12 $$
Ejercicio combinado.
$$\sqrt{\frac{72}{2}}=$$
Solución:
Se divide el numerado y el denominador.
$$ \sqrt{\frac{72}{2}} = \sqrt{36} $$
Cuadrado perfecto de 36 es 6
$$ \sqrt{36} = 6 $$
Raíz y exponente combinado.
$$\left ( \sqrt[3]{8x^6}\right )^{2} =$$
Solución:
$$ \left ( \sqrt[3]{8x^6} \right )^{2} = \left ( \sqrt[3]{2^{3}\cdot x^{6}} \right )^{2}=$$
$$\sqrt[3]{2^{6}\cdot x^{12}}=2^{\frac{6}{3}}\cdot x^\frac{12}{3}=2^{2}\cdot x^{4}$$
$$=4\cdot x^{4}$$
Combinado completo.
$$\sqrt{12}\cdot\left ( \sqrt{3} \right )^{2} =$$
Solución:
$$\sqrt{12}\cdot\left ( \sqrt{3} \right )^{2} =$$
$$ = \sqrt{4\cdot3}\cdot 3 =\sqrt{2^{2}\cdot 3}\cdot 3 $$
$$ =2\sqrt{3}\cdot3$$
$$= 6\sqrt{3} $$
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
Parte # 1. Resuelva aplicando las propiedades de la radicación
| 1 | $$\sqrt[3]{-2\, 744}=$$ |
| 2 | $$\sqrt[5]{-32}=$$ |
| 3 | $$\sqrt{169\cdot 121}=$$ |
| 4 | $$\sqrt[3]{(-512)\cdot 343}=$$ |
| 5 | $$\sqrt[8]{(-5)^{16}}=$$ |
| 6 | $$\sqrt[12]{((-5)^{6})^{2}}=$$ |
| 7 | $$\sqrt[3]{(-5)^{12}\div (-5)^{6}}=$$ |
| 8 | $$\sqrt[4]{4^{8}\cdot 2^{12}\cdot 7^{4}}=$$ |
| 9 | $$\sqrt[5]{-256\cdot (-4)}=$$ |
| 10 | $$\sqrt{6\, 561\div 9}=$$ |
Parte # 2. Aplicar las propiedades de la radicación
| 1 | $$ \sqrt{\frac{128x^6}{2}}= $$ |
| 2 | $$ \left(\sqrt[3]{54a^6b^3}\right)^2 =$$ |
| 3 | $$ \sqrt[4]{\frac{81x^8}{16y^4}}= $$ |
| 4 | $$ \sqrt{50x^3}\cdot \sqrt{8x} =$$ |
| 5 | $$ \sqrt[3]{\sqrt{729x^9}} =$$ |
Respuestas:
Parte # 1:
| 1 | -14 |
| 2 | -2 |
| 3 | 143 |
| 4 | -56 |
| 5 | 25 |
| 6 | 5 |
| 7 | 25 |
| 8 | 448 |
| 9 | 4 |
| 10 | 27 |
Parte II:
| 1 | $$ 8x^3 $$ |
| 2 | $$ 9a^4b^2\sqrt[3]{4} $$ |
| 3 | $$ \frac{3x^2}{2y} $$ |
| 4 | $$ 20x^2\sqrt{x} $$ |
| 5 | $$ 3x^{3/2} $$ |
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión


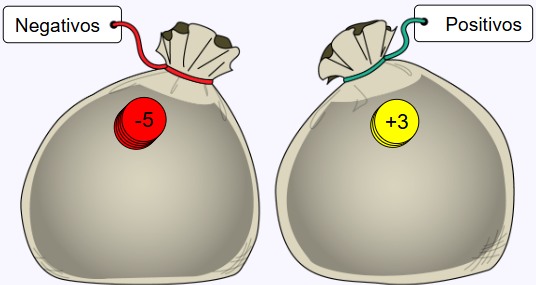
 Si quieres aprender los números enteros con simulaciones interactivas has llegado al lugar indicado. Los números enteros son de gran utilidad en nuestra vida cotidiana y están presentes en muchos aspectos de nuestras vidas.
Si quieres aprender los números enteros con simulaciones interactivas has llegado al lugar indicado. Los números enteros son de gran utilidad en nuestra vida cotidiana y están presentes en muchos aspectos de nuestras vidas.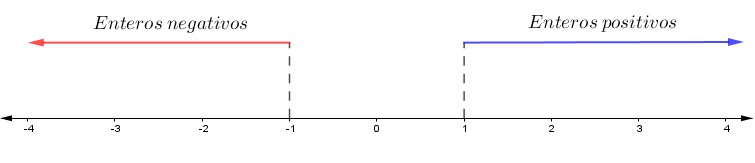
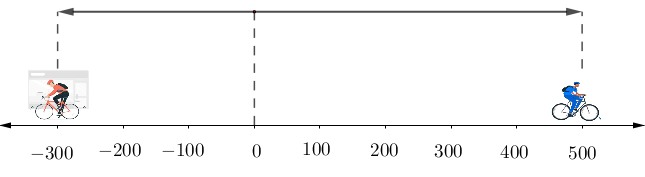
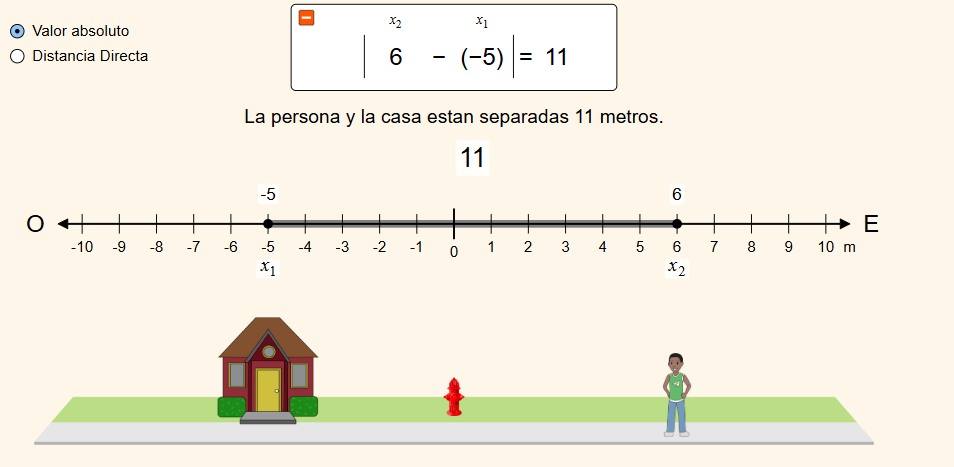







 Antes que veas la definición de la adición de dos números enteros de igual signo, es importante que sepas que en cualquier situación que involucre desplazamientos dirigidos hacia el este, o al oeste deben sumarse porque marchan hacia una misma dirección.
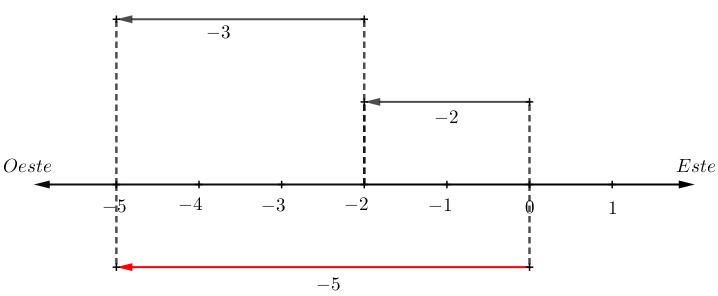
Antes que veas la definición de la adición de dos números enteros de igual signo, es importante que sepas que en cualquier situación que involucre desplazamientos dirigidos hacia el este, o al oeste deben sumarse porque marchan hacia una misma dirección.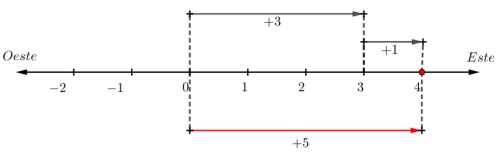
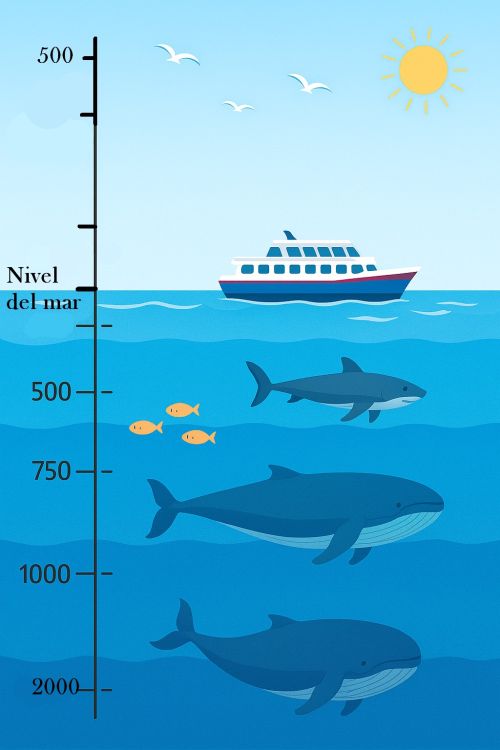

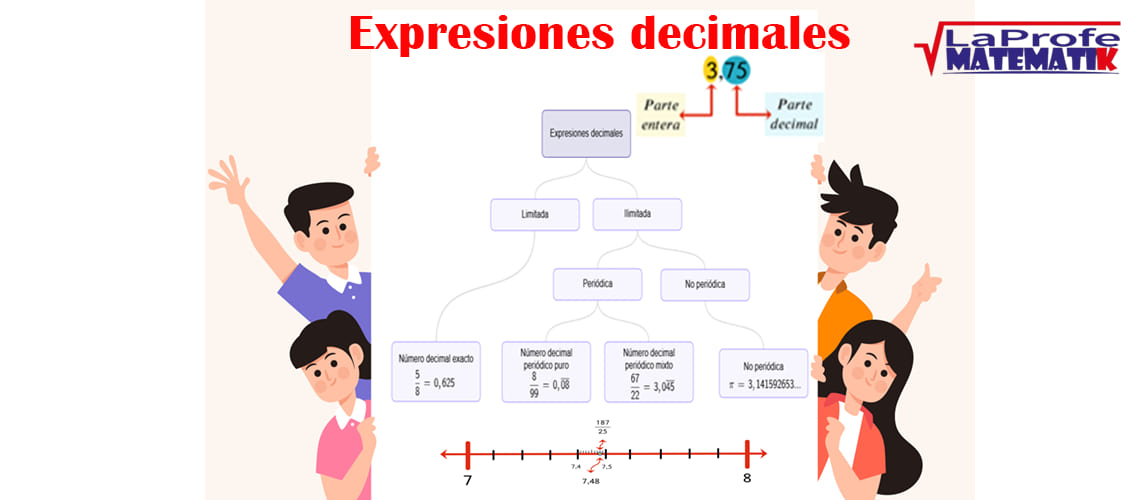
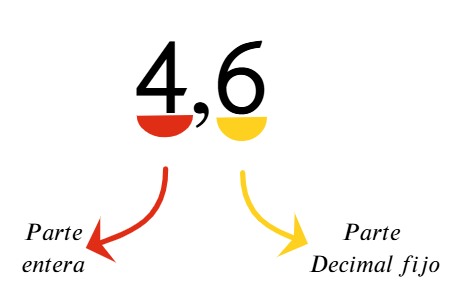
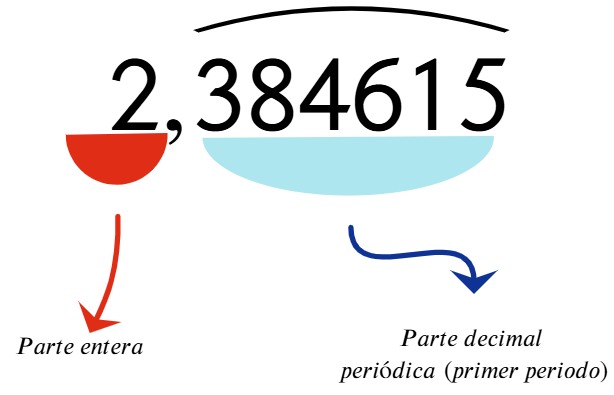
 ¿Alguna vez te has preguntado por qué en el colegio insisten tanto con fracciones y expresiones decimales, si en tu día a día lo que ves son precios, medidas, porcentajes o números en la pantalla del celular?
¿Alguna vez te has preguntado por qué en el colegio insisten tanto con fracciones y expresiones decimales, si en tu día a día lo que ves son precios, medidas, porcentajes o números en la pantalla del celular?

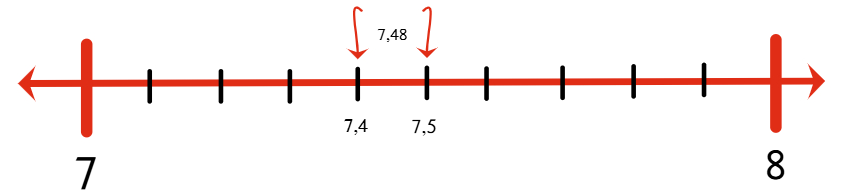
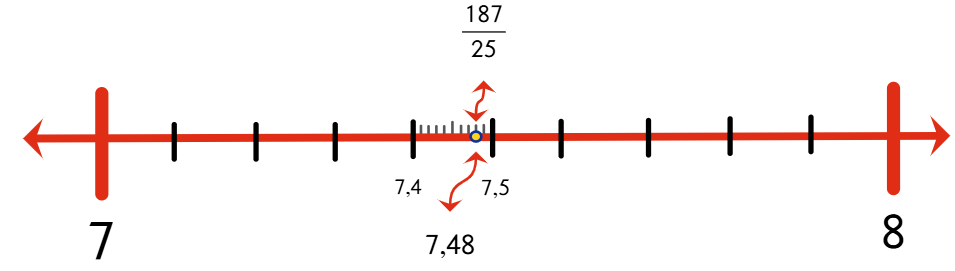
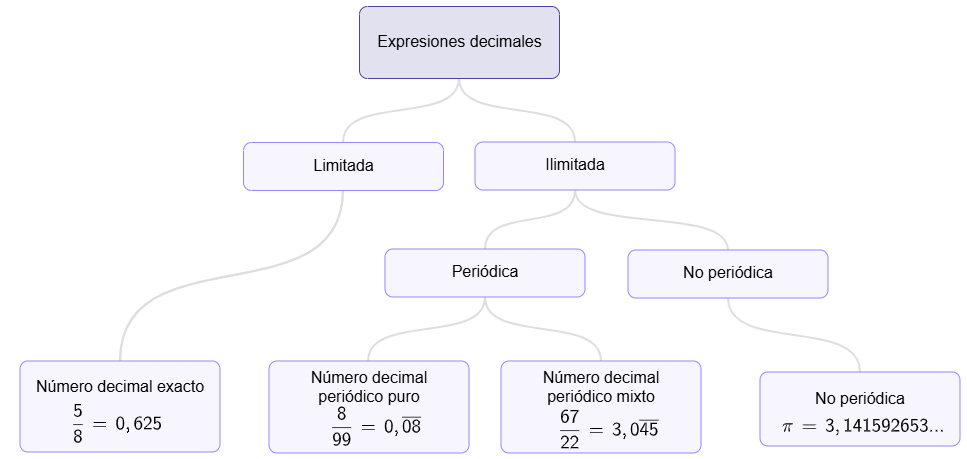
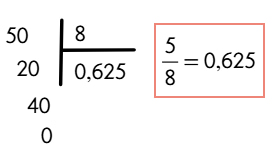
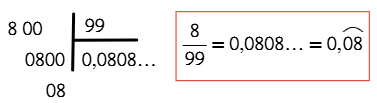



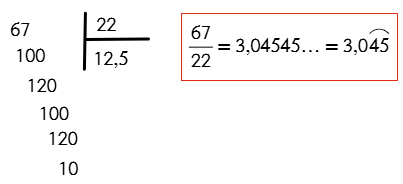
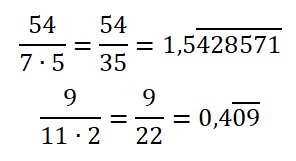


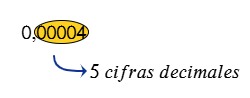
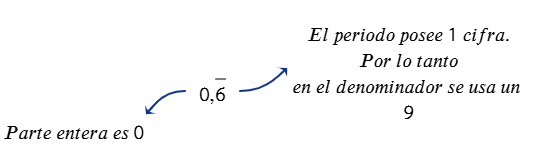
 ¿Alguna vez has intentado convertir un decimal a fracción y terminas con ganas de fraccionar tu cuaderno en mil pedacitos? 😂
¿Alguna vez has intentado convertir un decimal a fracción y terminas con ganas de fraccionar tu cuaderno en mil pedacitos? 😂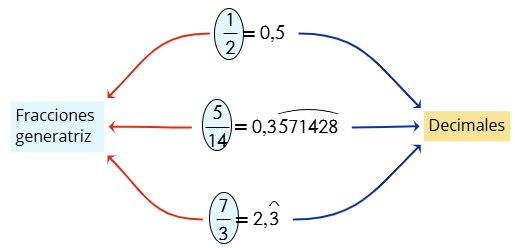
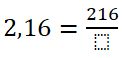

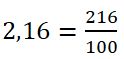
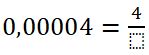
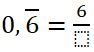
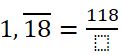
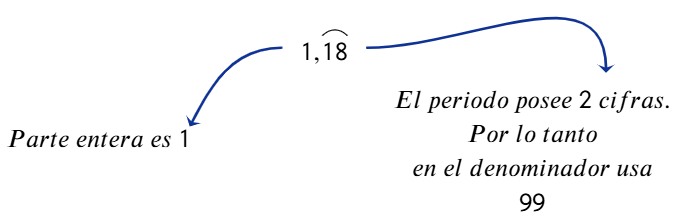

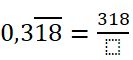
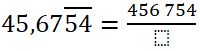
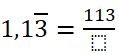
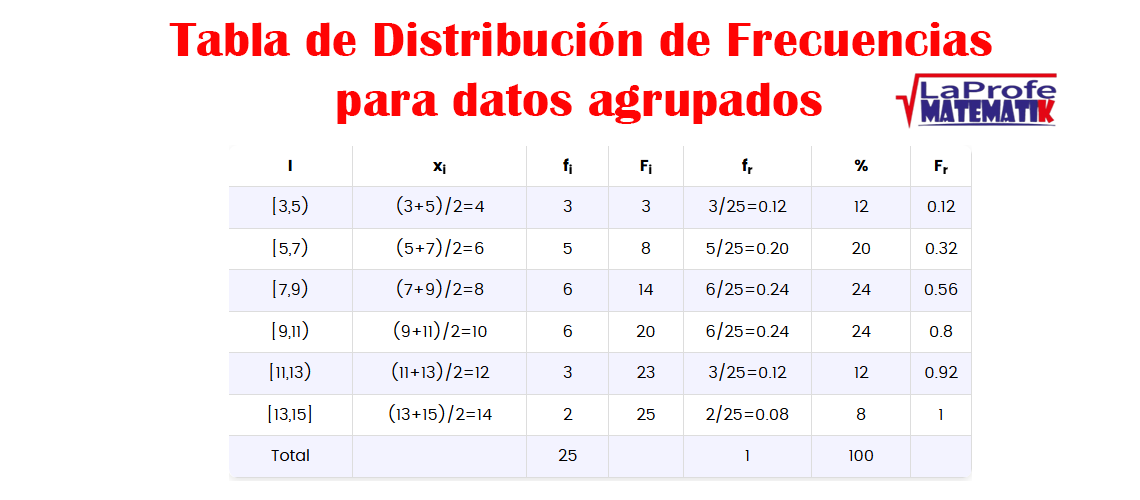
 ¿Alguna vez te has preguntado cómo construir tablas de frecuencias para datos agrupados y para qué sirven realmente en tu vida diaria?
¿Alguna vez te has preguntado cómo construir tablas de frecuencias para datos agrupados y para qué sirven realmente en tu vida diaria? Ejemplo. Construcción de una tabla de frecuencias para datos agrupados
Ejemplo. Construcción de una tabla de frecuencias para datos agrupados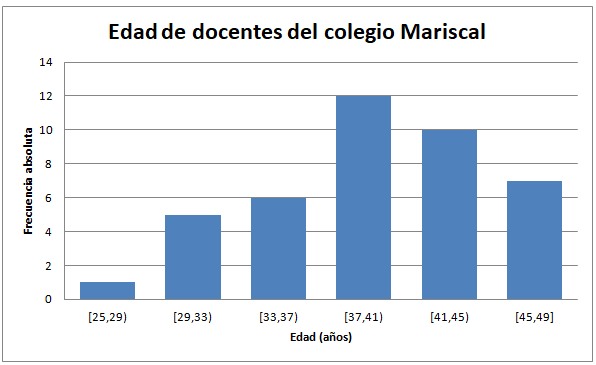

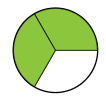
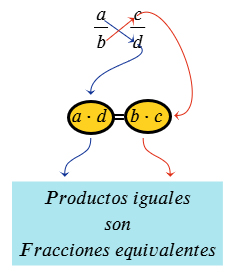
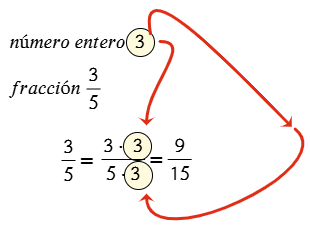
 ¿Sabías que usas fracciones todos los días sin darte cuenta? Las fracciones no solo están en las clases de matemáticas, también aparecen cuando juegas, compartes en redes sociales o ves tus series favoritas. Por ejemplo: al completar 3 de 4 misiones en un videojuego, ¡has avanzado las tres cuartas partes del reto! Y si 250 de tus 1.000 seguidores ven tu historia, eso significa que ¼ del total la ha visto. Las fracciones pueden parecer abstractas, pero tienen aplicaciones todo el tiempo en la vida diaria.
¿Sabías que usas fracciones todos los días sin darte cuenta? Las fracciones no solo están en las clases de matemáticas, también aparecen cuando juegas, compartes en redes sociales o ves tus series favoritas. Por ejemplo: al completar 3 de 4 misiones en un videojuego, ¡has avanzado las tres cuartas partes del reto! Y si 250 de tus 1.000 seguidores ven tu historia, eso significa que ¼ del total la ha visto. Las fracciones pueden parecer abstractas, pero tienen aplicaciones todo el tiempo en la vida diaria.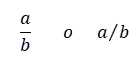

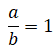
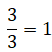
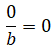

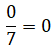
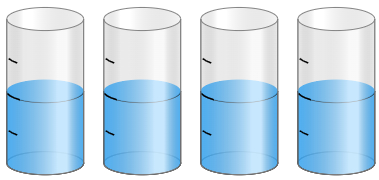
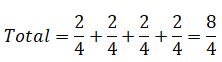
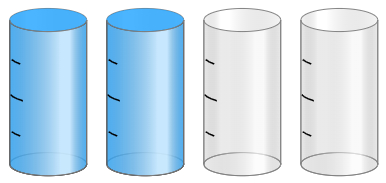
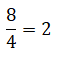 Todo número entero es múltiplo de 1, entonces, toda fracción cuyo denominador es 1 es también una fracción entera. Por ejemplo:
Todo número entero es múltiplo de 1, entonces, toda fracción cuyo denominador es 1 es también una fracción entera. Por ejemplo: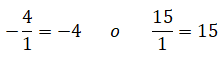

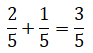
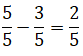
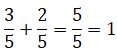


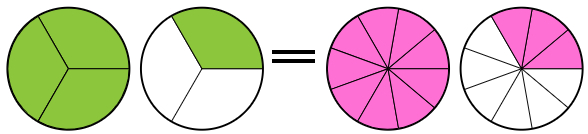

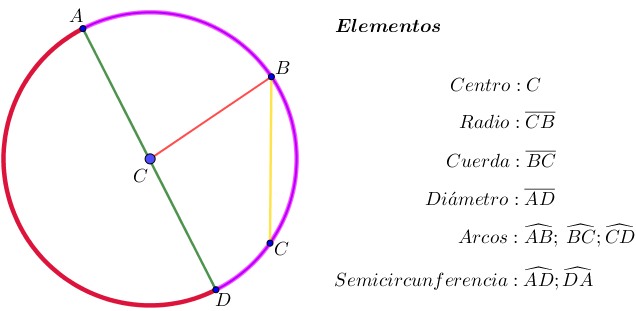
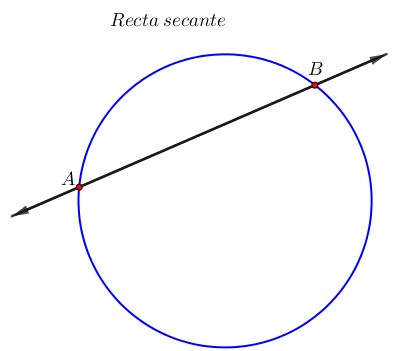
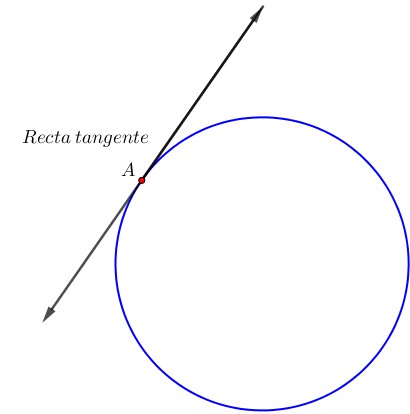
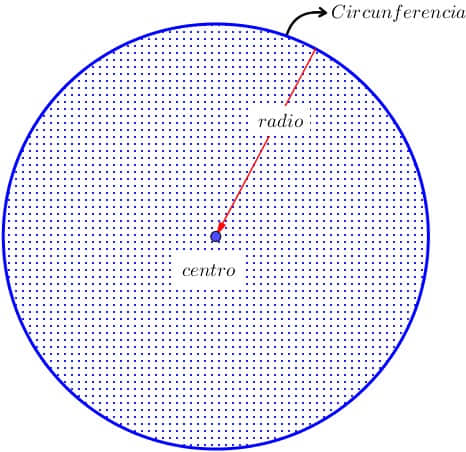
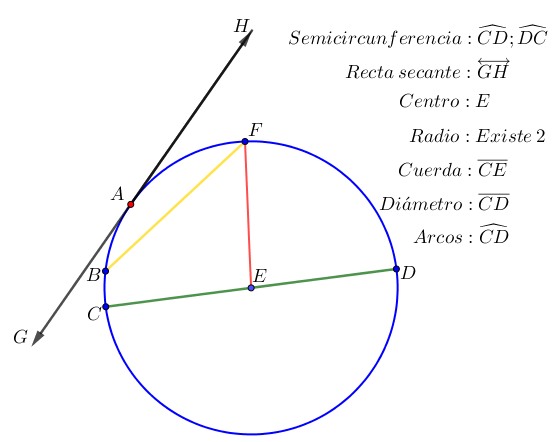
 ¿Quieres saber qué es la circunferencia y el círculo? Si es así, llegaste al lugar indicado. ¿Alguna vez has jugado FIFA, Rocket League o Minecraft? ¿Te gusta el básquet, el fútbol o lanzar discos voladores? En todos ellos, hay una figura matemática que aparece más de lo que crees: la circunferencia y el círculo. El balón de fútbol, el aro de básquet, los minimapas circulares de Fortnite o Call of Duty, o los escudos en Zelda todos usan esta forma geométrica. En este post conocerás sus elementos (como el centro, radio, diámetro, cuerda y otros) y también aprenderás cómo usarlos para construir y resolver problemas tanto en la vida diaria como en tus juegos favoritos.
¿Quieres saber qué es la circunferencia y el círculo? Si es así, llegaste al lugar indicado. ¿Alguna vez has jugado FIFA, Rocket League o Minecraft? ¿Te gusta el básquet, el fútbol o lanzar discos voladores? En todos ellos, hay una figura matemática que aparece más de lo que crees: la circunferencia y el círculo. El balón de fútbol, el aro de básquet, los minimapas circulares de Fortnite o Call of Duty, o los escudos en Zelda todos usan esta forma geométrica. En este post conocerás sus elementos (como el centro, radio, diámetro, cuerda y otros) y también aprenderás cómo usarlos para construir y resolver problemas tanto en la vida diaria como en tus juegos favoritos.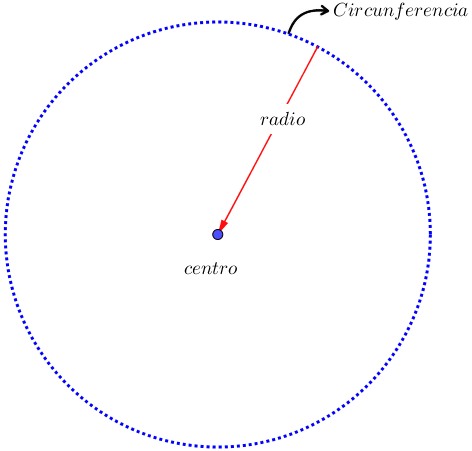


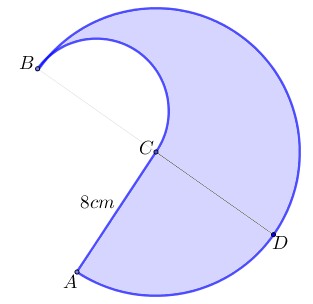
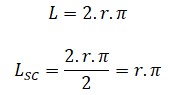
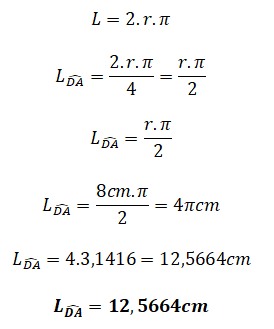
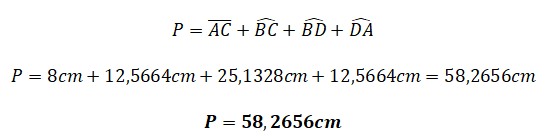


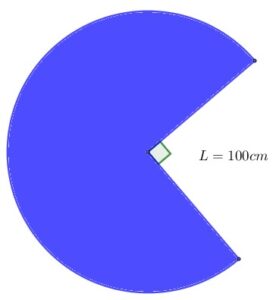

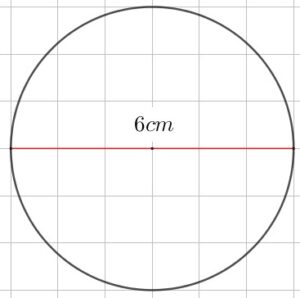
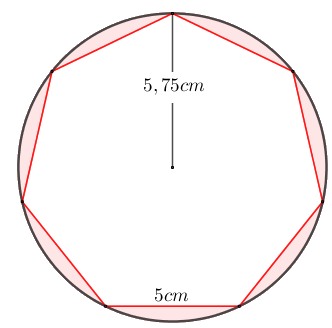
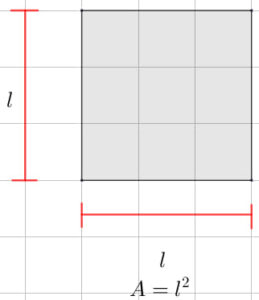
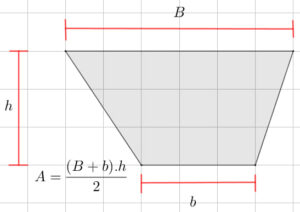
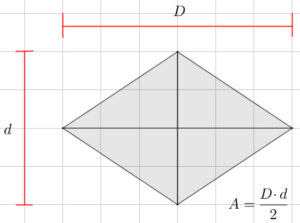
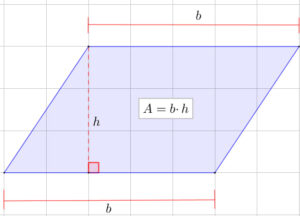
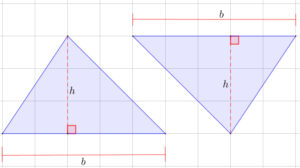
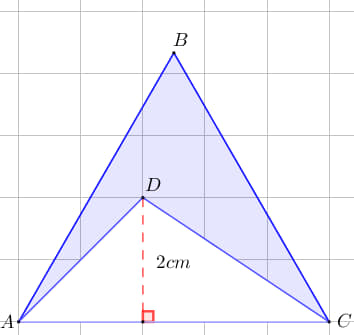
 ¿Estás buscando cómo calcular el área de cuadriláteros, triángulos, polígonos regulares y círculos? Si es así, has llegado al lugar indicado. ¿Sabías que calcular áreas no es solo cosa de matemáticas en clase? Cuando juegas fútbol, el campo tiene forma de rectángulo (¡un cuadrilátero!), en los videojuegos los mapas y zonas seguras tienen formas geométricas, y hasta los íconos que usas en redes sociales pueden ser círculos o polígonos. Profundiza en este tema y descubre cómo usar las fórmulas para hallar el área de triángulos, cuadriláteros, polígonos regulares y círculos.
¿Estás buscando cómo calcular el área de cuadriláteros, triángulos, polígonos regulares y círculos? Si es así, has llegado al lugar indicado. ¿Sabías que calcular áreas no es solo cosa de matemáticas en clase? Cuando juegas fútbol, el campo tiene forma de rectángulo (¡un cuadrilátero!), en los videojuegos los mapas y zonas seguras tienen formas geométricas, y hasta los íconos que usas en redes sociales pueden ser círculos o polígonos. Profundiza en este tema y descubre cómo usar las fórmulas para hallar el área de triángulos, cuadriláteros, polígonos regulares y círculos.


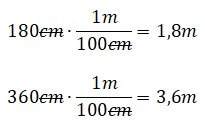
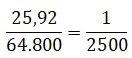

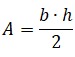
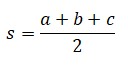

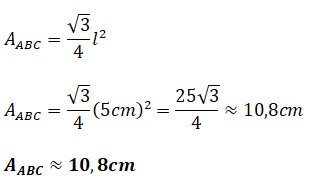
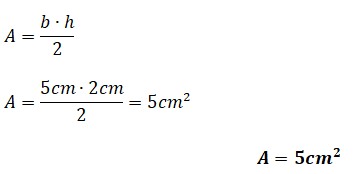
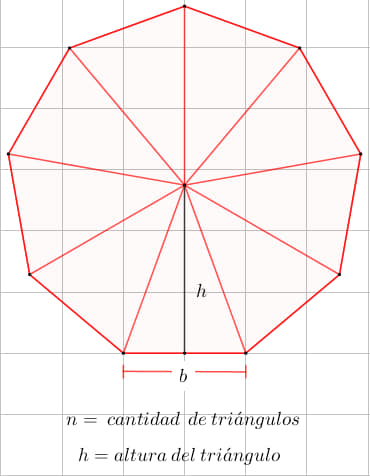
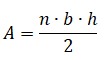
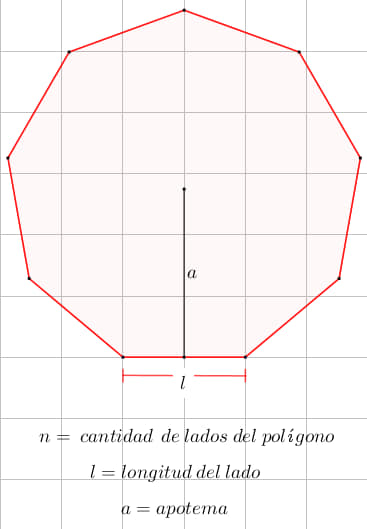
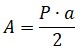
 El rector de una escuela está pensando en adquirir mesas para los estudiantes de primer grado, el área de esta mesa tiene forma hexagonal y cada lado mide 50cm. Calcula el área de la superficie para que el director tome la decisión de cuántas mesas debe comprar.
El rector de una escuela está pensando en adquirir mesas para los estudiantes de primer grado, el área de esta mesa tiene forma hexagonal y cada lado mide 50cm. Calcula el área de la superficie para que el director tome la decisión de cuántas mesas debe comprar.