En trigonometría, es muy común conocer únicamente una función trigonométrica de un ángulo y necesitar determinar las demás. Aunque al principio puede parecer un desafío, en realidad este proceso sigue una lógica clara basada en las relaciones matemáticas entre los lados de un triángulo rectángulo y las identidades fundamentales.
Dominar este procedimiento permite reconstruir toda la información trigonométrica de un ángulo a partir de un solo dato. Esta habilidad no solo es esencial en el ámbito académico, sino también en aplicaciones reales como el cálculo de alturas inaccesibles, el análisis de pendientes, la física del movimiento o el diseño de estructuras.
Además, este tema fortalece el razonamiento lógico, ya que el estudiante aprende a deducir información desconocida utilizando relaciones matemáticas precisas y confiables.
Cómo encontrar las demás funciones trigonométricas a partir de una función conocida
En muchos ejercicios, se proporciona una función trigonométrica —por ejemplo, el seno— y se solicita encontrar las demás:
- coseno
- tangente
- secante
- cosecante
- cotangente
Aunque existen varios enfoques, todos se basan en tres métodos fundamentales. La clave está en identificar cuál es el más adecuado según el tipo de información disponible.
Por qué es importante aprender este procedimiento
El dominio de este tema permite al estudiante:
- Resolver ejercicios de trigonometría con mayor seguridad.
- Comprender profundamente la relación entre los lados y los ángulos.
- Aplicar la trigonometría en problemas de física.
- Prepararse eficazmente para evaluaciones y exámenes.
- Desarrollar el razonamiento matemático y la capacidad de análisis.
En esencia, este conocimiento constituye una base indispensable para el estudio de la trigonometría.
Los tres métodos principales para encontrar las demás funciones trigonométricas
Existen tres métodos fundamentales:
- Método del triángulo rectángulo.
- Método de identidades trigonométricas.
- Método del círculo unitario.
Cada uno tiene aplicaciones específicas y niveles de complejidad diferentes.
Método 1: Triángulo rectángulo (método más visual y recomendado)
Este es el método más intuitivo y el más recomendado para comenzar. Se basa directamente en las definiciones de las funciones trigonométricas:
$$sen\beta =\frac{cateto\: opuesto}{hipotenusa}$$
$$cos\beta =\frac{cateto\: adyacente}{hipotenusa}$$
$$tan\beta =\frac{cateto\: opuesto}{cateto\: adyacente}$$
Cuándo utilizar este método
Este método es ideal cuando:
La función se presenta como una fracción.
El ejercicio involucra un triángulo rectángulo.
El nivel es básico o intermedio.
Ejemplo resuelto
Determinar las demás funciones trigonométricas si:$$\sin \beta = \frac{3}{5}$$
Solución:
Paso # 1: Interpretación la información.
$$\sin \beta = \frac{3}{5}=\frac{y}{r}=\frac{cateto\: opuesto}{hipotenusa}$$
Por lo tanto:
Cateto opuesto = 3
Hipotenusa = 5
Paso # 2: Calcular el cateto adyacente usando el teorema de Pitágoras.
$$r^{2}=y^{2}+x^{2}$$
Donde: r = hipotenusa; y = cateto opuesto; x = cateto adyacente
$$x=\sqrt{r^{2}-y^{2}}$$
$$x=\sqrt{5^{2}-3^{2}}$$
$$x=\sqrt{25-9}$$
$$x=4$$
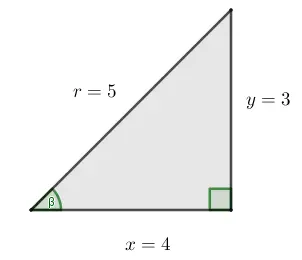
Paso # 3: Calcular las demás funciones
$$cos\beta =\frac{cateto\: adyacente}{hipotenusa}=\frac{4}{5}$$
$$tan\beta =\frac{cateto\: opuesto}{cateto\: adyacente}=\frac{4}{3}$$
$$csc\beta =\frac{r}{y}=\frac{5}{3}$$
$$sec\beta =\frac{r}{x}=\frac{5}{4}$$
$$cot\beta =\frac{x}{y}=\frac{4}{3}$$
Este método permite visualizar claramente el triángulo y reduce significativamente los errores.
Método 2: Identidades trigonométricas (método algebraico)
Este método se basa en el teorema de Pitágoras aplicado a un triángulo rectángulo. A partir de la expresión original, se divide toda la ecuación entre el cuadrado de la hipotenusa, entre el cuadrado del cateto adyacente y entre el cuadrado del cateto opuesto.
Como resultado de estas divisiones, se obtienen las identidades pitagóricas, las cuales forman parte de las identidades trigonométricas fundamentales y permiten calcular las demás funciones sin necesidad de construir el triángulo.
Observa el procedimiento:
$$\frac{r^{2}}{r^{2}}=\frac{y^{2}}{r^{2}}+\frac{x^{2}}{r^{2}}$$
$$\boxed{1=sen^{2}\beta +cos^{2}\beta } $$
$$\frac{r^{2}}{y^{2}}=\frac{y^{2}}{y^{2}}+\frac{x^{2}}{y^{2}}$$
$$\boxed { csc^{2}\beta =1 +cot^{2}\beta } $$
$$\frac{r^{2}}{x^{2}}=\frac{y^{2}}{x^{2}}+\frac{x^{2}}{x^{2}}$$
$$\boxed { sec^{2}\beta =tan^{2}\beta +1 } $$
Cuándo utilizar este método
Se recomienda cuando:
El ejercicio es algebraico.
No se desea dibujar un triángulo.
Aparecen expresiones más complejas.
Ejemplo resuelto
Si $$cos\beta =\frac{12}{13}$$
Solución:
Paso 1: Encontrar el seno.
$$sen^{2}\beta +cos^{2}\beta =1$$
$$sen^{2}\beta +\left ( \frac{12}{13} \right )^{2}=1$$
$$sen\beta =\sqrt{1-\frac{144}{169}}$$
$$sen\beta =\sqrt{\frac{25}{169}}$$
$$\boxed{sen\beta =\frac{5}{13}}$$
Paso 2: Encontrar la tangente.
$$tan\beta =\frac{sen\beta }{cos\beta }$$
$$tan\beta =\frac{\frac{5}{13}}{\frac{12}{13}}=\frac{5}{12}$$
$$\boxed{tan\beta =\frac{5}{12}}$$
Paso 3: Calcular las funciones recíprocas.
$$sec\beta =\frac{13 }{12 }$$
$$csc\beta =\frac{13 }{5 }$$
$$\boxed{cot\beta =\frac{12}{5 }}$$
Este método es especialmente útil en ejercicios de nivel intermedio y avanzado.
Método 3: Círculo unitario (método más completo)
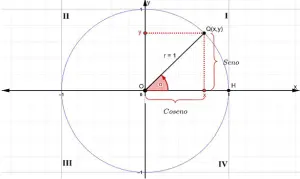El método del círculo unitario consiste en representar un ángulo en posición estándar dentro de un círculo de radio 1, centrado en el origen del plano cartesiano. Un ángulo está en posición estándar cuando su vértice se encuentra en el origen y su lado inicial coincide con el eje positivo de las x.
El lado terminal del ángulo corta la circunferencia en un punto cuyas coordenadas son (x, y). Este punto corresponde al extremo de un segmento que se extiende desde el origen hasta la circunferencia. Dicho segmento es el radio del círculo y, al mismo tiempo, representa la hipotenusa de un triángulo rectángulo imaginario formado con las proyecciones sobre los ejes coordenados.
Como el radio del círculo unitario mide 1, se cumple que:
$$cos\beta =x$$
$$sen\beta =y$$
$$tan\beta =\frac{y}{x}$$
Este ángulo puede ubicarse en cualquiera de los cuatro cuadrantes, lo que permite determinar los valores de las funciones trigonométricas para ángulos entre 0° y 360°, así como para ángulos negativos o mayores que una vuelta completa.
Cuándo utilizar este método
Es especialmente útil cuando:
Se conoce el cuadrante del ángulo.
El ángulo es negativo.
El ángulo es mayor de 90°.
Se requiere determinar el signo correcto.
Ejemplo resuelto
$$sen\beta =\frac{4}{5}$$
El ángulo se encuentra en el segundo cuadrante.
Solución:
Paso 1: Encontrar el coseno.
$$sen^{2}\beta +cos^{2}\beta =1$$
$$\left (\frac{4}{5} \right )^{2}+cos^{2}\beta =1$$
$$cos\beta =\sqrt{1-\frac{16}{25} }$$
$$cos\beta =\sqrt{\frac{9}{25}}$$
$$ cos\beta =\frac{3}{5}$$
Como está en el segundo cuadrante
$$\boxed{cos\beta =-\frac{3}{5}}$$
Paso 2: Encontrar la tangente.
$$tan\beta =\frac{sen\beta }{cos\beta }=\frac{\frac{4}{5}}{-\frac{3}{5}}=-\frac{4}{3}$$
$$\boxed{tan\beta =-\frac{4}{3}}$$
Paso # 3: Calcular las recíprocas.
$$\boxed{sec\beta =-\frac{5}{3}}$$
$$\boxed{csc\beta =\frac{5}{4}}$$
$$\boxed{cot\beta =-\frac{3}{4}}$$
Errores más comunes que se deben evitar
Evitar estos errores permite obtener resultados correctos con mayor facilidad.
Error 1: Aplicar incorrectamente el teorema de Pitágoras.
Un error frecuente consiste en calcular mal el lado faltante.
La fórmula correcta es:
$$hipotenusa^{2}=cateto\: opuesto^{2}+cateto\: adyacente^{2}$$
Error 2: Confundir las definiciones
Es fundamental recordar que:
$$sen\beta =\frac{cateto\: opuesto}{hipotenusa}$$
$$cos\beta =\frac{cateto\: adyacente}{hipotenusa}$$
$$tan\beta =\frac{cateto\: opuesto}{cateto\: adyacente}$$
Intercambiar estos valores produce resultados incorrectos.
Error 3: Olvidar las funciones recíprocas
Cada función tiene su recíproca correspondiente.
Error 4: No considerar el cuadrante
El signo depende del cuadrante.
Por ejemplo, si un ángulo está en el segundo cuadrante:
El seno es positivo.
El coseno es negativo.
- La tangente es negativa.
Ignorar esto conduce a respuestas incorrectas.
Error 5: No simplificar las fracciones
Siempre se debe expresar el resultado en su forma simplificada.
Por ejemplo:
$$\frac{6}{8}=\frac{3}{4}$$
Comparación de los tres métodos
Cada método tiene ventajas específicas. Elegir el adecuado permite resolver los ejercicios con mayor rapidez y precisión.
| Método | Ventajas | Limitaciones | Cuándo usarlo | Nivel recomendado |
Triángulo rectángulo | • Es el método más visual e intuitivo. • Facilita la comprensión del significado geométrico de las funciones. • Permite encontrar todas las funciones de forma ordenada. • Reduce la probabilidad de errores algebraicos. • Ideal para estudiantes que están aprendiendo trigonometría. | • Solo se puede aplicar directamente en triángulos rectángulos. • No se puede usar cuando el ángulo está fuera del primer cuadrante. • No es práctico en ejercicios puramente algebraicos. | • Cuando la función está en forma de fracción. • Cuando el ejercicio involucra triángulos rectángulos. • Cuando el ángulo es agudo. | Básico e intermedio |
Identidades trigonométricas | • Permite resolver ejercicios sin necesidad de dibujar triángulos. • Es útil en ejercicios algebraicos. • Funciona con cualquier valor numérico. • Es más rápido cuando se domina el procedimiento. • Es fundamental en matemáticas avanzadas. | • Puede generar errores algebraicos si no se domina bien. • No proporciona información visual. • No permite determinar el signo si no se conoce el cuadrante. | • Cuando el ejercicio es algebraico. • Cuando aparecen identidades trigonométricas. • Cuando no se trabaja con triángulos. | Intermedio |
Círculo unitario | • Permite determinar el signo correcto de cada función. • Funciona en los cuatro cuadrantes. • Es esencial para trigonometría avanzada. • Permite trabajar con ángulos negativos y mayores de $$90^\circ$$. • Proporciona una comprensión completa de las funciones trigonométricas. | • Es más abstracto y requiere mayor comprensión. • Puede resultar difícil para estudiantes principiantes. • Requiere conocer bien los signos por cuadrante. • No siempre es necesario en ejercicios básicos. | • Cuando el ejercicio menciona el cuadrante. • Cuando el ángulo puede ser negativo. • Cuando se requiere el signo correcto. | Intermedio y avanzado |
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades:
I. Aplicar el método del triángulo rectángulo.
| 1 | $$sin θ = \frac{5}{13}$$ |
| 2 | $$cos θ = \frac{8}{17}$$ |
| 3 | $$tan θ = \frac{7}{24}$$ |
II. Aplicar identidades trigonométricas.
| 1 | $$sin θ = \frac{12}{13}$$ |
| 2 | $$cos θ = \frac{9}{41}$$ |
| 3 | $$sin θ = \frac{20}{29}$$ |
III. Aplicar el círculo unitario.
| 1 | $$sin θ = \frac{3}{5}$$ | θ está en el segundo cuadrante. |
| 2 | $$cos θ = -\frac{12}{13}$$ | θ está en el tercer cuadrante. |
| 3 | $$tan θ = -\frac{8}{15}$$ | θ está en el cuarto cuadrante. |
Resultados:
| Triángulo rectángulo | |
| 1 | $$cos θ = \frac{12}{13}$$ |
| $$tan θ = \frac{5}{12}$$ | |
| $$csc θ = \frac{13}{5}$$ | |
| $$sec θ = \frac{13}{12}$$ | |
| $$cot θ = \frac{12}{5}$$ | |
| 2 | $$sin θ = \frac{15}{17}$$ |
| $$tan θ = \frac{15}{8}$$ | |
| $$csc θ = \frac{17}{15}$$ | |
| $$sec θ = \frac{17}{8}$$ | |
| $$cot θ = \frac{8}{15}$$ | |
| 3 | $$sin θ = \frac{7}{25}$$ |
| $$cos θ = \frac{24}{25}$$ | |
| $$csc θ = \frac{25}{7}$$ | |
| $$sec θ = \frac{25}{24}$$ | |
| $$cot θ = \frac{24}{7}$$ | |
| Identidades trigonométricas | |
| 1 | $$cos θ = \frac{5}{13}$$ |
| $$tan θ = \frac{12}{5}$$ | |
| $$csc θ = \frac{13}{12}$$ | |
| $$sec θ = \frac{13}{5}$$ | |
| $$cot θ = \frac{5}{12}$$ | |
| 2 | $$sin θ = \frac{40}{41}$$ |
| $$tan θ = \frac{40}{9}$$ | |
| $$csc θ = \frac{41}{40}$$ | |
| $$sec θ = \frac{41}{9}$$ | |
| $$cot θ = \frac{9}{40}$$ | |
| 3 | $$cos θ = \frac{21}{29}$$ |
| $$tan θ = \frac{20}{21}$$ | |
| $$csc θ = \frac{29}{20}$$ | |
| $$sec θ = \frac{29}{21}$$ | |
| $$cot θ = \frac{21}{20}$$ | |
| Círculo unitario | |
| 1 | $$cos θ = -\frac{4}{5}$$ |
| $$tan θ = -\frac{3}{4}$$ | |
| $$csc θ = \frac{5}{3}$$ | |
| $$sec θ = -\frac{5}{4}$$ | |
| $$cot θ = -\frac{4}{3}$$ | |
| 2 | $$sin θ = -\frac{5}{13}$$ |
| $$tan θ = \frac{5}{12}$$ | |
| $$csc θ = -\frac{13}{5}$$ | |
| $$sec θ = -\frac{13}{12}$$ | |
| $$cot θ = \frac{12}{5}$$ | |
| 3 | $$sin θ = -\frac{8}{17}$$ |
| $$cos θ = \frac{15}{17}$$ | |
| $$csc θ = -\frac{17}{8}$$ | |
| $$sec θ = \frac{17}{15}$$ | |
| $$cot θ = -\frac{15}{8}$$ | |
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión
Realicé dos ejercicios de practica, y me parecio muy bueno ya que, con las respuestas que me decian, podía ver si tenía un error y así arreglarlo. Me parecio muy interesante el tema.
Muchas gracias por tu comentario. Me alegra saber que los ejercicios y sus respuestas te ayudaron a identificar y corregir errores, fortaleciendo así tu aprendizaje. También es muy positivo que el tema haya sido de tu interés.
¡Te felicito por tu dedicación y te animo a seguir practicando!