¿Sabías que los Números Mixtos están detrás de las porciones de pizza de TikTok y de los bloques en Minecraft?
Alguna vez has jugado algún videojuego favorito, como Minecraft o Fortnite, y necesitas saber cuántos bloques tienes para construir esa mega-estructura o cuántas porciones te quedan si ya usaste la mitad? O tal vez están viendo videos en TikTok y alguien dice que necesita «una pizza y media» para su fiesta, o que un influencer mide «un metro y medio» de alto. ¡Pues déjame decirte que esas distintas situaciones se refieren a los Números Mixtos!
En este post aprenderás qué son exactamente, cómo pasar de un número mixto a una fracción impropia y viceversa. Además, reforzarás cada concepto con una simulación divertida que hará el aprendizaje mucho más fácil. ¡Prepárate para dominar esta herramienta matemática esencial!
¿Qué son los Números Mixtos?
| Es la composición de un número entero y una fracción propia. Su forma de escritura es la siguiente:
Donde: a es el número entero. b/c es la fracción propia.
|
Por ejemplo: María y sus amigas celebran el primer año de estar graduadas en ingeniería electrónica y decidieron ir a una pastelería para comer pastel, cada pastel fue cortado en tres partes iguales. Según la imagen ¿Qué cantidad comieron?
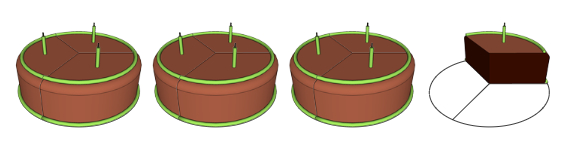
Respuesta: María y sus amigas comieron 3 pasteles y una porción de 1/3, es decir, 3 1/3.
¿Dónde se usan números mixtos?
 Los números mixtos se emplean con frecuencia en muchos momentos de la vida diaria, permite expresar cantidades de forma clara y sencilla. Por ejemplo:
Los números mixtos se emplean con frecuencia en muchos momentos de la vida diaria, permite expresar cantidades de forma clara y sencilla. Por ejemplo:
- Cuando una receta te solicita de tazas de azúcar.
- Si alguien te pregunta: ¿Qué hora es? y tú responde: son las
- La medida de una llave fija es de 1 ¾ pulgadas.
Conversión de fracción impropia a número mixto
Cuando una fracción el número de arriba denominado numerador es mayor que el número de abajo llamado denominador, se le llama fracción impropia. Ejemplo:
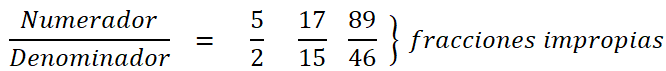
Solo este tipo de fracciones se pueden convertir en números mixtos y viceversa.
Para convertirlas debes cumplir con solo 5 pasos:
- Escribe la fracción impropia y coloca el signo igual.
- Divide el numerador entre el denominador.
- El número que obtienes como cociente es la parte entera del número mixto. Escríbelo a la derecha del signo igual.
- El número que queda como residuo se convierte en el numerador de la fracción del número mixto.
- El denominador sigue siendo el mismo que tenía la fracción impropia.
A continuación, te muestro 2 ejemplos resueltos:
Ejemplo # 1: Convertir la siguiente fracción impropia 17/3 a número mixto. Observa el procedimiento.
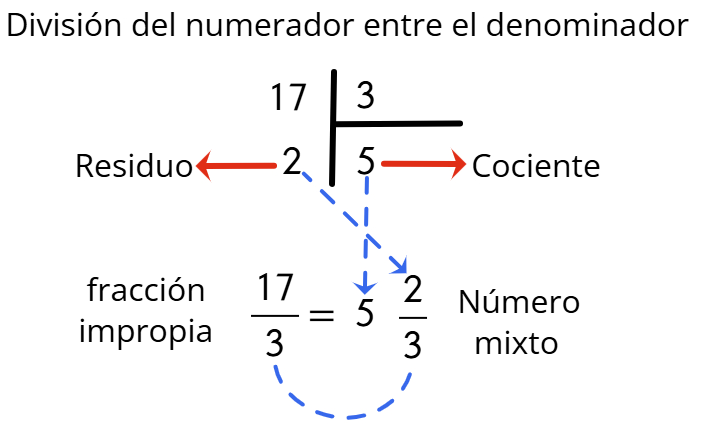
| Pasos | Operación |
| 1 | $$\frac{17}{3}=$$ |
| 3 | |
| 4 | |
| 5 | $$\frac{17}{3}=5\frac{2}{3}$$ |
Respuesta: $$\frac{17}{3}=5\frac{2}{3}$$
Ejemplo # 2: Convierte las siguientes fracciones impropias a números mixtos.
a) \(\frac{34}{5}=6\frac{4}{5}\)
b) \(\frac{65}{11}=5\frac{10}{11}\)
c) \(\frac{105}{23}=4\frac{13}{23}\)
d) \(\frac{525}{85}=6\frac{15}{85}\)
Conversión de número mixto a fracción impropia
Convertir un número mixto a fracción impropia es muy fácil, solo debes aplicar un procedimiento que contiene 3 pasos. Estos pasos son los siguientes:
1.Delante del número mixto escribe el signo igual.
2.Escribe el mismo denominador del número mixto para la fracción impropia.
3.Multiplica el número entero por el denominador y le sumas el numerador, el resultado es el numerador de la fracción impropia.
Ejemplo # 1: Convertir de número mixto a fracción impropia.
| Pasos | Operación |
| 1 | $$4\frac{5}{7}=$$ |
| 2 | |
| 3 | $$4\frac{5}{7}=\frac{33}{7}$$ |
Ejemplo # 2: Convierte los siguientes números mixtos a fracción impropia.
a) \(7\frac{2}{11}=\frac{79}{11}\)
b) \(3\frac{9}{15}=\frac{54}{15}=\frac{18}{5}\)
c) \(11\frac{3}{10}=\frac{113}{10}\)
d) \(9\frac{1}{3}=\frac{28}{3}\)
Graficar números mixtos
Hasta aquí ya te diste cuenta que las fracciones impropias y los números mixtos representan la misma cantidad, son dos formas distintas que significan lo mismo.
Los números mixtos permiten visualizar e interpretar cualquier situación de manera mucho más clara y rápida. A continuación, te muestro distintas situaciones graficadas para una mejor comprensión.
Ejemplo # 1: El jefe de Carlos le pide que llene de litros de agua a los envases cilíndricos, cada envase tiene una capacidad de 1 litro. ¿Qué cantidad de envases necesita Carlos?
El entero “1” del número mixto representa un cilindro lleno de líquido y la fracción son 2 porciones de 3. Observa la gráfica:
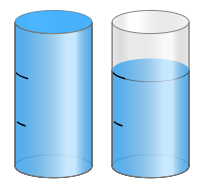
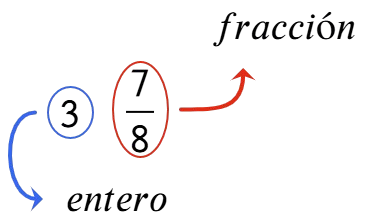
Ejemplo # 2: Observa la imagen y expréselo en número mixto.

Análisis
El envase está dividido en 8 partes iguales (representa el denominador).
Están llenos 3 envases.
El último envase se llenó hasta la parte 7 del envase (representado el numerador)
Respuesta:
$$3\frac{7}{8}=$$
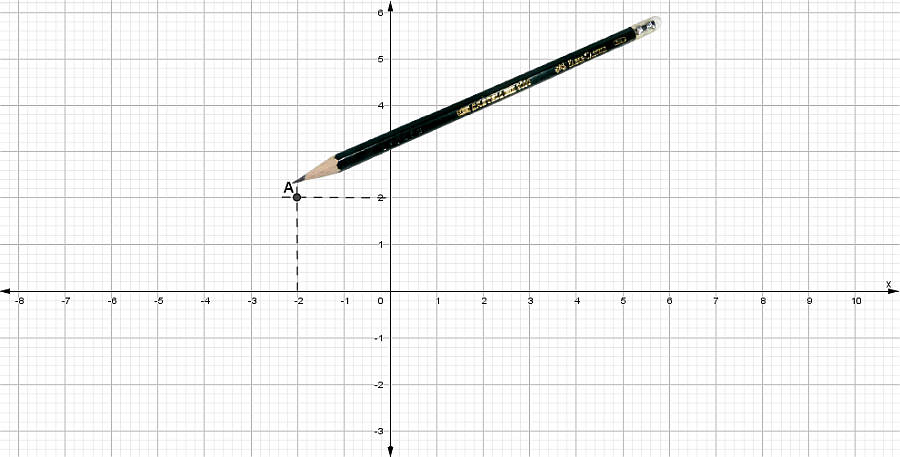
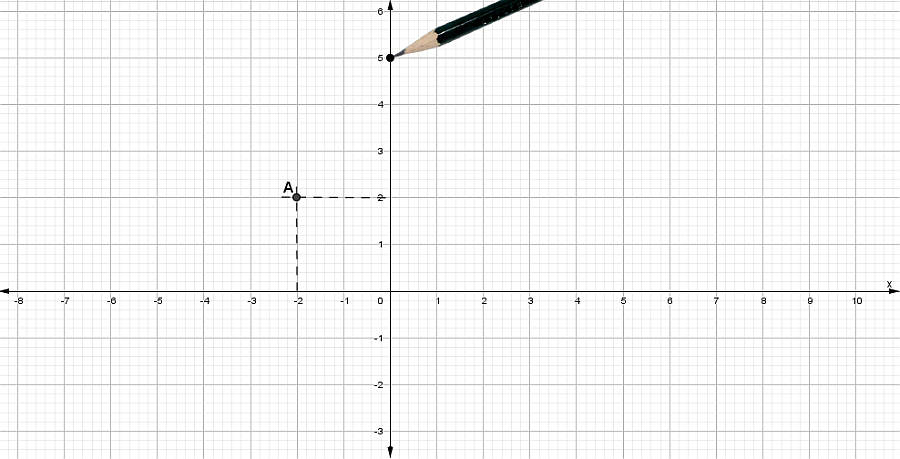
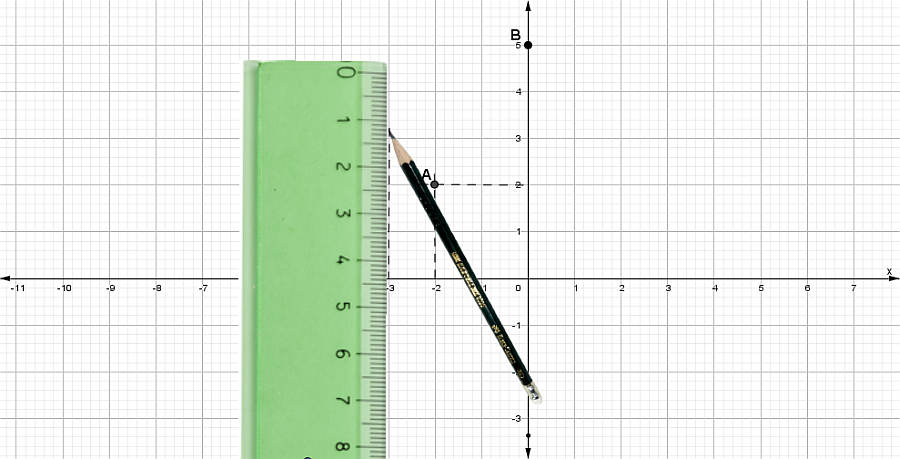
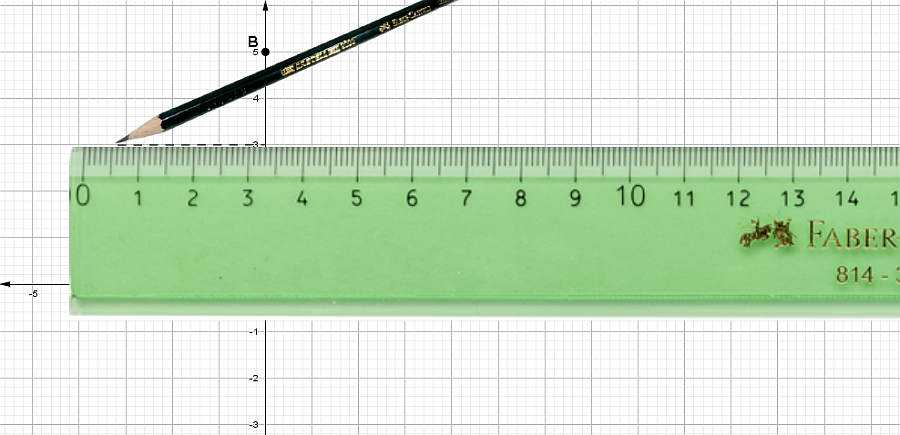
Ejemplo # 3: Juan está construyendo una repisa para su habitación. Al medir una de las tablas con un flexómetro (metro enrollable), se da cuenta que su longitud no es un número exacto. ¿Cuánto mide la tabla?
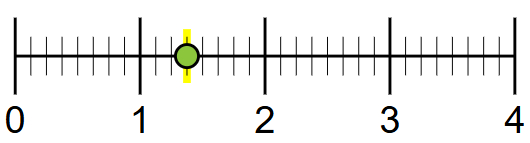
Respuesta: La longitud de la tabla es de \(1\frac{3}{8} metros\)
Aprende números mixtos en simulación
¡Es hora de poner a prueba lo aprendido! En este laboratorio de simulación, vas a construir números mixtos nivel a nivel. ¿Listo para el desafío? Te esperan 5 niveles para que domines este tema jugando. ¡Vamos a ello!
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
1.Escribe el número mixto en cada caso. Luego, exprésalo como fracción impropia.
| a |
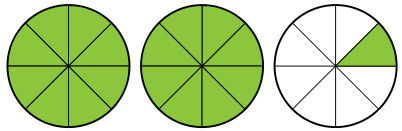 |
| Respuesta: _____ |
| b |
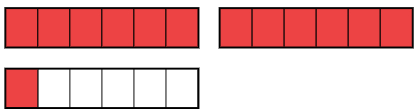 |
| Respuesta: _____ |
2.Convierte a números mixtos las siguientes fracciones.
| a) | 7/2 | d) | 21/13 |
| b) | 9/3 | e) | 22/6 |
| c) | 11/5 | f) | 14/7 |
3.Relaciona cada número mixto con su correspondiente fracción impropia.

4.Soluciona la siguiente situación:
Carlos y Valeria se propusieron leer el mismo libro de 200 páginas. Carlos ha leído todo el libro, mientras que Valeria ha leído 9/4 partes del libro. ¿Quién ha leído más? ¿Por qué?
Respuesta: Al transformar 9/4 a número mixto queda así: 2 ¼ , es decir, que Valeria ha leído más el libro que Carlos.


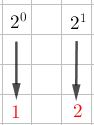
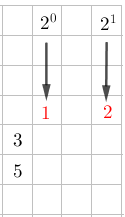
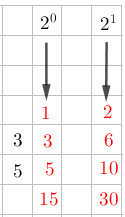
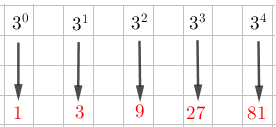
 ¿Alguna vez te has preguntado para qué sirven los divisores de un número en la vida real?
¿Alguna vez te has preguntado para qué sirven los divisores de un número en la vida real?




 ¿Te has preguntado alguna vez qué son realmente los polígonos y por qué los encontramos en tantas formas a nuestro alrededor?
¿Te has preguntado alguna vez qué son realmente los polígonos y por qué los encontramos en tantas formas a nuestro alrededor?
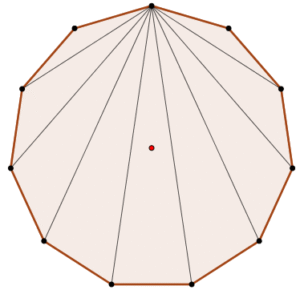 Se puede determinar a través de la siguiente fórmula:
Se puede determinar a través de la siguiente fórmula: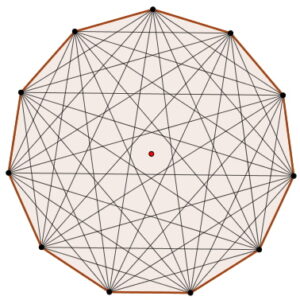 Para calcular el total de diagonales se debe aplicar la siguiente relación:
Para calcular el total de diagonales se debe aplicar la siguiente relación: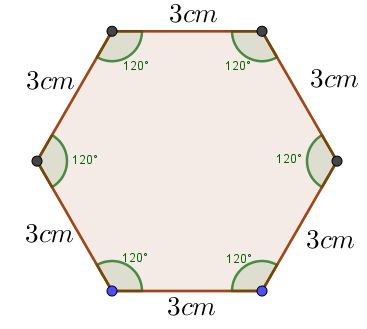
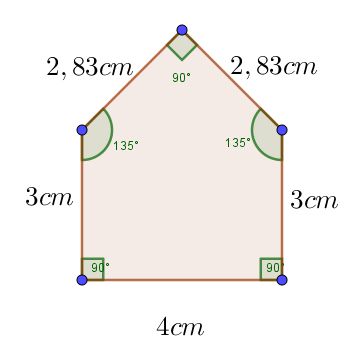





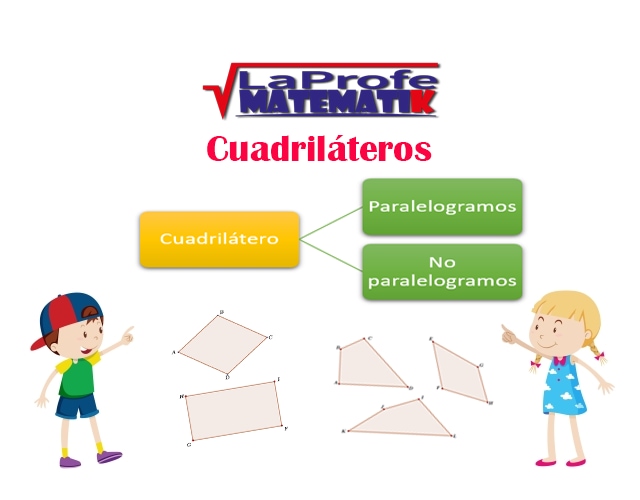
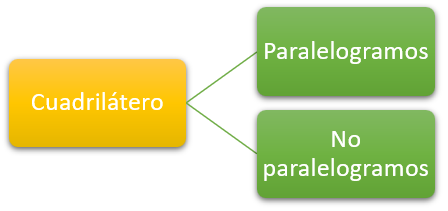
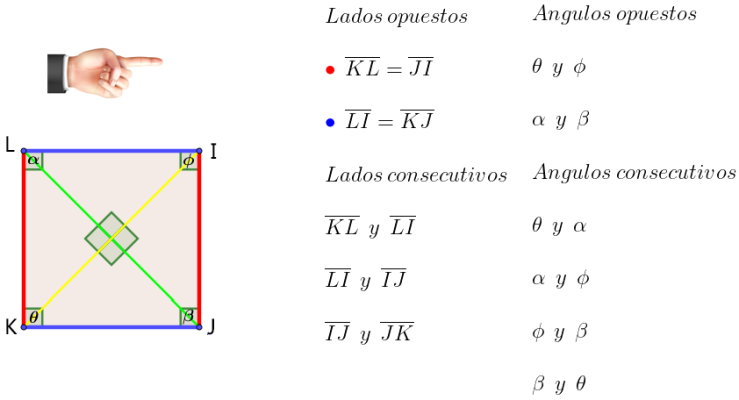
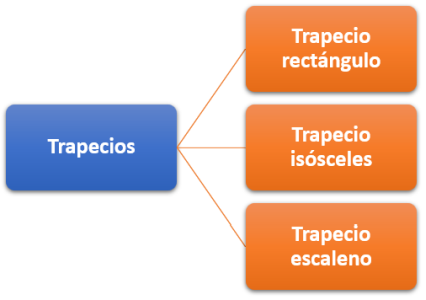
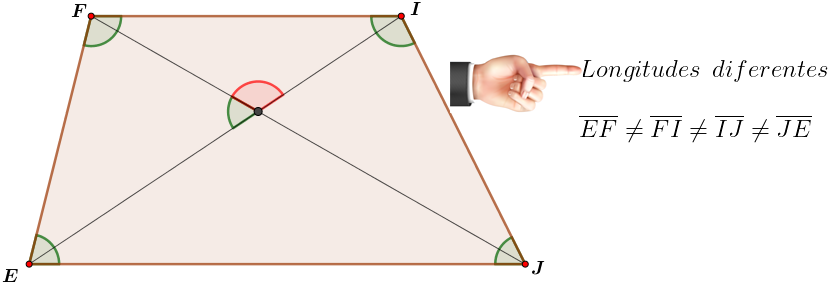
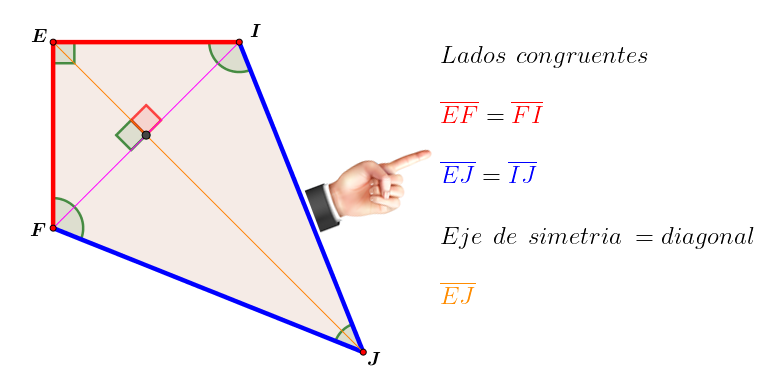
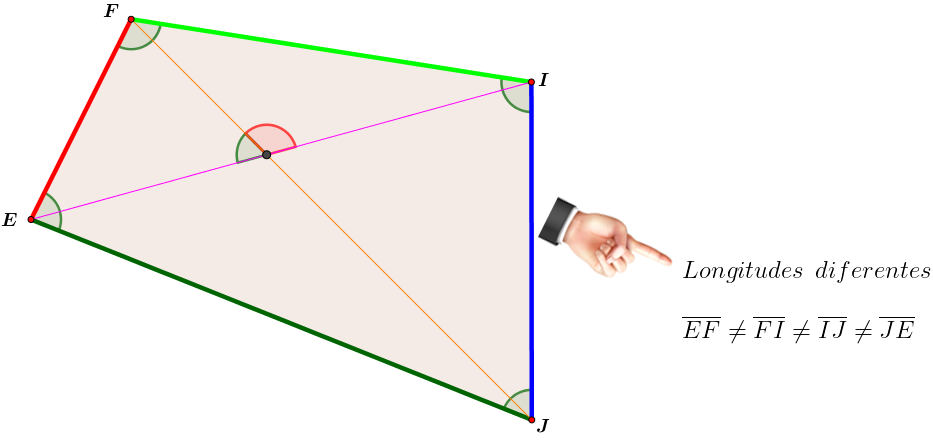
 ¿Te has preguntado alguna vez qué son los cuadriláteros y por qué aparecen tan seguido en tu entorno?
¿Te has preguntado alguna vez qué son los cuadriláteros y por qué aparecen tan seguido en tu entorno?

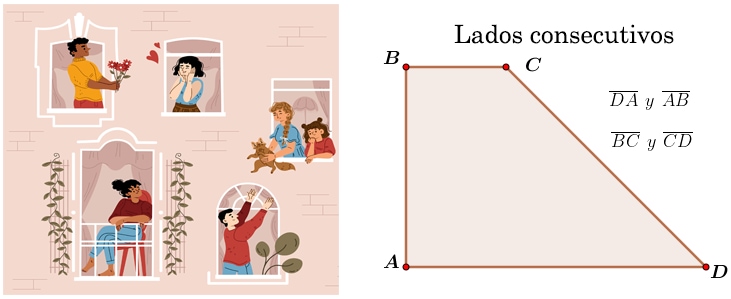
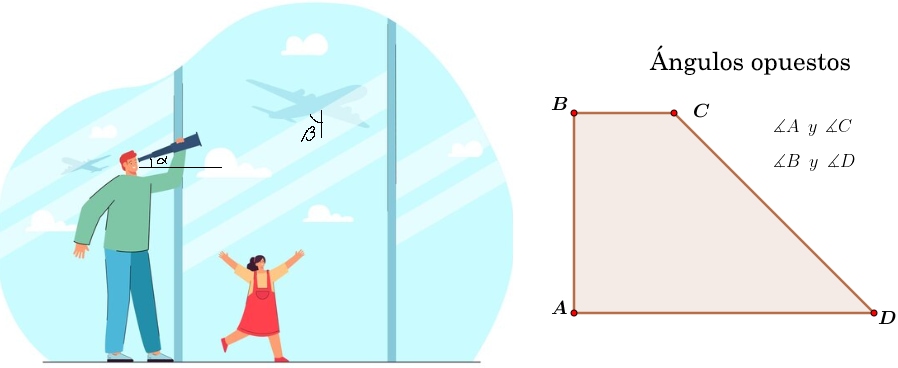
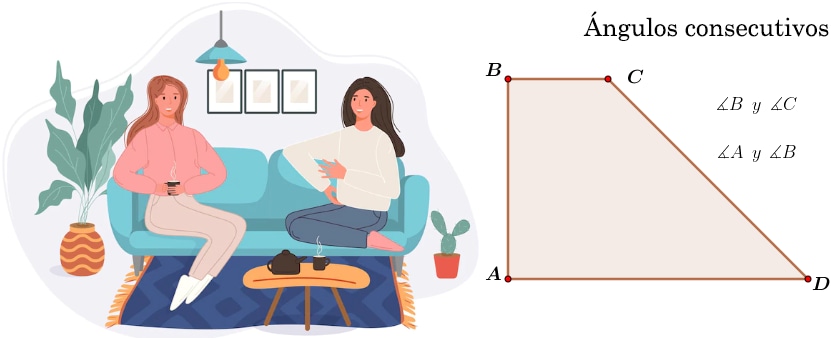







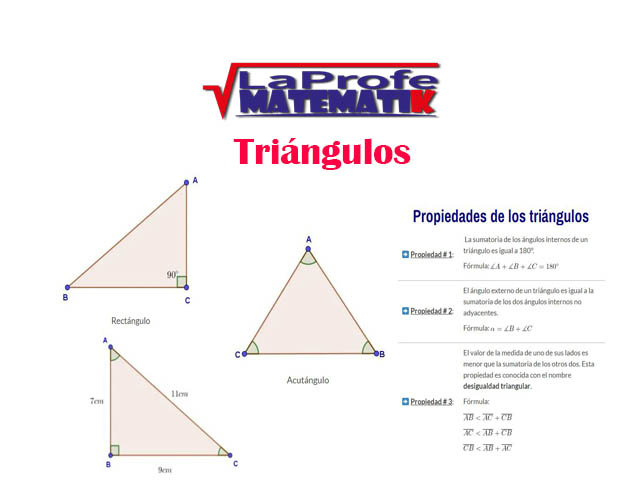
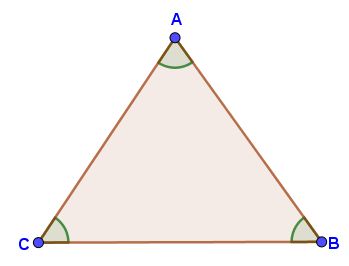
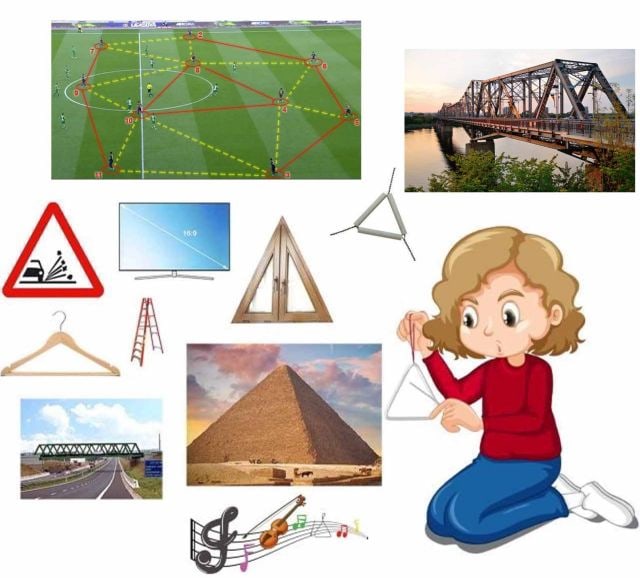 ¿Sabías que los triángulos los puedes ver al tu alrededor? En cualquier lugar donde te encuentres seguramente verás algo que tenga forma triangular, puede ser una ventana, un televisor, un puente, una escalera, las caras de una pirámide, una señal de transito, un velero, un gancho de ropa, entre otros.
¿Sabías que los triángulos los puedes ver al tu alrededor? En cualquier lugar donde te encuentres seguramente verás algo que tenga forma triangular, puede ser una ventana, un televisor, un puente, una escalera, las caras de una pirámide, una señal de transito, un velero, un gancho de ropa, entre otros.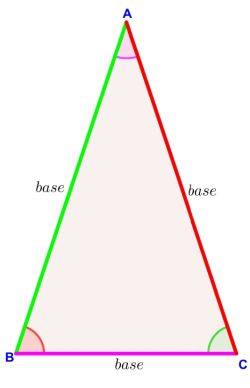
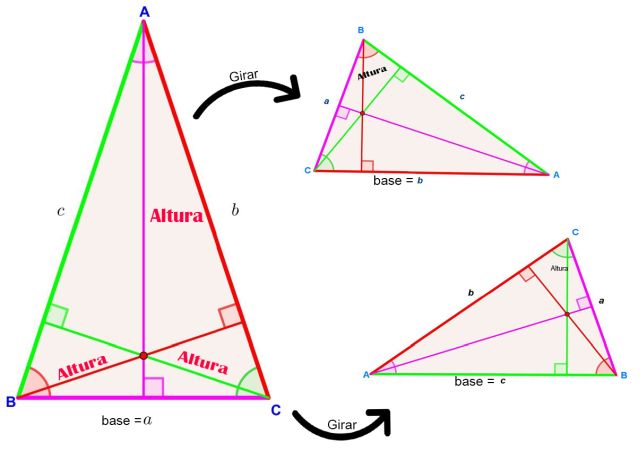
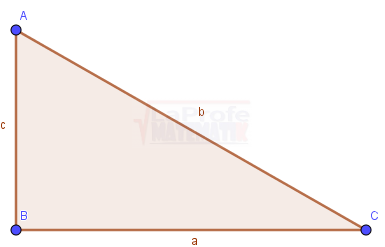
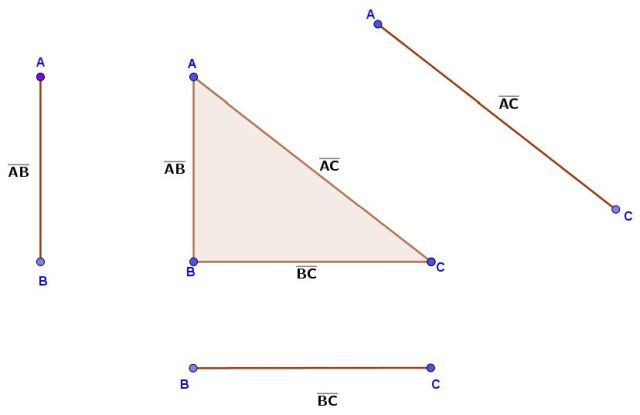

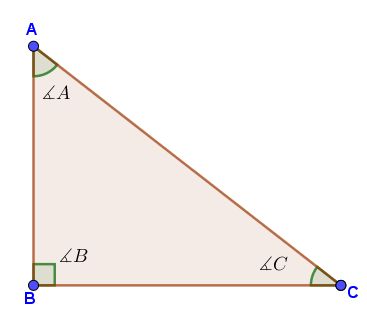

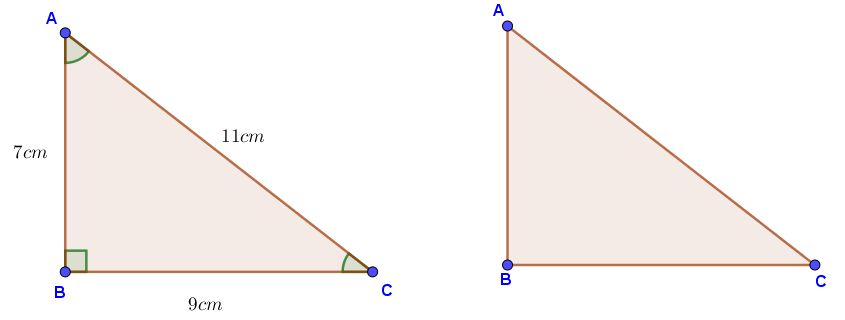


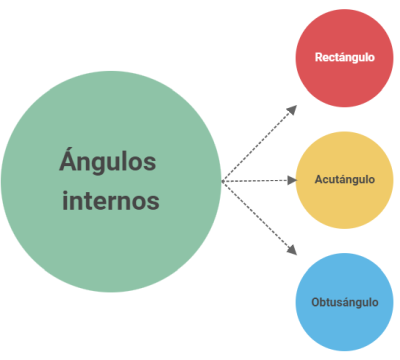
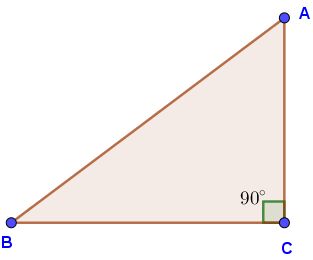
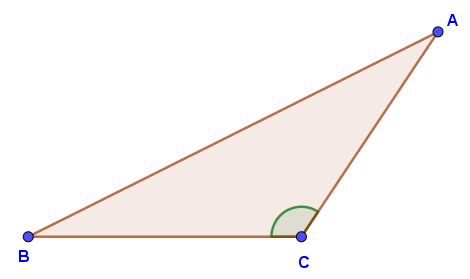
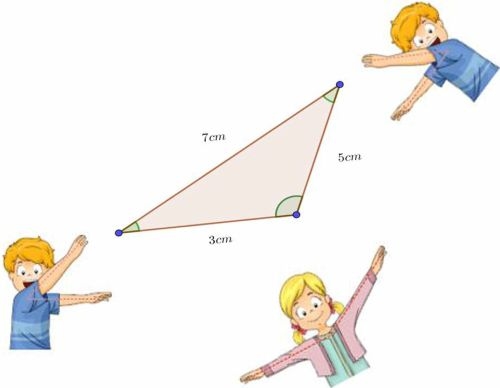
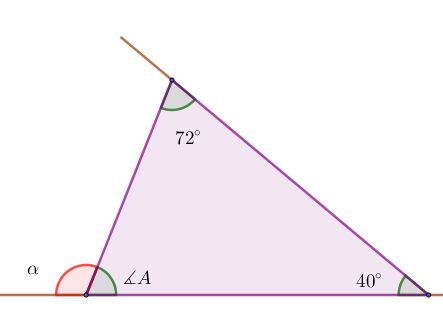

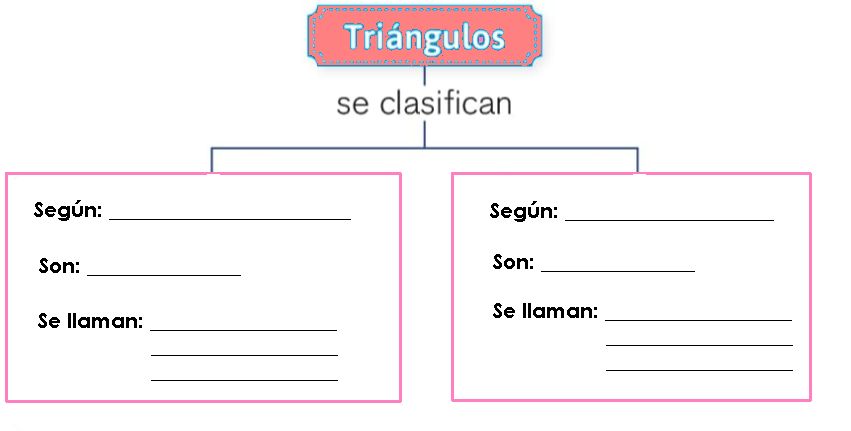
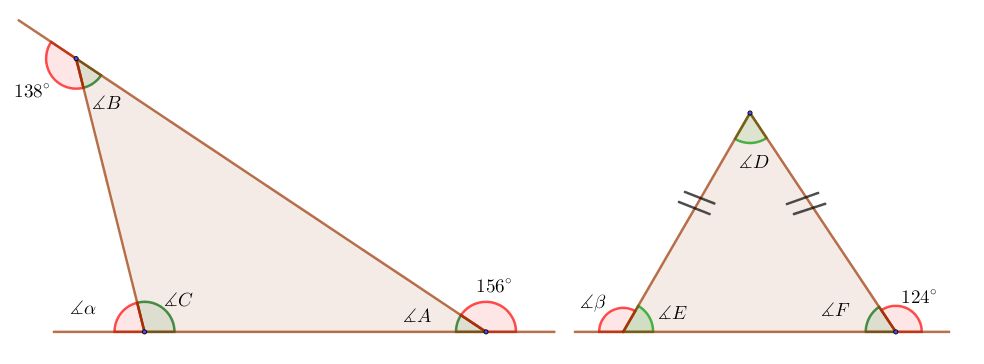 Observa muy detenidamente el triángulo y justifica porque no se puede construir.
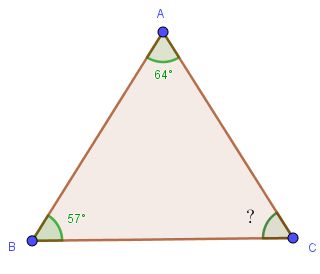
Observa muy detenidamente el triángulo y justifica porque no se puede construir.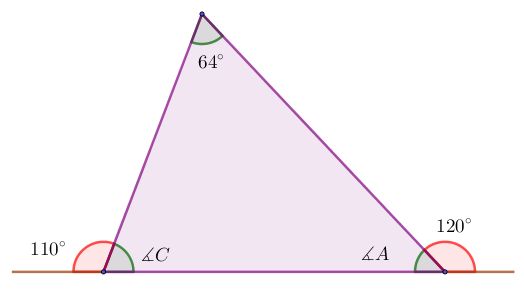 ¿Se pueden dibujar los siguientes triángulos? Aplica la propiedad # 3 y haz triángulos con las siguientes medidas:
¿Se pueden dibujar los siguientes triángulos? Aplica la propiedad # 3 y haz triángulos con las siguientes medidas: 




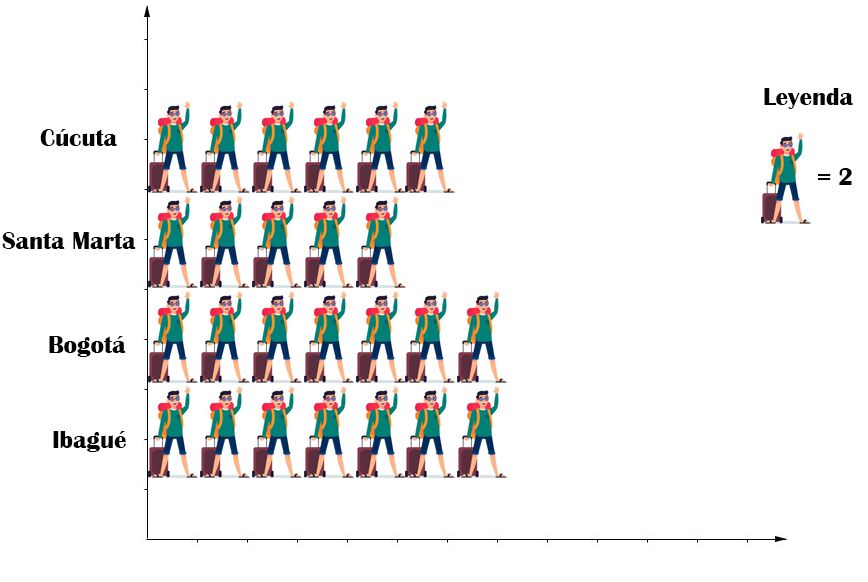




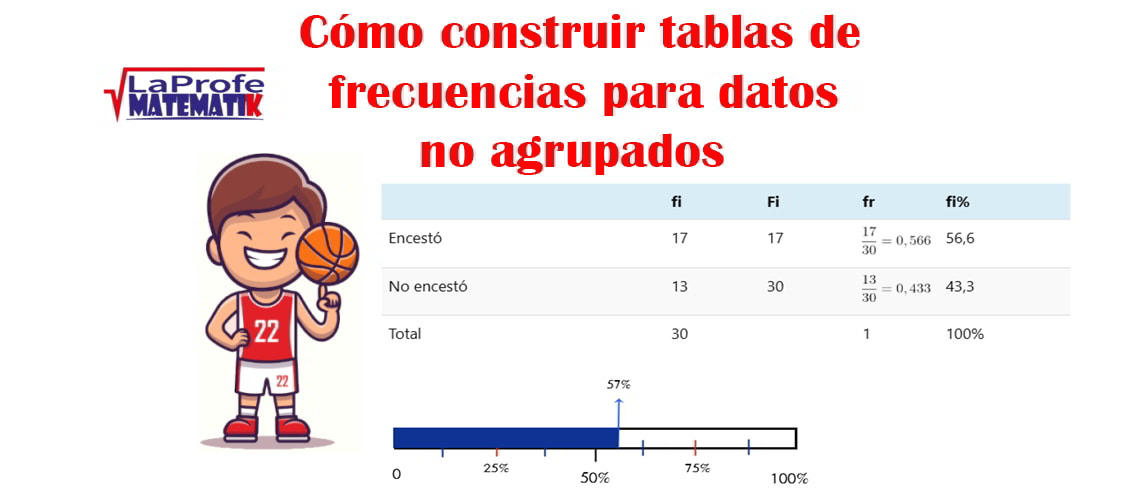
 ¿Te has preguntado alguna vez Cómo construir tablas de frecuencias y por qué esa habilidad te hace la vida más fácil? Aprender a ordenar datos —desde las calificaciones de un salón hasta cuántas horas pasas en redes cada día— te permite ver patrones, tomar decisiones rápidas y explicar resultados con claridad.
¿Te has preguntado alguna vez Cómo construir tablas de frecuencias y por qué esa habilidad te hace la vida más fácil? Aprender a ordenar datos —desde las calificaciones de un salón hasta cuántas horas pasas en redes cada día— te permite ver patrones, tomar decisiones rápidas y explicar resultados con claridad. Alfonso realizó 30 lanzamientos de balón de baloncesto, intentando encestar cada vez en menos de tres segundos. Los resultados obtenidos fueron los siguientes:
Alfonso realizó 30 lanzamientos de balón de baloncesto, intentando encestar cada vez en menos de tres segundos. Los resultados obtenidos fueron los siguientes: