¿Sabes cómo determinar el rango de una función? Antes de la explicación de este tema, es necesario conocer su definición, también conocido con el nombre de recorrido, el cual se define como el conjunto de las imágenes de la función, el rango es el segundo valor de cada par ordenado, es decir, que gráficamente está localizado en el eje de las ordenadas o eje “y”. Se simboliza como Rgo f
Rango de una función gráficamente
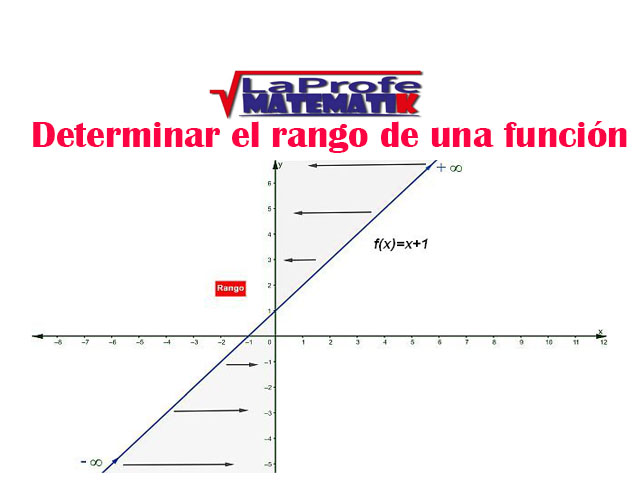
A continuación, observa la siguiente imagen donde está graficada la función $$f(x)=x+1$$
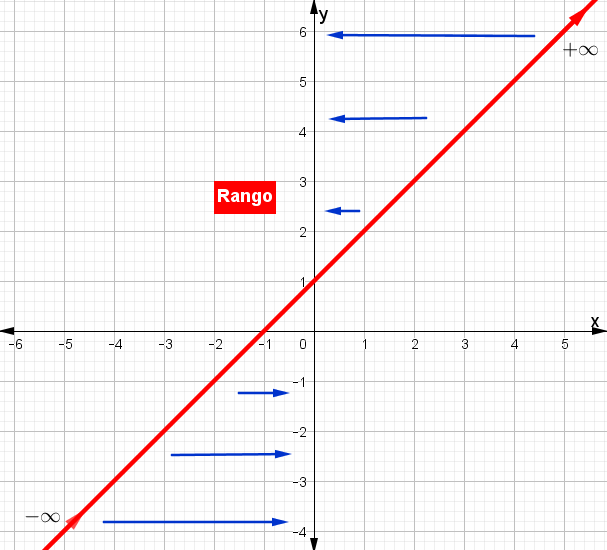
Para poder representar gráficamente la recta de la fig#1, en primer lugar se sustituyen los valores arbitrarios de “x” en la función \(f(x)=x+1\) , estos valores son pertenecientes al dominio o al conjunto de partida, luego se obtiene las imágenes o rango es decir los valores de “y”.
El rango de toda función es la proyección de la recta o la curva graficada sobre el eje “y”, el rango de la función \(f(x)=x+1\) proviene del – ∞ hacia el + ∞ esto quiere decir que el rango de esta función son todos los ℜ.
Métodos para determinar el rango
Para determinar el rango de una función, que es el conjunto de todos los valores de salida o valores de “y” posibles, se puede utilizar métodos analíticos y gráficos.
Método analítico
Se enfoca en la expresión matemática de la función. Existe dos enfoques principales: trata de despejar la variable “x” y determinar si existen o no restricciones en “y”
Despejando la variable “x”
El rango de la función y = f ( x ) es el dominio de su función inversa, x = f -1( y ) . Para determinar el rango debes cumplir con los siguientes pasos:
- Reemplaza f ( x ) con y.
- Despejar la variable x en términos de y.
- Determina el dominio de la nueva función, que ahora está en términos de y. Este dominio es el rango de la función original.
Ejemplo:
Determina el rango de la siguiente función
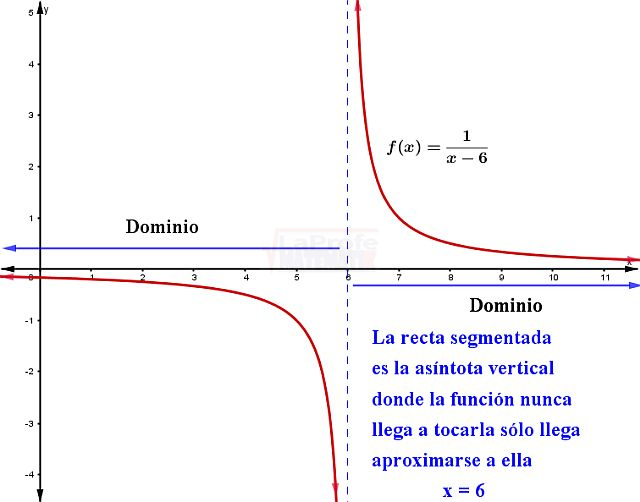
$$f(x)=\frac{1}{x-4}$$
Solución:
$$y=\frac{1}{x-4}$$
$$y(x-4)=1\Rightarrow yx-4y=1\Rightarrow$$
$$yx=1+4y\Rightarrow $$
$$x=\frac{1+4y}{y}$$
Al observar la nueva función, la variable y no puede ser cero. Por lo tanto, el dominio de esta nueva función son todos los \(\mathbb{R}\) a excepción del cero.
El rango de la función original es:
$$R_{f}=\left ( -\infty ,0 \right )\cup \left ( 0,\infty \right )$$
Analizando la función
Esta modalidad es útil para funciones más simples como las cuadráticas, exponenciales y la trigonométricas.
Funciones cuadráticas
Para este tipo de funciones el rango depende del vértice, si:
- a > 0, la parábola es cóncava hacia arriba dónde el vértice es el valor mínimo y el rango es [ yvértice , ∞ ).
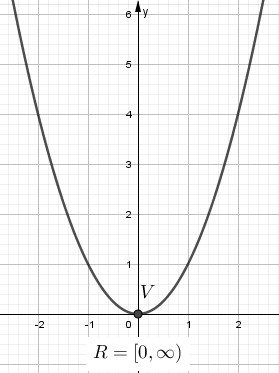
- a < 0, la parábola es cóncava hacia abajo dónde el vértice es el valor mínimo y el rango es [ yvértice , ∞ ).
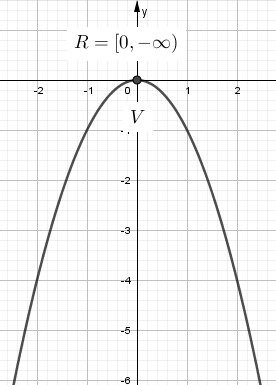
Para determinar la coordenada “ y ” del vértice es a través de la siguiente expresión:
$$y_{vertice}=f\left ( -\frac{b}{2a} \right )$$
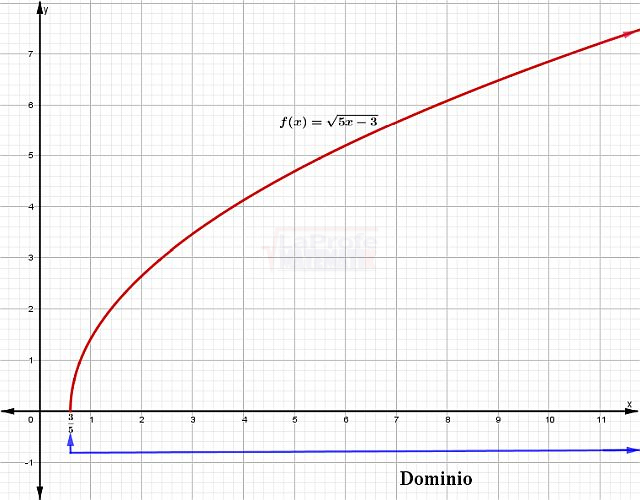
Funciones con raíces de índice par
Para funciones como \(f(x)=\sqrt{x-3}\), la cantidad subradical debe ser positiva, es decir, \(x-3\geq 0\). Por lo tanto, el rango es [ 0, ∞ ).
Método gráfico
Es un método visual y a menudo más intuitivo. Para determinar el rango, sólo debes proyectar verticalmente la gráfica en el eje “ y ”.
Ejemplos
Analice las funciones representadas en las siguientes gráficas, posteriormente determine dominio y rango.
Dada la función:
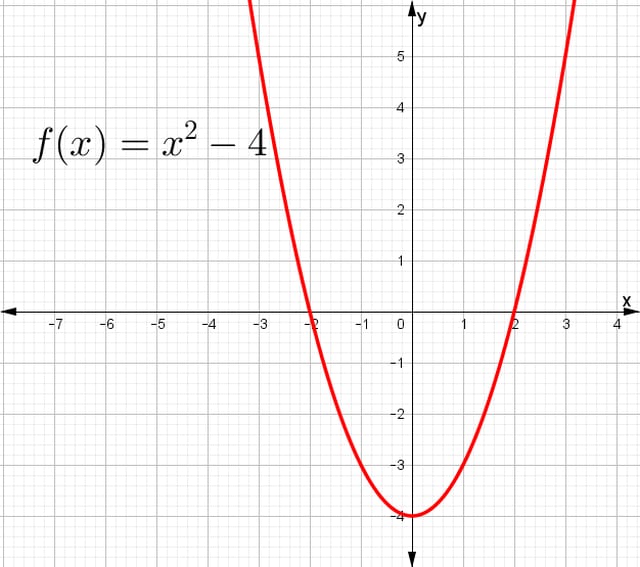
$$f(x)=x^{2}-4$$
En el eje “x” está definida para todos los valores, es decir que el dominio es: $$D_{f}=\mathbb{R}$$
En el eje “y” está definida para valores mayores o iguales a: -4, es decir que el rango es:
$$R_{f}=[-4,\infty )$$
Gráfica
Dada la función:
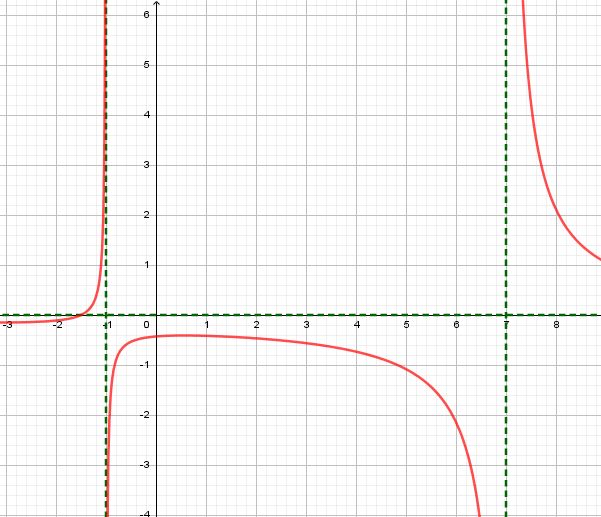
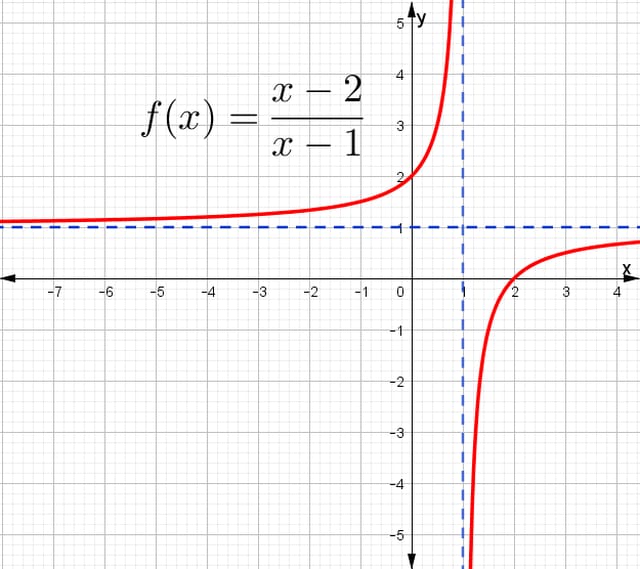
$$f(x)=\frac{x-2}{x-1}$$
En el eje “x” No está definida para x = 1, es decir que el dominio es :
$$D_{f}=(-\infty , 1)\cup (1,\infty )$$
En el eje “y” El 1 No es imagen de ningún elemento de x, es decir que el rango es:
$$R_{f}=(-\infty , 1)\cup (1,\infty )$$
Gráfica
Ejercicio resuelto
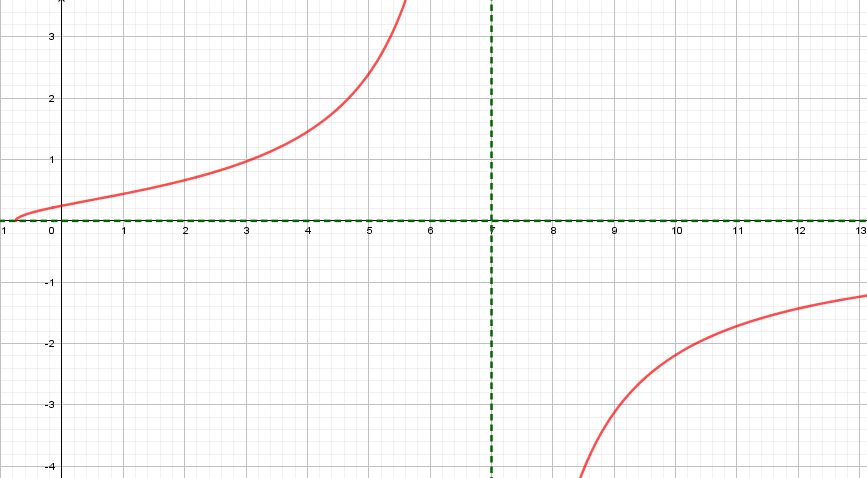
Grafique y determine el dominio y rango de la siguiente función:
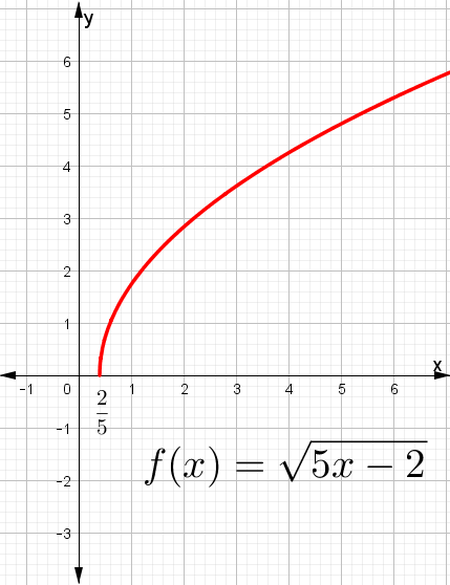
$$f(x)=\sqrt{5x-2}$$
Solución:
Como es una función radical de índice par la cantidad subradical debe ser positiva, entonces, los valores de “x ”deben ser:
$$\sqrt{5x-2}\geq 0$$
$$5x-2\geq 0$$
$$5x\geq 2$$
$$x\geq \frac{2}{5}$$
Por lo tanto el dominio de la función es:
$$D_{f}=\left [ \frac{2}{5},\infty \right )$$
Cálculo del rango
$$f(x)=\sqrt{5x-2}$$
$$y=\sqrt{5x-2}$$
$$y^{2}=5x-2$$
$$x=\frac{y^{2}+2}{5}$$
La nueva función no tiene restricciones para los valores de y. Pero la función original, \(f(x)=\sqrt{5x-2}\) es una raíz cuadrada de un número real que nunca puede ser negativo. Por lo tanto, el valor de y siempre debe ser ≥ 0.
Combinando la restricción de la función original y el resultado del despeje, el rango de la función es:
$$R_{f}=[ 0,\infty )$$
Todos los valores posibles de salida es cualquier número real no negativo.
Tabla de valores
| x | f ( x ) |
| 2/5 | 0 |
| 1 | $$\sqrt{3}$$ |
| 2 | $$2\sqrt{2}$$ |
| 3 | $$\sqrt{13}$$ |
| 4 | $$3\sqrt{2}$$ |
| 5 | $$\sqrt{23}$$ |
| 6 | $$2\sqrt{27}$$ |
El dominio inicia desde 2/5 es decir 0,4. Por lo tanto se crea la tabla de valores a partir de ese valor mínimo.
Gráfica
Actividades
Hacer el estudio de cada una de las siguientes funciones determinando:
- Dominio
- Rango
- Gráfico
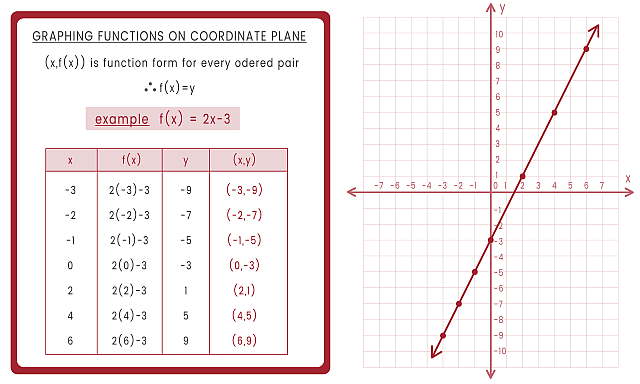
| 1 | $$f(x)=2x-3$$ |
| 2 | $$f(x)=x^{2}+4$$ |
| 3 | $$f(x)=\sqrt{x+5}$$ |
| 4 | $$f(x)=\frac{3}{x-2}$$ |
| 5 | $$f(x)=|x|-1$$ |
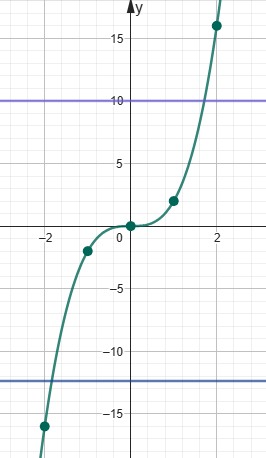
| 6 | $$f(x)=\left ( x+1 \right )^{3}$$ |
| 7 | $$f(x)=\frac{1}{\sqrt{x}}$$ |
| 8 | $$f(x)=\sqrt{9-x^{2}}$$ |
| 9 | $$f(x)=\left | x\right |$$ |
| 10 | $$f(x)=e^{x}$$ |
Resultados
| 1 | $$D_{f}=(-\infty ,\infty )$$ $$R_{f}=( -\infty ,\infty )$$ |
| 2 | $$D_{f}=(-\infty ,\infty )$$ $$R_{f}=[ 4 ,\infty )$$ |
| 3 | $$D_{f}=[-5,\infty )$$ $$R_{f}=[ 0 ,\infty )$$ |
| 4 | $$D_{f}=(-\infty ,2 )\cup(2,\infty )$$ $$R_{f}=( -\infty ,0 )\cup (0,\infty )$$ |
| 5 | $$D_{f}=(-\infty ,\infty )$$ $$R_{f}=[ -1 ,\infty )$$ |
| 6 | $$D_{f}=(-\infty ,\infty )$$ $$R_{f}=( -\infty ,\infty )$$ |
| 7 | $$D_{f}=(0 ,\infty )$$ $$R_{f}=( 0 ,\infty )$$ |
| 8 | $$D_{f}=\left [ -3,3 \right ]$$ $$R_{f}=\left [ 0,3 \right ]$$ |
| 9 | $$D_{f}=(-\infty , \infty )$$ $$R_{f}=\left [ 0,\infty \right )$$ |
| 10 | $$D_{f}=(-\infty , \infty )$$ $$R_{f}=\left ( 0,\infty \right )$$ |

 ¿Sabías que las funciones están presentes en muchos aspectos de nuestra vida diaria? Aunque no siempre nos demos cuenta, constantemente utilizamos relaciones que pueden expresarse como funciones.
¿Sabías que las funciones están presentes en muchos aspectos de nuestra vida diaria? Aunque no siempre nos demos cuenta, constantemente utilizamos relaciones que pueden expresarse como funciones.



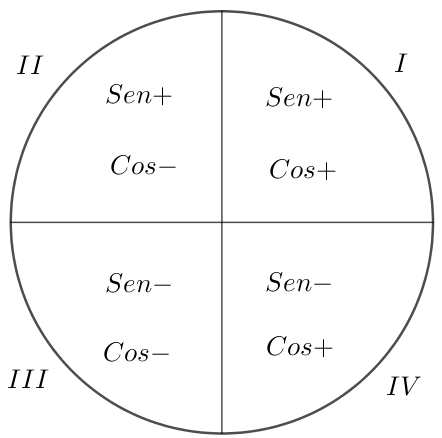










 ¿Sabías que los ángulos coterminales están presente en muchos objetos y situaciones que ves a diario? Desde el giro de las manecillas de un reloj hasta los movimientos en tu videojuego favorito, los ángulos coterminales están por todas partes. Comprender qué es un ángulo coterminal te permitirá reconocer patrones de rotación, medir desplazamientos y entender mejor el mundo que te rodea.
¿Sabías que los ángulos coterminales están presente en muchos objetos y situaciones que ves a diario? Desde el giro de las manecillas de un reloj hasta los movimientos en tu videojuego favorito, los ángulos coterminales están por todas partes. Comprender qué es un ángulo coterminal te permitirá reconocer patrones de rotación, medir desplazamientos y entender mejor el mundo que te rodea.