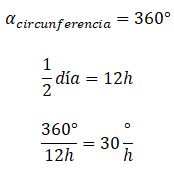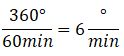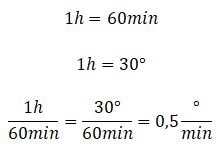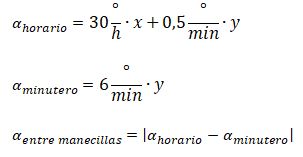¿Sabías que las medidas de posición no central son esenciales para interpretar cómo se distribuyen los datos en una población?
¿Sabías que las medidas de posición no central son esenciales para interpretar cómo se distribuyen los datos en una población?
Cuando analizas calificaciones, tiempos deportivos o resultados de encuestas, no basta con conocer el promedio; también importa en qué lugar se encuentra un valor respecto a los demás.
Las medidas de posición no central, como los cuartiles, deciles y percentiles, nos permiten identificar esa posición relativa, ayudándonos a entender si un resultado está entre los más bajos, promedio o destacados.
En esta guía aprenderás qué son, cómo calcularlas paso a paso para datos agrupados y cómo interpretarlas correctamente en situaciones reales.
Medidas de localización
Concepto
Las medidas de localización, también conocidas como medidas de posición, son herramientas estadísticas que permiten comprender y describir dónde se sitúan las observaciones dentro de un conjunto de datos.
Clasificación
Las medidas de localización como se sabe son estadísticos que indican la posición de los datos dentro de una distribución.
Su finalidad es ubicar valores representativos o puntos de referencia que describen cómo se distribuyen los datos.
Se clasifican en dos grandes grupos: Medidas de tendencia central y medidas de posición no central.
Medidas de Tendencia Central
Las medidas de posición central dividen el conjunto de datos en dos partes iguales, e indican el valor que representa el centro o punto medio de un conjunto de datos.
Su intención es resumir el conjunto con un solo valor representativo, mostrando hacia dónde tienden los datos.
Medidas de posición no central
Son utilizados para determinar qué tan alto o bajo está un valor respecto al total dividiendo al conjunto de datos en más de dos partes iguales.
Medidas de Posición No Central
También son llamados Cuantiles, estas medidas como ya se sabe tienen la función de dividir un conjunto de datos en más de dos partes iguales. Para ello, es indispensable que las observaciones se encuentren ordenadas de forma ascendente. Su utilidad radica en que permiten identificar la distribución de los datos en diferentes segmentos, ofreciendo una visión más detallada de su comportamiento.
Clasificación
Las medidas de posición no central se clasifican en:
- Cuartiles,
- Deciles y
- Percentiles.
Cuartiles (Q)
Son tres valores (Q1, Q2 y Q3) que dividen un conjunto de datos ordenados en cuatro partes iguales.
Esto genera cuatro segmentos de datos, cada uno con una proporción similar de elementos, lo cual permite identificar la distribución de los datos en diferentes rangos.
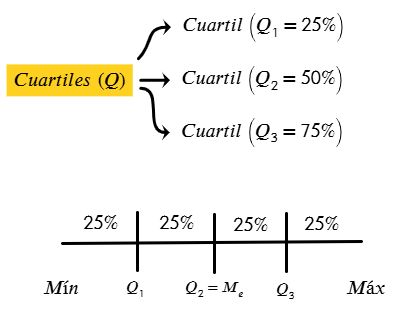
Q1 (Primer Cuartil): Es el valor por debajo del cual se encuentra el 25% de los datos.
Q2 (Segundo Cuartil): Valor por debajo del cual se encuentra el 50% de los datos. El Cuartil 2 siempre coincide con la mediana (Q2 = Me)
Q3 (Tercer Cuartil): Representa el valor por debajo del cual se encuentra el 75% de los datos.
Fórmula
Para calcular los cuartiles cuando se dispone de una tabla de distribución de frecuencias con datos agrupados en intervalos, es necesario determinar primero su posición utilizando la siguiente expresión:
$$P=\frac{n\cdot k}{4}$$
Y finalmente se calcula el Cuartil Qk para datos agrupados:
$$Q_{k}=L_{i}+\frac{\frac{n\cdot k}{4}-F_{i-1}}{f_{i}}\cdot a$$
Donde:
k = Cuartil que se desea hallar, su valor es 1, 2 o 3.
LI = Límite inferior del intervalo representativo.
fI = Frecuencia absoluta del intervalo.
FI-1 = Frecuencia absoluta acumulada anterior a la frecuencia absoluta acumulada al intervalo representativo.
a = Amplitud de cada intervalo.
Deciles (D)
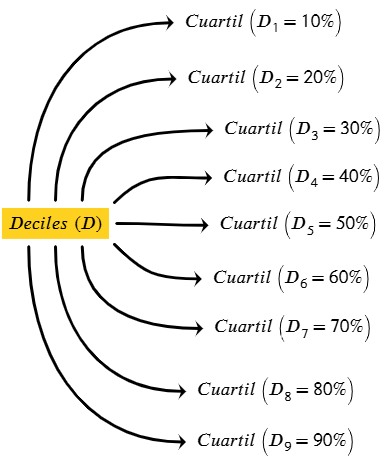
Son nueve valores (D1, D2,…,D9) que dividen un conjunto de datos ordenados en forma ascendente en diez partes iguales.
Esta situación crea 10 segmentos de datos, cada uno conteniendo una proporción similar de elementos, permitiendo una identificación más granular de la distribución de los datos.
D1 (Primer Decil): Es el valor por debajo del cual se encuentra el 10% de los datos.
D2 (Segundo Decil): Es el Valor por debajo del cual se encuentra el 20% de los datos. El Cuartil 2 siempre coincide con la mediana (D2 = Me)
D9 (Noveno Decil): Constituye el valor por debajo del cual se encuentra el 90% de los datos.
Fórmula
Para determinar el Decil Dk para datos agrupados, debes aplicar la siguiente expresión:
$$D_{k}=L_{i}+\frac{\frac{n\cdot k}{10}-F_{i-1}}{f_{i}}\cdot a$$
Donde:
k = Decil que necesitas encontrar, su valor es 1, 2, 3, 4, 5, 6, 7, 8 y 9.
Percentiles (P)
Son noventa y nueve valores (P1, P2, P3, P4, P5,…, P99) que tienen como finalidad dividir el conjunto de datos en cien partes iguales.
Cada una de estas partes contiene aproximadamente el mismo porcentaje de observaciones, proporcionando una visión extremadamente detallada de la distribución de los datos.
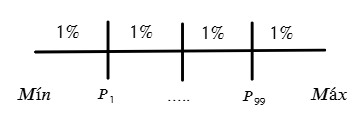
P1 (Primer Percentil): Define el valor por debajo del cual se encuentra el 1% de los datos.
P10 (Décimo Percentil): Indica el valor por debajo del cual se encuentra el 10% de los datos (El Percentil 10 coincide con el Decil 1 (P10 = D1)
P25 (Vigésimo quinto Percentil): Es el valor que marca el límite inferior para el 25% de los datos (concuerda con el Primer Cuartil, Q1) .
P50 (Quincuagésimo Percentil): Es el valor central, por debajo del cual se encuentra el 50% de los datos. Este percentil coincide con la mediana, el segundo Cuartil (Q2) y el quinto Decil (D5).
P75 (Septuagésimo Quinto Percentil): Representa el valor por debajo del cual se encuentra el 75% de los datos (coincide con el Tercer Cuartil, Q3).
P99 (Nonagésimo Noveno Percentil): Es el valor por debajo del cual se encuentra el 99% de los datos.
Fórmula
La fórmula para calcular el percentil Pk es la siguiente:
$$P_{k}=L_{i}+\frac{\frac{n\cdot k}{100}-F_{i-1}}{f_{i}}\cdot a$$
Ejemplo realizado paso a paso
Una empresa de telecomunicaciones está analizando el tiempo (en minutos) que sus empleados tardan en responder a los correos electrónicos de clientes, con el objetivo de optimizar la eficiencia. Se han recolectado datos de 100 empleados durante una semana y se han agrupado en intervalos de tiempo. Determinar el Percentil 73, Cuartil 3 y el Decil 2.
Tiempo en responder correos electrónicos
Tiempo de respuesta (min) [Li – Ls) | Marca de clase xi | Frecuencia absoluta fi | Frecuencia absoluta acumulada Fi | ||
| 1 | 0 | 10 | 5 | 15 | 15 |
| 2 | 10 | 20 | 15 | 25 | 40 |
| 3 | 20 | 30 | 25 | 35 | 75 |
| 4 | 30 | 40 | 35 | 18 | 93 |
| 5 | 40 | 50 | 45 | 7 | 100 |
| n= | 100 | ||||
Solución
n = 100 (Total de datos)
a = 10 (Amplitud del intervalo de clase)
Cálculo de los Cuantiles
A continuación, el cálculo del Percentil 73, Cuartil 3 y Decil 2.
Percentil (P73) y su interpretación
Cálculo de la posición:
$$P=\frac{100\cdot 73}{100}=73$$
En la columna de frecuencia absoluta acumulada se ubica el valor ≥ 73, de esta forma se puede determinar el intervalo del Percentil 73 que es = [20 – 30).
Calculo del P73 :
$$P_{73}=20+\frac{73-40}{35}\cdot 10$$
$$P_{73}=20+\frac{33}{35}\cdot 10$$
$$P_{73}=20+0,9428\cdot 10$$
$$P_{73}=20+9,428$$
$$P_{73}=29,428\,minutos$$
Interpretación: El 73% de los empleados tarda 29,428 minutos o menos en responder a los correos de los clientes.
Cuartil 3 (Q3) e interpretación
Posición:
$$P=\frac{100\cdot 3}{4}=75$$
Con el valor de la posición se busca en la columna de frecuencia absoluta acumulada el valor ≥ 75. Por lo tanto, el intervalo del Cuartil 3 es = [20 – 30).
Q3 :
$$Q_{3}=20+\frac{75-40}{35}\cdot 10$$
$$Q_{3}=20+\frac{35}{35}\cdot 10$$
$$Q_{3}=20+1\cdot 10$$
$$Q_{3}=20+10$$
$$Q_{3}=30\,minutos$$
Interpretación: El 75% de los empleados tarda 30 minutos o menos en responder a los correos. Esto significa que el 25% de los empleados más rápidos (Q1) tarda 30 minutos o menos, y el 25% restante tarda más de 30 minutos (ubicados entre el valor de Q3 y el valor máximo)
Cálculo e interpretación del Decil 2 (D2)
Posición:
$$P=\frac{100\cdot 2}{10}=20$$
Según la posición (P=20), el intervalo del Decil 2 es = [10, 20)
D2:
$$D_{2}=10+\frac{20-15}{25}\cdot 10$$
$$D_{2}=10+\frac{5}{25}\cdot 10$$
$$D_{2}=10+0,2\cdot 10$$
$$D_{2}=10+2$$
$$D_{2}=12\,minutos$$
Interpretación: El 20% de los empleados tarda 12 minutos o menos en responder a los correos, es decir, son este 20% es grupo.
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
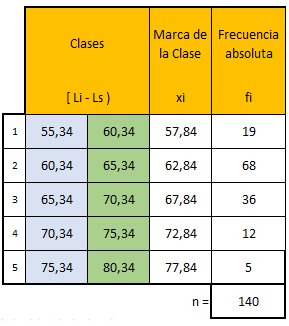
Parte I: Completa la tabla de distribución de frecuencias y calcule los cuantiles a continuación:
- Percentil 5, 36, 78, 96
- Cuartiles 1, 2.
- Deciles 3, 9
Parte II. Lea atentamente y seleccione la opción correcta:
1.¿Cuál de las siguientes medidas de localización es la más sensible a los valores atípicos (outliers) en un conjunto de datos?
- Mediana
- Moda
- Cuartil 1
- Media Aritmética
- Percentil 50
2.Si en un conjunto de datos el segundo cuartil (Q2) es igual al percentil 50 P50 y también al decil 5 (D5), ¿a qué otra medida de tendencia central fundamental coincide siempre?
- Moda
- Media Aritmética
- Rango
- Mediana
- Desviación Estándar
3.Una empresa de juguetes registra las edades de los niños a los que van dirigidos sus productos. Si el Decil 7 (D7) de las edades es 8 años, ¿qué significa esto?
- El 7% de los niños tiene 8 años o menos.
- El 70% de los niños tiene 8 años o más.
- El 30% de los niños tiene 8 años o menos.
- El 70% de los niños tiene 8 años o menos.
- El 8% de los niños tiene 7 años o menos.
4.Para calcular un cuantil (como un cuartil o percentil) en una tabla de distribución de frecuencias de datos agrupados, ¿cuál es el primer paso indispensable antes de aplicar la fórmula?
- Calcular la media aritmética de los datos.
- Determinar la desviación estándar del conjunto.
- Ordenar los datos de forma descendente.
- Hallar la posición del cuantil deseado.
- Identificar la moda de la distribución.
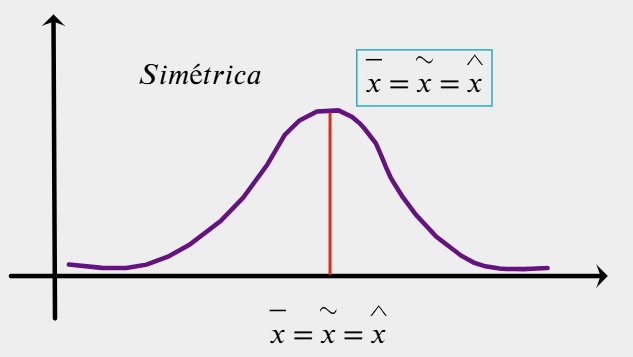
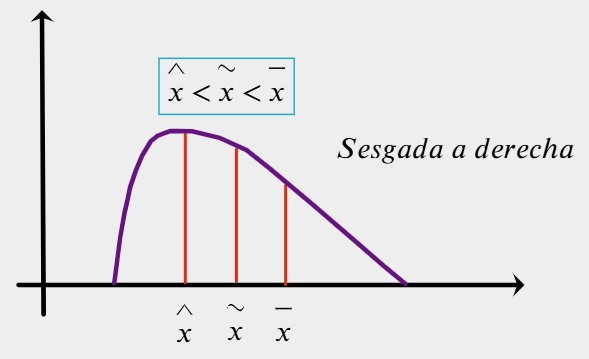
5.En una distribución de datos perfectamente simétrica y unimodal (como la distribución normal), ¿qué relación se cumple entre sus medidas de tendencia central?
- Moda < Mediana < Media
- Media < Mediana < Moda
- Moda = Mediana = Media
- Mediana = 0 y Media = 0
- Solo la Media y la Mediana son iguales, la Moda es diferente.
Parte III. Contesta Verdadero o Falso las siguientes afirmaciones:
1.Las medidas de localización solo incluyen la media, la mediana y la moda.
- Verdadero.
- Falso.
2.Si el Cuartil 2 (Q2) de un conjunto de datos es 15, significa que el 25% de los datos es igual o menor a 15.
- Verdadero.
- Falso.
3.En una distribución de datos simétrica, la media, la mediana y la moda siempre coinciden en el mismo valor.
- Verdadero.
- Falso.
4.Un «outlier» (valor atípico) es un punto de dato que se desvía significativamente del resto de los datos en un conjunto.
- Verdadero.
- Falso.
5.El Decil 9 (D9) indica el valor por debajo del cual se encuentra el 99% de los datos.
- Verdadero.
- Falso.
Parte IV: Ordena la Lógica
Desafía tu comprensión del tema. Lee cuidadosamente las siguientes afirmaciones relacionadas con el cálculo y la interpretación de cuantiles. Luego, ordénalas en la secuencia lógica correcta para describir el proceso general de cómo se utilizan estas medidas.
Elementos a Ordenar:
- Se interpretan los resultados para entender la posición relativa de los datos, como identificar el 25% más bajo o el 75% más alto.
- Se aplica una fórmula específica (como la de interpolación para datos agrupados) para obtener el valor numérico del cuantil deseado.
- Se seleccionan los cuantiles específicos (cuartiles, deciles o percentiles) que son relevantes para la pregunta de investigación.
- Se identifican los datos y se organizan de forma ascendente, ya sea individualmente o en una tabla de distribución de frecuencias.
- Se calcula la posición teórica del cuantil dentro del conjunto de datos ordenado.
Respuestas de las partes
II (1D; 2D; 3D; 4D; 5C)
III (1B; 2B; 3A; 4A; 5B)
IV (4, 3, 5, 2, 1)
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión



 ¿Sabes qué tienen en común la media aritmética, la mediana y la moda con tus redes sociales favoritas o tus videojuegos?
¿Sabes qué tienen en común la media aritmética, la mediana y la moda con tus redes sociales favoritas o tus videojuegos?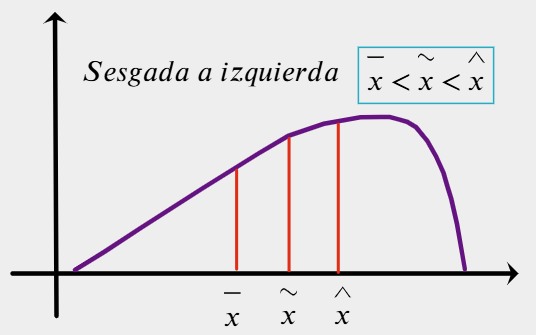

 ¿Alguna vez te has preguntado cómo las medidas de dispersión revelan lo que las cifras promedio esconden? Piensa en tu videojuego favorito: tu puntaje medio es de 5000 puntos por partida, pero eso no dice si juegas siempre igual o si un día haces 1000 y al siguiente rompes récords con 9000.
¿Alguna vez te has preguntado cómo las medidas de dispersión revelan lo que las cifras promedio esconden? Piensa en tu videojuego favorito: tu puntaje medio es de 5000 puntos por partida, pero eso no dice si juegas siempre igual o si un día haces 1000 y al siguiente rompes récords con 9000. Antes de profundizar en el tema, es fundamental dominar ciertos conceptos. A continuación, se detallan las terminologías esenciales:
Antes de profundizar en el tema, es fundamental dominar ciertos conceptos. A continuación, se detallan las terminologías esenciales: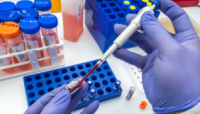 Es una parte representativa seleccionada de una población. Es aplicado cuando es inviable la recopilación de datos en cada elemento de la población, ya sea por costos, consumo de mucho tiempo, situaciones imposibles en la práctica como contactar a todos los niños de 7 años de un país.
Es una parte representativa seleccionada de una población. Es aplicado cuando es inviable la recopilación de datos en cada elemento de la población, ya sea por costos, consumo de mucho tiempo, situaciones imposibles en la práctica como contactar a todos los niños de 7 años de un país. Ejemplo. Determinar la Desviación Media Absoluta
Ejemplo. Determinar la Desviación Media Absoluta Ejemplo. Calcular la varianza
Ejemplo. Calcular la varianza
 Ejemplo
Ejemplo
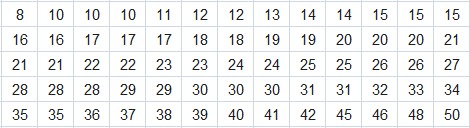
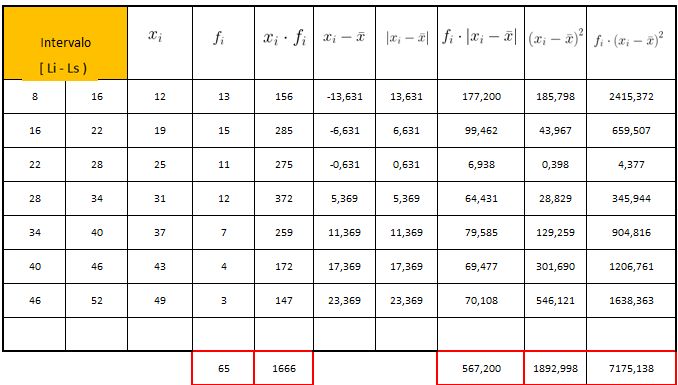
 Los resultados de las medidas de dispersión ofrecen una imagen clara de la variabilidad en sus trayectos:
Los resultados de las medidas de dispersión ofrecen una imagen clara de la variabilidad en sus trayectos: La desviación estándar de 10,5 minutos es relativamente alta en comparación con el promedio del tiempo de 43 minutos ya que representa un 41% de la media. Esto quiere decir que existe una gran dispersión en los tiempos individuales.
La desviación estándar de 10,5 minutos es relativamente alta en comparación con el promedio del tiempo de 43 minutos ya que representa un 41% de la media. Esto quiere decir que existe una gran dispersión en los tiempos individuales.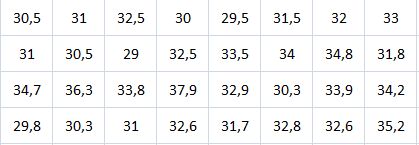

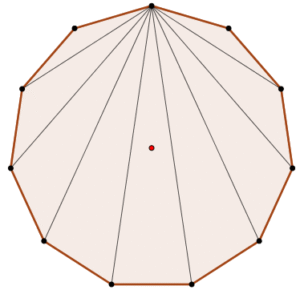
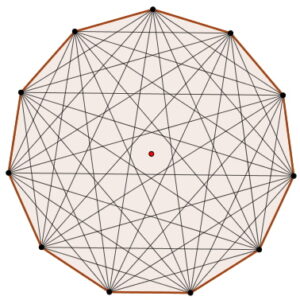
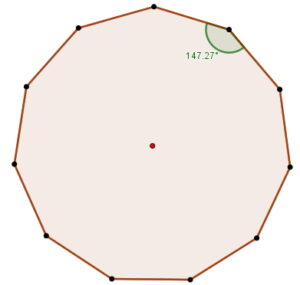
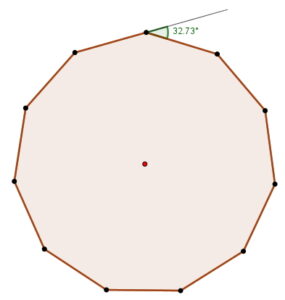
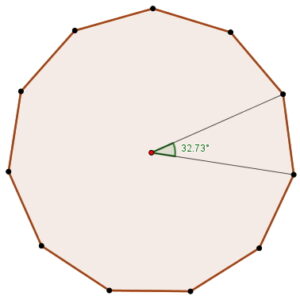
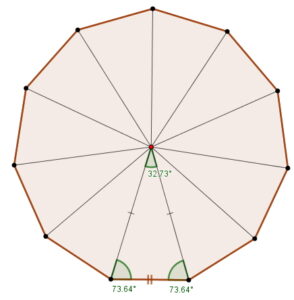
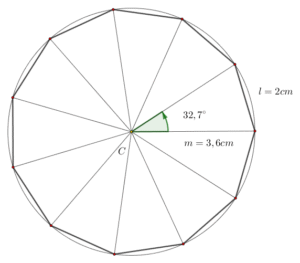
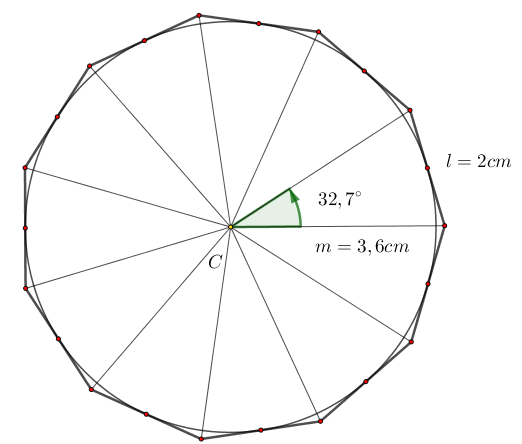
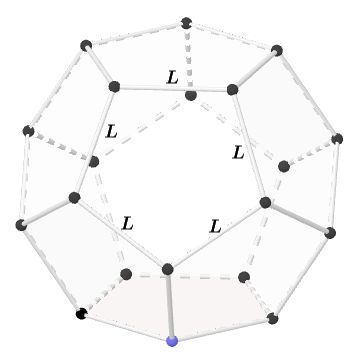
 ¿Sabías que las figuras geométricas están presentes en casi todo lo que nos rodea? El undecágono regular, aunque poco común, se esconde en muchos lugares: en el diseño de logotipos, en patrones de mosaicos, en la estructura de algunos estadios o incluso en gráficos digitales de videojuegos. Comprender cómo se define y se construye esta figura no solo fortalece tus habilidades geométricas, sino que también te permite apreciar la precisión y belleza que la matemática aporta al arte, la tecnología y la vida cotidiana. En este post descubrirás qué es un undecágono regular y cómo construirlo paso a paso, usando tus instrumentos de geometría y además el software de GeoGebra, con la precisión de un verdadero diseñador.
¿Sabías que las figuras geométricas están presentes en casi todo lo que nos rodea? El undecágono regular, aunque poco común, se esconde en muchos lugares: en el diseño de logotipos, en patrones de mosaicos, en la estructura de algunos estadios o incluso en gráficos digitales de videojuegos. Comprender cómo se define y se construye esta figura no solo fortalece tus habilidades geométricas, sino que también te permite apreciar la precisión y belleza que la matemática aporta al arte, la tecnología y la vida cotidiana. En este post descubrirás qué es un undecágono regular y cómo construirlo paso a paso, usando tus instrumentos de geometría y además el software de GeoGebra, con la precisión de un verdadero diseñador.
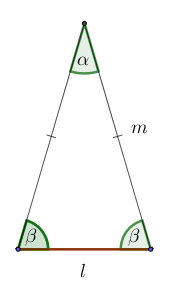 Donde:
Donde: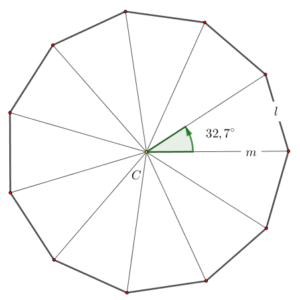
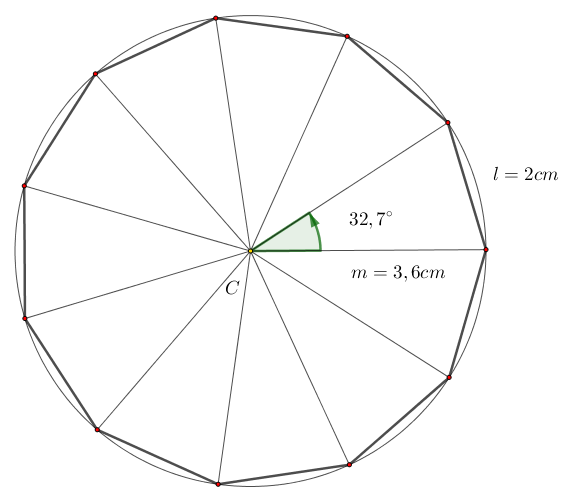
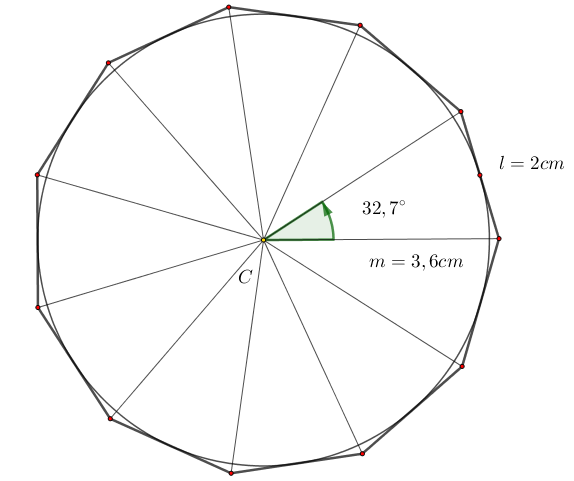

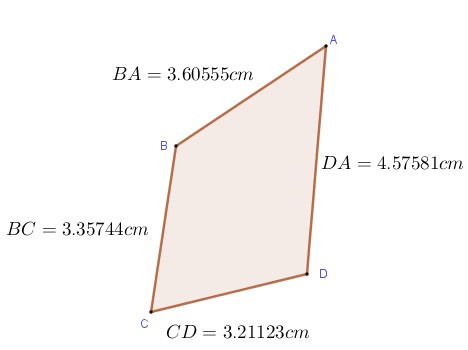
 ¿Quieres saber más de aproximación numérica? ¿Alguna vez has notado que, al dividir, tu calculadora a veces «corta» los números? O, ¿has visto que al comprar alguna cosa, los precios no siempre son exactos hasta el último decimal? ¡Pues no es magia! Detrás de esas situaciones cotidianas se esconden dos trucos matemáticos que usamos sin darnos cuenta todo el tiempo: el redondeo y el truncamiento.
¿Quieres saber más de aproximación numérica? ¿Alguna vez has notado que, al dividir, tu calculadora a veces «corta» los números? O, ¿has visto que al comprar alguna cosa, los precios no siempre son exactos hasta el último decimal? ¡Pues no es magia! Detrás de esas situaciones cotidianas se esconden dos trucos matemáticos que usamos sin darnos cuenta todo el tiempo: el redondeo y el truncamiento.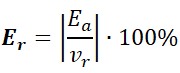
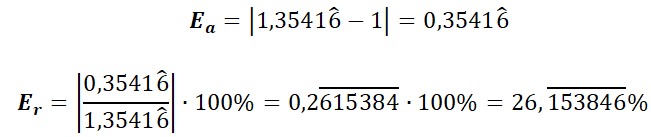

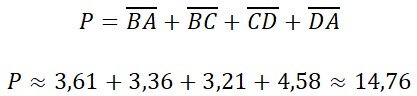
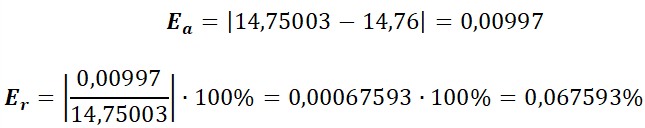


 ¿Quieres conocer más acerca del Teorema de Euclides? ¿Sabías que uno de los teoremas más antiguos de la geometría todavía se usa en cosas tan cotidianas como construir un edificio, diseñar videojuegos o resolver un rompecabezas? El Teorema de Euclides no es solo parte de un libro viejo de matemáticas: ¡está más vivo que nunca en nuestra vida diaria!
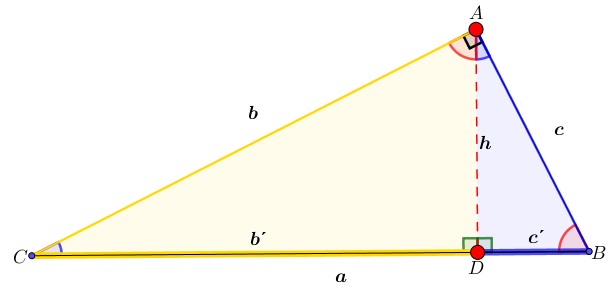
¿Quieres conocer más acerca del Teorema de Euclides? ¿Sabías que uno de los teoremas más antiguos de la geometría todavía se usa en cosas tan cotidianas como construir un edificio, diseñar videojuegos o resolver un rompecabezas? El Teorema de Euclides no es solo parte de un libro viejo de matemáticas: ¡está más vivo que nunca en nuestra vida diaria! Conocido como el padre de la geometría, fue un matemático Griego que vivió en Egipto hace más de 2000 años, alrededor del año 300 a.C. Gracias a sus investigaciones y demostraciones fue posible la creación de teoremas en los triángulos rectángulos.
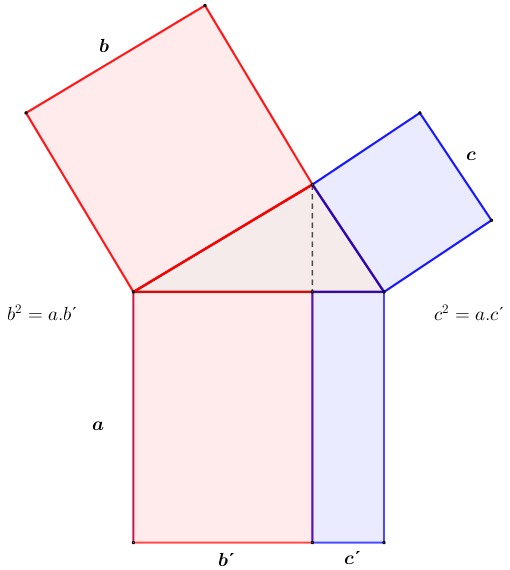
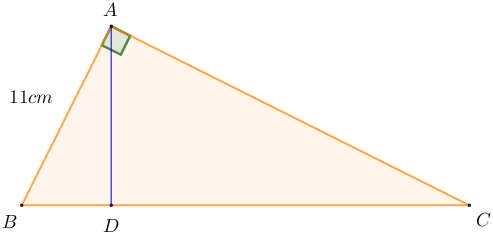
Conocido como el padre de la geometría, fue un matemático Griego que vivió en Egipto hace más de 2000 años, alrededor del año 300 a.C. Gracias a sus investigaciones y demostraciones fue posible la creación de teoremas en los triángulos rectángulos. Un
Un 


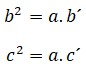


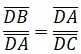

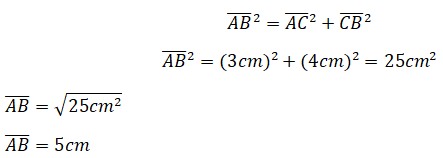
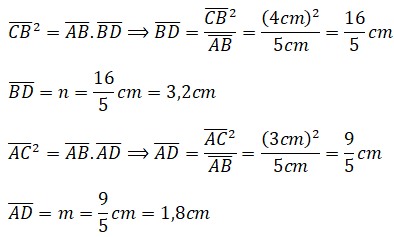

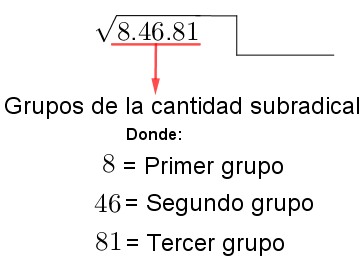
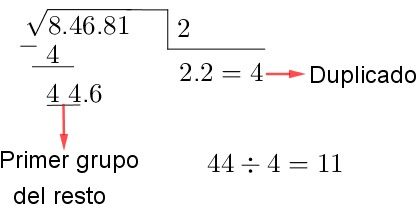
 ¿Sabías que puedes calcular la raíz cuadrada sin calculadora y sin sufrir en el intento? ¡Sí, es posible! Aprender este truco no solo es útil en matemáticas, sino que también te hará ver genial cuando sorprendas a tus amigos. Reflexiona en esto: siempre existen momento en la vida diaria donde no contamos con una calculadora y necesitamos resolver problemas rápido. Con este método divertido y efectivo, podrás calcular raíces cuadradas sin depender de la tecnología.
¿Sabías que puedes calcular la raíz cuadrada sin calculadora y sin sufrir en el intento? ¡Sí, es posible! Aprender este truco no solo es útil en matemáticas, sino que también te hará ver genial cuando sorprendas a tus amigos. Reflexiona en esto: siempre existen momento en la vida diaria donde no contamos con una calculadora y necesitamos resolver problemas rápido. Con este método divertido y efectivo, podrás calcular raíces cuadradas sin depender de la tecnología.


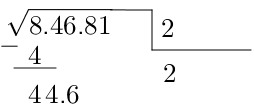





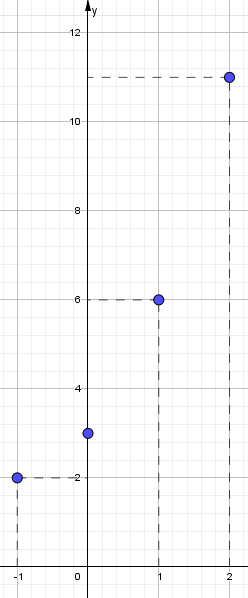
 ¿Sabías que la función cuadrática está presente en la vida diaria? Esto es, desde la trayectoria de un balón hasta el diseño de puentes. Graficar parábolas no solo es una habilidad matemática, sino también una forma divertida de visualizar cómo cambian las ecuaciones cuadráticas en el plano cartesiano. Si quieres profundizar en este fascinante tema, te invito que leas este post y aprenderás paso a paso desde la identificación de una parábola hasta graficarla de forma correcta.
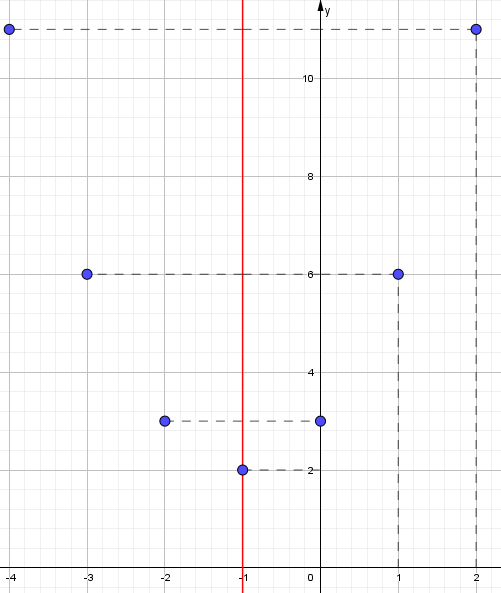
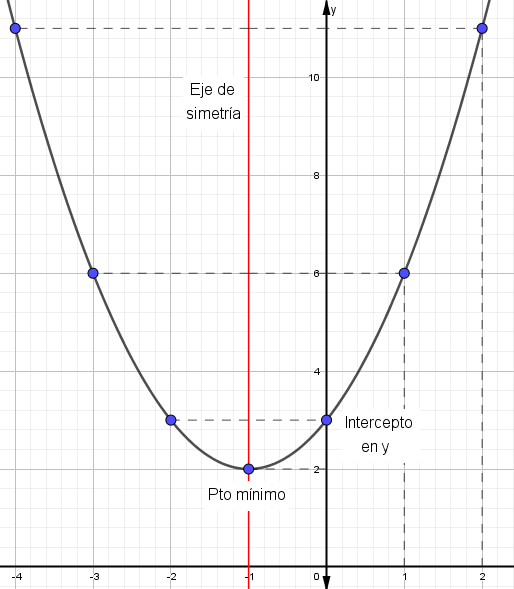
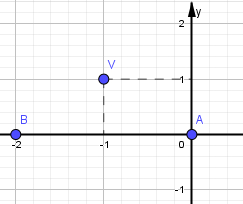
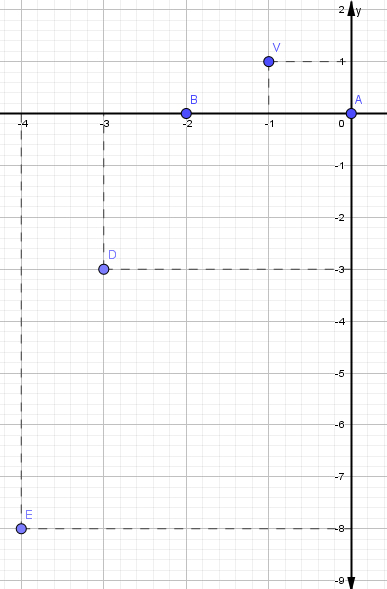
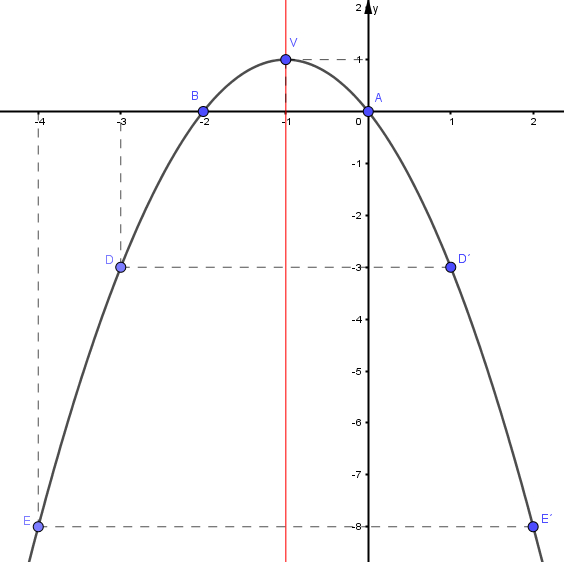
¿Sabías que la función cuadrática está presente en la vida diaria? Esto es, desde la trayectoria de un balón hasta el diseño de puentes. Graficar parábolas no solo es una habilidad matemática, sino también una forma divertida de visualizar cómo cambian las ecuaciones cuadráticas en el plano cartesiano. Si quieres profundizar en este fascinante tema, te invito que leas este post y aprenderás paso a paso desde la identificación de una parábola hasta graficarla de forma correcta.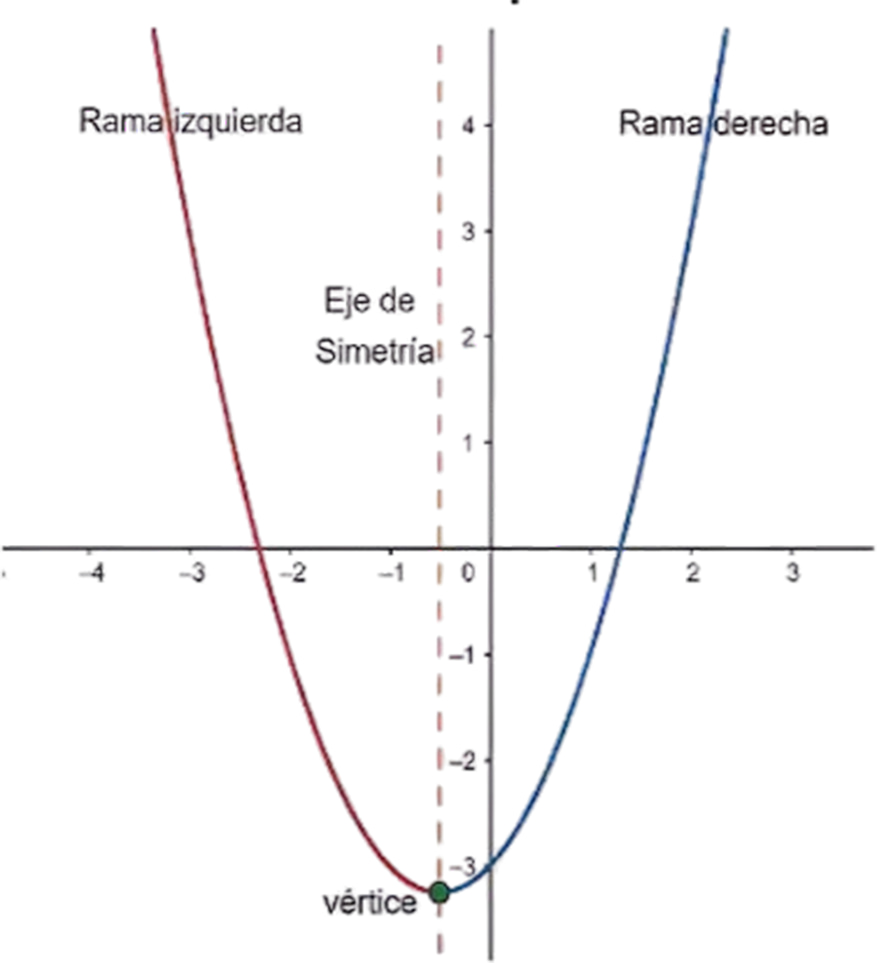 Es muy importante conocer las características de la parábola, ya que permite analizar su comportamiento y su representación gráfica. A continuación, sus características:
Es muy importante conocer las características de la parábola, ya que permite analizar su comportamiento y su representación gráfica. A continuación, sus características: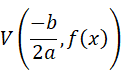
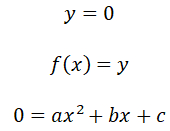
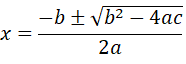
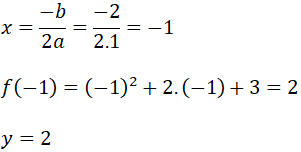
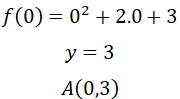
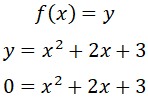
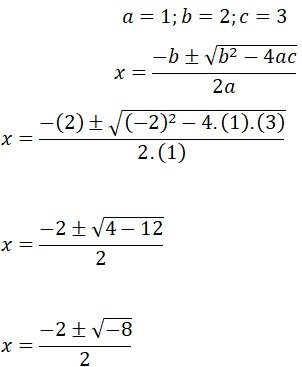
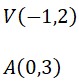
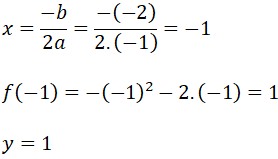
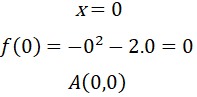
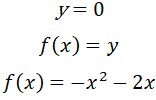
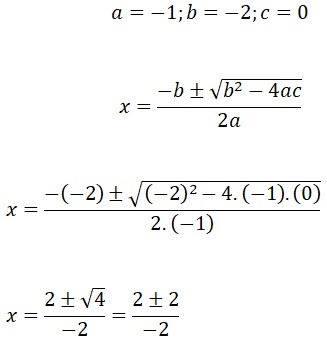
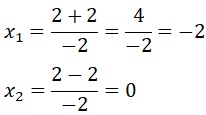
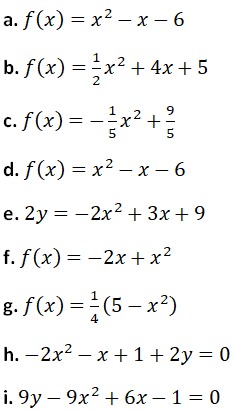

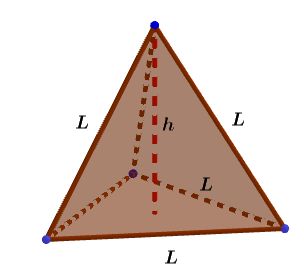
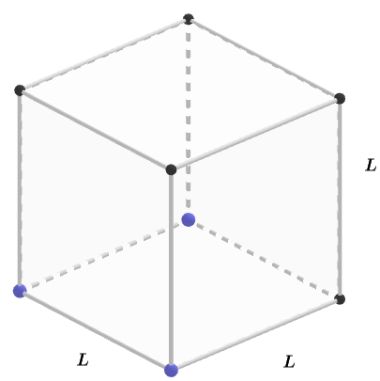
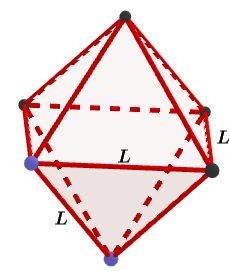
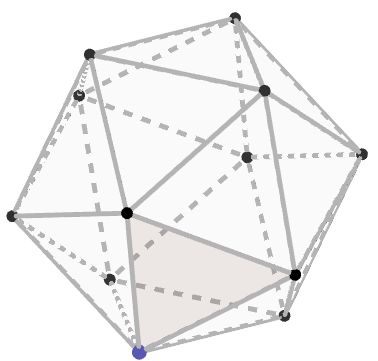
 Si estás buscando el cálculo de área y volumen de un poliedro regular estás en el lugar correcto. Comencemos con este ejemplo de la vida diaria: El señor Rafael es un diseñador de interiores, en su último contrato tuvo que remodelar un apartamento pequeño. El cliente le exigió un diseño moderno y funcional con la intención de aprovechar al máximo los espacios de las paredes, techos y rincones. Para ello, calculó con precisión las áreas y volúmenes de diferentes elementos decorativos, para así asegurarse que todos encajen sin desperdiciar espacios. Finalmente seleccionó los muebles, camas y comedor con una estética agradable y ajustada a la comodidad del paso en el lugar.
Si estás buscando el cálculo de área y volumen de un poliedro regular estás en el lugar correcto. Comencemos con este ejemplo de la vida diaria: El señor Rafael es un diseñador de interiores, en su último contrato tuvo que remodelar un apartamento pequeño. El cliente le exigió un diseño moderno y funcional con la intención de aprovechar al máximo los espacios de las paredes, techos y rincones. Para ello, calculó con precisión las áreas y volúmenes de diferentes elementos decorativos, para así asegurarse que todos encajen sin desperdiciar espacios. Finalmente seleccionó los muebles, camas y comedor con una estética agradable y ajustada a la comodidad del paso en el lugar.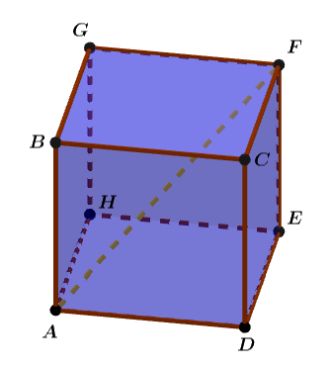
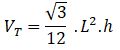
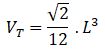
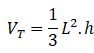
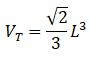
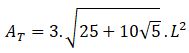
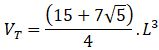
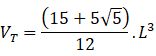
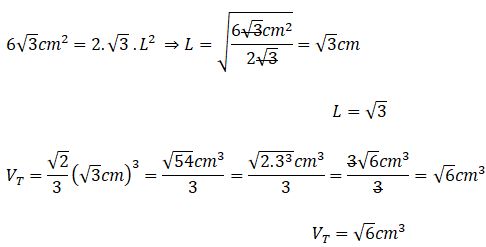
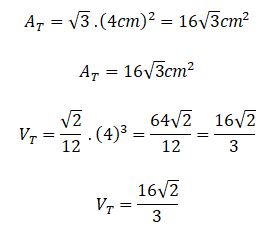
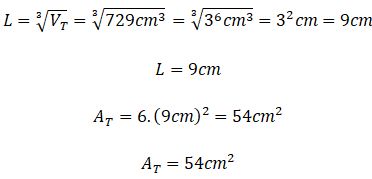
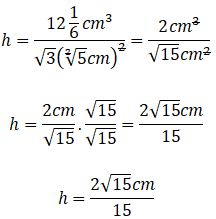

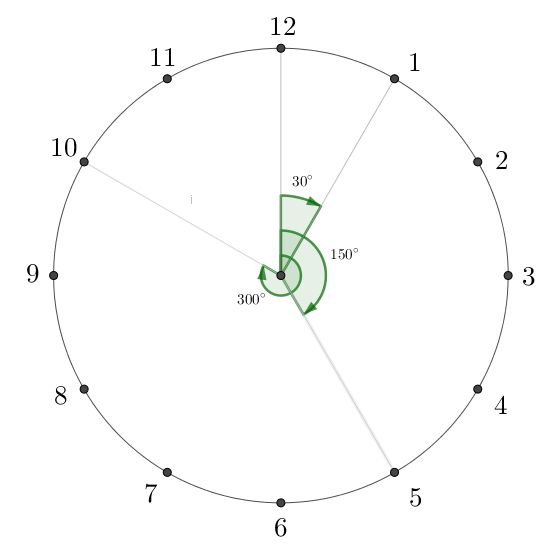
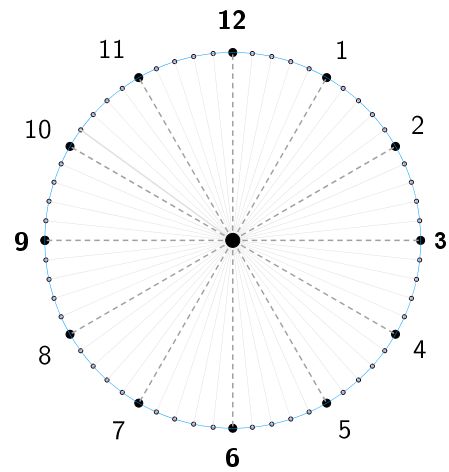
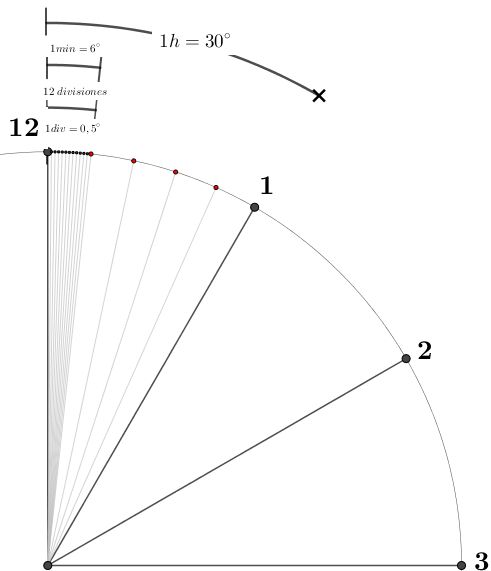
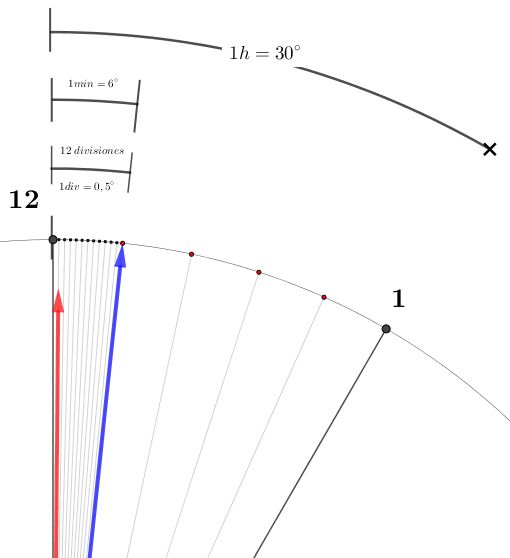
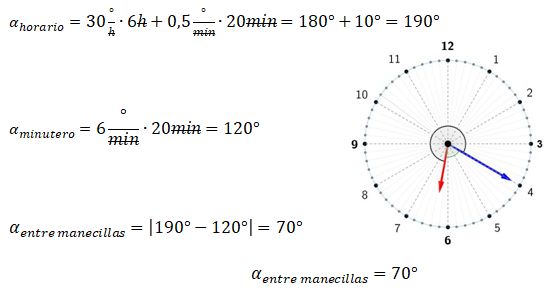
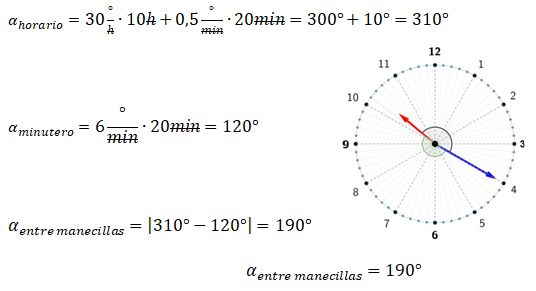
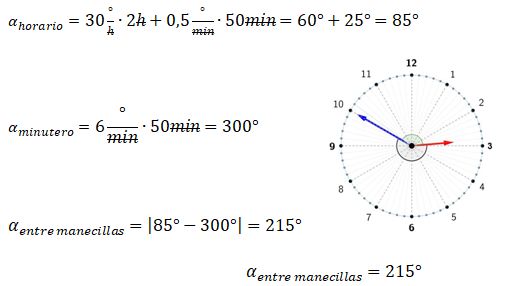
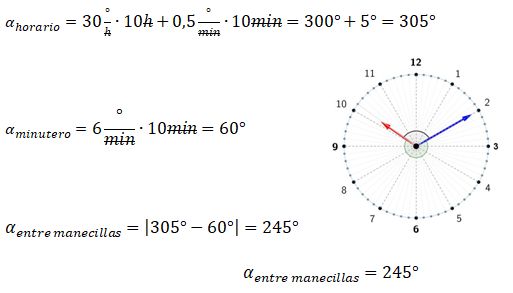
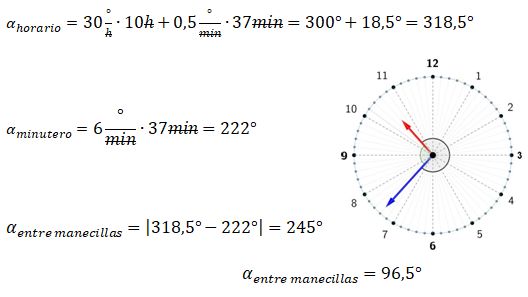
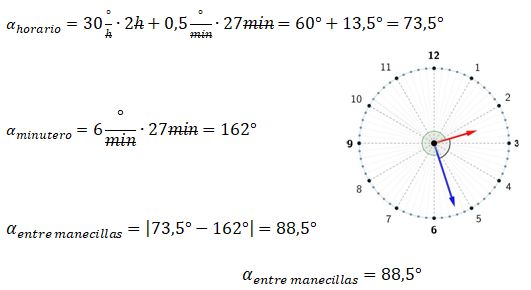
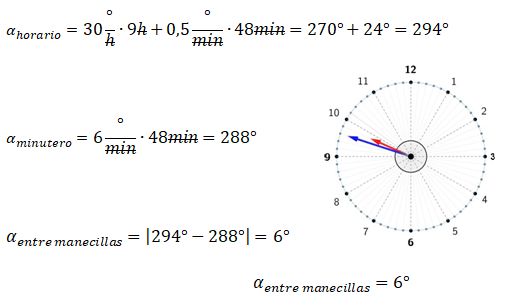
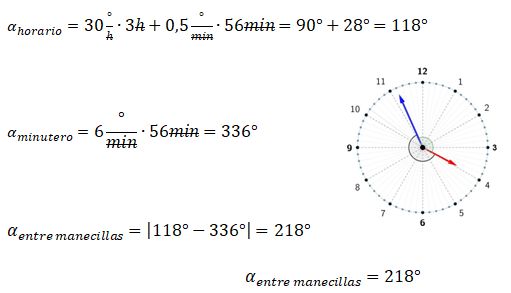
 ¿Sabes cómo calcular el ángulo entre las manecillas de un reloj análogo? Si quieres conocer más acerca de este tema, aquí te lo explicamos paso a paso. Como bien sabes, la función principal de un reloj analógico es mostrar el tiempo. Sin embargo, gracias a sus manecillas también se puede observar los ángulos que estas forman en cualquier instante. El reloj no solo permite leer la hora, sino también permite entender la relación entre el tiempo y los ángulos.
¿Sabes cómo calcular el ángulo entre las manecillas de un reloj análogo? Si quieres conocer más acerca de este tema, aquí te lo explicamos paso a paso. Como bien sabes, la función principal de un reloj analógico es mostrar el tiempo. Sin embargo, gracias a sus manecillas también se puede observar los ángulos que estas forman en cualquier instante. El reloj no solo permite leer la hora, sino también permite entender la relación entre el tiempo y los ángulos.