El método de sustitución es otra manera de poder resolver un sistema de ecuaciones lineales con dos incógnitas. Así que, quédate en este post que te ayudará a resolver fácilmente este método.
El método de sustitución es otra manera de poder resolver un sistema de ecuaciones lineales con dos incógnitas. Así que, quédate en este post que te ayudará a resolver fácilmente este método.
Como su nombre lo indica se trata de sustituir para poder hallar la solución.
| El método de sustitución consiste en despejar una incógnita de cualquier ecuación y luego sustituir su valor en la otra, obteniéndose una nueva ecuación de una sola incógnita. |
Pasos para aplicar el método de sustitución
- Seleccionar una ecuación.
- Realizar el despeje de cualquier variable “x” e “y”
- Sustituir la expresión de esa variable en la otra ecuación.
- Sustituir el valor encontrado en cualquier ecuación dada.
- Comprobación.
- Tipo de sistema.
Ejercicios resueltos de método de sustitución
Para resolver tus habilidades en este tema, te invitamos a ver los siguientes ejemplos resueltos paso a paso:
Ejemplo # 1
Resolver el siguiente sistema de ecuaciones aplicando el método de sustitución y diga el nombre del sistema.
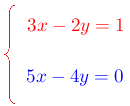
Solución
Paso # 1. Seleccionar una ecuación.
En este caso se escoge la primera ecuación que es:
![]()
Paso # 2. Despejar.
Para este ejemplo se despeja la “x”
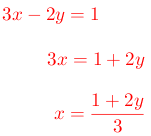
Paso # 3. Sustituir la expresión de esa variable en la otra ecuación.
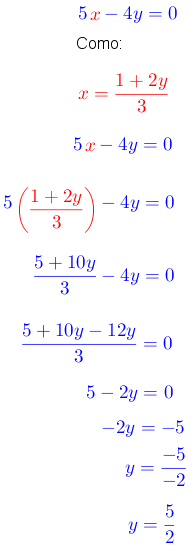
Paso # 4. Sustituir el valor encontrado en cualquier ecuación dada.
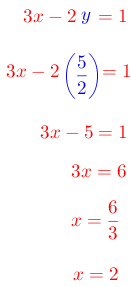
Paso # 5. Comprobación.
Se sustituye los valores encontrados de x e y en cualquier ecuación para comprobar si es correcto sus resultados. Para este ejemplo se selecciona la segunda ecuación.
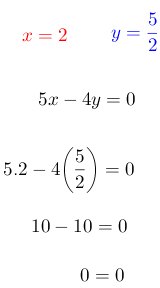
Como el resultado es igual, los valores de “x” e “y” es correcto.
Paso # 6. El tipo de sistema es un compatible determinado ya que tiene una solución.
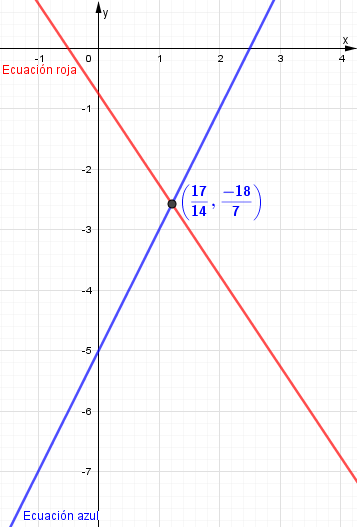
Punto de intersección de ambas rectas es:
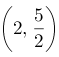
Ejemplo # 2
Resolver el siguiente sistema de ecuaciones aplicando el método de sustitución y diga el nombre del sistema.
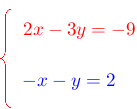
Solución
Paso # 1. Seleccionar una ecuación.
En este caso se escoge la segunda ecuación.
![]()
Paso # 2. Despejar.
Para este ejemplo se despeja la variable “y”
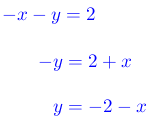
Paso # 3. Sustituir la expresión en la otra ecuación.
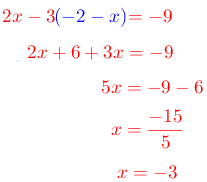
Paso # 4. Sustituir el valor encontrado en cualquier ecuación.
Para este caso se selecciona la segunda ecuación.
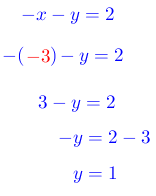
Paso # 5. Comprobación.
Se sustituye los valores encontrados de x e y en cualquier ecuación para comprobar si es correcto sus resultados. Para este ejemplo se selecciona la primera ecuación.
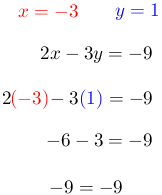
Como el resultado es igual, los valores de “x” e “y” es correcto.
Paso # 6. El tipo de sistema es un compatible determinado ya que tiene una solución.
Punto de intersección de ambas rectas es:
(-3,1)
Ejemplo # 3
Resolver el siguiente sistema de ecuaciones aplicando el método de sustitución y diga el nombre del sistema.
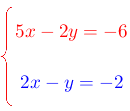
Solución
Paso # 1. Seleccionar una ecuación.
En este caso se toma la primera ecuación.
![]()
Paso # 2. Despejar.
Para este ejemplo se despeja la variable “x”
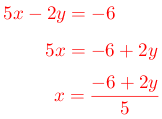
Paso # 3. Sustituir la expresión en la otra ecuación.
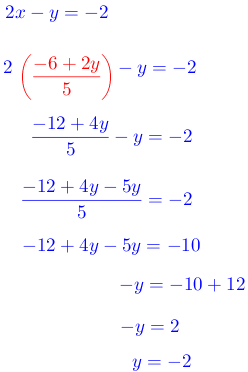
Paso # 4. Sustituir el valor encontrado en cualquier ecuación.
Para este caso se selecciona la primera ecuación.
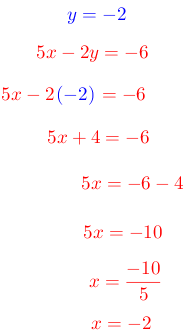
Paso # 5. Comprobación.
Se sustituye los valores encontrados de x e y en cualquier ecuación para comprobar si es correcto sus resultados. Para este ejemplo se selecciona la segunda ecuación.
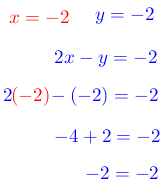
Como el resultado es idéntico los valores de “x” e “y” es correcto.
Paso # 6. El tipo de sistema es un compatible determinado ya que tiene una solución.
Punto de intersección de ambas rectas es:
(-2,-2)
¿Quieres practicar más con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
Actividades
Utiliza el método de sustitución para determinar las soluciones a los siguientes sistemas de ecuaciones y diga el nombre del sistema.
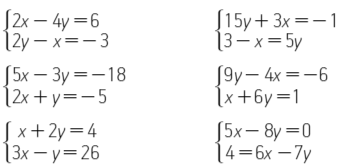
Determina los valores de los valores de los coeficientes A y B para que el sistema de ecuaciones tenga la solución indicada.

Si quieres ver más contenido como este, no dejes de compartir con tus amigos y familiares. También te pedimos que nos dejes un comentario acerca de este contenido.

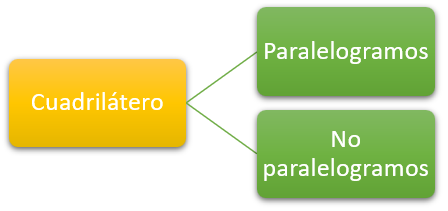
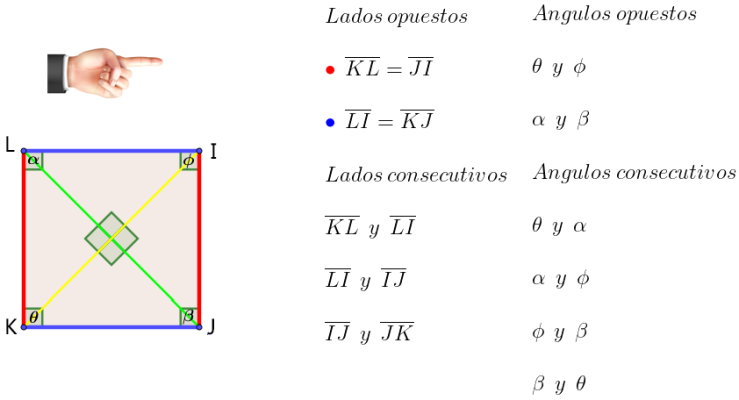
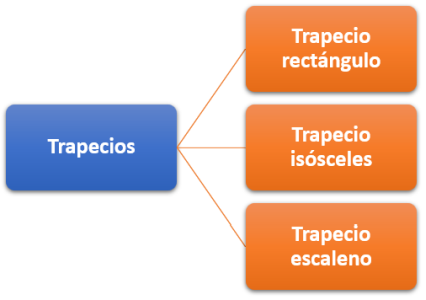
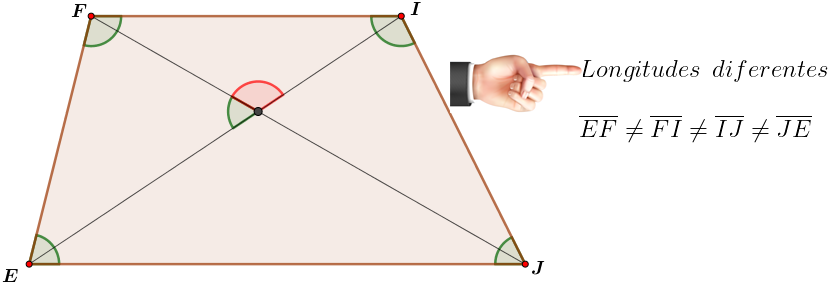
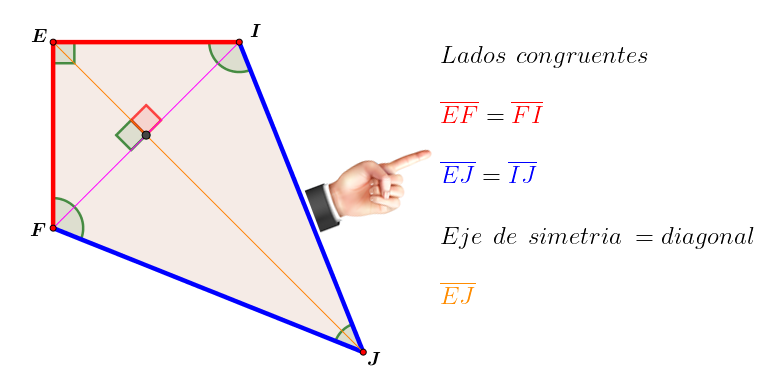
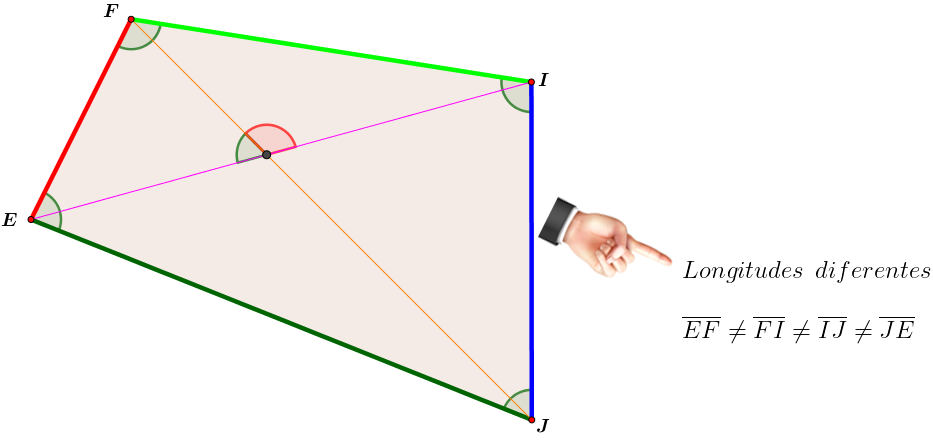
 ¿Te has preguntado alguna vez qué son los cuadriláteros y por qué aparecen tan seguido en tu entorno?
¿Te has preguntado alguna vez qué son los cuadriláteros y por qué aparecen tan seguido en tu entorno?

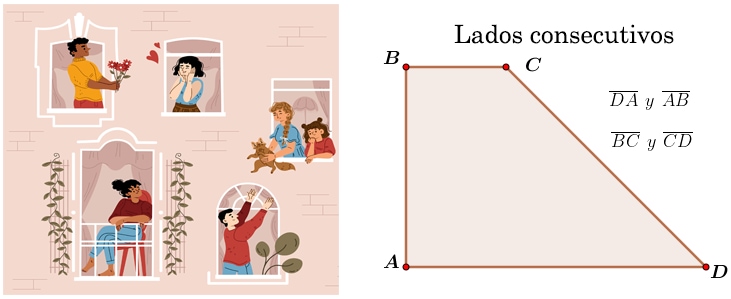
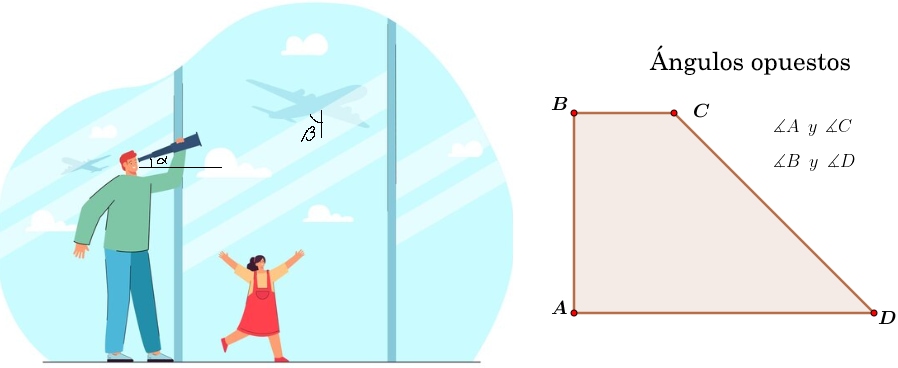








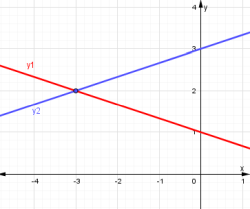 ¿Estás estudiando sistema de ecuaciones y buscas una manera fácil de resolver el método de igualación? Sí es así, has llegado al lugar indicado. Antes de comenzar el método de igualación, reforcemos en qué consiste el método gráfico, ya que ayuda a ver el punto de intersección de las rectas. Sin embargo, cuando el resultado son números reales el método en muchas ocasiones no admite ver el punto de coordenada con precisión.
¿Estás estudiando sistema de ecuaciones y buscas una manera fácil de resolver el método de igualación? Sí es así, has llegado al lugar indicado. Antes de comenzar el método de igualación, reforcemos en qué consiste el método gráfico, ya que ayuda a ver el punto de intersección de las rectas. Sin embargo, cuando el resultado son números reales el método en muchas ocasiones no admite ver el punto de coordenada con precisión.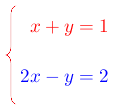
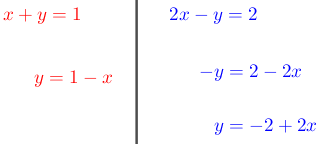
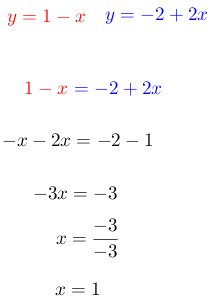
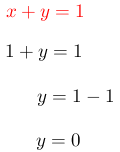
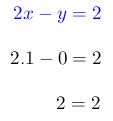

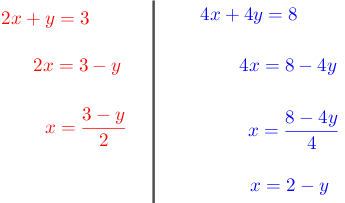
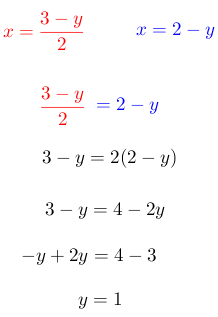
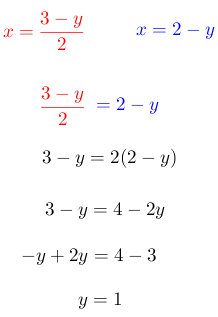
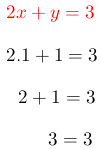


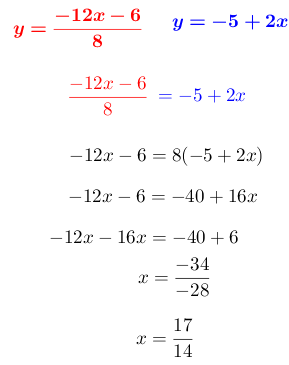

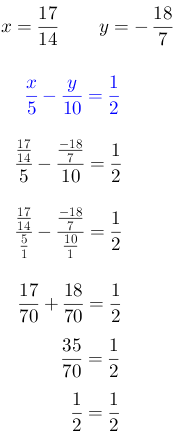

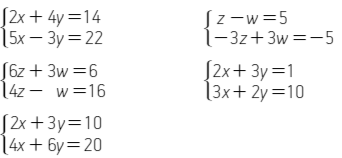
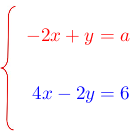

 ¿Sabías que la suma y resta de monomios están presentes en problemas reales de ingeniería, economía e incluso tecnología?
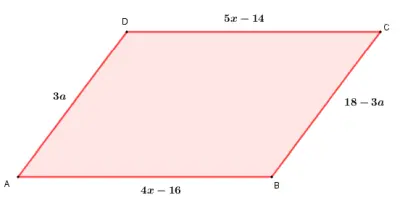
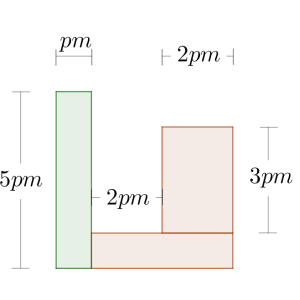
¿Sabías que la suma y resta de monomios están presentes en problemas reales de ingeniería, economía e incluso tecnología? Determinar el perímetro del siguiente romboide.
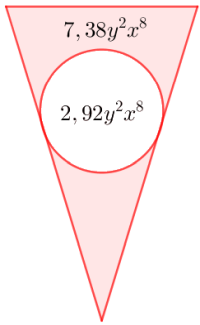
Determinar el perímetro del siguiente romboide.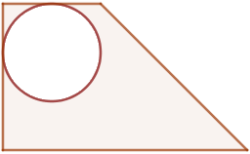 Determinar el área de la región coloreada, sabiendo que el área del trapecio rectangular es AT = 10,5 d4e6 y el área del círculo AC = 3,14 d4e6.
Determinar el área de la región coloreada, sabiendo que el área del trapecio rectangular es AT = 10,5 d4e6 y el área del círculo AC = 3,14 d4e6.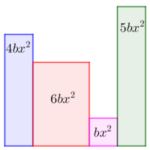
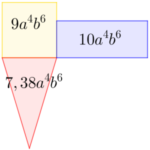
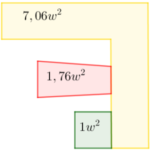
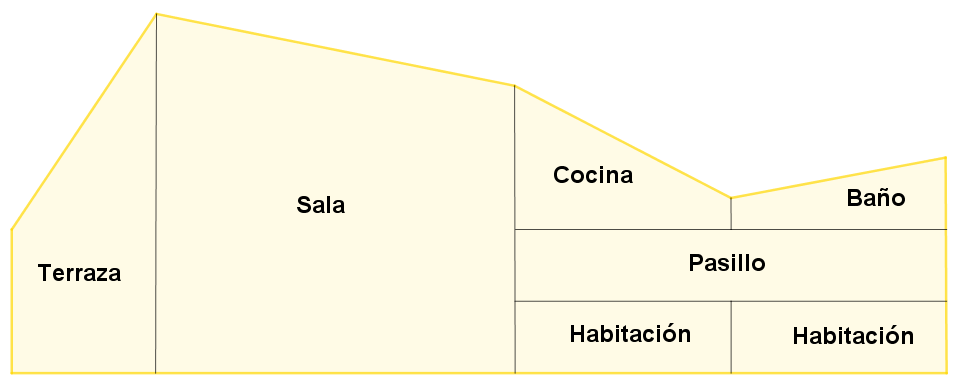
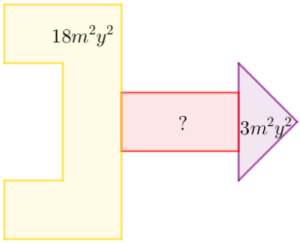 El área total de la siguiente imagen es de 27m2y2. Calcula la región desconocida y selecciona la opción correcta.
El área total de la siguiente imagen es de 27m2y2. Calcula la región desconocida y selecciona la opción correcta.