¿Te ha pasado que en clase de trigonometría te piden demostraciones de identidades trigonométricas y no sabes por dónde empezar? 😅
¿Te ha pasado que en clase de trigonometría te piden demostraciones de identidades trigonométricas y no sabes por dónde empezar? 😅
No estás solo. Entender las demostraciones de identidades trigonométricas no se trata solo de memorizar fórmulas, sino de razonar con lógica matemática. En este artículo descubrirás cómo convertir un problema complejo en una demostración sencilla, paso a paso, con ejemplos claros que podrás aplicar en tus próximos exámenes.
¿Qué significa las demostraciones de identidades trigonométricas?
Las demostraciones de identidades trigonométricas son un proceso matemático que busca comprobar que dos expresiones trigonométricas son equivalentes para cualquier valor del ángulo, el procedimiento es único según la identidad.
Estos tipos de ejercicios fortalecen tu razonamiento lógico y tu dominio de las propiedades del seno, coseno y otras funciones trigonométricas.
¿Qué son las identidades trigonométricas y para qué sirven?
Las identidades trigonométricas son igualdades entre funciones trigonométricas que se cumplen para cualquier valor del ángulo. Son esenciales porque permiten simplificar expresiones, resolver ecuaciones trigonométricas y analizar fenómenos periódicos en física e ingeniería.
Ejemplo:
$$sen^{2}\alpha +cos^{2}\alpha =1$$
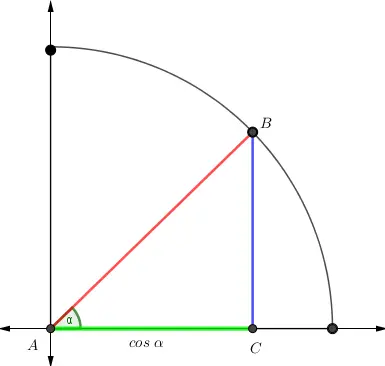
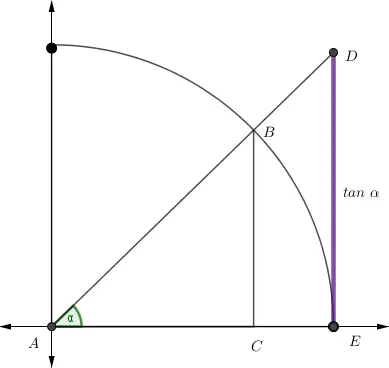
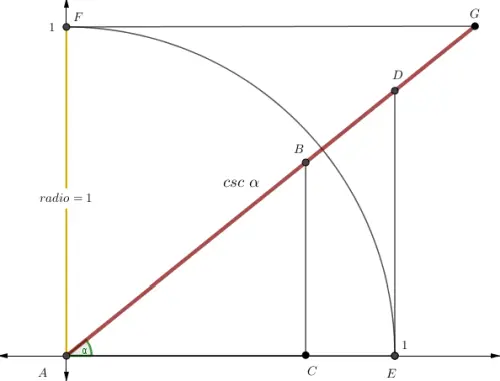
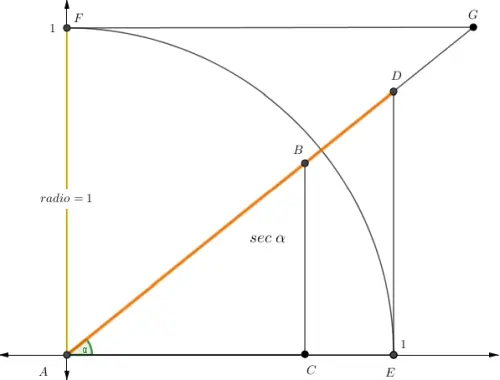
Esta identidad puede comprobarse con el Teorema de Pitágoras aplicado a la Circunferencia trigonométrica.
Tipos principales de identidades trigonométricas
Ellas son:
- Recíprocas.
- Cociente.
- Pitagóricas.
- De cofunción y doble ángulo.
Observa la siguientes tabla:
Identidades recíprocas | Identidades de cociente | Identidades pitagóricas |
| $$sen\alpha =\frac{1}{csc\alpha }$$ | $$tan\alpha =\frac{sen\alpha }{cos\alpha }$$ | $$sen^{2}\alpha +cos^{2}\alpha =1$$ |
| $$cos\alpha =\frac{1}{sec\alpha }$$ | $$cot\alpha =\frac{cos\alpha }{sen\alpha }$$ | $$sen\alpha =\pm \sqrt{1-cos^{2}\alpha }$$ |
| $$tan\alpha =\frac{1}{cot\alpha }$$ | $$cos\alpha =\pm \sqrt{1-sen^{2}\alpha }$$ | |
| $$csc\alpha =\frac{1}{sen\alpha }$$ | $$tan^{2}\alpha=sec^{2} \alpha-1$$ | |
| $$sec\alpha =\frac{1}{cos\alpha }$$ | $$sec\alpha =\pm \sqrt{tan^{2}\alpha +1}$$ | |
| $$cot\alpha =\frac{1}{tan\alpha }$$ | $$cot^{2}x\alpha =csc^{2}x-1$$ | |
| $$csc\alpha =\pm \sqrt{ctg^{2}\alpha +1}$$ |
¿Cómo demostrar identidades trigonométricas paso a paso?
Te daré 7 estrategias valiosas para que seas un experto demostrando identidades trigonométrica, ellas son las siguientes:
Memoriza bien las identidades trigonométricas básicas
Antes de comenzar, asegúrate de dominar las identidades recíprocas, pitagóricas y de cociente. Son los pilares fundamentales sobre los que se construyen todas las demostraciones. Tenerlas claras te dará una base sólida para cualquier transformación.
Elige el lado de la ecuación adecuada para iniciar
Por lo general, es más fácil comenzar trabajando con el lado más complejo de la identidad. Este lado suele ofrecer más oportunidades para aplicar identidades y simplificar expresiones hasta que coincida con el lado más sencillo. Sin embargo, no dudes en trabajar en ambos lados simultáneamente si el problema lo requiere, buscando un punto medio donde ambos se igualen.
Transforma a seno y coseno
Cuando te encuentres «atascado» o la expresión parezca demasiado complicada, un excelente primer paso es reescribir todas las funciones trigonométricas en términos de seno y coseno. Esto a menudo simplifica la expresión y te permite ver nuevas oportunidades para aplicar identidades o realizar operaciones algebraicas.
Visión algebraica
Las demostraciones de identidades trigonométricas también son un ejercicio de álgebra. No olvides aplicar tus habilidades en:
- Factorización (factores comunes o usar diferencias de cuadrados)
- Productos notables.
- Propiedad distributiva.
- Productos de binomios.
- Suma y Resta de Fracciones.
- Simplificación para cancelar términos o reducir expresiones.
- Racionalización.
Multiplicar por 1
En algunos momentos es clave multiplicar por 1 cuando necesitas crear un denominador o numerador específico. Por ejemplo:
$$\frac{1-senx}{cosx}\cdot \frac{1+senx}{1+senx}$$
Simplifica siempre que puedas
El objetivo final es llegar a una expresión idéntica en ambos lados. Después de cada paso, revisa si puedes simplificar la expresión resultante. Eliminar términos innecesarios te acercará a la solución y evitará que la demostración se complique más de lo necesario.
¡La Práctica Hace al Maestro!
La habilidad para demostrar identidades trigonométricas se desarrolla con la práctica constante. No te desanimes si un ejercicio no sale a la primera; cada intento te enseña algo nuevo y fortalece tu intuición matemática. Disfruta el proceso de desentrañar cada problema.
35 ejercicios de demostraciones de Identidades Trigonométricas resueltos paso a paso
 Te recomiendo que soluciones cada ejercicio por tu propia cuenta. Una vez que lo hayas intentado, o si te sientes atascado, entonces sí, compara tu procedimiento y resultado con nuestra guía. Si te encuentras con un bloqueo, esfuérzate un poquito más antes de mirar la solución; ese es el momento clave donde tu comprensión realmente se afianza. Si aún así no lo logras, no te preocupes, observa el procedimiento detallado. ¡Esta guía es una herramienta indispensable que te permitirá comprender, practicar y dominar las demostraciones, ganando habilidades matemáticas esenciales que te servirán en muchas otras situaciones!
Te recomiendo que soluciones cada ejercicio por tu propia cuenta. Una vez que lo hayas intentado, o si te sientes atascado, entonces sí, compara tu procedimiento y resultado con nuestra guía. Si te encuentras con un bloqueo, esfuérzate un poquito más antes de mirar la solución; ese es el momento clave donde tu comprensión realmente se afianza. Si aún así no lo logras, no te preocupes, observa el procedimiento detallado. ¡Esta guía es una herramienta indispensable que te permitirá comprender, practicar y dominar las demostraciones, ganando habilidades matemáticas esenciales que te servirán en muchas otras situaciones!
Ejercicio # 1
$$\frac{senx+tanx}{1+cosx}=tanx$$
Solución:
$$\frac{senx+tanx}{1+cosx}=tanx$$
$$\frac{senx+\frac{senx}{cosx}}{1+cosx}=tanx$$
$$\frac{\frac{senxcosx+senx}{cosx}}{1+cosx}=tanx$$
$$\frac{senxcosx+senx}{cosx(1+cosx)}=tanx$$
$$\frac{senx(cosx+1)}{cosx(cosx+1)}=tanx$$
$$\frac{senx}{cosx}=tanx$$
$$tanx=tanx$$
Ejercicio # 2
$$\frac{1+tan^2 x}{csc^2 x}=tan^2 x$$
Solución:
$$\frac{1+tan^2 x}{csc^2 x}=tan^2 x$$
$$\frac{1+\frac{sen^2 x}{cos^2 x}}{\frac{1}{sen^2 x} x}=tan^2 x$$
$$\frac{sen^2 x(cos^2 x +sen^2 x)}{cos^2 x}=tan^2 x$$
$$\frac{sen^2 x}{cos^2 x}=tan^2 x$$
$$tan^2 x=tan^2 x$$
Ejercicio # 3
$$\frac{1-cos^{2}x}{tan^{2}x}=cos^2 x$$
Solución:
$$\frac{1-cos^{2}x}{tan^{2}x}=cos^2 x$$
$$\frac{1-cos^{2}x}{\frac{sen^{2}x}{cos^{2}x}}=cos^{2}x$$
$$\frac{(1-cos^{2}x)\cdot cos^{2}x}{sen^{2}x}=cos^2x$$
$$\frac{sen^{2}x\cdot cos^{2}x}{sen^{2}x}=cos^2x$$
$$cos^{2}x=cos^2x$$
Ejercicio # 4
$$sec^{2}x+csc^{2}x = sec^{2}x\cdot csc^{2}x$$
Solución:
$$sec^{2}x+csc^{2}x = sec^{2}x\cdot csc^{2}x$$
$$ \frac{1}{cos^{2}x}+\frac{1}{sen^{2}x}=sec^{2}x\cdot csc^{2}x $$
$$ \frac{sen^{2}x+cos^{2}x}{cos^{2}x\cdot sen^{2}x}=sec^{2}x\cdot csc^{2}x$$
$$ \frac{1}{cos^{2}x\cdot sen^{2}x}=sec^{2}x\cdot csc^{2}x$$
$$ sec^{2}x\cdot csc^{2}x=sec^{2}x\cdot csc^{2}x$$
Ejercicio # 5
$$\frac{1+cosx}{senx}=\frac{senx}{1-cosx}$$
Solución:
$$\frac{1+cosx}{senx}=\frac{senx}{1-cosx}$$
$$\frac{(1+cosx)\cdot (1-cosx)}{senx\cdot (1-cosx)}=\frac{senx}{1-cosx} $$
$$\frac{1-cos^{2}x}{sen(1-cosx)}=\frac{senx}{1-cosx} $$
$$\frac{1-(1-sen^{2}x)}{sen(1-cosx)}=\frac{senx}{1-cosx} $$
$$\frac{1-1+sen^{2}x}{sen(1-cosx)}=\frac{senx}{1-cosx} $$
$$\frac{sen^{2}x}{senx(1-cosx)}=\frac{senx}{1-cosx} $$
$$\frac{senx}{1-cosx}=\frac{senx}{1-cosx} $$
Ejercicio # 6
$$\frac{1}{secx-1}+\frac{1}{secx+1}=2cotx\cdot cscx$$
Solución:
$$\frac{1}{secx-1}+\frac{1}{secx+1}=2cotx\cdot cscx$$
$$\frac{(secx+1)+(secx-1)}{sec^{2}x-1}=2cotx\cdot cscx$$
$$\frac{secx+1+secx-1}{sec^{2}x-1}=2cotx\cdot cscx$$
$$\frac{2secx}{sec^{2}x-1}=2cotx\cdot cscx$$
$$\frac{2secx}{1+tan^{2}x-1}=2cotx\cdot cscx$$
$$\frac{2secx}{tan^{2}x}=2cotx\cdot cscx$$
$$\frac{2\frac{1}{cosx}}{\frac{sen^{2}x}{cos^{2}x}}=2cotx\cdot cscx$$
$$\frac{\frac{2}{cosx}}{\frac{sen^{2}x}{cos^{2}x}}=2cotx\cdot cscx$$
$$\frac{2cos^{2}x}{cosx\cdot sen^{2}x}=2cotx\cdot cscx$$
$$\frac{2cosx}{senx\cdot senx}=2cotx\cdot cscx$$
$$2cotx\cdot \frac{1}{senx}=2cotx\cdot cscx$$
$$2cotx\cdot cscx=2cotx\cdot cscx$$
Ejercicio # 7
Solución:
$$ \frac{2cosx-senx-1}{cos^{2}x}=\frac{2cosx-senx-1}{cos^{2}x}$$
Ejercicio # 8
$$\frac{1+tanx}{1-tanx}=\frac{cotx+1}{cotx-1}$$
Solución:
$$\frac{1+tanx}{1-tanx}=\frac{cotx+1}{cotx-1}$$
$$ \frac{1+\frac{1}{cotx}}{1-\frac{1}{cotx}}=\frac{cotx+1}{cotx-1}$$
$$ \frac{\frac{cotx+1}{cotx}}{\frac{cotx-1}{cotx}}=\frac{cotx+1}{cotx-1}$$
$$ \frac{cotx+1}{cotx-1}=\frac{cotx+1}{cotx-1}$$
Ejercicio # 9
$$\frac{sen^{2}x+cos^{2}x}{tan^{2}x}=\frac{csc^{2}x}{sec^{2}x}$$
Solución:
$$\frac{sen^{2}x+cos^{2}x}{tan^{2}x}=\frac{csc^{2}x}{sec^{2}x}$$
$$\frac{sen^{2}x\cdot cos^{2}x+cos^{4}x}{sen^{2}x}=\frac{csc^{2}x}{sec^{2}x}$$
$$\frac{sen^{2}x(1-sen^{2}x)+cos^{4}x}{sen^{2}x}=\frac{csc^{2}x}{sec^{2}x}$$
$$\frac{sen^{2}x-sen^{4}x+(cos^{2}x)^{2}}{sen^{2}x}=\frac{csc^{2}x}{sec^{2}x}$$
$$\frac{sen^{2}x-sen^{4}x+(1-sen^{2})^{2}}{sen^{2}x}=\frac{csc^{2}x}{sec^{2}x}$$
$$\frac{1-sen^{2}x}{sen^{2}x}=\frac{csc^{2}x}{sec^{2}x}$$
$$\frac{cos^{2}x}{sen^{2}x}=\frac{csc^{2}x}{sec^{2}x}$$
$$\frac{csc^{2}x}{sec^{2}x}=\frac{csc^{2}x}{sec^{2}x}$$
Ejercicio # 10
$$secx-tanx=\frac{cosx}{1+senx}$$
Solución:
$$secx-tanx=\frac{cosx}{1+senx}$$
$$\frac{1}{cosx}-\frac{senx}{cosx}=\frac{cosx}{1+senx}$$
$$\frac{1-senx}{cosx}=\frac{cosx}{1+senx}$$
$$\frac{1-sen^{2}x}{cosx(1+senx)}=\frac{cosx}{1+senx}$$
$$\frac{1-(1-cos^{2}x)}{cosx(1+senx)}=\frac{cosx}{1+senx}$$
$$\frac{1-1+cos^{2}x)}{cosx(1+senx)}=\frac{cosx}{1+senx}$$
$$\frac{cos^{2}x}{cosx(1+senx)}=\frac{cosx}{1+senx}$$
$$\frac{cosx}{1+senx}=\frac{cosx}{1+senx}$$
Ejercicio # 11
$$\frac{2tanx}{1-tan^{2}x}=\frac{2}{cotx-tanx}$$
Solución:
$$\frac{2tanx}{1-tan^{2}x}=\frac{2}{cotx-tanx}$$
$$\frac{2tanx}{1-tan^{2}x}=\frac{2}{\frac{1}{tanx}-tanx}$$
$$\frac{2tanx}{1-tan^{2}x}=\frac{2}{\frac{1-tan^{2}x}{tanx}}$$
$$\frac{2tanx}{1-tan^{2}x}=\frac{2tanx}{1-tan^{2}x}$$
Ejercicio # 12
$$cscx=\frac{secx+cscx}{1+tanx}$$
Solución:
$$cscx=\frac{secx+cscx}{1+tanx}$$
$$cscx=\frac{\frac{1}{cosx}+\frac{1}{senx}}{1+\frac{senx}{cosx}}$$
$$cscx=\frac{\frac{senx+cosx}{cosx\cdot senx}}{\frac{cosx+senx}{cosx}}$$
$$cscx=\frac{cosx}{cosx\cdot senx}$$
$$cscx=\frac{1}{senx}$$
$$cscx=cscx$$
Ejercicio # 13
$$\frac{senx\cdot tanx}{cscx-cotx}-senx=tanx$$
Solución:
$$\frac{senx\cdot tanx}{cscx-cotx}-senx=tanx$$
$$\frac{senx\cdot tanx-senx(cscx-cotx)}{cscx-cotx}=tanx$$
$$\frac{senx(tanx-cscx+cotx)}{cscx-cotx}=tanx$$
$$\frac{senx(tanx+cotx-cscx)}{cscx-cotx}=tanx$$
$$\frac{senx(tanx+\frac{1}{tanx}-cscx)}{cscx-cotx}=tanx$$
$$\frac{senx(\frac{tan^{2}x+1}{tanx}-cscx)}{cscx-cotx}=tanx$$
$$\frac{senx(\frac{tan^{2}x+1-cscxtanx}{tanx})}{cscx-cotx}=tanx$$
$$\frac{senx(\frac{sec^{2}x-secx}{tanx})}{cscx-cotx}=tanx$$
$$\frac{cosx(sec^{2}x-secx)}{\frac{1}{senx}-\frac{cosx}{senx}}=tanx$$
$$\frac{cosx(sec^{2}x-secx)}{\frac{1-cosx}{senx}}=tanx$$
$$\frac{senx\cdot cosx(sec^{2}x-secx)}{1-cosx}=tanx$$
$$\frac{senx\cdot cosx(\frac{1}{cos^{2}x}-\frac{1}{cosx})}{1-cosx}=tanx$$
$$\frac{senx\cdot cosx(\frac{cosx-cos^{2}x}{cos^{3}x})}{1-cosx}=tanx$$
$$\frac{\frac{senx\cdot cosx}{cos^{3}x}(cosx-cos^{2}x)}{1-cosx}=tanx$$
$$\frac{\frac{senx}{cosx\cdot cosx}(cosx-cos^{2}x)}{1-cosx}=tanx$$
$$\frac{tanx\cdot secx[cosx(1-cosx)]}{1-cosx}=tanx$$
$$\frac{tanx\cdot secx\cdot cosx(1-cosx)}{1-cosx}=tanx$$
$$tanx\cdot \frac{1}{cosx}\cdot cosx=tanx$$
$$tanx=tanx$$
Ejercicio # 14
$$(tanx+cotx)\cdot tanx=sec^{2}x$$
Solución:
$$(tanx+cotx)\cdot tanx=sec^{2}x$$
$$tan^{2}x+cot^{2}x\cdot tanx=sec^{2}x$$
$$tan^{2}x+\frac{cosx}{senx}\cdot \frac{senx}{cosx}=sec^{2}x$$
$$tan^{2}x+1=sec^{2}x$$
$$sec^{2}x-1+1=sec^{2}x$$
$$sec^{2}x=sec^{2}x$$
Ejercicio # 15
$$\frac{1}{cscx-cotx}+\frac{1}{cscx+cotx}=2cscx$$
Solución:
$$\frac{1}{cscx-cotx}+\frac{1}{cscx+cotx}=2cscx$$
$$\frac{cscx+cotx+cscx-cotx}{csc^{2}x-cot^{2}x}=2cscx$$
$$\frac{2cscx}{csc^{2}x-cot^{2}x}=2cscx$$
$$\frac{2cscx}{csc^{2}x-(csc^{2}x-1)}=2cscx$$
$$\frac{2cscx}{csc^{2}x-csc^{2}x+1}=2cscx$$
$$2cscx=2cscx$$
Ejercicio # 16
$$\frac{cosx}{1-senx}=secx+tanx$$
Solución:
$$\frac{cosx}{1-senx}=secx+tanx$$
$$\frac{\frac{1}{secx}}{1-\frac{1}{cscx}}=secx+tanx$$
$$\frac{\frac{1}{secx}}{\frac{cscx-1}{cscx}}=secx+tanx$$
$$\frac{cscx}{secx(cscx-1)}=secx+tanx$$
$$\frac{cscx}{secx(\frac{1}{senx}-1)}=secx+tanx$$
$$\frac{cscx}{secx(\frac{1-senx}{senx})}=secx+tanx$$
$$\frac{\frac{1}{senx}}{\frac{secx(1-senx)}{senx}}=secx+tanx$$
$$\frac{senx}{senx\cdot secx(1-senx)}=secx+tanx$$
$$\frac{1}{secx(1-senx)}=secx+tanx$$
$$\frac{1}{secx-secx\cdot senx}=secx+tanx$$
$$\frac{1}{secx-\frac{1}{cosx}\cdot senx}=secx+tanx$$
$$\frac{1}{secx-tanx}=secx+tanx$$
$$\frac{1}{secx-tanx}\cdot \frac{secx+tanx}{secx+tanx}=secx+tanx$$
$$\frac{secx+tanx}{sec^{2}x-tan^{2}x}=secx+tanx$$
$$\frac{secx+tanx}{1+tan^{2}x-tan^{2}x}=secx+tanx$$
$$secx+tanx=secx+tanx$$
Ejercicio # 17
$$tanx+cotx=secx+cscx$$
Solución:
$$tanx+cotx=secx+cscx$$
$$\frac{senx}{cosx}+\frac{cosx}{senx}=secx+cscx$$
$$\frac{sen^{2}x+cos^{2}x}{cosx\cdot senx}=secx+cscx$$
$$\frac{1}{cosx\cdot senx}=secx+cscx$$
$$secx+cscx=secx+cscx$$
Ejercicio # 18
$$sec^{2}x+csc^{2}x=\frac{1}{sen^{2}x\cdot cos^{2}x}$$
Solución:
$$sec^{2}x+csc^{2}x=\frac{1}{sen^{2}x\cdot cos^{2}x}$$
$$\frac{1}{cos^{2}x}+\frac{1}{sen^{2}x}=\frac{1}{sen^{2}x\cdot cos^{2}x}$$
$$\frac{sen^{2}x+cos^{2}x}{cos^{2}x\cdot sen^{2}x}=\frac{1}{sen^{2}x\cdot cos^{2}x}$$
$$\frac{1}{sen^{2}x\cdot cos^{2}x}=\frac{1}{sen^{2}x\cdot cos^{2}x}$$
Ejercicio # 19
$$\sqrt{(1-senx)\cdot (1+senx)}=\frac{1}{secx}$$
Solución:
$$\sqrt{(1-senx)\cdot (1+senx)}=\frac{1}{secx}$$
$$\sqrt{1-sen^{2}x}=\frac{1}{secx}$$
$$cosx=\frac{1}{secx}$$
$$\frac{1}{secx}=\frac{1}{secx}$$
Ejercicio # 20
$$sen^{2}x\cdot cos^{2}x+cos^{4}x=cos^{2}x$$
Solución:
$$sen^{2}x\cdot cos^{2}x+cos^{4}x=cos^{2}x$$
$$(1-cos^{2}x)\cdot cos^{2}x+cos^{4}x=cos^{2}x$$
$$cos^{2}x-cos^{4}x+cos^{4}x=cos^{2}x$$
$$cos^{2}x=cos^{2}x$$
Ejercicio # 21
$$2tanx\cdot secx=\frac{1}{1-senx}-\frac{1}{sen(x)+1}$$
Solución:
$$2tanx\cdot secx=\frac{1}{1-senx}-\frac{1}{sen(x)+1}$$
$$2tanx\cdot secx=\frac{sen(x)+1-(1-senx)}{(1-senx)\cdot (1+senx)}$$
$$2tanx\cdot secx=\frac{senx+1-1+senx}{1-sen^{2}x}$$
$$2tanx\cdot secx=\frac{2senx}{1-sen^{2}x}$$
$$2tanx\cdot secx=\frac{2senx}{1-(1-cos^{2}x)}$$
$$2tanx\cdot secx=\frac{2senx}{1-1+cos^{2}x}$$
$$2tanx\cdot secx=\frac{2senx}{cos^{2}x}$$
$$2tanx\cdot secx=\frac{2senx}{cosx\cdot cosx}$$
$$2tanx\cdot secx=2tanx\cdot secx$$
Ejercicio # 22
$$secx-tanx=\frac{1}{secx+tanx}$$
Solución:
$$secx-tanx=\frac{1}{secx+tanx}$$
$$secx-tanx=\frac{1}{secx+tanx}\cdot \frac{secx-tanx}{secx-tanx}$$
$$secx-tanx=\frac{secx-tanx}{sec^{2}x-tan^{2}x}$$
$$secx-tanx=\frac{secx-tanx}{1+tan^{2}x-tanx}$$
$$secx-tanx=\frac{secx-tanx}{1}$$
$$secx-tanx=secx-tanx$$
Ejercicio # 23
$$\frac{senx}{1-cosx}-cotx=cscx$$
Solución:
$$\frac{senx}{1-cosx}-cotx=cscx$$
$$\frac{senx}{1-cosx}-\frac{cosx}{senx}=cscx$$
$$\frac{sen^{2}x-cosx(1-cosx)}{senx(1-cosx)}=cscx$$
$$\frac{sen^{2}x-cosx+cos^{2}x}{senx(1-cosx)}=cscx$$
$$\frac{1-cos^{2}x-cosx+cos^{2}x}{senx(1-cosx)}=cscx$$
$$\frac{1-cosx}{senx(1-cosx)}=cscx$$
$$\frac{1}{senx}=cscx$$
$$cscx=cscx$$
Ejercicio # 24
$$\frac{senx+cosx}{secx+cscx}=senx\cdot cosx$$
Solución:
$$\frac{senx+cosx}{secx+cscx}=senx\cdot cosx$$
$$\frac{senx+cosx}{\frac{1}{cosx}+\frac{1}{senx}}=senx\cdot cosx$$
$$\frac{senx+cosx}{\frac{senx+cosx}{cosx\cdot senx}}=senx\cdot cosx$$
$$\frac{senx+cosx(senx\cdot cosx)}{senx+cosx}=senx\cdot cosx$$
$$senx\cdot cosx=senx\cdot cosx$$
Ejercicio # 25
$$\frac{1-cosx}{senx}+\frac{senx}{1-cosx}=2cscx$$
Solución:
$$\frac{1-cosx}{senx}+\frac{senx}{1-cosx}=2cscx$$
$$\frac{(1-cosx)^{2}+sen^{2}x}{senx(1-cosx)}=2cscx$$
$$\frac{sen^{2}x+(1-2cosx+cos^{2}x)}{senx(1-cosx)}=2cscx$$
$$\frac{sen^{2}x+1-2cosx+cos^{2}x}{senx(1-cosx)}=2cscx$$
$$\frac{sen^{2}x+cos^{2}x+1-2cosx}{senx(1-cosx)}=2cscx$$
$$\frac{1+1-2cosx}{senx(1-cosx)}=2cscx$$
$$\frac{2-2cosx}{senx(1-cosx)}=2cscx$$
$$\frac{2(1-cosx)}{senx(1-cosx)}=2cscx$$
$$2cscx=2cscx$$
Ejercicio # 26
$$\frac{senx}{cscx}+\frac{cosx}{secx}=1$$
Solución:
$$\frac{senx}{cscx}+\frac{cosx}{secx}=1$$
$$\frac{senx\cdot secx+cosx\cdot cscx}{cscx\cdot secx}=1$$
$$\frac{senx\cdot \frac{1}{cosx}+cosx\cdot \frac{1}{sen}}{cscx\cdot secx}=1$$
$$\frac{\frac{senx}{cosx}+ \frac{cosx}{senx}}{\frac{1}{senx}\cdot \frac{1}{cosx}}=1$$
$$\frac{\frac{sen^{2}x+cos^{2}x}{cosx\cdot senx}}{\frac{1}{senx\cdot cosx}}=1$$
$$\frac{senx\cdot cosx}{cosx\cdot senx}=1$$
$$1=1$$
Ejercicio # 27
$$sec^{2}x+csc^{2}x=sec^{2}x\cdot csc^{2}x$$
Solución:
$$sec^{2}x+csc^{2}x=sec^{2}x\cdot csc^{2}x$$
$$\frac{1}{cos^{2}x}+\frac{1}{sen^{2}x}=sec^{2}x\cdot csc^{2}x$$
$$\frac{sen^{2}x+cos^{2}x}{sen^{2}x\cdot cos^{2}x}=sec^{2}x\cdot csc^{2}x$$
$$\frac{1}{sen^{2}x\cdot cos^{2}x}=sec^{2}x\cdot csc^{2}x$$
$$sec^{2}x\cdot csc^{2}x=sec^{2}x\cdot csc^{2}x$$
Ejercicio # 28
$$tanx+cotx=secx\cdot cscx$$
Solución:
$$tanx+cotx=secx\cdot cscx$$
$$\frac{senx}{cosx}+\frac{cosx}{senx}=secx\cdot cscx$$
$$\frac{sen^{2}x+cos^{2}x}{cosx\cdot senx}=secx\cdot cscx$$
$$\frac{1}{cosx\cdot senx}=secx\cdot cscx$$
$$secx\cdot cscx=secx\cdot cscx$$
Ejercicio # 29
$$(1+cot^{2}x)\cdot sen^{2}x=1$$
Solución:
$$(1+cot^{2}x)\cdot sen^{2}x=1$$
$$(1+(csc^{2}x-1)\cdot sen^{2}x=1$$
$$(1+csc^{2}x-1)\cdot sen^{2}x=1$$
$$csc^{2}x\cdot sen^{2}x=1$$
$$\frac{1}{sen^{2}x}\cdot sen^{2}x=1$$
$$1=1$$
Ejercicio # 30
$$cos^{4}x-sen^{4}x-2cos^{2}x=-1$$
Solución:
$$cos^{4}x-sen^{4}x-2cos^{2}x=-1$$
$$cos^{4}x-\left ( sen^{2}x \right )^{2}-2cos^{2}x=-1$$
$$cos^{4}x-\left ( 1-cos^{2}x \right )^{2}-2cos^{2}x=-1$$
$$cos^{4}x-1+2cos^{2}x-cos^{4}x-2cos^{2}x=-1$$
$$-1=-1$$
Ejercicio # 31
Solución:
$$sen^{3}x\cdot cosx+cos^{3}x\cdot senx=senx\cdot cosx$$
$$senx\cdot cosx=senx\cdot cosx$$
Ejemplo # 32
$$\frac{senx}{1+cosx}+\frac{1+cosx}{senx}=2cscx$$
Solución:
$$\frac{senx}{1+cosx}+\frac{1+cosx}{senx}=2cscx$$
$$\frac{sen^{2}x+(1+cosx)^{2}}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{sen^{2}x+(1+2cosx+cos^{2}x)}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{sen^{2}x+1+2cosx+cos^{2}x}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{sen^{2}x+cos^{2}x+1+2cosx}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{1+1+2cosx}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{2+2cosx}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{2(1+cosx)}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{2}{senx}=2cscx$$
$$2cscx=2cscx$$
Ejercicio # 33
$$\frac{senx}{1+cosx}+\frac{1+cosx}{senx}=2cscx$$
Solución:
$$\frac{senx}{1+cosx}+\frac{1+cosx}{senx}=2cscx$$
$$\frac{sen^{2}x+(1+cosx)^{2}}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{sen^{2}x+(1+2cosx+cos^{2}x)}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{sen^{2}x+1+2cosx+cos^{2}x}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{sen^{2}x+cos^{2}x+1+2cosx}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{1+1+2cosx}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{2+2cosx}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{2(1+cosx)}{(1+cosx)\cdot senx}=2cscx$$
$$\frac{2}{senx}=2cscx$$
$$2cscx=2cscx$$
Ejercicio # 34
$$cotx+\frac{senx}{1+cosx}=cscx$$
Solución:
$$cotx+\frac{senx}{1+cosx}=cscx$$
$$\frac{cosx}{senx}+\frac{senx}{1+cosx}=cscx$$
$$\frac{cosx(1+cosx)+sen^{2}x}{senx(1+cosx)}=cscx$$
$$\frac{cosx+cos^{2}x+sen^{2}x}{senx(1+cosx)}=cscx$$
$$\frac{cosx+1}{senx(1+cosx)}=cscx$$
$$\frac{1}{senx}=cscx$$
$$cscx=cscx$$
Ejercicio # 35
$$\frac{cosx}{1-tanx}+\frac{senx}{1-cotx}=senx+cosx$$
Solución:
$$\frac{cosx}{1-tanx}+\frac{senx}{1-cotx}=senx+cosx$$
$$\frac{cosx}{1-\frac{senx}{cosx}}+\frac{senx}{1-\frac{cosx}{senx}}=senx+cosx$$
$$\frac{cosx}{\frac{cosx-senx}{cosx}}+\frac{senx}{\frac{senx-cosx}{senx}}=senx+cosx$$
$$senx+cosx=senx+cosx$$
¡Queremos saber tu opinión de esta guía de Demostraciones de Identidades Trigonométricas!
¿Cuál de estos 35 ejercicios te pareció más desafiante o te hizo pensar mucho? ¡Comparte tus experiencias, tus soluciones alternativas o cualquier duda que tengas en los comentarios! Tu perspectiva enriquece a toda la comunidad.
¿Quieres practicar más Demostraciones de Identidades Trigonométricas con un tutor?
Podemos preparar una sesión personalizada con ejercicios guiados, resolución paso a paso y seguimiento del progreso.
© LaProfeMatematik · Aprender con amor de Dios y mucha pasión



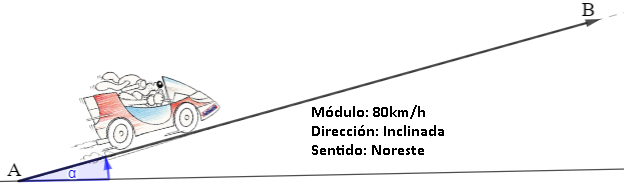
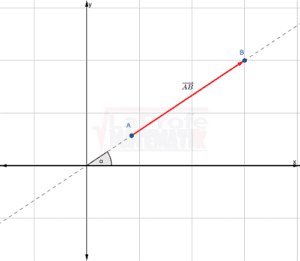
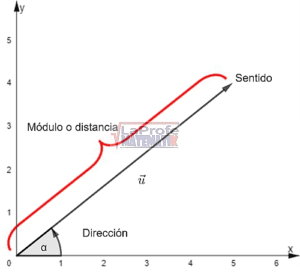
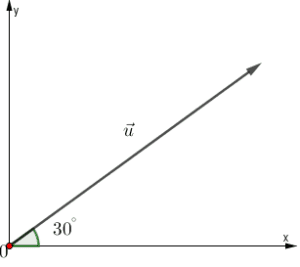
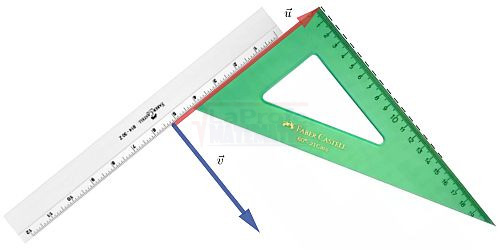
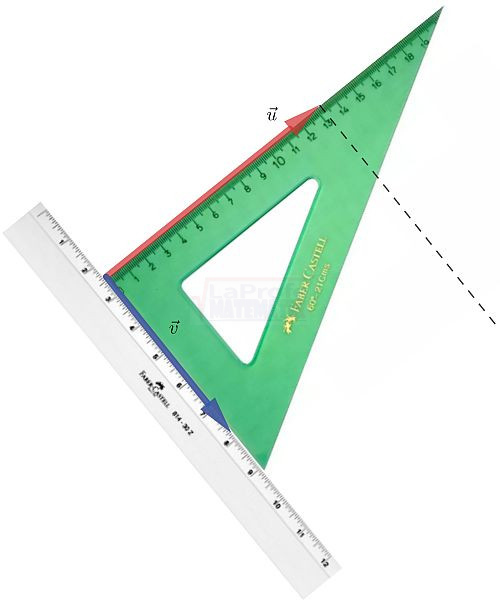
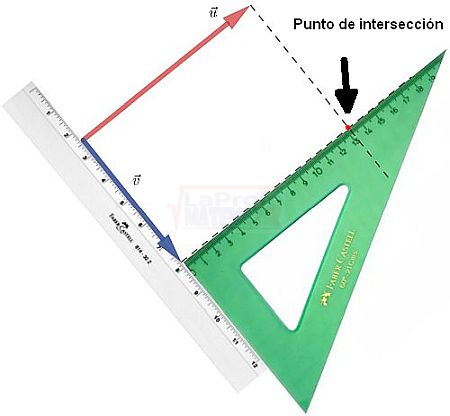
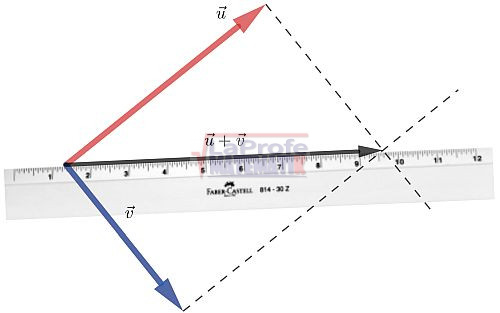
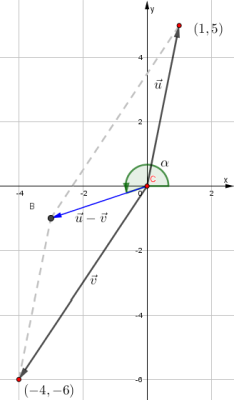
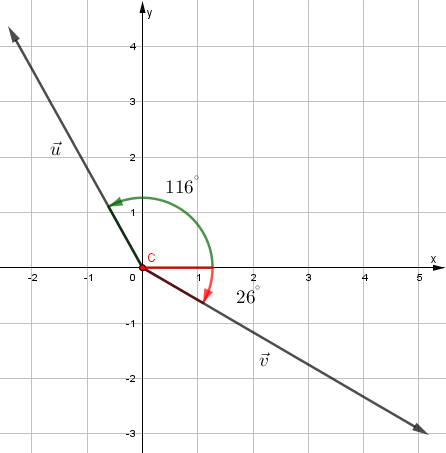
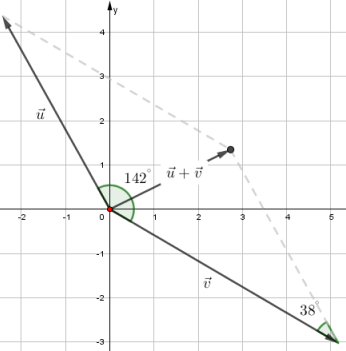
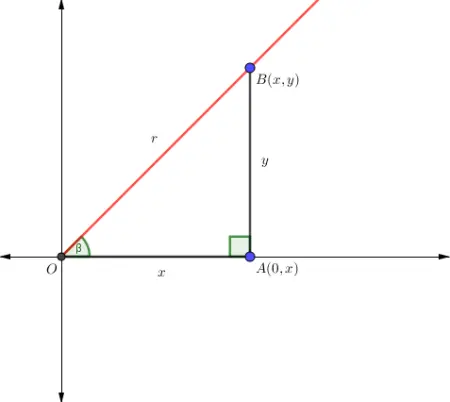
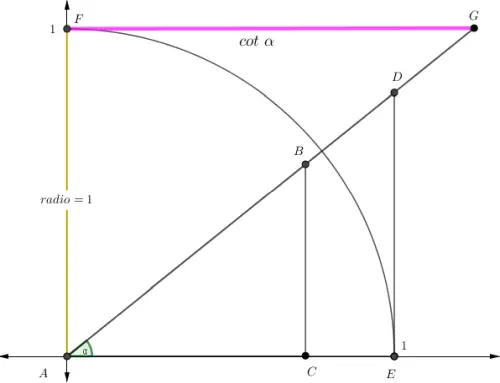
 El ángulo α permite descomponer el vector
El ángulo α permite descomponer el vector 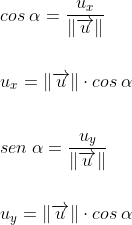





 Solución:
Solución: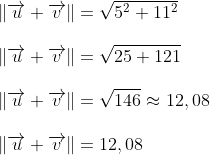
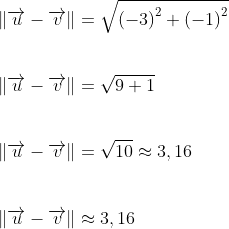
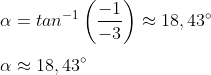
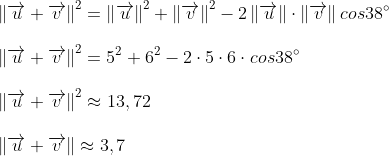


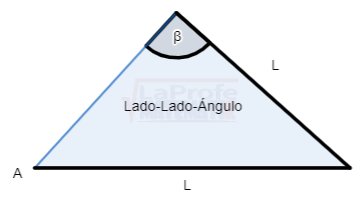
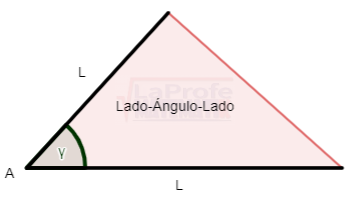
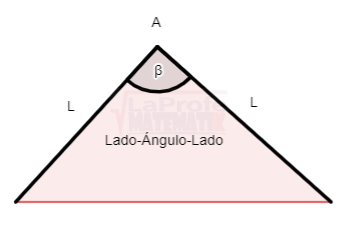
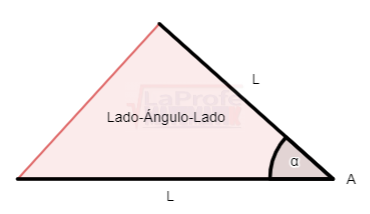
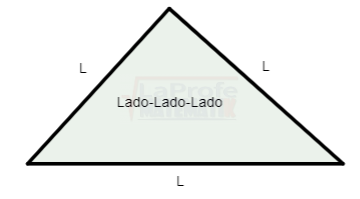
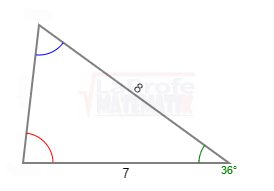
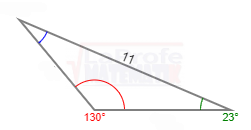
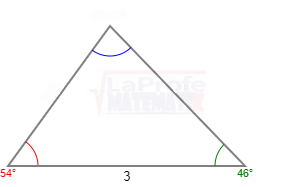
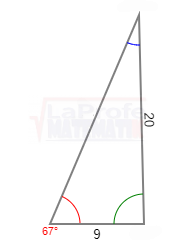
 ¿Sabes qué son los triángulos oblicuángulos y cuáles son las leyes para solucionarlos? Esas leyes se llaman Ley del Seno y Ley del Coseno los dúos dinámicos diseñados para solucionar triángulos oblicuángulos.
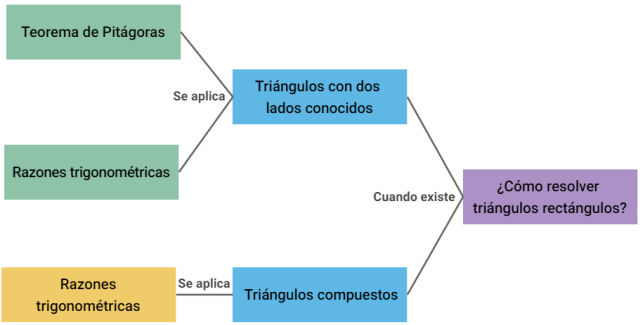
¿Sabes qué son los triángulos oblicuángulos y cuáles son las leyes para solucionarlos? Esas leyes se llaman Ley del Seno y Ley del Coseno los dúos dinámicos diseñados para solucionar triángulos oblicuángulos.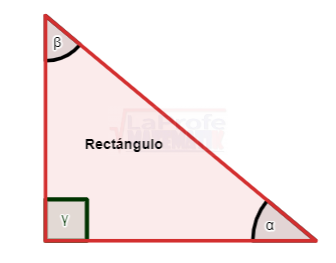 Los triángulos rectángulos se solucionan aplicando tres métodos principales: el teorema de Pitágoras,
Los triángulos rectángulos se solucionan aplicando tres métodos principales: el teorema de Pitágoras, 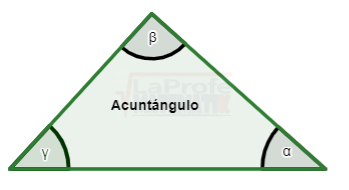
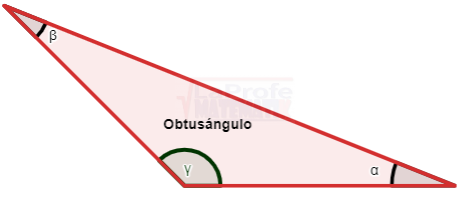
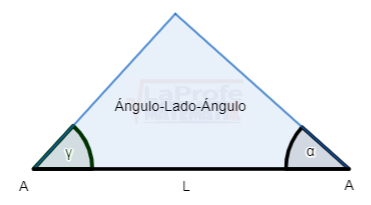
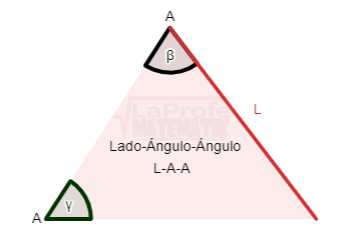
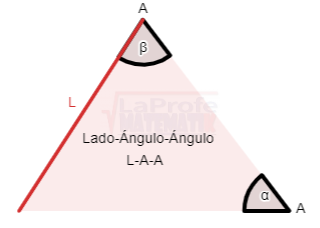
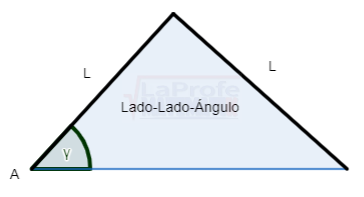

 Ley del coseno
Ley del coseno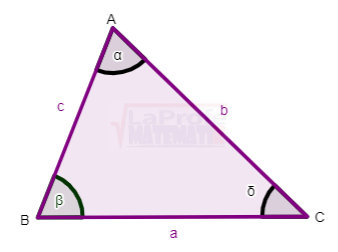

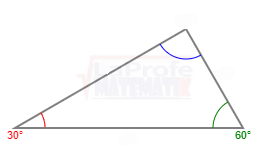
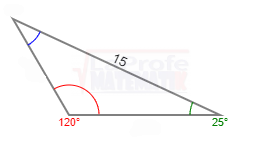
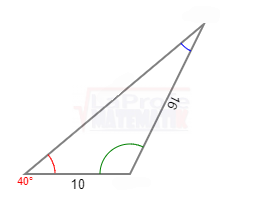
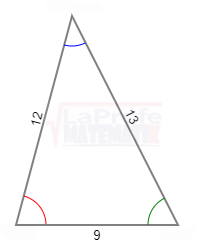


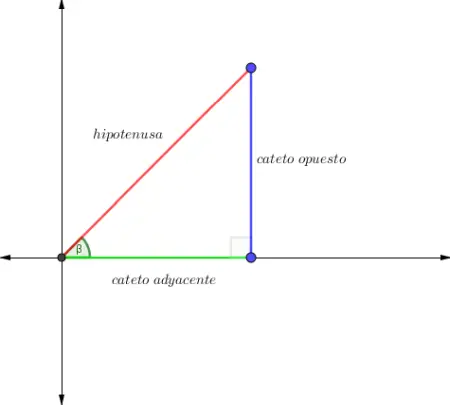
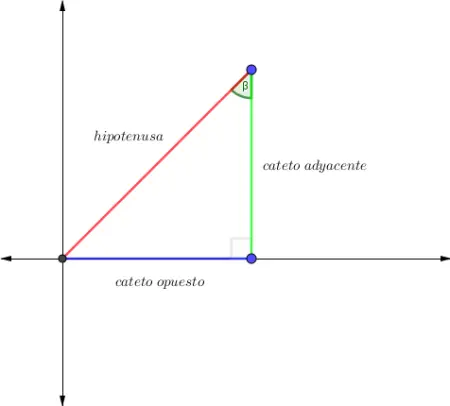
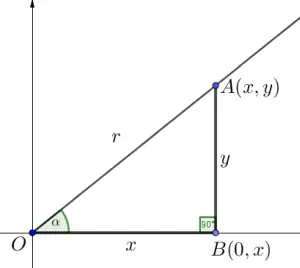
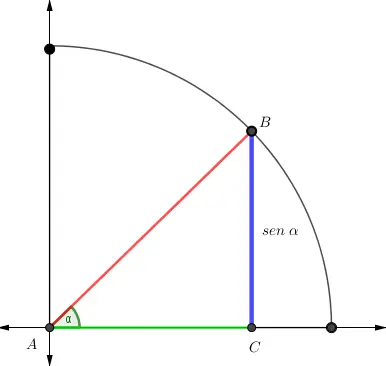
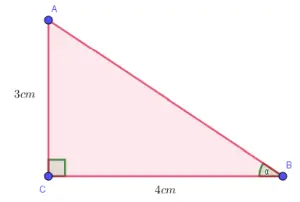
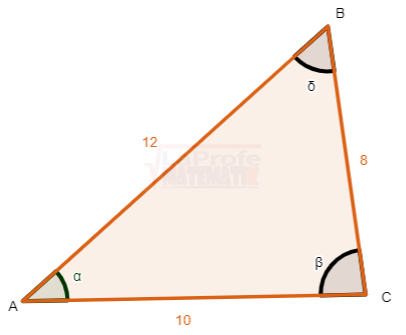
 Los ángulos α y β son complementarios, ya que
Los ángulos α y β son complementarios, ya que 

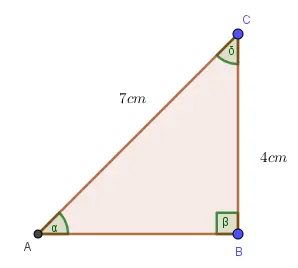



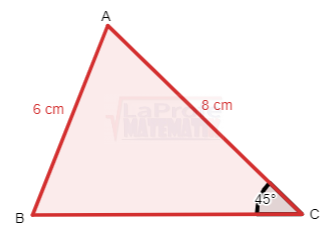
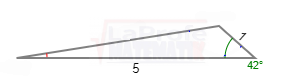
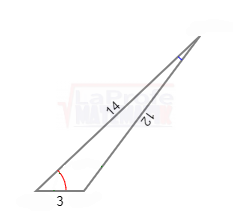
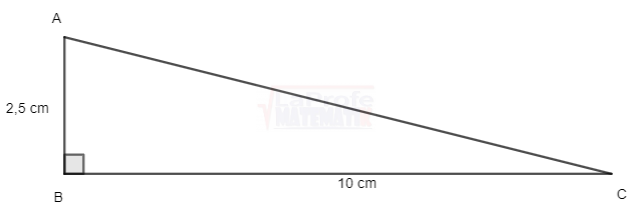 Observa que en el triángulo se desconoce los valores de la hipotenusa y los ángulos del vértice A y C
Observa que en el triángulo se desconoce los valores de la hipotenusa y los ángulos del vértice A y C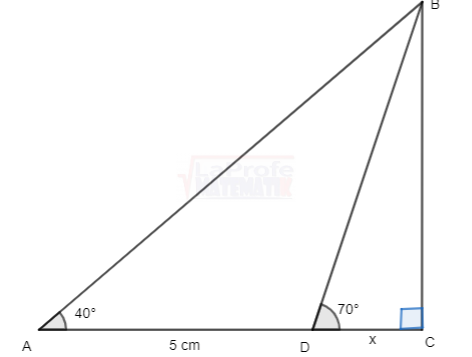 Observa existen tres triángulos, en el triángulo
Observa existen tres triángulos, en el triángulo 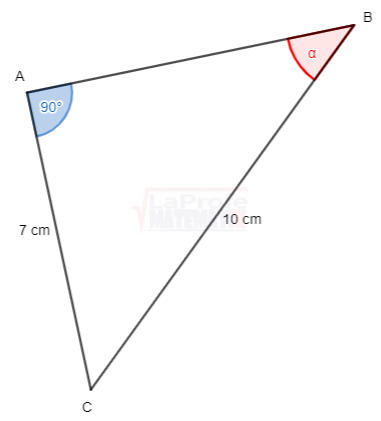
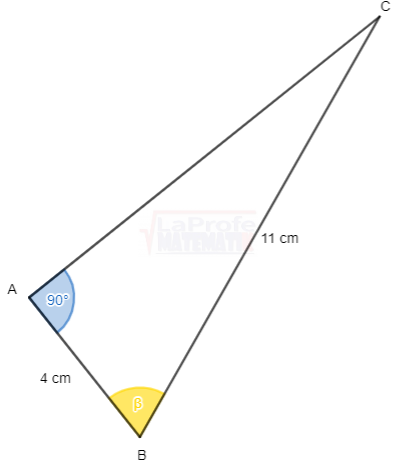

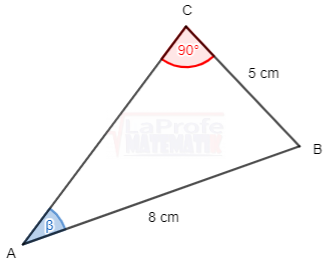
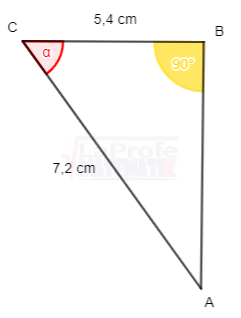
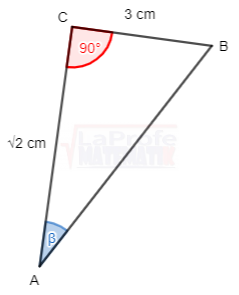
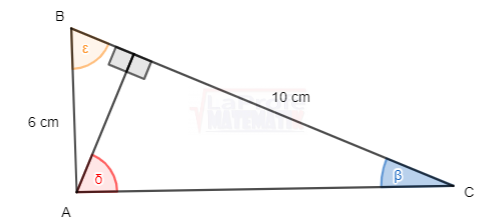

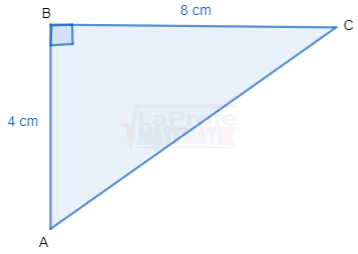
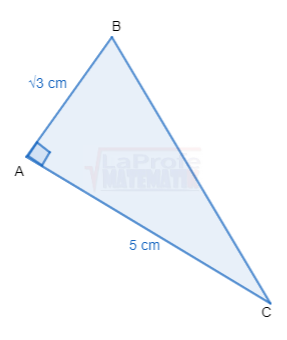

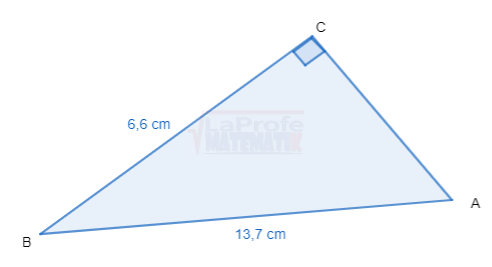
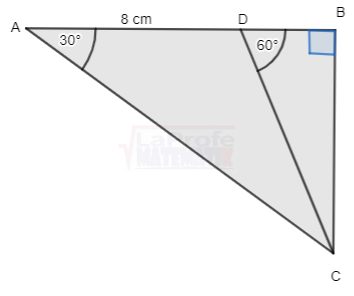
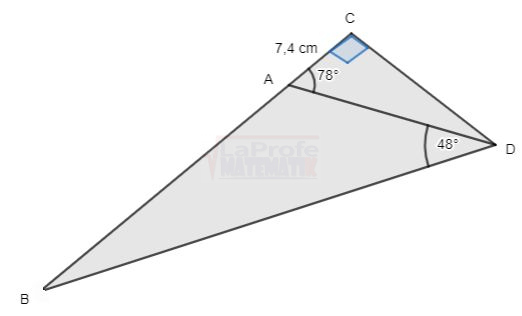
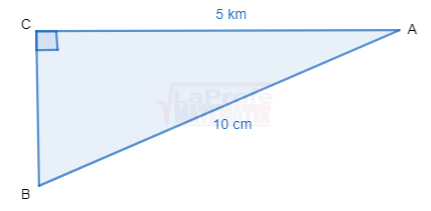 Dibuja cada triángulo rectángulo y resuelve aplicando las razones trigonométricas considerando que a y b son las medidas de los catetos y c la medida de la hipotenusa
Dibuja cada triángulo rectángulo y resuelve aplicando las razones trigonométricas considerando que a y b son las medidas de los catetos y c la medida de la hipotenusa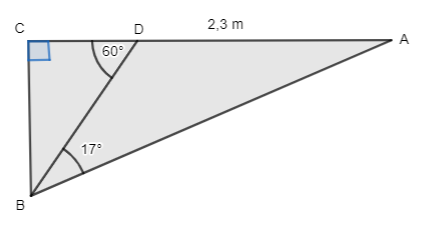
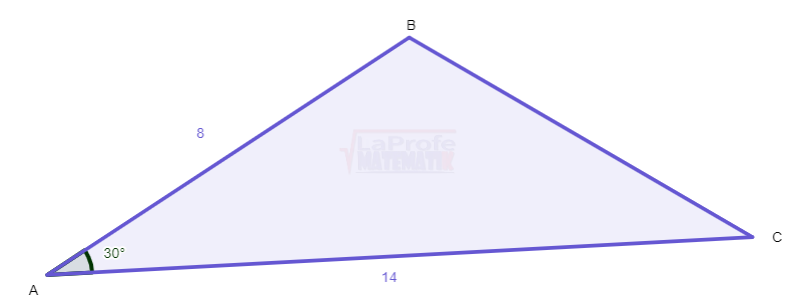
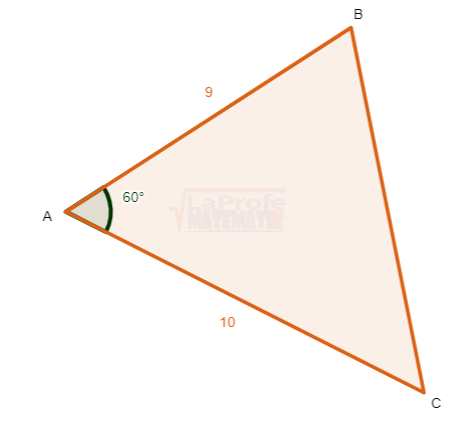
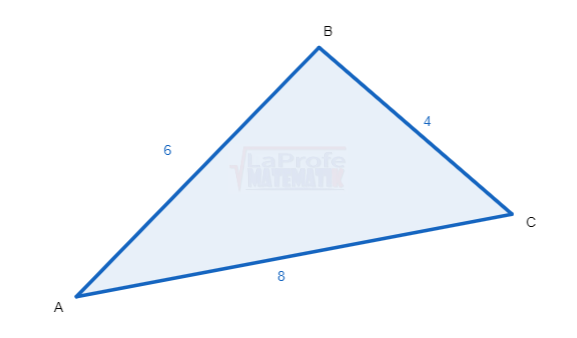

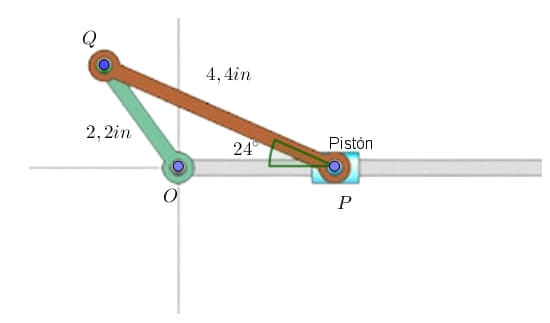
 ¿Alguna vez te has preguntado cómo un robot sabe el ángulo exacto para extender su brazo y recoger un objeto, o cómo tu GPS calcula el ángulo de giro para llevarte a tu destino?
¿Alguna vez te has preguntado cómo un robot sabe el ángulo exacto para extender su brazo y recoger un objeto, o cómo tu GPS calcula el ángulo de giro para llevarte a tu destino? Imagínate una máquina con un avance a la derecha y el otro a la inversa.
Imagínate una máquina con un avance a la derecha y el otro a la inversa.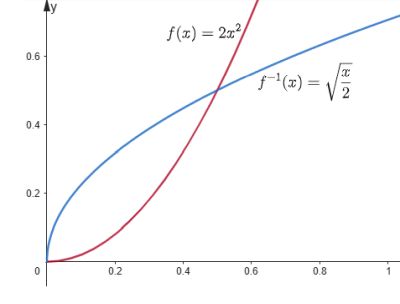
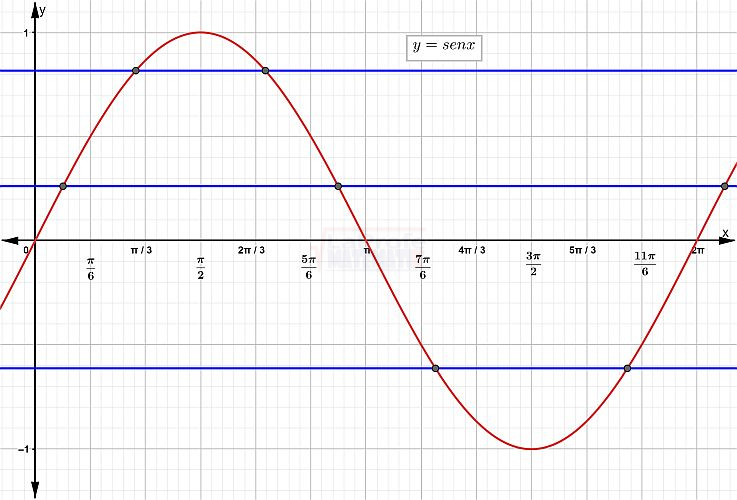
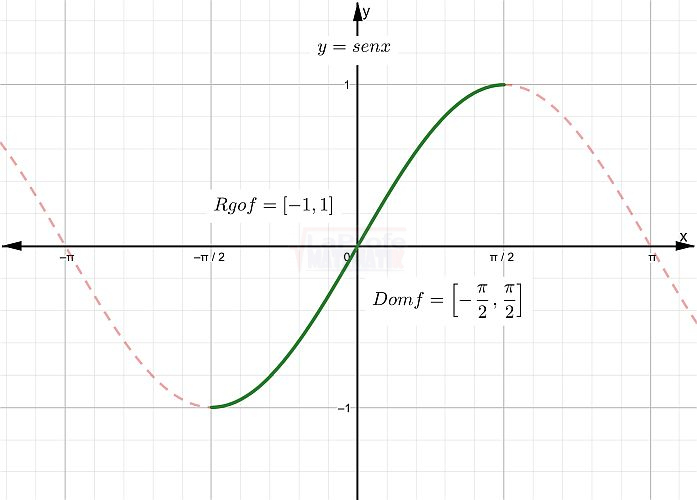
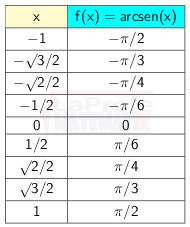 Allí tienes la tabla de valores, te recuerdo que el dominio está comprendido en el intervalo [-1,1]
Allí tienes la tabla de valores, te recuerdo que el dominio está comprendido en el intervalo [-1,1]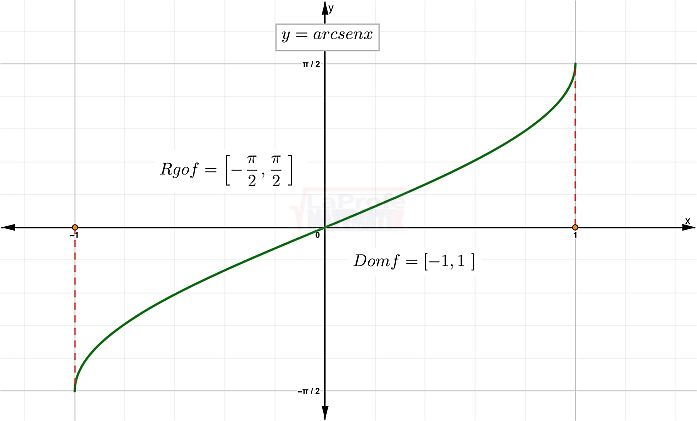
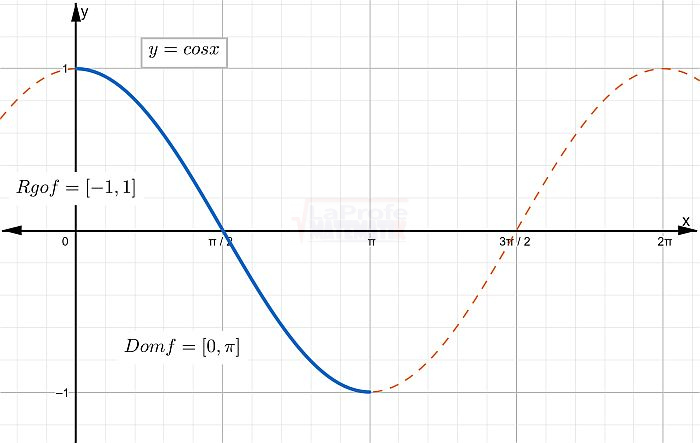
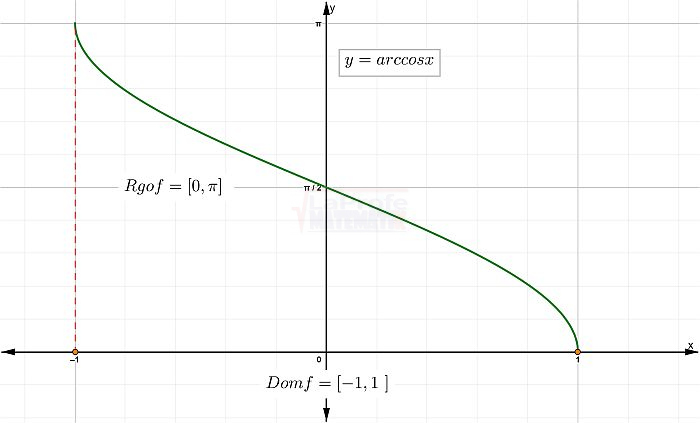
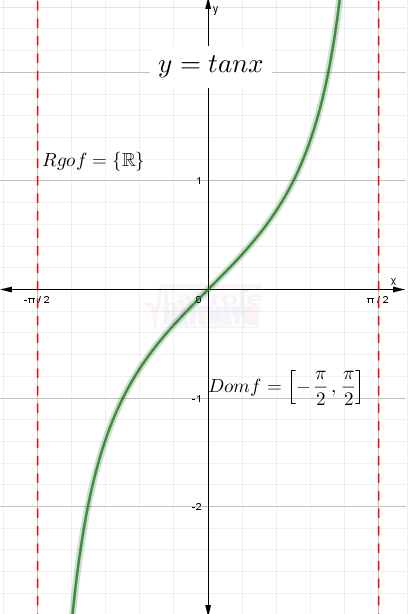
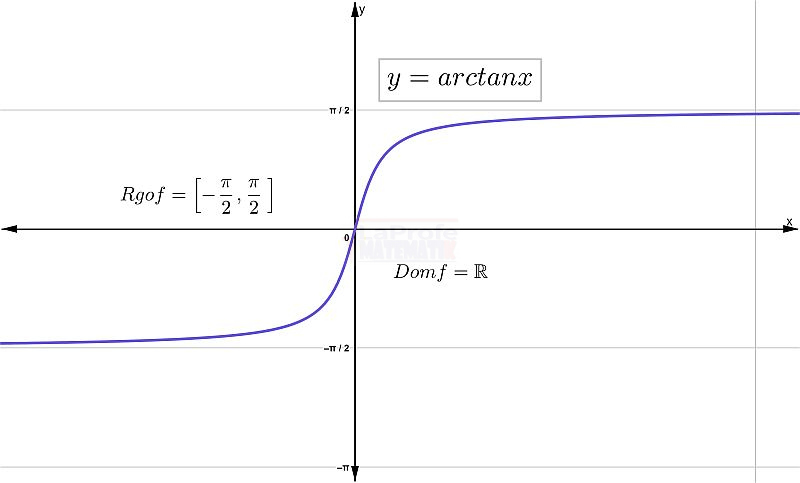
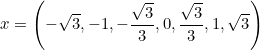
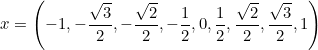
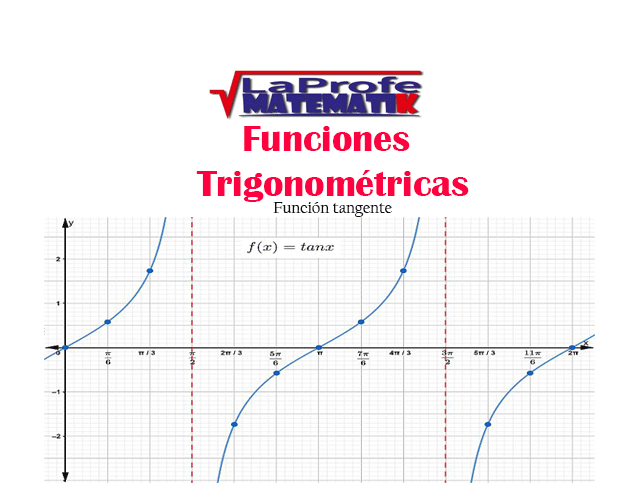
 ¿Sabes qué son las funciones trigonométricas? Considera las matemáticas como una caja de herramientas con la que puedes representar y estudiar cualquier forma o patrón.
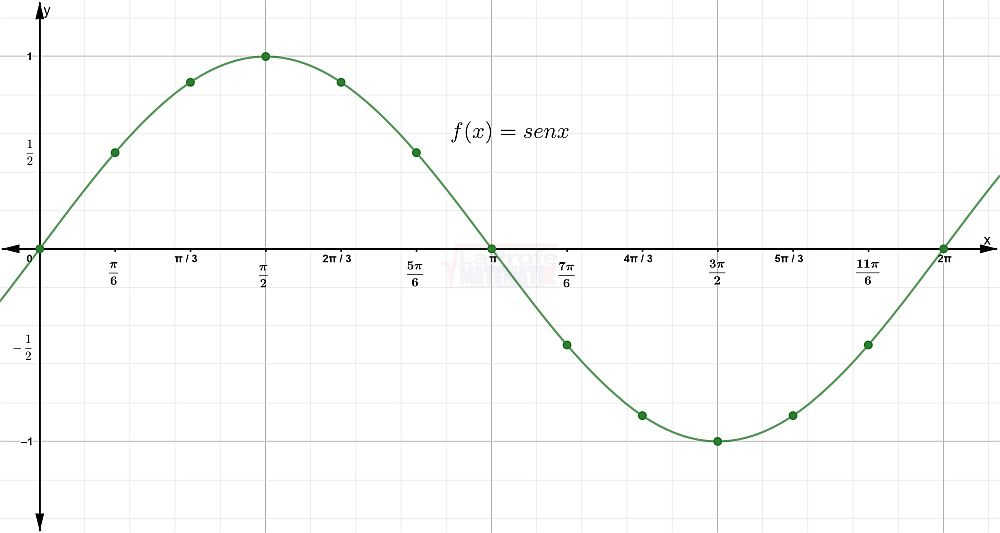
¿Sabes qué son las funciones trigonométricas? Considera las matemáticas como una caja de herramientas con la que puedes representar y estudiar cualquier forma o patrón.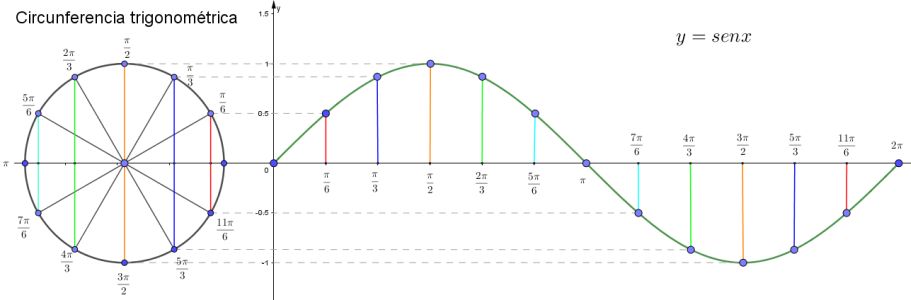
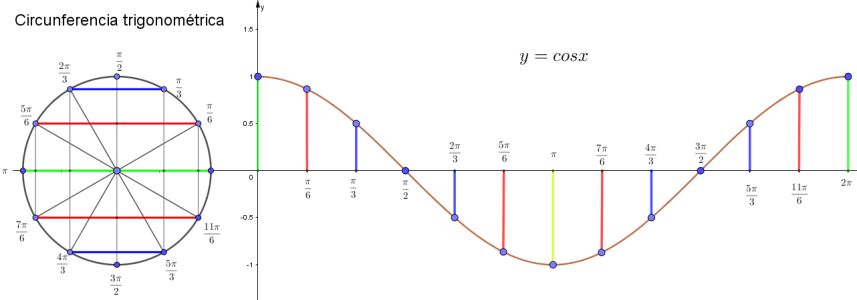
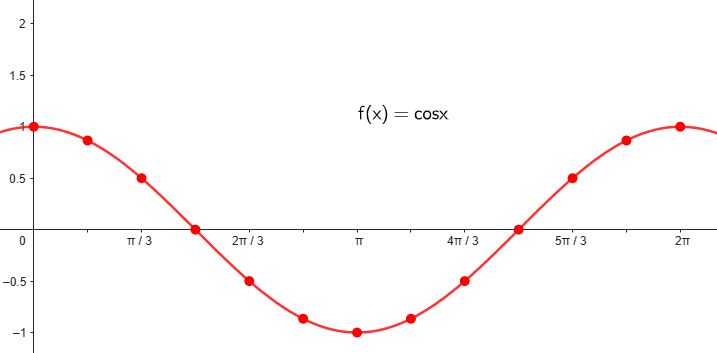
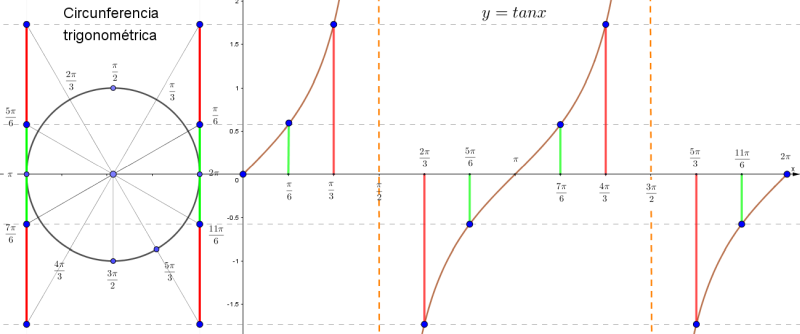
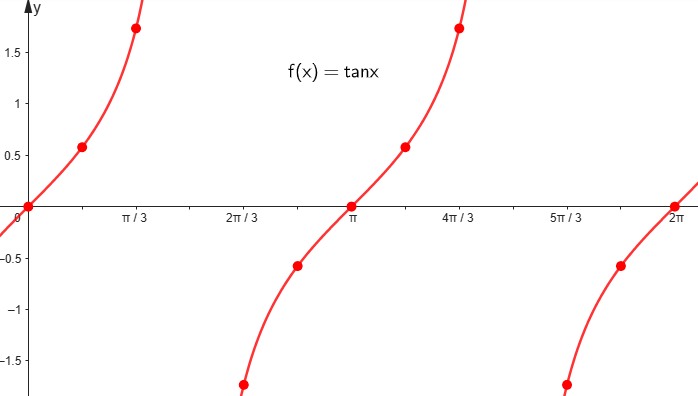
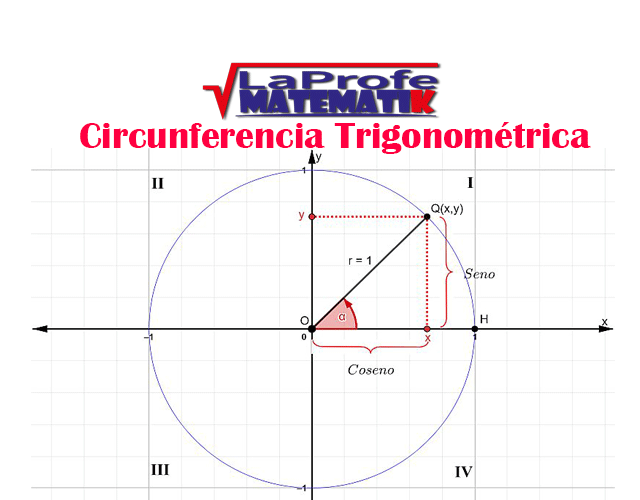
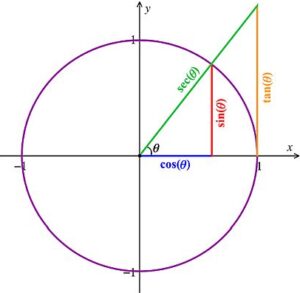
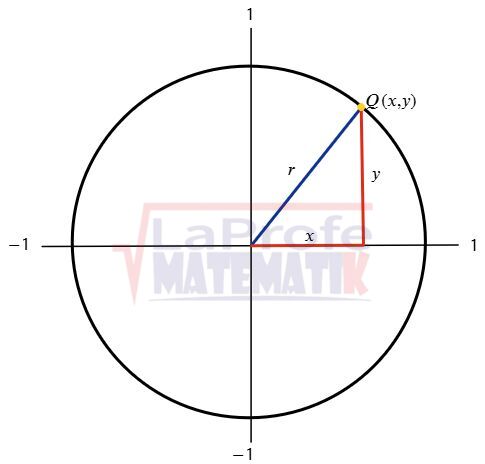
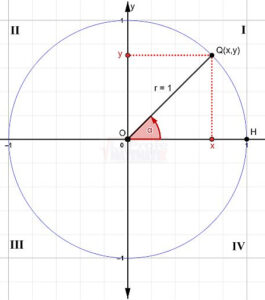
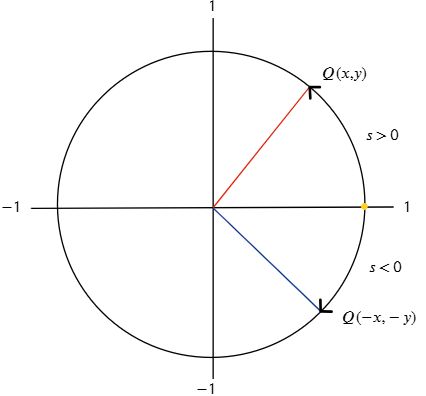
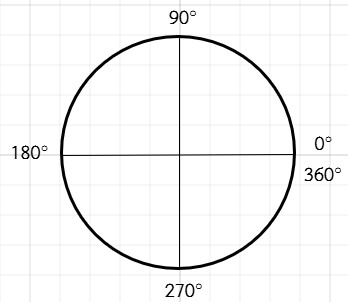
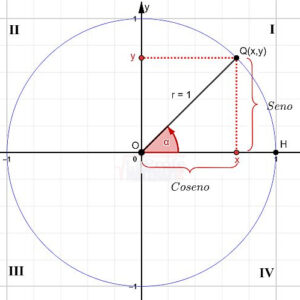
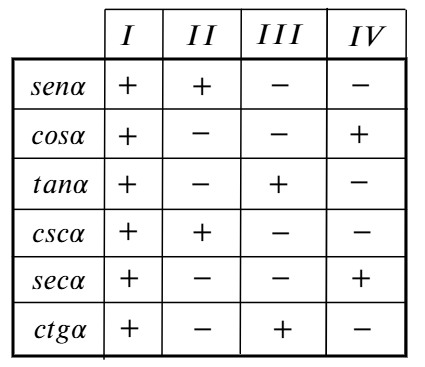
 Explora el simulador de la circunferencia trigonométrica. Desliza el punto rojo y observa cómo cambian los signos de las funciones para cada ángulo. La construcción muestra los lados de un triángulo rectángulo inscrito en la circunferencia, lo que te ayudará a comprender mejor la relación entre ángulos y razones trigonométricas.
Explora el simulador de la circunferencia trigonométrica. Desliza el punto rojo y observa cómo cambian los signos de las funciones para cada ángulo. La construcción muestra los lados de un triángulo rectángulo inscrito en la circunferencia, lo que te ayudará a comprender mejor la relación entre ángulos y razones trigonométricas.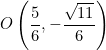
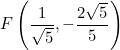
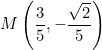
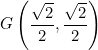
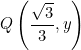 IV cuadrante
IV cuadrante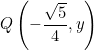 II cuadrante
II cuadrante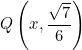 I cuadrante
I cuadrante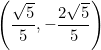
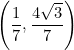
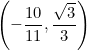
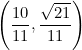
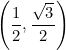
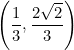
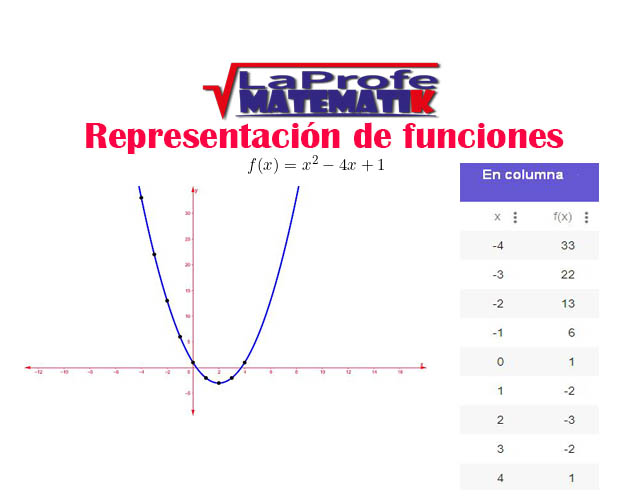
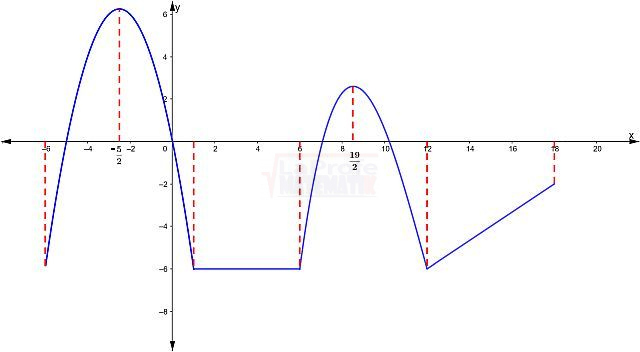
 ¿Has pensado cómo es la representación de funciones en la vida cotidiana? En un juego de fútbol cuando uno de los jugadores patea el balón ¿Qué movimiento describe? y ¿Cómo se puede representar ese movimiento? la representación de datos es muy importante ya que da una observación clara del comportamiento de alguna situación.
¿Has pensado cómo es la representación de funciones en la vida cotidiana? En un juego de fútbol cuando uno de los jugadores patea el balón ¿Qué movimiento describe? y ¿Cómo se puede representar ese movimiento? la representación de datos es muy importante ya que da una observación clara del comportamiento de alguna situación.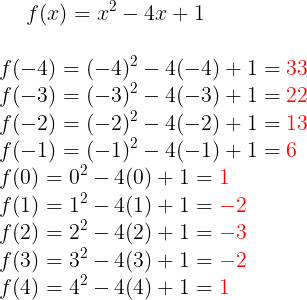
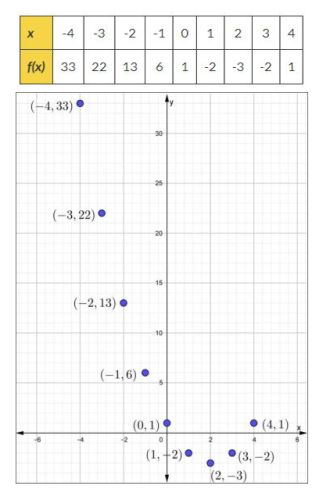
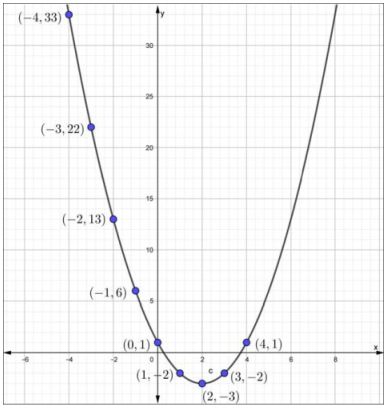
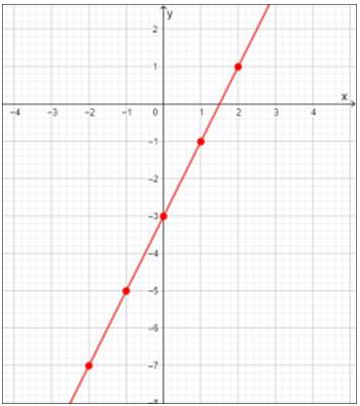
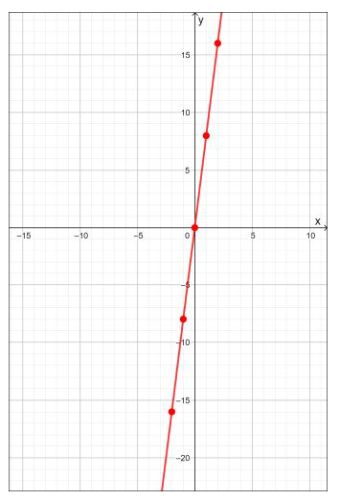
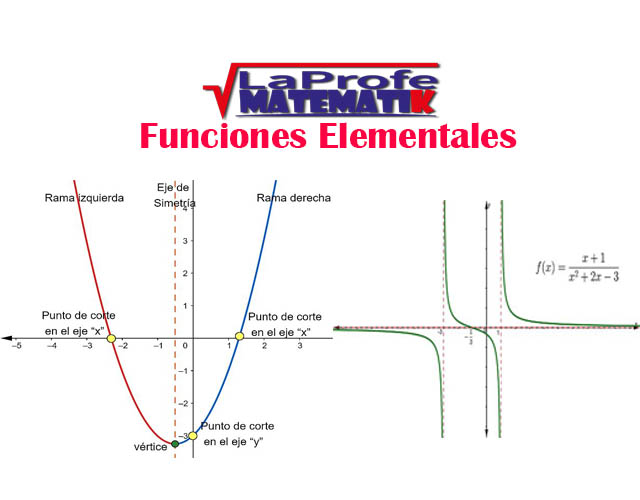

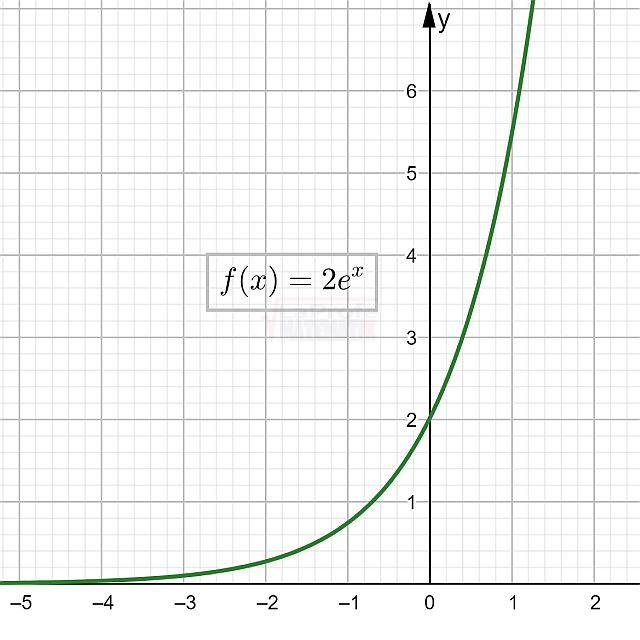
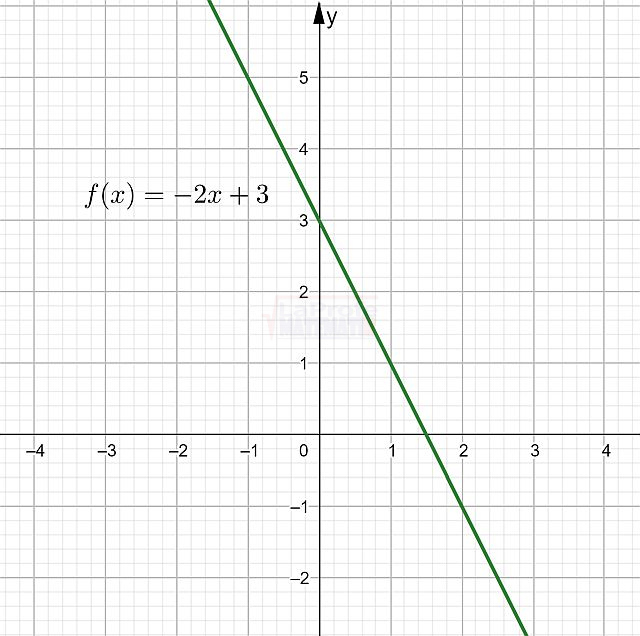
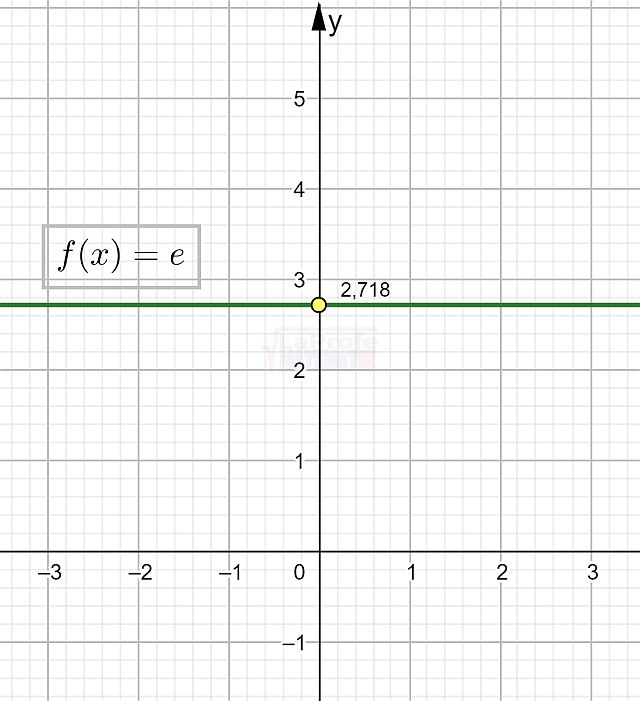
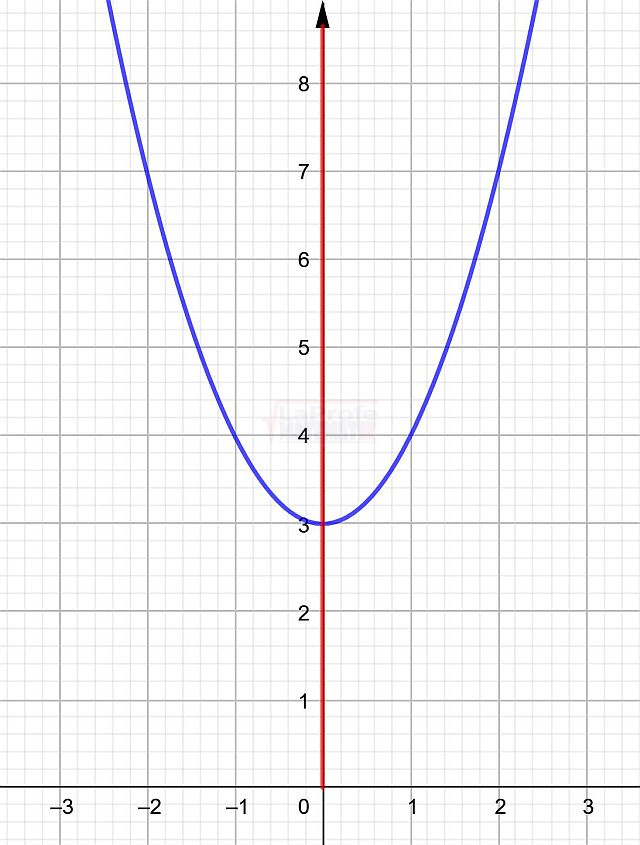
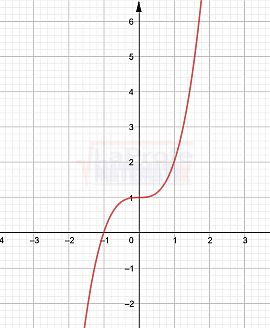
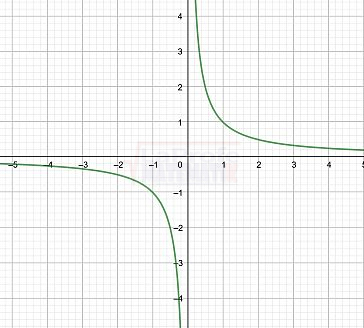
 Las funciones elementales son los bloques de construcción básicos de las matemáticas, ellas son:
Las funciones elementales son los bloques de construcción básicos de las matemáticas, ellas son: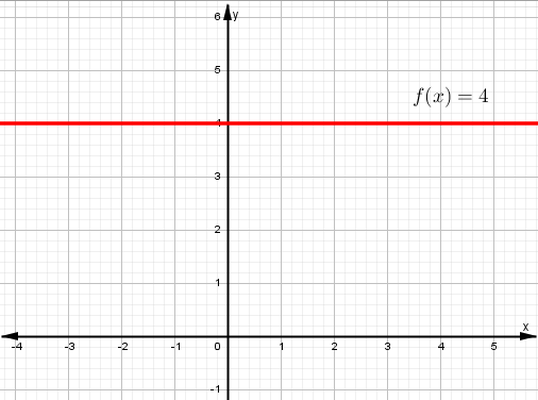
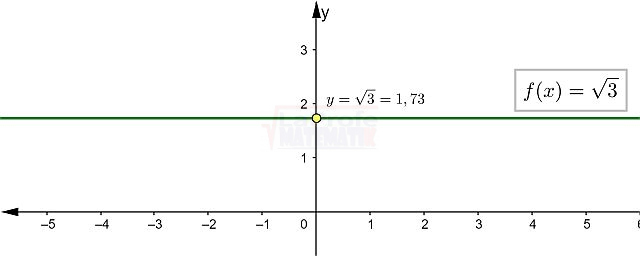
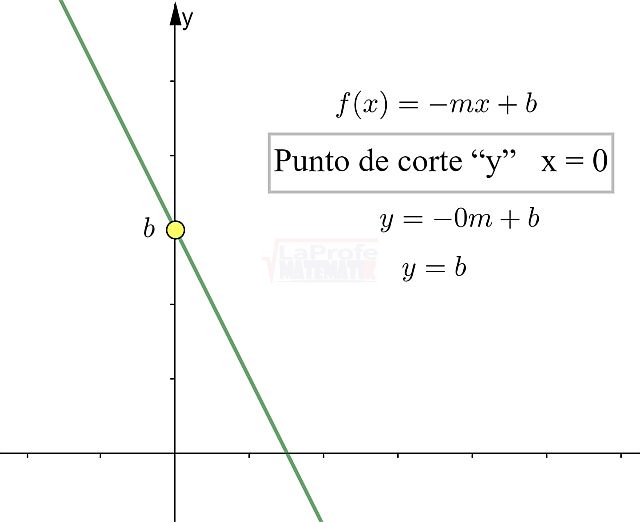
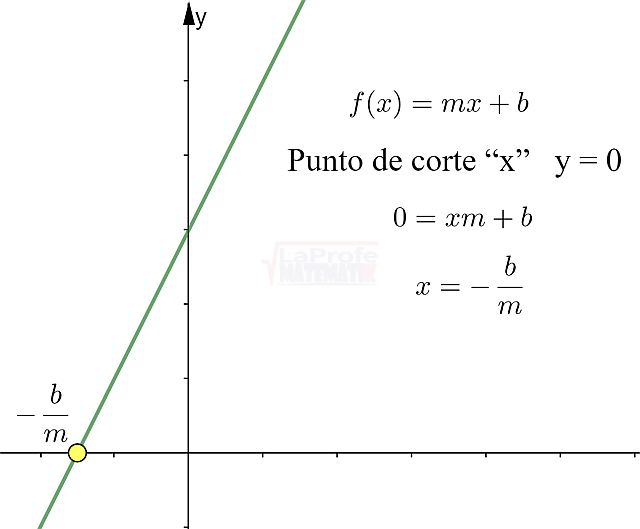
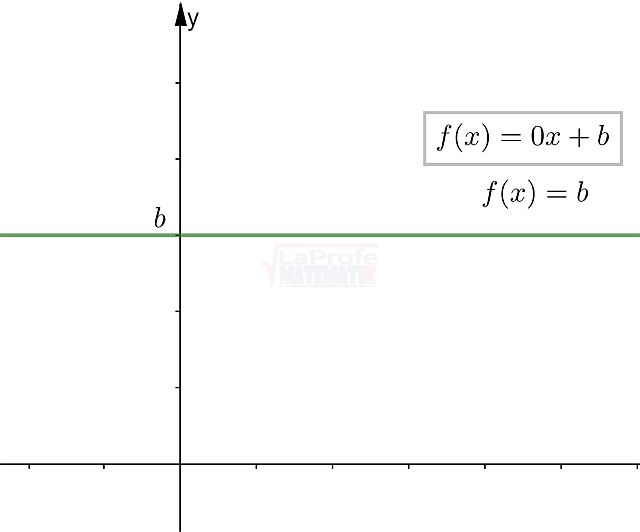
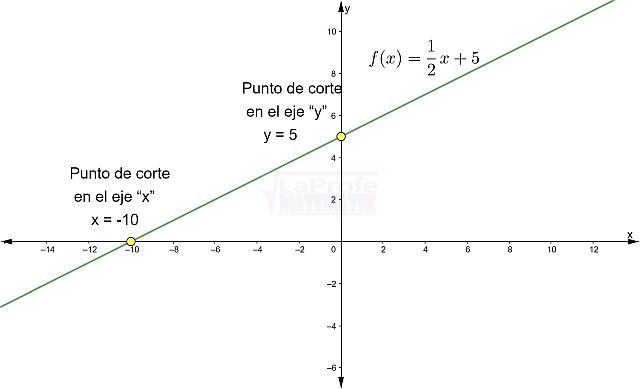


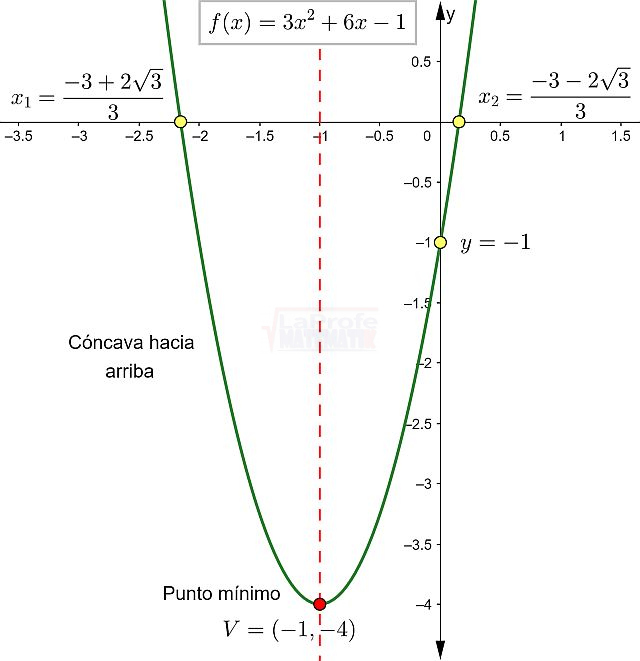

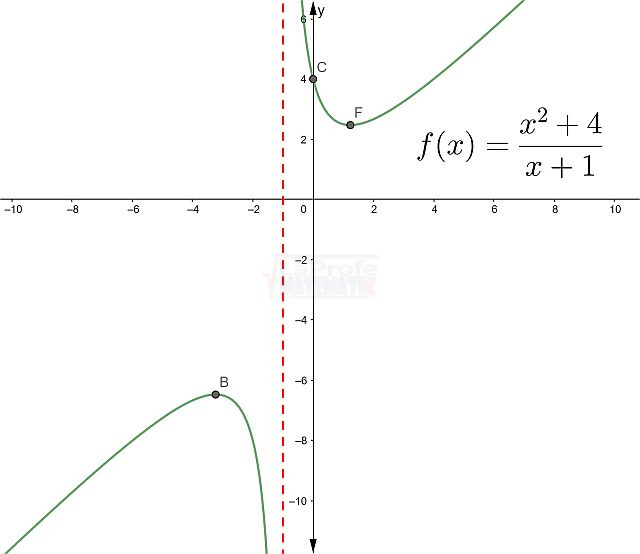
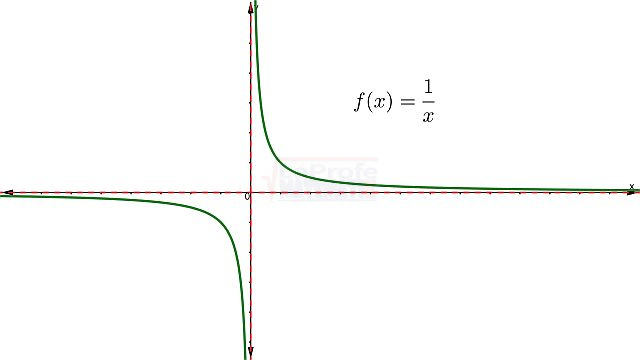
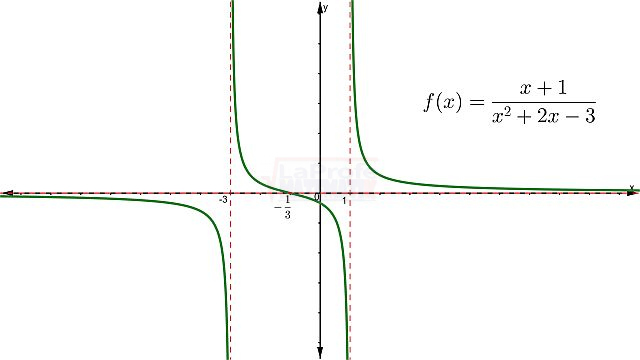
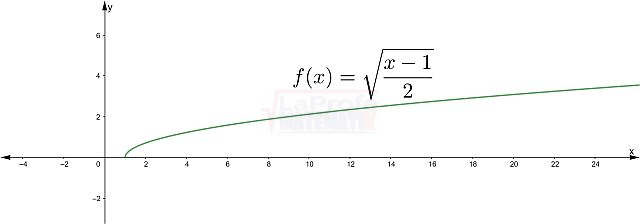


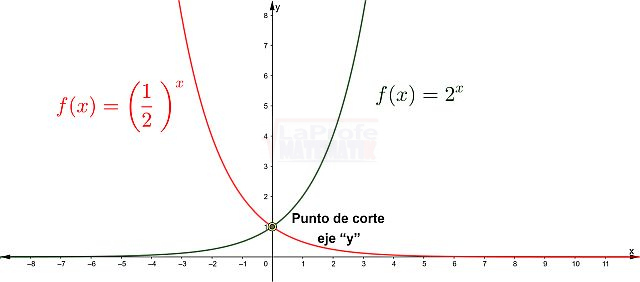
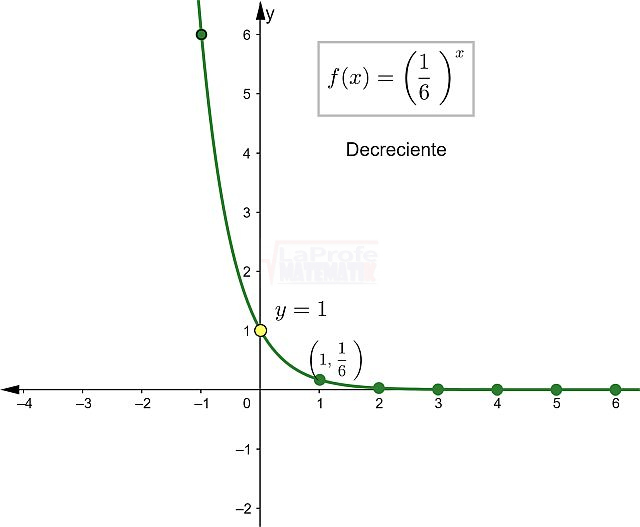
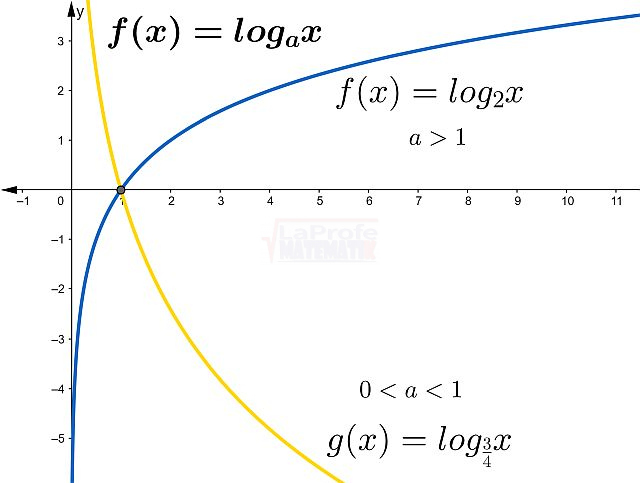
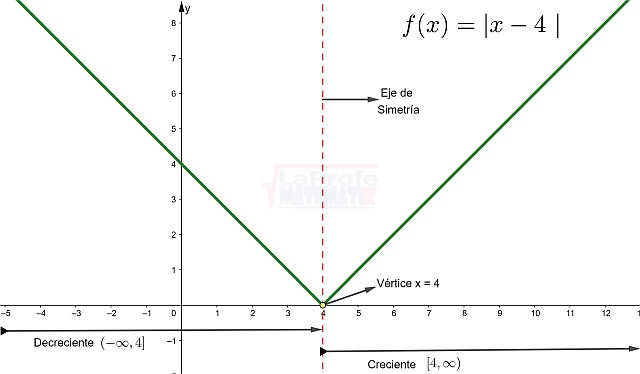
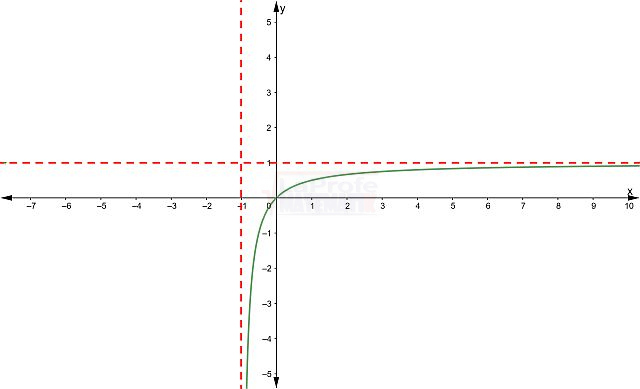
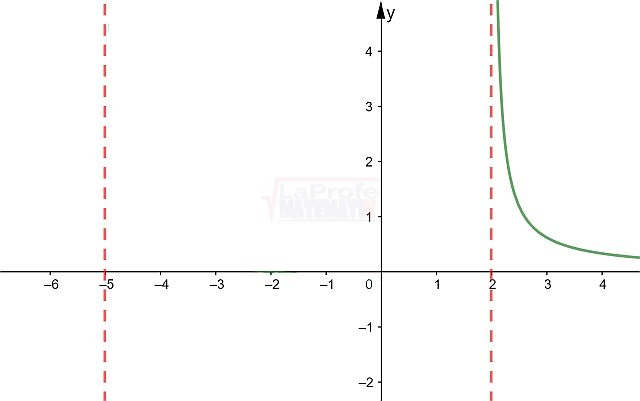
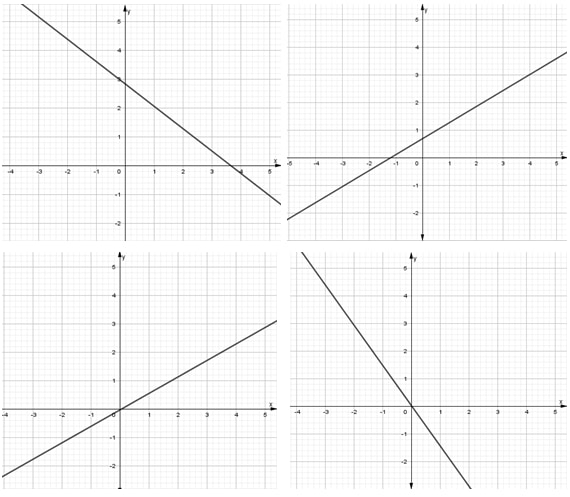
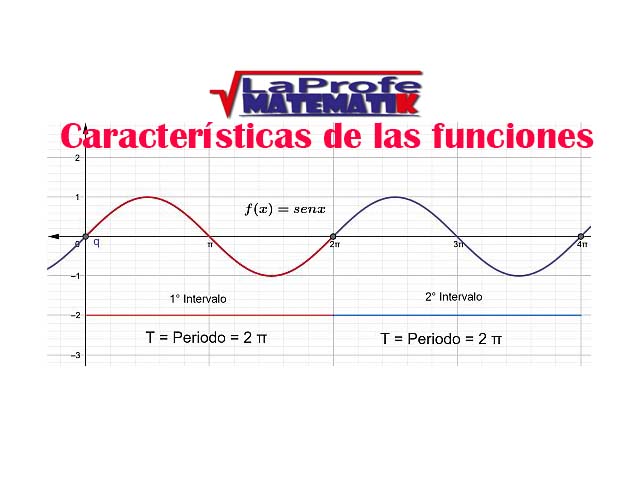
 ¿Sabías que entender las características de las funciones te permite resolver problemas matemáticos de manera mucho más rápida? Al conocer sus propiedades, puedes interpretar su comportamiento y predecir su curva con solo ver su expresión algebraica, sin necesidad de graficar. Esto te da una comprensión profunda de lo que la función representa, agilizando tu estudio analítico y dándote una ventaja para interpretar cualquier expresión matemática.
¿Sabías que entender las características de las funciones te permite resolver problemas matemáticos de manera mucho más rápida? Al conocer sus propiedades, puedes interpretar su comportamiento y predecir su curva con solo ver su expresión algebraica, sin necesidad de graficar. Esto te da una comprensión profunda de lo que la función representa, agilizando tu estudio analítico y dándote una ventaja para interpretar cualquier expresión matemática.